Which Data Structure is used for Implementing Recursion?

Takeaways:

• Meaning of the term “Recursion”.
• Recursion has two components: base case and recurrence relation.
• Stack data structure is used for implementing the recursion.

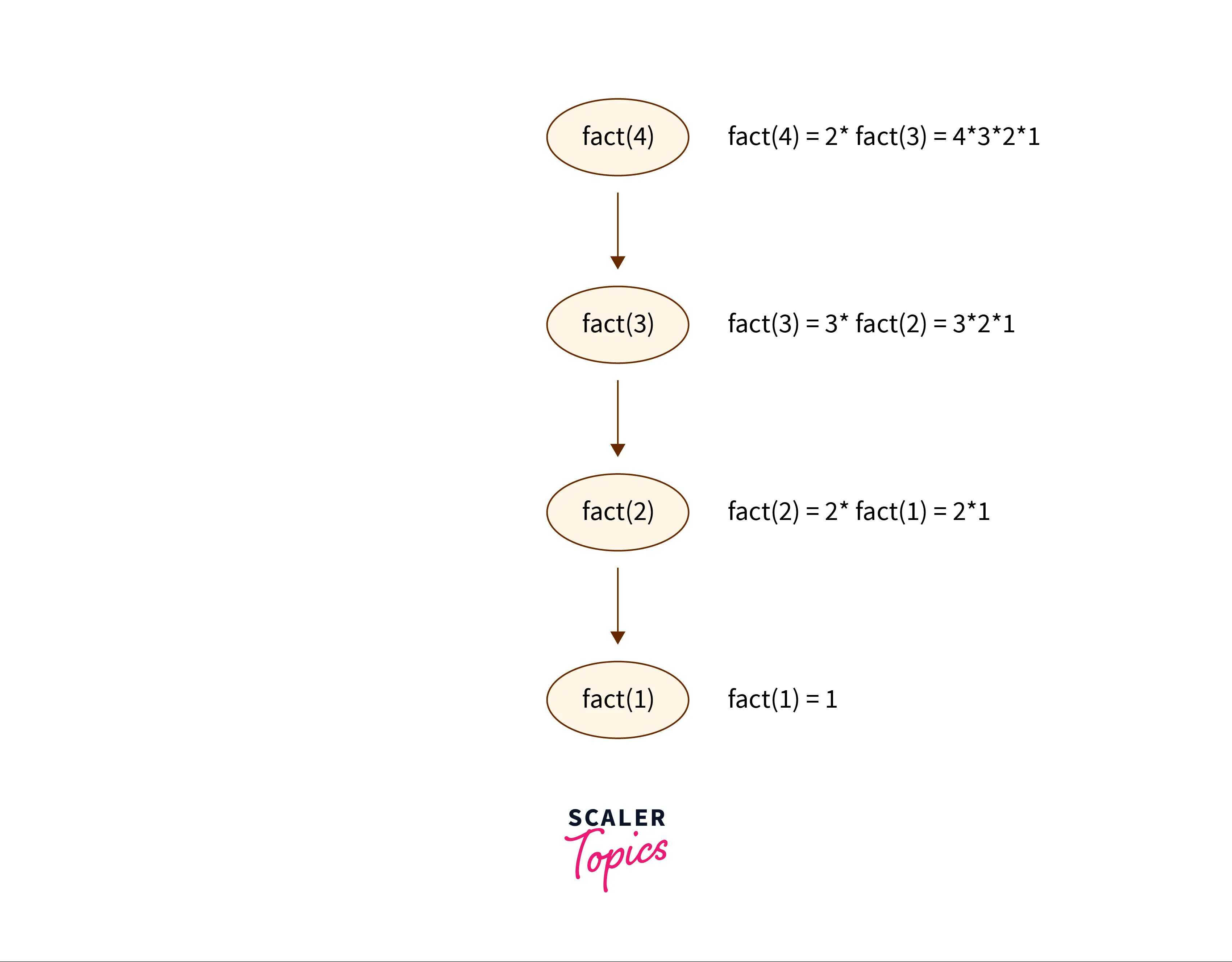
Recursion: Recursion is a technique of problem-solving where a function is called again and again on smaller inputs until some base case i.e. smallest input which has a trivial solution arrives and then we start calculating the solution from that point. Recursion has two parts i.e. first is the base condition and another is the recurrence relation. Let’s understand them one by one using an example of the factorial of a number.

Recurrence: Recurrence is the actual relationship between the same function on different sizes of inputs i.e. we generally compute the solution of larger input using smaller input. For example calculating the factorial of a number, in this problem let’s say we need to calculate the factorial of a number N and we create a helper function say fact(N) which returns the factorial of a number N now we can see that the factorial of a number N using this function can also be represented as

fact(N) = N * fact(N-1)

The function fact(N) calls itself but with a smaller input the above equation is called recurrence relation.

Base condition: This is the condition where the input size given to the input is so small that the solution is very trivial to it. in the case of the above factorial problem we can see that the base condition is fact(1) i.e. on the input N=1 we know the solution is 1.

Recursion backtracks to previous input once it finds the base case and the temporary function calls which are pending are stored in the stack data structure in the memory as follows.

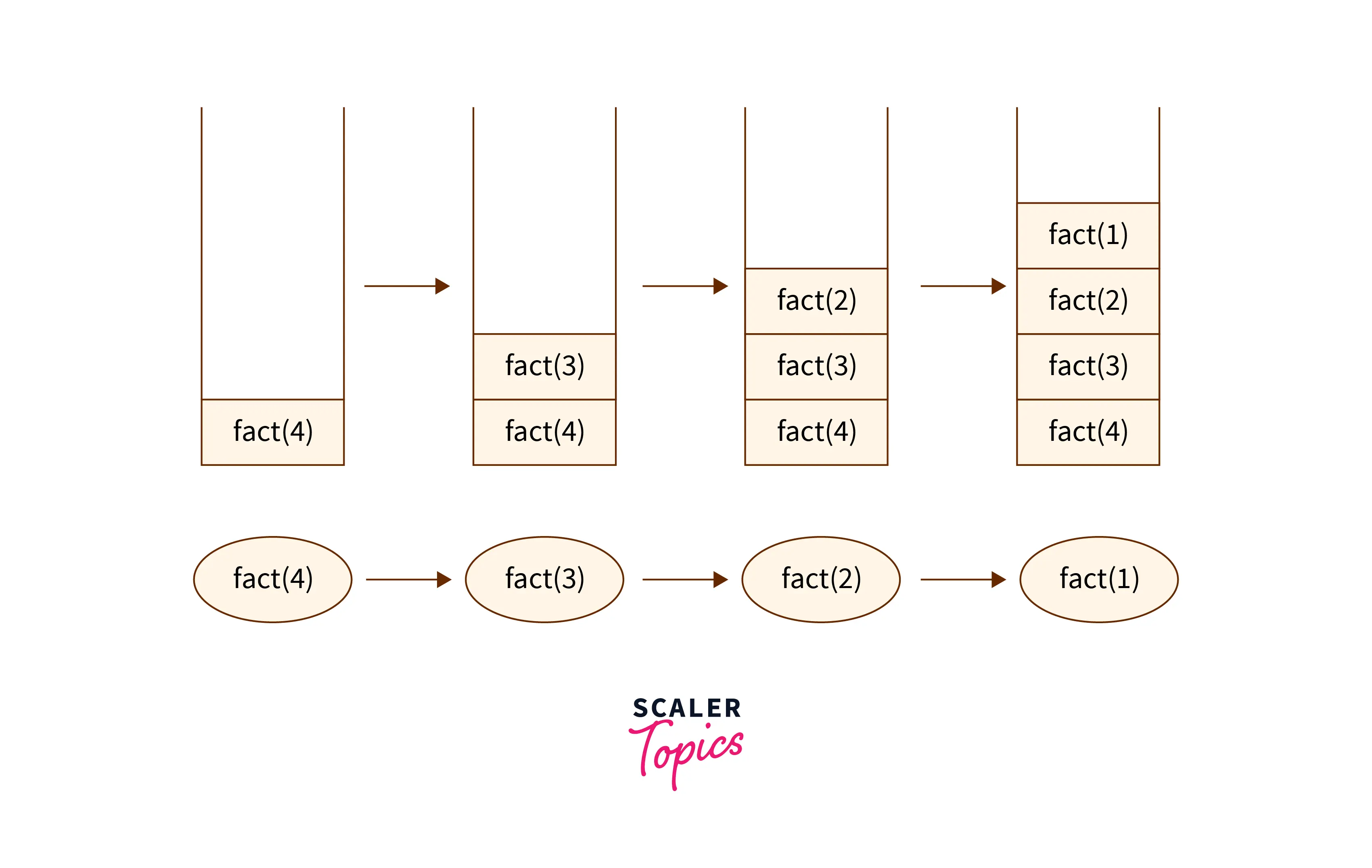
with each function call, the stack keeps filling until the base case arrives which is fact(1) = 1 in this case. After that, each function call is evaluated in the last in first out order.

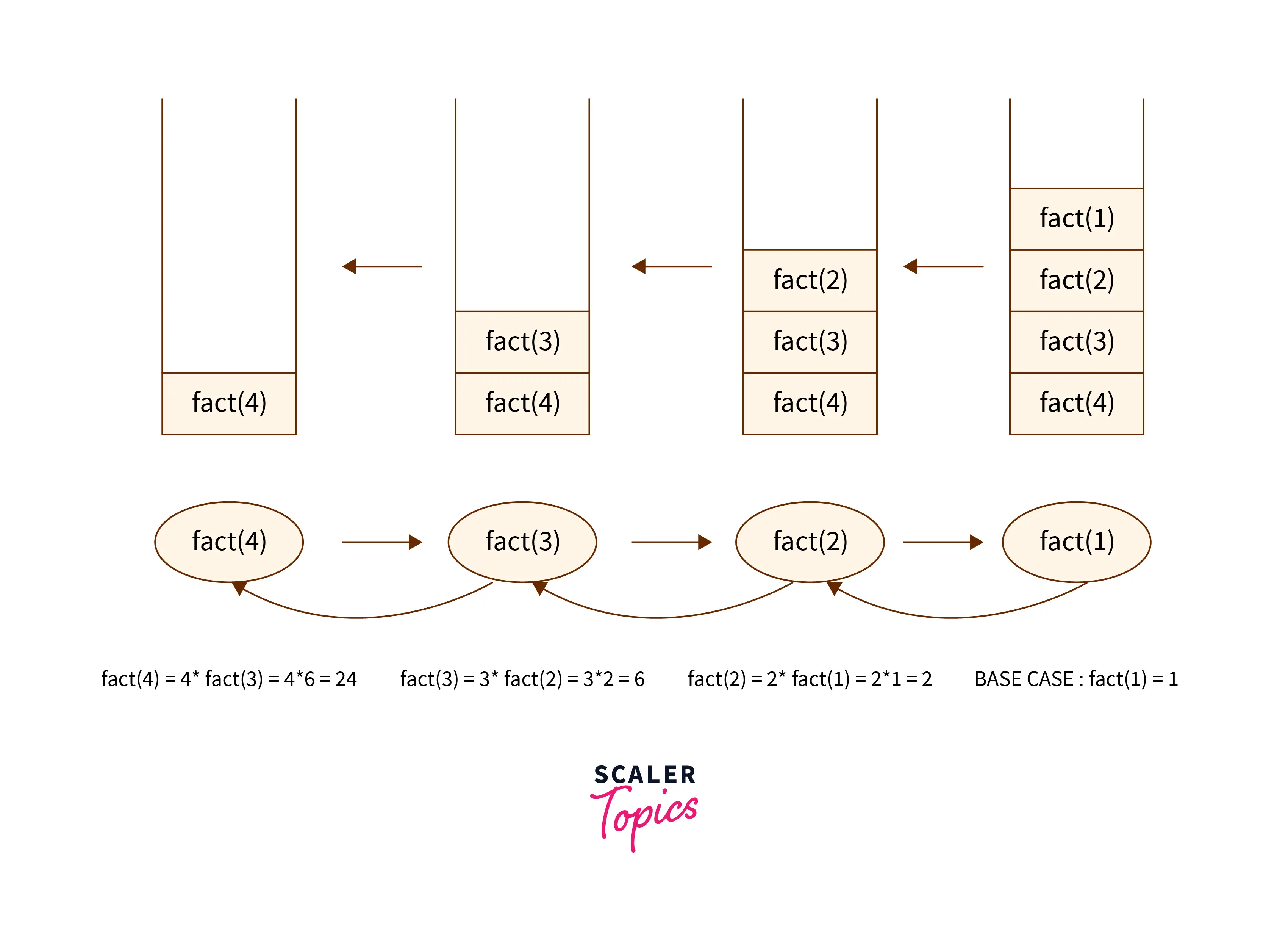
We will discuss the function calls in recursion and consumption of stack in detail.

Implementation Of Recursion

Highlights:

• Recursion is implemented using stack because activation records are to be stored in LIFO order i.e. last in first out.
• An activation record of a function call contains three parts: first is arguments, return address and local variables of the function.

Let’s understand how recursion is implemented, we know that in recursion a function keeps calling itself until the base case arrives after which it backtracks to previous function calls and calculates the output for them now the question is that where are those functions calls stored in memory where the order of function calls must be LIFO i.e. last in first out because we need to solve the recently called function to solve the prior one.

Since we need to keep dividing the given problem to smaller problem until the solution of the problem becomes too naive and eventually backtracking to the previous problem states which are solved with the help of the solution of the smaller problem we need to store those problems in a data structure where we can retrieve those items in a LIFO order i.e. last in first out order and the stack data structure is the most suitable data structure which can be used to implement recursion, some of the high-level programming languages such as C, pascal provide such a stack for bookkeeping.

Let’s understand what are the parameters which are to be stored in the stack when a function is called.

1. First, we need to store the current values of formal parameters i.e. values passed to the function arguments.
2. We also need to store the values of the local variables of the function.
3. Finally, we need to store the return address i.e. address of the function called this procedure or the address where the control has to return after this call i.e one function call is waiting for the another function call to come back.

The three records above are combined called activation records as shown in the image below:

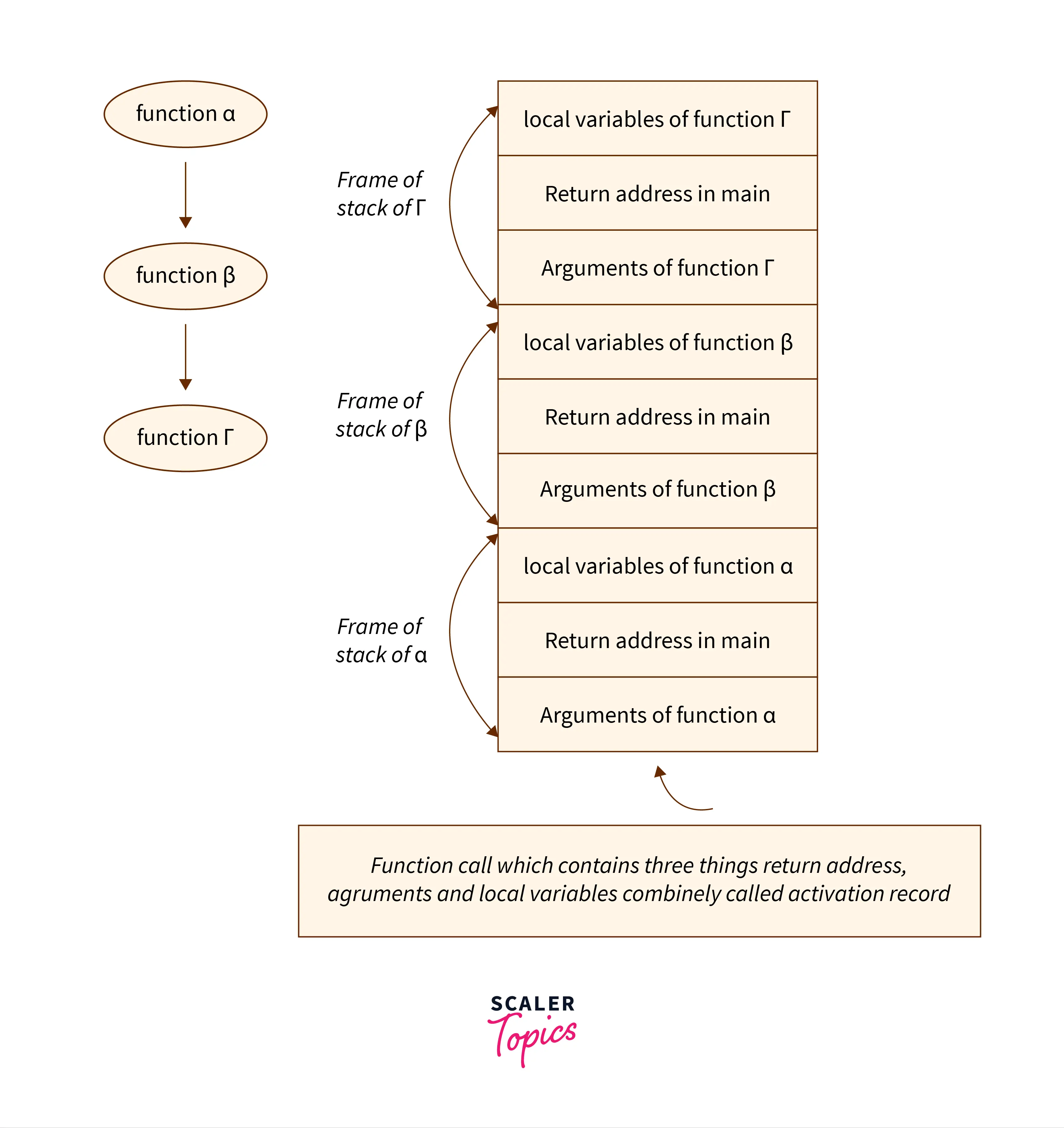
A single activation record contains arguments of the function, return address i.e. address of the calling function, and local variable values and the stack maintains such activation records for each function call.

Let’s take an example of dfs on a tree, the problem is that given a tree with n nodes and n-1 edges perform depth-first-traversal of it starting from the root node.

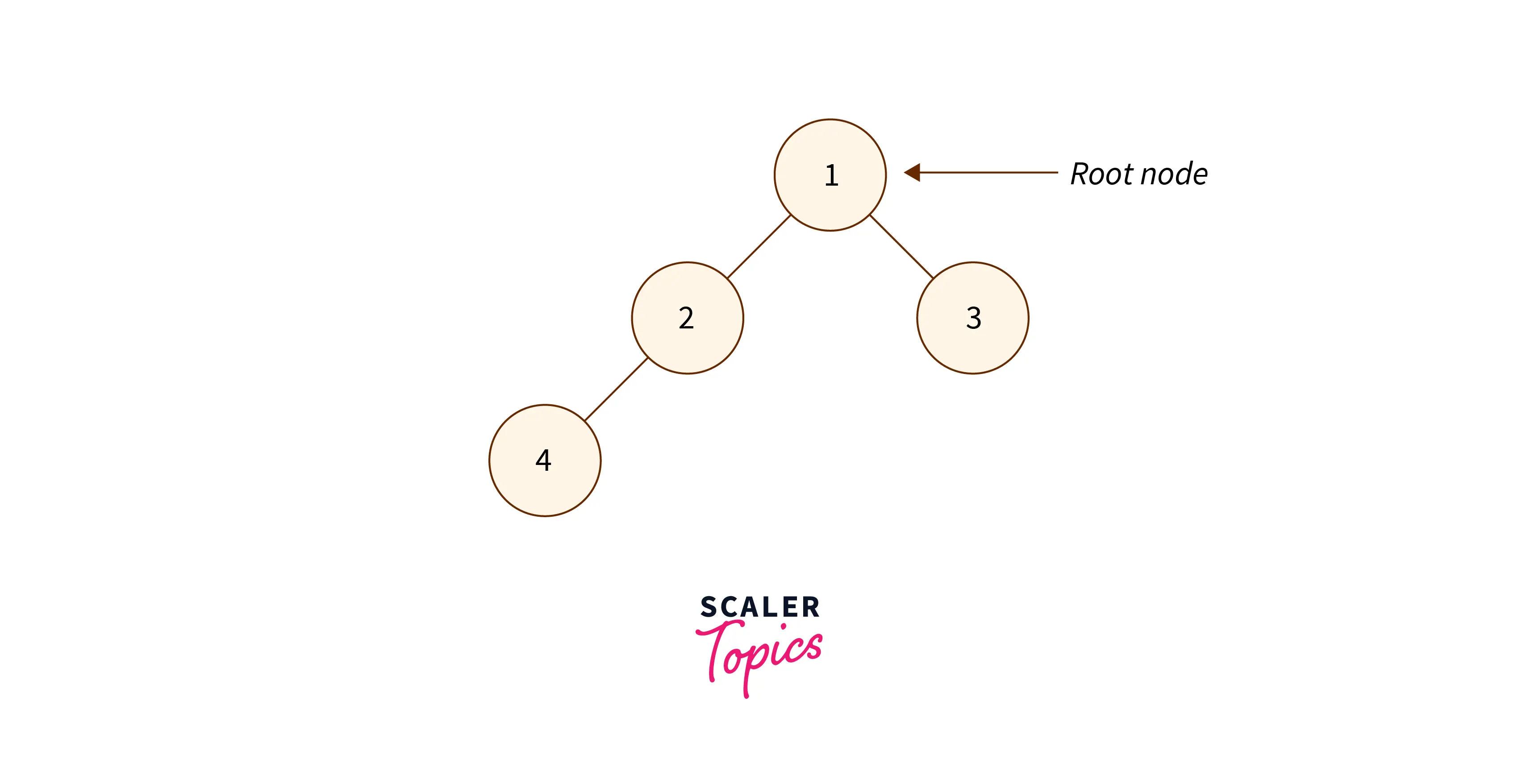
DFS call is made at the root node i.e. first node as DFS(1), a call stack will be activated immediatly where this call will be stored and it will keep calling the function recursively until leaf node is reached and function calls (activation records) will be stored for each such function call as follows:

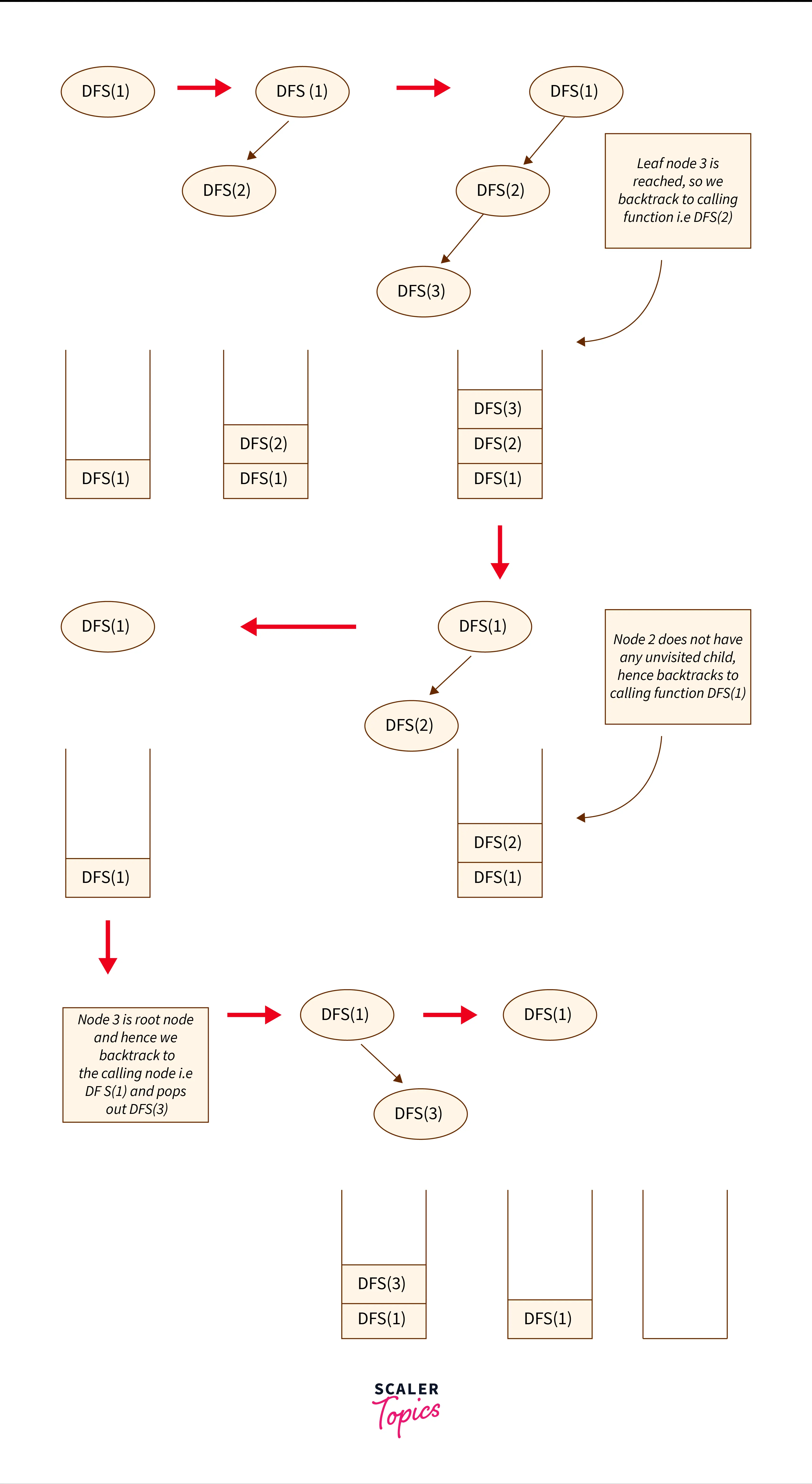
In this way, call stack is used.

Analysis Of Recursion

Highlights:

• Recursion technique is relatively more efficient than iterative technique in terms of time complexity according to modern CPU systems.
• Space complexity of recursive code is higher because of the consumption of call stack.

Recursion is a way of solving problems where a function calls itself directly or indirectly where the corresponding function is called recursive function, a recursive function solves a particular problem by solving the smaller problem where the solutoion of the smaller problem is uesd to build the solution of larger problem as in the above case the factorial of N is dependent upon the factorial of N-1, recursive approach is generally used in place of iterative approach because of readability and recursion is more efficient than iterations according to the latest enhanced CPU systems.

Let’s analyze the recursion using an example used in the introduction part i.e factorial of a number. The relevant recurrence relation is

fact(n) = n * fact(n-1)

Implementation

#include<bits/stdc++.h>
using namespace std;

int fact(int N){
    
    //Base condition
     if(N == 1)
         return 1;
    
    // Recurrence
     return N * fact(N-1);
}
int main(){
    
    // Input number
    int N = 5;
    
    // Call the factorial function
    int and = fact(N);
    
    //Print the answer
    coût << ans << "\n";
}

Output:

120

Let’s take an input of n = 4

Initially, fact(5) is called which recursively calls fact(4), fact(3), fact(2) , fact(1) and for n=1 i.e. base case it simply returns 1, then the recursion backtracks and solve the pending function calls in the stack as shown below:

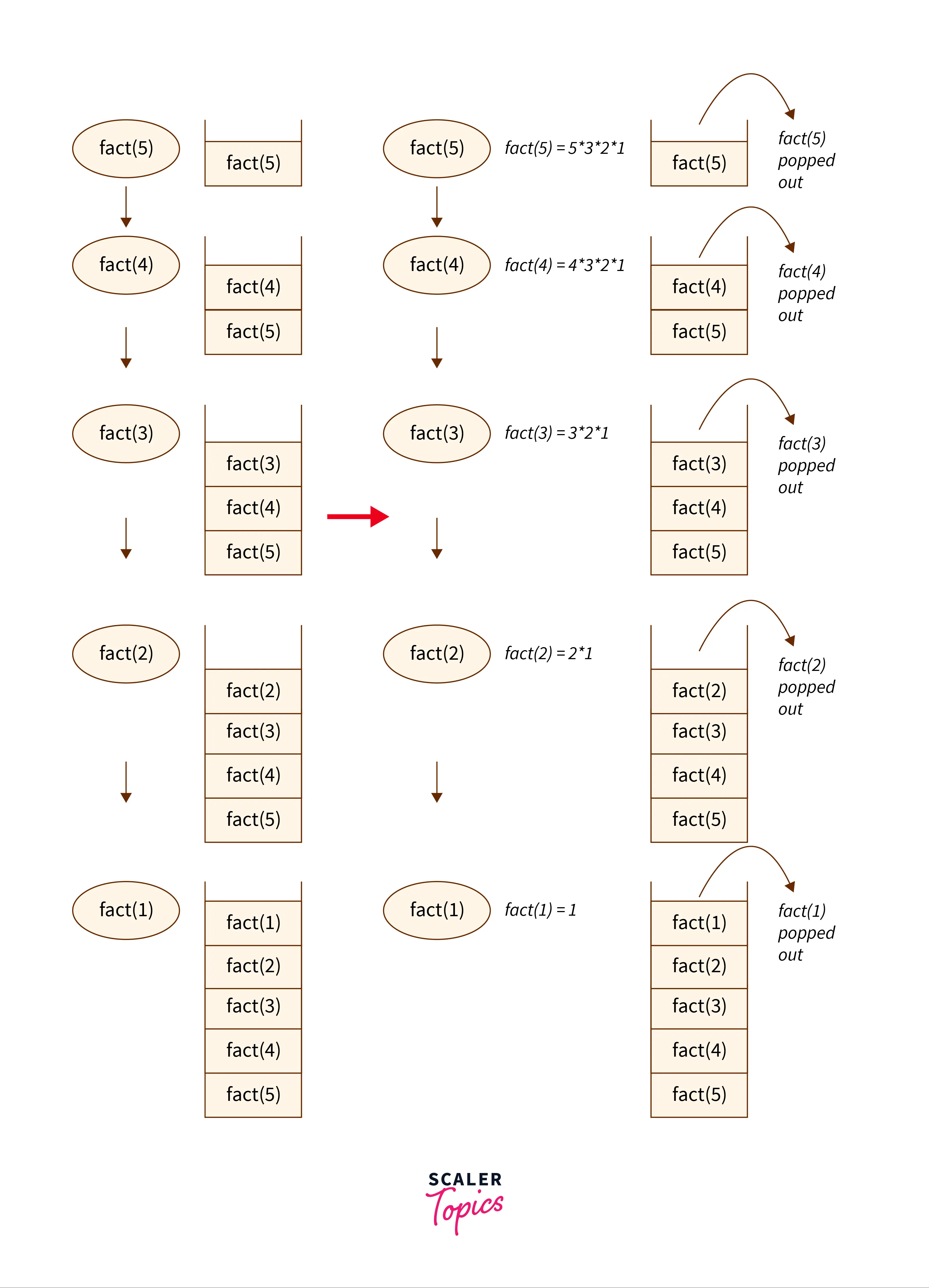
Let’s analyze the time and space complexity of the recursion.

Time Complexity

Highlights:

• Time complexity of recursion is the number of calls made to the function.

In the case of an iterative solution, the time complexity is analyzed as the number of iterations made i.e. traversing an array of size N takes N iterations and hence the time complexity O(N) while in the case of recursion the time complexity of a function call is O(1) while for N recursive calls the time complexity becomes O(N) as in the case of the DFS on a tree, we saw that there will be exactly N recursive calls at max in the call stack.

There are some cases where more than one recursive calls are made for each function call for example the case of fibonacci series f(n) = f(n-1) + f(n-2) Here, for each function call, there will be two function calls and it will become a tree of 2^n function calls and hence the time complexity becomes O(2^n). The corresponding recursion tree is as follows

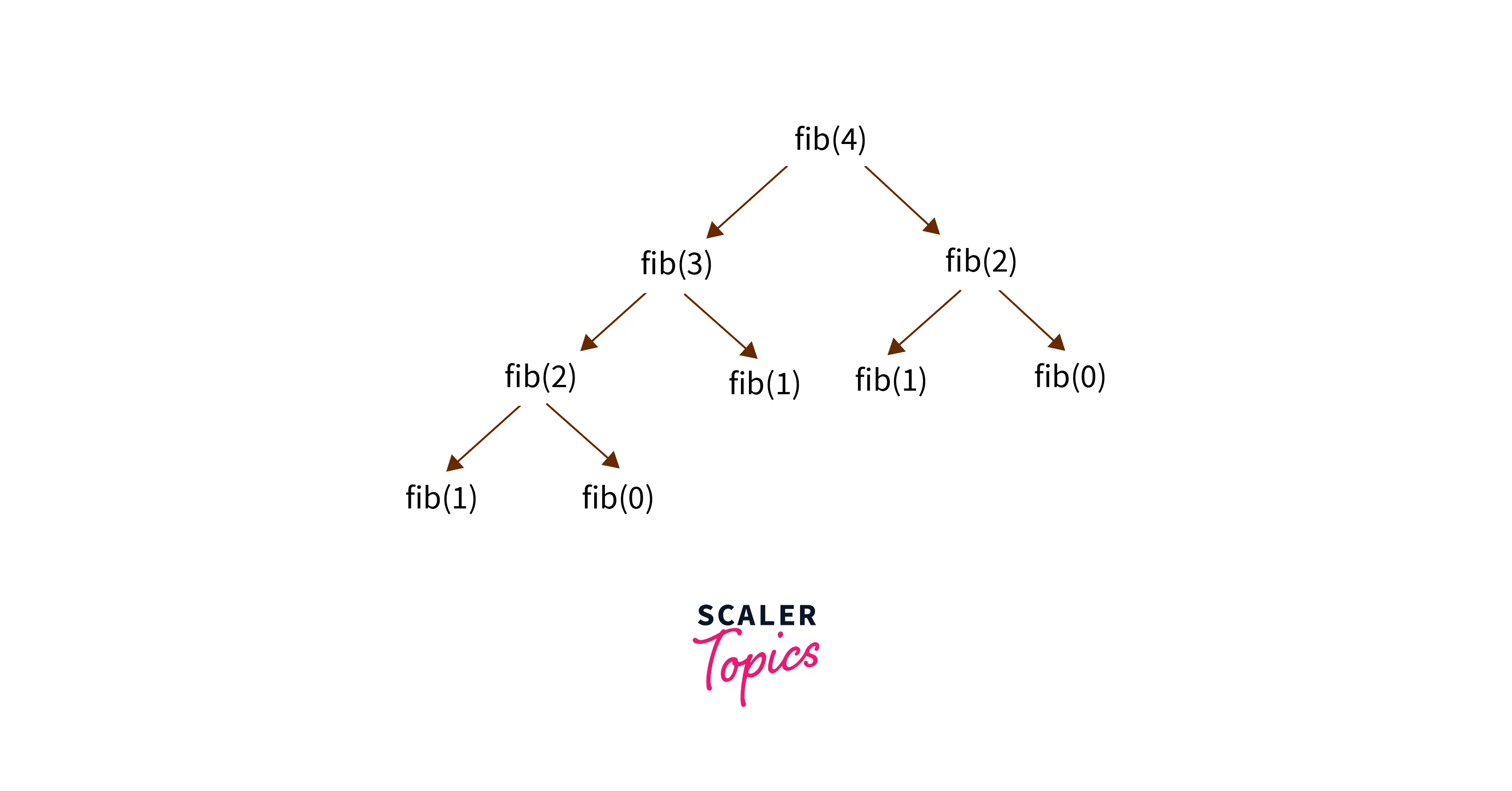
We can observe that at each node there are atmost two calls made which makes an upper bound time complexity of O(2^n).

Space Complexity

Highlights:

• Space complexity of the recursion is equal to the number of function calls made.

In case of iterations the compiler does not need any extra space for temporarily storing variables, arguments or addresses as it keeps on updating the values along with the iterations while in case of recursion, it needs to store the activation record in the call stack and hence it requires the extra space which may go up to O(N) in case when there aare at most N calls in the stack.

Learn More

To learn more about the stack data structure, its various implementations, operations and applications, read stack data structure article.

Conclusion

• We conclude that stack data structure is used to implement recursion.
• Stack is used for storing the activation record of a function call which contains arguments, local variables, and the address of the calling function.
• Space complexity of the recursive function equals the number of calls made to the function as the same number of activation records will be stored in the call stack.
• Time complexity of the recursive function equals the number of calls made to the function.
• Recursion technique of solving a problem is relatively more efficient in terms of time complexity according to the enhanced CPU systems.