Largest Number Formed from an Array

Problem Statement

Given an array of N positive integers, arrange these integers in such a manner that when we join the elements, it is maximum among all possible permutations of the array elements.

(Basically: Find the Largest Number Formed From an Array)

Example

Input:

arr = [3, 30, 40, 9]

Output:

[9, 40, 3, 30]

Example Explanation

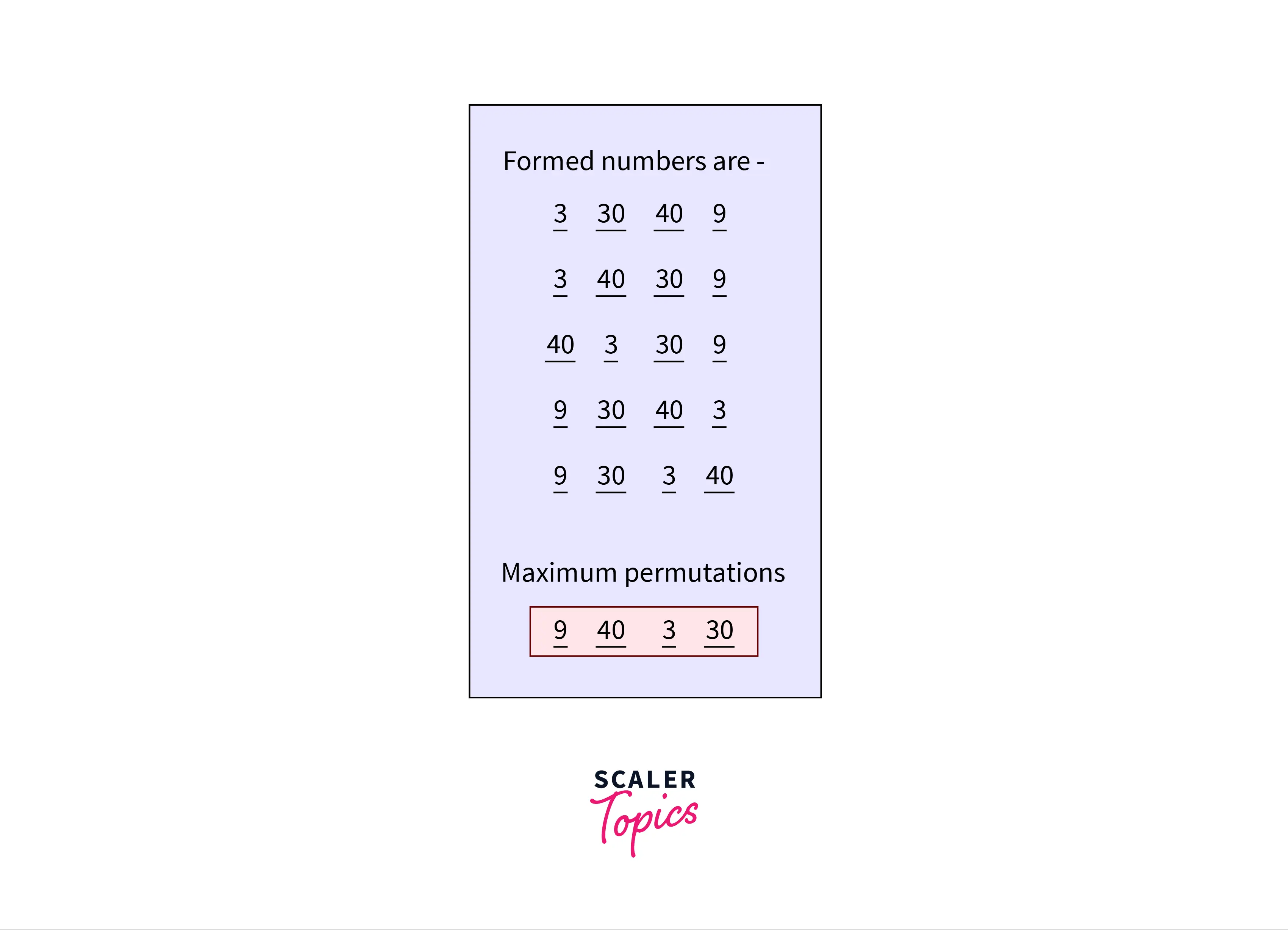
The given set of integers can be combined in the following ways:

• 330409
• 340309
• 403039
• 930340
• 933040
• 940330 … and so on.

A total of 4!=24 permutations are possible. The task is to find the permutation which yields the maximum number.

Therefore for the given input, the largest number formed from the elements of the array is 940330. This is clearly explained using the below image:

Input

Input format during competitive programming consists of an array with N number of integers.

Output:

Output format includes printing the modified array which is in the format of the largest number formed from the elements of the array which is given as input.

Constraints

• 1 <= N (length of the array) <= 10⁸
• 1 <= arr[i] <= 10⁴

Approach 1

The first idea we get as soon we see this problem is using sorting. Let’s assume we have the array consisting of elements [3, 9, 20, 640]. If we sort this set of integers in descending order we get [640, 20, 9, 3]. Now by combining these integers, we get a number 6402093, but the largest number formed from the elements of the given array is 9640320.

• Therefore, simple sorting doesn’t give the largest number because 640 is greater than 9 but arranging them in descending order, doesn’t yield the largest number formed from the array elements.
• So, this sorting technique should be modified a bit to obtain the largest number from the given set of elements. The modification includes sorting based on the comparison AB and BA as explained below.
• Assume the numbers taken are A and B, instead of comparing just values of A and B, compare by concatenating(combining) them as AB and BA.
• For example, if AB is greater than or equal to BA during the sorting process then we don’t need to swap the values of A and B in the array.

Algorithm

Below is the algorithm which clearly explains the comparison-based sorting for forming the largest number from given array elements, which is a stable sorting technique because it does not swap the elements if they’re of same value while comparing: For finding the largest number from the array of elements we need to do a little modification to the sorting technique which is discussed below. Consider two nested for loops with iterators i and j respectively.

• The first loop with iterator i starts from 0 to the length of the array.
• The second loop with iterator j starts from i to the length of the array.
  • For every two elements arr[i] and arr[j], convert them to strings. Let the strings be A and B, where A = string(arr[i]) and B = string(arr[j]).
  • Now combine them as AB and BA, and compare the values by converting them into an integer.
  • So, this simply means if int(AB)<int(BA), we need to swap the position of the numbers B and A in the array.
  • Else we don’t need to swap these numbers.

At last return the modified array by swapping wherever it is needed.

Implementation

Below is the implementation of the largest number formed from the array elements using comparison sort in languages like C++, python, and java.

C++ implementation of the largest number using array elements by comparison sort which is we need to add comparator in the sorting algorithm for comparison based sorting:

#include <algorithm>
#include <iostream>
#include <string>
#include <vector>
using namespace std;
 
// comparison sort using the logic explained in the algorithm
int myCompare(string A, string B) {
    // first form the AB by string concatenation
    string AB = A.append(B);
 
    // form the BA by string concatenation
    string BA = B.append(A);
 
    // compare if AB> BA we need to swap the elements
    return AB.compare(BA) > 0 ? 1 : 0;
}

vector<int> ans;

// function which modifies the position of elements in the array 
// by comparing two elements in the way explained
void LargestNumber(vector<string> &arr) {
    // calling the sort function
    sort(arr.begin(), arr.end(), myCompare);
    return;
}
 
// Driver code
int main() {
    // input array elements are taken as strings 
    // for simplicity of the process
    vector<string> arr;
 
    // push all these elements into the array 
    arr.push_back("3");
    arr.push_back("30");
    arr.push_back("40");
    arr.push_back("9");
    
    // calling the function to print the largest number formed
    LargestNumber(arr);
    
    // printing the elements in the modified array
    int N = arr.size();
    for(int i=0; i < N; i++)
        cout<<arr[i]<<" ";
    return 0;
}

Output:

9 40 3 30

Python implementation of the largest number formed from the array elements by comparison sort. This comparison sort is a modification of selection sort technique:

def largest_NumberFormed(arr):
    # Base case, if there is only one element, 
    # return the element because it is the only largest element formed  
    if len(arr)==1: 
        return str(array[0])
    
    # Convert all the elements into strings for combining them.
    for i in range(len(arr)):
        # convert it into strings
        arr[i]=str(arr[i])
        
    # Use two for loops to decide the relative position of any two elements
    for i in range(len(arr)):
        for j in range(i+1,len(arr)):
            # As discussed in the algorithm if BA>AB, 
            # we need to swap the positions of A and B
            # Here A is arr[i] and B is arr[j]
            if arr[j]+arr[i]>arr[i]+arr[j]:
                # swap these elements if they satisfy the above conditions
                arr[i],arr[j]=arr[j],arr[i]
    
    ans=[]
    for i in arr:
        ans.append(int(i))
        
    return ans
    
# Driver Code         
if __name__ == "__main__":
    # Input array of elements
    arr = [3, 30, 40, 9]
    
    # print the modified array after forming the largest number 
    print(largest_NumberFormed(arr))

Output:

[9, 40, 3, 30]

Java implementation of the largest number formed from the array elements by comparison sort:

import java.util.*;
 
class Solution {
    // method which gives the largest number from given array of elements
    static void LargestNumber(Vector<String> arr) {
        // Comparison sort is done which is explained in the 
        Collections.sort(arr, new Comparator<String>() {
            @Override 
            public int compare(String A, String B) {
 
                // first form the AB by string concatenation
                String AB = A + B;
 
                // form the BA by string concatenation
                String BA = B + A;
                
                // compare if AB> BA we need to swap the elements
                return AB.compareTo(BA) > 0 ? -1 : 1;
            }
        });
 
        Iterator itr = arr.iterator();
 
        while (itr.hasNext())
            //printing the modified elements 
            System.out.print(itr.next()+" ");
    }
 
    // Driver code
    public static void main(String[] args) {
         // input array elements are taken as strings 
         // for simplicity of the process
        Vector<String> arr;
        arr = new Vector<>();
        
        // push all these elements into an array 
        arr.add("3");
        arr.add("30");
        arr.add("40");
        arr.add("9");
        // calling the function to print the largest number
        LargestNumber(arr);
    }
}

Output:

9 40 3 30

Example Explanation:

The given set of integers can be combined in the following ways: 330409, 303409, 403039, 930340, 933040,.. and so on. There are many combinations present. Therefore for the given input, the largest number formed from the elements of the array is 940330.

Time Complexity: $O(N^2)$, where N is the length of the array which is given as input.

• This $O(N^2)$ time complexity is taken for the comparison based sorting which is a basic modification of the selection sort technique.
• Comparison-based sorting is considered to have a time complexity of $O(N^2)$. Because we need to check for every element and compare it with all the elements on the right side and swap whenever the condition is satisfied.
• Swapping the elements is not a costly operation, because it has the time complexity $O(1)$.
• So the overall time complexity for finding the largest number formed from the given array elements using comparison sorting is $O(N^2)$.

Space Complexity: $O(1)$

• Constant space is required to perform in-place sorting in the algorithm mentioned above.

Approach 2: Only in Python

In python, we can use itertools to find the largest number formed from the given array of elements. The itertools is a module in python that provides us with a collection of functions to handle different iterators.

The itertools module in python is a fast, memory-efficient module that utilizes the system’s computational resources efficiently. So, we use this module to find the largest number from the given array of elements for fast computation.

We can arrange these numbers in many ways and we get many different permutations by the arrangement of these array elements and we need to return the largest among all these permutations. In python we have class permutations which is present in the itertools module, so we import that for the simplification process and check for the largest among the formed permutations and return the largest number formed from the given array elements.

Algorithm

• The idea is to import permutations from itertools module.
• The second step includes storing all the permutations of these array elements.
• Each permutation of the array is converted to a string (representing the number) using the join() function.
• We need to return the largest number formed from all these permutations or strings. This can be done using the in-built max() function in python.

Note: Permutations are the different arrangements of this numbers. Generally these permutations are created by running two nested for loops on the given array. This whole process is actually included in the permutations class of the itertools module in python.

Implementation

Python implementation for finding the largest number from the given array elements using class permutations from the itertools module.

# Python3 implementation for finding the largest number using permutations
# importing the required class from the itertools module
from itertools import permutations
def largestNumberFormed(arr):
    ans = []
    for i in permutations(arr, len(arr)):
        # provides all permutations of the arr, 
        # store them in the list, and finds the maximum among it
        ans.append("".join(map(str,i)))

    return max(ans)

# Input array of elements
# print the modified array after forming the largest number 
arr=[3, 30, 40, 9]

# return the largest number formed from the given array elements 
# permutations can also be increased using recursion
print(largestNumberFormed(arr))

Output:

940330

Example Explanation:

The given set of integers can be combined in the following ways: 330409, 303409, 403039, 930340, 933040,.. and so on. There are many combinations present. Therefore for the given input, the largest number formed from the elements of the array is 940330.

Complexity Analysis

Time Complexity: $O(N!)$, where N is the length of the array that is given as input.

• Each permutation of the input array is calculated in $O(1)$ time. Since N! number of permutations are possible, the overall time complexity of finding all permutations is $O(N!)$.
• And giving the maximum among this N! the number of permutations takes a time complexity of $O(N!)$. Therefore the overall time complexity is $O(N!)$$ for finding the largest number formed from all the array elements permutations.

Space Complexity: $O(N!)$, where N is the length of the array that is given as the input.

• $O(N!)$ space is needed to store all the permutations possible from the given input elements of the array and get the largest number from all those permutations.

Conclusion

• For finding the Largest number formed from an array of elements is discussed using two different approaches.
• The first approach to finding the largest number formed from an array includes comparator-based sorting because a simple sorting technique yields wrong answers as discussed earlier.
• We will decide the relative position of two elements A and B by comparing AB and BA. If BA>AB, B should come first, otherwise A.
• It is a stable sorting technique that is used for finding the largest number from the given array of elements.
• This method has the time complexity of $O(N^2)$ and the space complexity is $O(1)$.
• The second method for finding the largest number formed from an array elements is achieved using the itertools module in Python.
• It contains the permutations() function which computes all permutations of the input container recursively. It has the time complexity of $O(N!)$ and space complexity of $O(N!)$.
• Out of these two methods, the first method i.e., comparison-based sorting is preferable because it is considered to be more efficient in both time and space complexity-wise for finding the largest number from the given array of elements.