Traversing in the data structure is a very important operation that can be performed on any data structure. Traversing in Data Structure means systematically visiting every element of it. Traversing is a process in which each element of a data structure is accessed. Accessing an element of data structure means visiting every element at least once. Traversing is performed to display every element of data structure or to perform any operation on its element. Traversing is also known as iterating over the data structure.
Takeaways
Traversing operation is used to access elements of data structure or to perform some operation on elements.
What is the Traversal of a Binary Tree?
A binary tree is a data structure in which data is stored in a hierarchical form. Traversal of the binary tree means visiting every node of the tree. The process of accessing the nodes of a tree in some order is called a traversal of a binary tree. Any process for visiting all of the nodes is called a traversal.
What is the Traversing of a Linked List?
A linked list is a data structure that we will traverse from the head node to the last node of the list. Traversing a linked list means visiting every node of the linked list to perform some operation on the nodes.
What is Traversal Order?
Unlike linear data structures(Array, Queues, Linked List, Queues, etc.) that have only one way to traverse them but the tree data structure can be traversed in multiple ways.
The tree can be traversed in three ways:
In-order Traversal
In inorder to traversal of the binary tree,
- Firstly left subtree is visited
- Then the root is visited
- The right subtree is visited.
Above 3 steps are recursively performed.
An in-order traversal of the Binary Search Tree gives us the ascending order of values stored in the tree.
Pre-order Traversal
In pre-order traversal of a binary tree,
- Firstly root is visited
- Then the left subtree is visited
- Then finally the right subtree is visited.
Above 3 steps are recursively performed.
Post-order Traversal
In post-order traversal of the binary tree root node is visited at the last. In this
- Firstly left subtree is visited
- Then the right subtree is visited.
- And at last, the root is visited.
Above 3 steps are recursively performed.
Binary Tree Traversal Techniques
Traversing a binary tree means accessing every node of a tree.
The Tree can be traversed in three ways:
In-order Traversal
Algorithm
Algorithm Inorder(tree)
- Traverse the left subtree of the tree, call Inorder(left-subtree)
- Visit the root of the tree.
- Traverse the right subtree of the tree, call Inorder(right-subtree)
Example
Below is an image to show an example of the inorder traversal
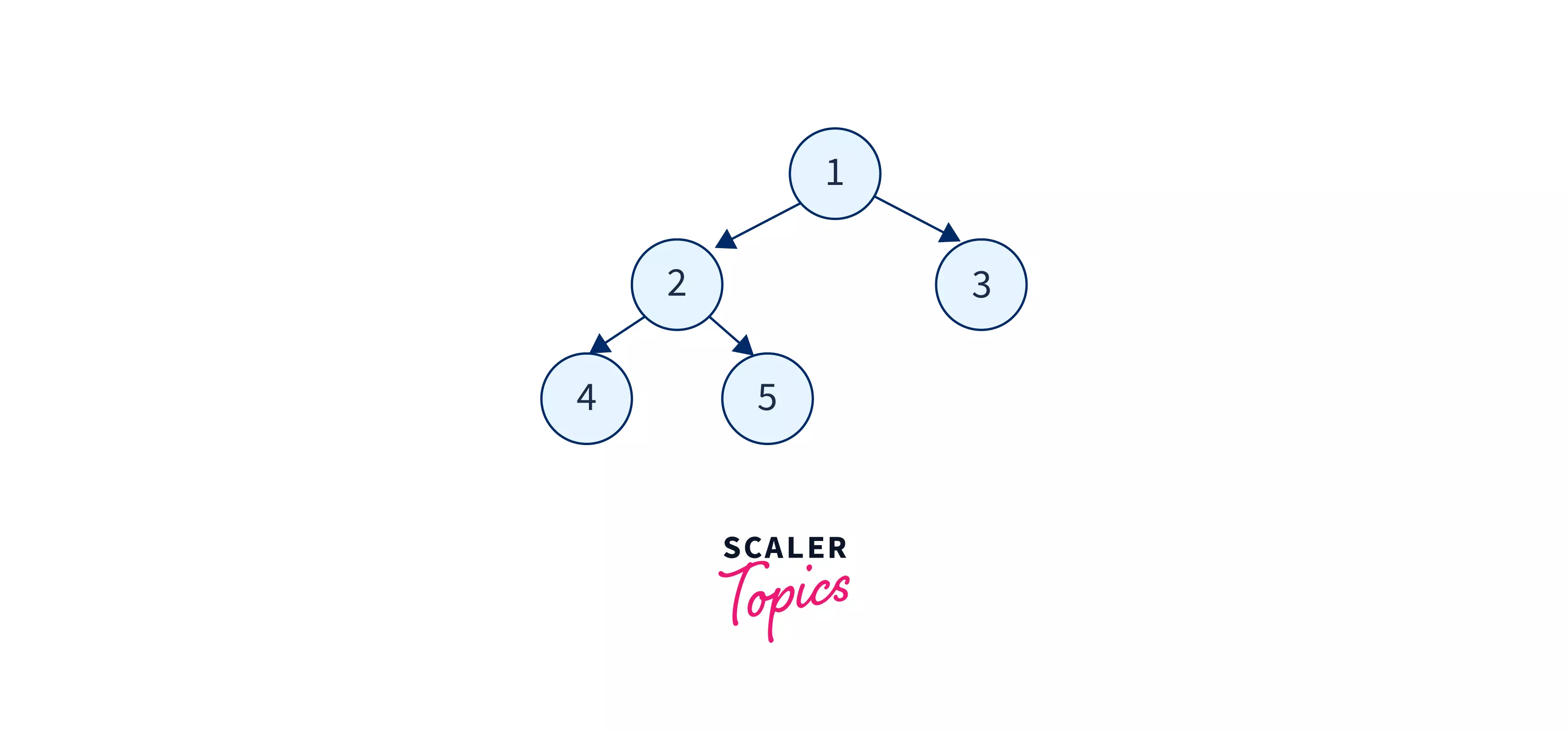
An in-order traversal of the above example is: 4 2 5 1 3
Pre-order Traversal
Algorithm Algorithm Preorder(tree)
- Visit the root of the tree.
- Traverse the left subtree of the tree, call Preorder(left-subtree)
- Traverse the right subtree of the tree, call Preorder(right-subtree)
Example
Below is an image to show an example of the preorder traversal
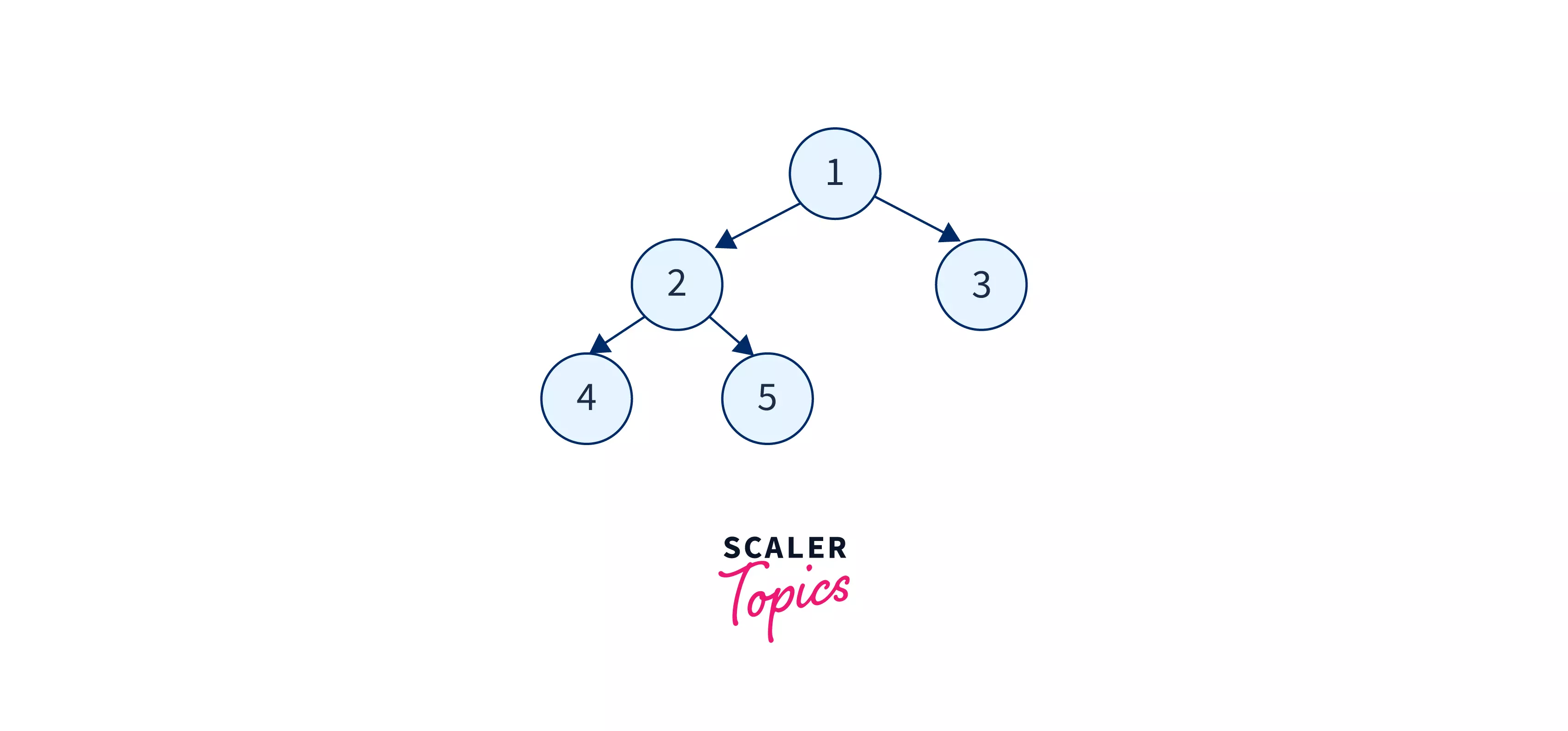
Pre-order traversal of the above example is: 1 2 4 5 3
Post-order Traversal
Algorithm
Algorithm Postorder(tree)
- Traverse the left subtree of the tree, call Postorder(left-subtree)
- Traverse the right subtree of the tree, call Postorder(right-subtree)
- Visit the root of the tree.
Example
Below is an image to show an example of the postorder traversal
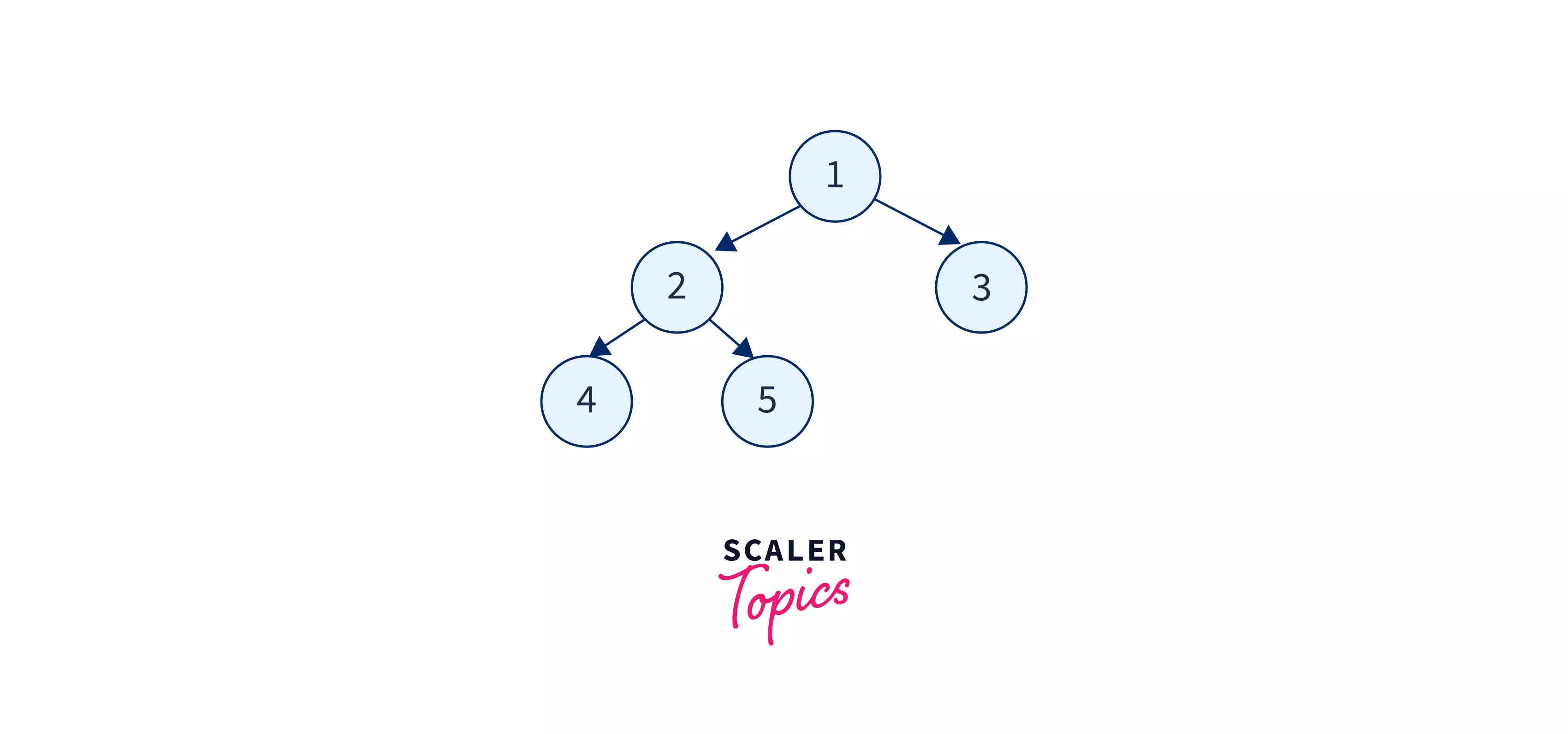
Post-order traversal of the above example is: 4 5 2 3 1
What are Tree Traversal Methods?
Traversal Implementation
C++ Implementation
// C++ program to display in-order, post-order, pre-order traversal of tree
#include <iostream>
using namespace std;
/* A binary tree node has data stored as value, pointer to left child
and right child */
struct Node {
int value;
struct Node *left, *right;
};
//function for creating new tree node
Node* createNode(int value){
Node* t = new Node;
t->value = value;
t->left = t->right = NULL;
return t;
}
/* printing postorder traversal of binary tree */
void postorder(struct Node* root){
if (root == NULL)
return;
// first traverse left subtree
postorder(root->left);
// then traverse right subtree
postorder(root->right);
// now visit root node
cout << root->value << " ";
}
/* inorder traversal of the binary tree*/
void inorder(struct Node* root){
if (root == NULL)
return;
/* first visit left child */
inorder(root->left);
/* print root data */
cout << root->value << " ";
/* at last recur over right subtree */
inorder(root->right);
}
/* Preorder traversal of the binary tree*/
void preorder(struct Node * root){
if (root == NULL)
return;
/* display node value */
cout << root->value << " ";
/* then traverse left subtree */
preorder(root->left);
/* now traverse right subtree */
preorder(root->right);
}
int main(){
struct Node* n = createNode(1);
n->left = createNode(2);
n->right = createNode(3);
n->left->left = createNode(4);
n->left->right = createNode(5);
cout << "\nPreorder traversal of tree: \n";
preorder(n);
cout << "\nInorder traversal of tree: \n";
inorder(n);
cout << "\nPostorder traversal of tree: \n";
postorder(n);
return 0;
}
Output
Preorder traversal of binary tree :
1 2 4 5 3
Inorder traversal of binary tree :
4 2 5 1 3
Postorder traversal of binary tree :
4 5 2 3 1
Java Implementation
// Java program for different tree traversals
/* Class containing left and right child of current
node and key value*/
class Node {
int data;
Node left, right;
public Node(int item){
data = item;
left = right = null;
}
}
class Tree {
// Root of Binary Tree
Node root;
Tree() { root = null; }
/* print postorder traversal of given tree. */
void postorder(Node root){
if (root == null)
return;
// first traverse left subtree
postorder(root.left);
// then traverse right subtree
postorder(root.right);
// at last print root value
System.out.print(root.data + " ");
}
/* print inorder traversal of binary tree*/
void inorder(Node root){
if (root == null)
return;
/* first trvarese left subtree */
inorder(root.left);
/* then print the data of node */
System.out.print(root.data + " ");
/* at last trvaerse right subtree */
inorder(root.right);
}
/* printing preorder traversal of binary tree*/
void preorder(Node root){
if (root == null)
return;
/* print node value */
System.out.print(root.data + " ");
/* then traverse left subtree */
preorder(root.left);
/* now traverse right subtree */
preorder(root.right);
}
// calling functions for traversals of binary tree
void postorder() {
postorder(root);
}
void inorder() {
inorder(root);
}
void preorder() {
preorder(root);
}
public static void main(String[] args){
Tree t = new Tree();
t.root = new Node(1);
t.root.left = new Node(2);
t.root.right = new Node(3);
t.root.left.left = new Node(4);
t.root.left.right = new Node(5);
System.out.println(
"Preorder traversal of tree : ");
t.preorder();
System.out.println(
"\nInorder traversal of tree : ");
t.inorder();
System.out.println(
"\nPostorder traversal of tree : ");
t.postorder();
}
}
Output
Preorder traversal of binary tree :
1 2 4 5 3
Inorder traversal of binary tree :
4 2 5 1 3
Postorder traversal of binary tree :
4 5 2 3 1
Python Implementation
# Python program for tree traversals
# A class that represents an individual node in a
# Binary Tree
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.data = key
# printing inorder tree traversal
def inorder(node):
if node:
# First traverse left subtree
inorder(node.left)
# then print the node data
print(node.data),
# now traverse right subtree
inorder(node.right)
# postorder tree traversal of binary tree
def postorder(node):
if node:
# traverse left subtree
postorder(node.left)
# recur on the right child
postorder(node.right)
# print node value
print(node.data),
# A function to do preorder tree traversal
def preorder(node ):
if node:
# print node value
print(node.data),
# recur on left child
preorder(node .left)
# at last recur on right child
preorder(node .right)
# Driver code
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print("Preorder traversal of binary tree :")
preorder(root)
print("\nInorder traversal of binary tree :")
inorder(root)
print("\nPostorder traversal of binary tree :")
postorder(root)
Output
Preorder traversal of binary tree :
1 2 4 5 3
Inorder traversal of binary tree :
4 2 5 1 3
Postorder traversal of binary tree :
4 5 2 3 1
Examples for Traversing in the Data Structure
Array Traversal Example
Below is an image to show an example of the array traversal
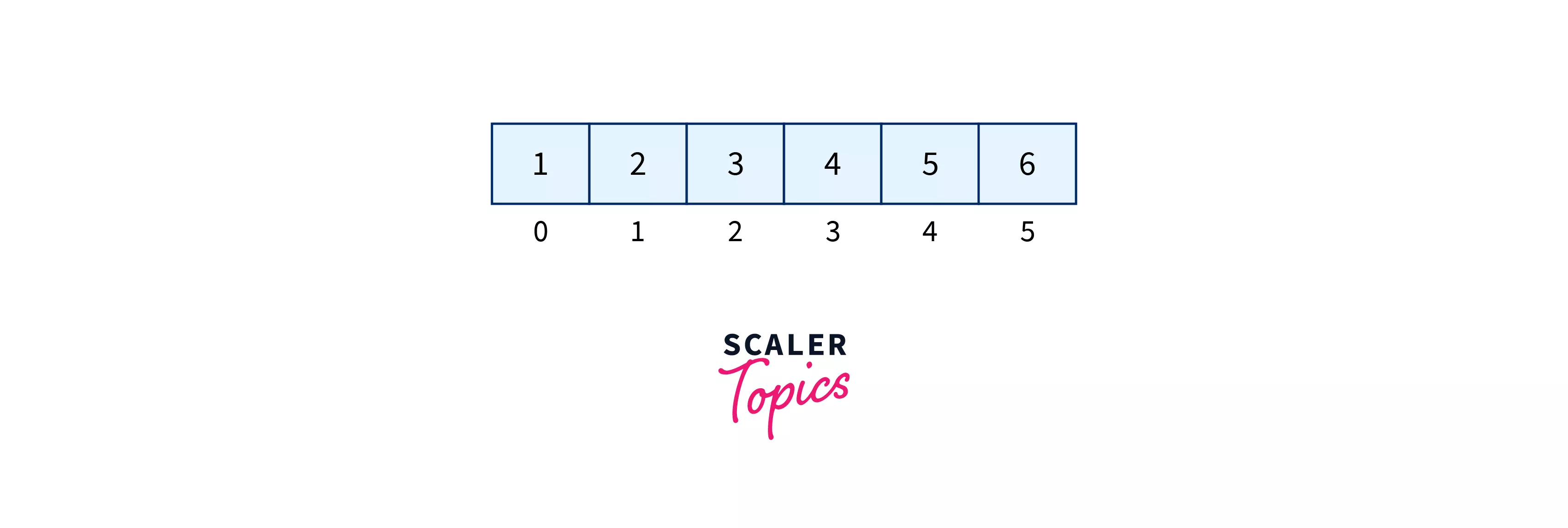
Traversal of the above array is 1,2,3,4,5,6
Linked List Traversal Example
Below is an image to show an example of the linked list traversal
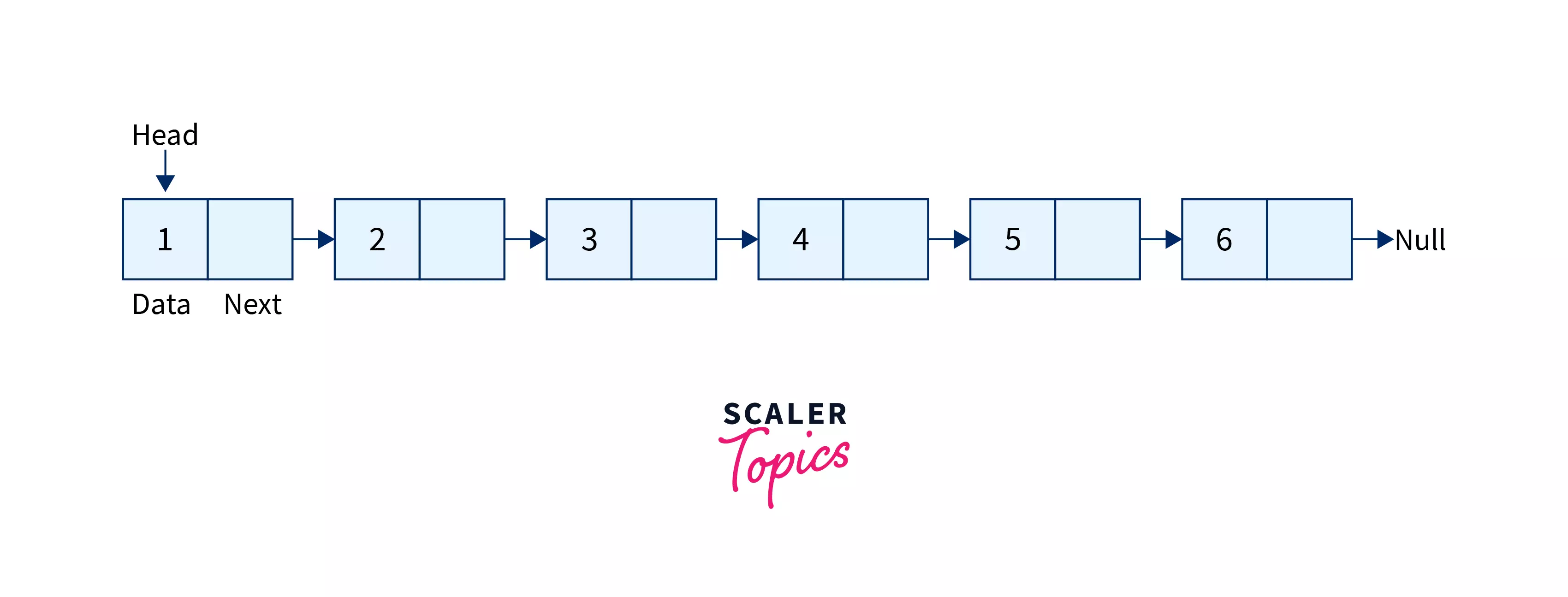
Traversal of the above-Linked List is 1,2,3,4,5,6
Learn about Graph Traversal in Data Structure
Let us take a recap of Graph Traversal
In graph traversal, every node of the graph is visited at least once. Two techniques are used for graph traversal, i.e. Depth First Search and Breadth-First Search.
Boost your C++ proficiency with expertly designed Data Structures in C++ Course by Scaler Topics. Get started now!
Conclusion
- Traversing a data structure is a very important operation that can be performed on data structures like an array, linked list, tree, graph, etc.
- Traversing means accessing each element of data structure at least once.
- Linked List traversal means accessing all the elements of the list starting from the head node to the last node.
- Traversing a tree and graph means visiting every node at least once.
- In-tree data structure, we have three types of traversal: In-order traversal, Pre-order traversal, and Post-order traversal.
- In the graph, we have Depth First Search and Breadth-First Search for traversing.