Separate Chaining is one of the techniques that is used to resolve the collision. It is implemented using linked lists. This method combines a linked list with a hash table in order to resolve the collision. In this method, we put all the elements that hash to the same slot in the linked list.
Scope of article
- This article defines the
Separate Chainingcollision resolution technique and explains the intuitive logic of this algorithm. We will also see the time complexity of searching and deletion of the element in the hash table. - This article also shows a fully working example to understand the logic of the method. But it does not compare Separate Chaining with other collision resolution techniques.
Takeaways
The biggest advantage of separate chaining is its collision avoidance capabilities. This means that many data items may be hashed with the same keys creating long link chains.
What is Separate Chaining?
Separate Chaining is the collision resolution technique that is implemented using linked list. When two or more elements are hash to the same location, these elements are represented into a singly-linked list like a chain. Since this method uses extra memory to resolve the collision, therefore, it is also known as open hashing.
Separate Chaining Hash Table
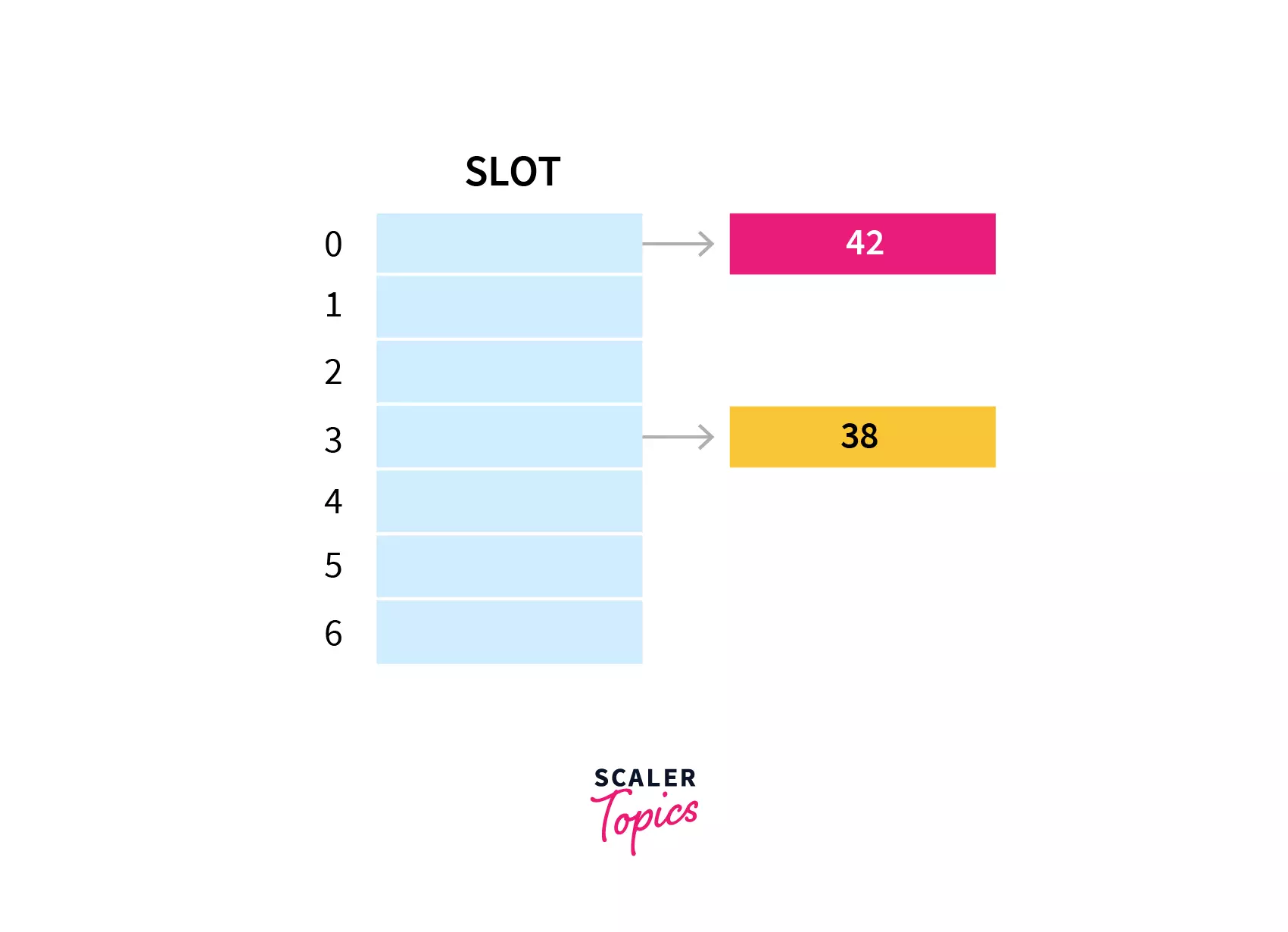
In separate chaining, each slot of the hash table is a linked list. We will insert the element into a specific linked list to store it in the hash table. If there is any collision i.e. if more than one element after calculating the hashed value mapped to the same key then we will store those elements in the same linked list. Given below is the representation of the separate chaining hash table.
Example: Let’s understand with the help of examples. Given below is the hash function:
h(key) = key % table size
In a hash table with size 7, keys 42 and 38 would get 0 and 3 as hash indices respectively.
If we insert a new element 52 , that would also go to the fourth index as 52%7 is 3.
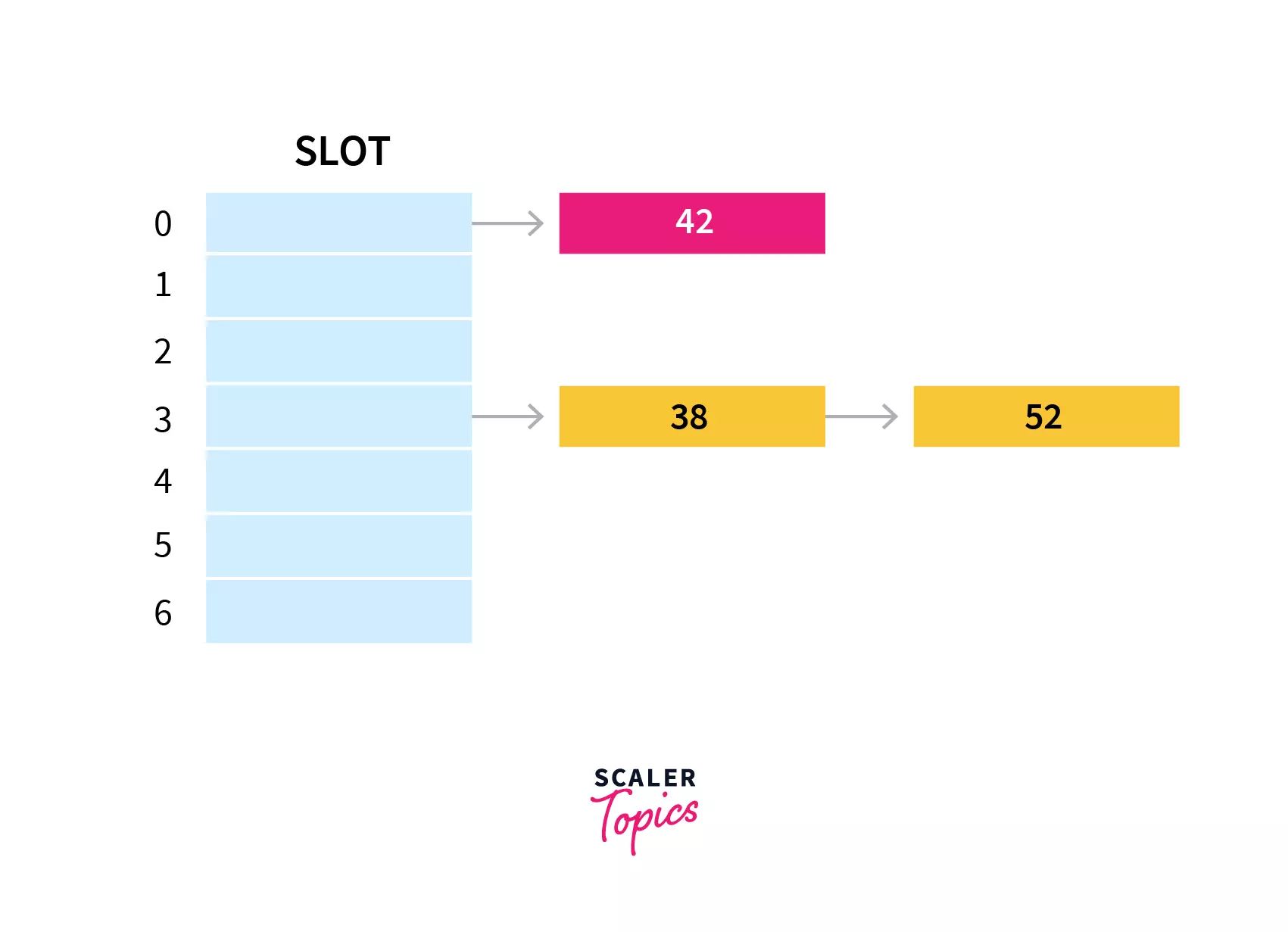
The lookup cost will be scanning all the entries of the selected linked list for the required key. If the keys are uniformly distributed then the average lookup cost will be an average number of keys per linked list.
How to Avoid Collision in Separate Chaining Method
Separate chaining method handles the collison by creating a linked list to the occupied buckets. So far we only looked at a simple hash function where collision is imminent. It is important to choose a good hash function in order to minimize the number of collisions so that all the key values are evenly distributed in the hash table. Some characterstics of good hash function are:
- Minimize collisions
- Be easy and quick to compute
- key values inserted evenly in the hash table
- Have a high load factor for a given set of keys
Time Complexity
- In case of searching: The average time complexity of the search operation with the chaining method is
O(1+load factor)i.e. it takes time proportional to a chain of the linked list created which is the same for all the slots. - The worst case occurs when all the elements are inserted into the same linked list. In such a case, a linear search will have to be performed in order to search for the particular key. So in the worst-case time complexity of searching is
O(n)where n is the number of keys hash to the same slot, creating a list of length n. - In case of deletion: In order to delete a key first we need to search the key and then only we can delete it. In average case the time complexity of deletion is
O(1+ load factor). But in worst case the time complexity of the search operation isO(n). So, the time complexity of deleting a particular key in worst case is alsoO(n).
Load Factor:
The load factor of the hash table can be defined as the number of items the hash table contains divided by the size of the hash table. Load factor is the decisive parameter that is used when we want to rehash the previous hah function or want to add more elements to the existing hash table.
It helps us in determining the efficiency of the hash function i.e. it tells whether the hash function which we are using is distributing the keys uniformly or not in the hash table.
Load Factor= Total elements in hash table/ Size of hash table
Practice Problem Based on Separate Chaining
Let’s take an example to understand the concept more clearly. Suppose we have the following hash function and we have to insert certain elements in the hash table by using separate chaining as the collision resolution technique.
Hash function = key % 6
Elements = 24, 75, 65, 81, 42, and 63.
Let’s see step by step approach on how to solve the above problem.
Step 1: First we will draw the empty hash table which will have a possible range of hash values from 0 to 5 according to the hash function provided.
Step 2: Now we will insert all the keys in the hash table one by one. First key to be inserted is 24. It will map to bucket number 0 which is calculated by using hash function 24%6=0.
Step 3: Now the next key that is need to be inserted is 75. It will map to the bucket number 3 because 75%6=3. So insert it to bucket number 3.
Step 4: The next key is 65. It will map to bucket number 5 because 65%6=5. So insert it to bucket number 5.
Step 5: Now the next key is 81. Its bucket number will be 81%6=3. But bucket 3 is already occupied by key 75. So separate chaining method will handles the collision by creating a linked list to bucket 3.
Step 6: Now the next key is 42. Its bucket number will be 42%6=0. But bucket 0 is already occupied by key 24. So separate chaining method will again handles the collision by creating a linked list to bucket 0.
Step 7: Now the last key to be inserted is 63. It will map to the bucket number 63%6=3. Since bucket 3 is already occupied, so collision occurs but separate chaining method will handle the collision by creating a linked list to bucket 3.
In this way the separate chaining method is used as the collision resolution technique.
Advantages
Separate Chainingis one of the simplest methods to implement and understand.- We can add any number of elements to the chain.
- It is frequently used when we don’t know about the number of elements and the number of keys that can be inserted or deleted.
Disadvantages
- The keys in the hash table are not evenly distributed.
- Some amount of wastage of space occurs.
- The complexity of searching becomes
O(n)in the worst case when the chain becomes long.
Summary
Separate Chainingtechnique combines a linked list with a hash table in order to resolve the collision.- This method uses extra memory to resolve the collision.
- The time complexity of both searching and deleting a element in the hash table is
O(n), where n is the number of keys hash to the same slot. - Load factor is used when we want to rehash the previous hash function or want to add more elements to the existing hash table.
Dive into the World of Efficient Coding – Enroll in Scaler Academy‘s DSA Course Today and Learn from Industry Experts!

