What is a Linked List ?
A linked list is a linear data structure. It is a collection of nodes, and a node contains data and addresses the next node. Linked lists do not use contiguous memory allocation for storage, unlike arrays.

What are the Applications of Linked List ?
There are many applications of linked lists, be it in computer science or the real world.
Some of these Applications are :
Applications of Linked List in Computer Science :
- Linked lists can be used to represent polynomials.
- Using a linked list, we can perform the polynomial manipulation.
- Arithmetic operations like addition or subtraction of long integers can also be performed using a linked list.
- The linked list can be used to implement stacks and queues.
- The linked list is also used in implementing graphs in which the adjacent vertices are stored in the nodes of the linked list popularly known as Adjacency list representation.
Applications of Linked Lists in the Real World :
- In music players, we can create our song playlist and can play a song either from starting or ending of the list. And these music players are implemented using a linked list.
- We watch the photos on our laptops or PCs, and we can simply see the next or previous images easily. This feature is implemented using a linked list.
- You must be reading this article on your web browser, and in web browsers, we open multiple URLs, and we can easily switch between those URLs using the previous and next buttons because they are connected using a linked list.
Applications of Circular Linked Lists :
- The circular linked list can be used to implement queues.
- In web browsers, the back button is implemented using a circular linked list.
- In an operating system, a circular linked list can be used in scheduling algorithms like the Round Robin algorithm.
- The undo functionality that is present in applications like photo editors etc., is implemented using circular linked lists.
- Circular linked lists can also be used to implement advanced data structures like MRU (Most Recently Used) lists and Fibonacci heap.
Applications of Singly Linked List :
- The singly linked list is used to implement stack and queue.
- The undo or redo options, the back buttons, etc., that we discussed above are implemented using a singly linked list.
- During the implementation of a hash function, there arises a problem of collision, to deal with this problem, a singly linked list is used.
Application of Doubly Linked Lists :
- The doubly linked list is used to implement data structures like a stack, queue, binary tree, and hash table.
- It is also used in algorithms of LRU (Least Recently used) and MRU(Most Recently Used) cache.
- The undo and redo buttons can be implemented using a doubly-linked list.
- The doubly linked list can also be used in the allocation and deallocation of memory.
Polynomial Manipulation
Polynomials are algebraic expressions that contain coefficients and variables. Polynomial manipulation is doing mathematical operations, like addition, subtraction, etc., on polynomials.
Polynomials are a very important part of mathematics, and there aren’t any direct data structures present that can be used to store polynomials in memory. Thus, we take the help of a linked list to represent a polynomial.
To represent the polynomials using a linked list, we assume that each node of the linked list corresponds to each term of the polynomials.
Let us see how a polynomial is represented in a linked list.
The node of the linked list contains three parts :
- the coefficient value,
- the exponent value, and
- the link to the next term.
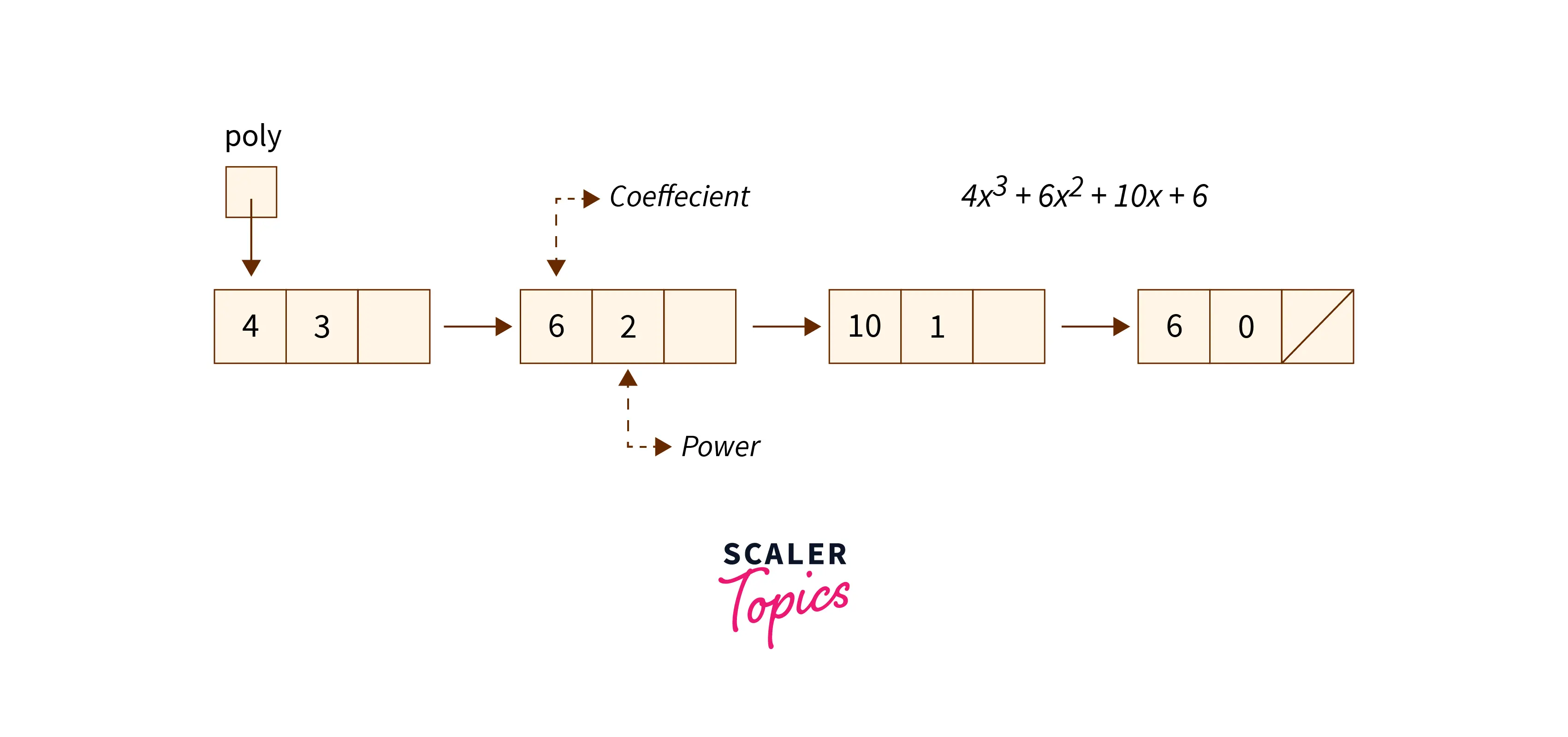
For example the polynomial 4×3+6×2+10x+64x3+6x2+10x+6 can be represented as
C++ Program for Addition of Two Polynomials
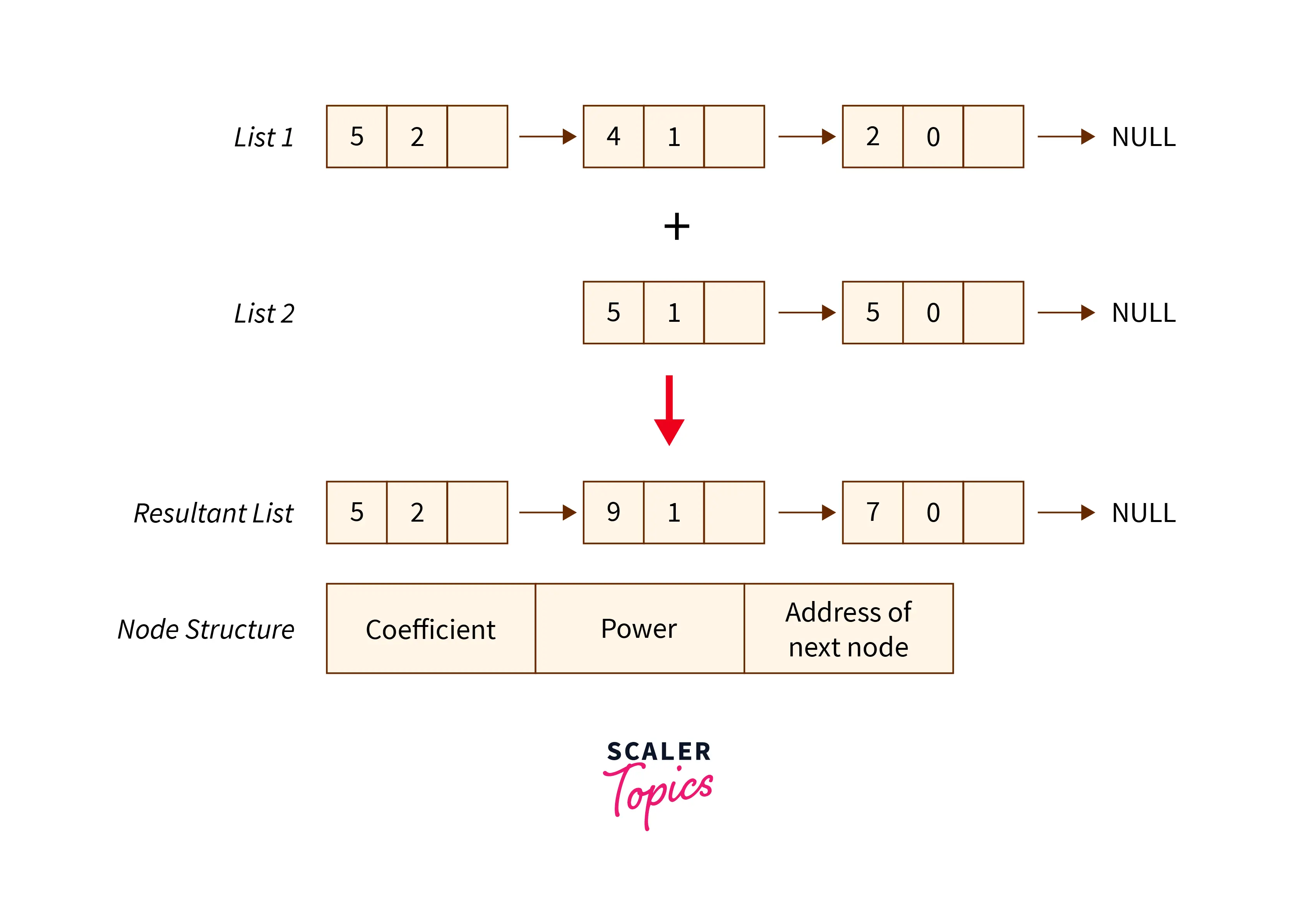
To add two polynomials, we first represent both of them in the form of a linked list. And then, we add the coefficients having the same exponent.
For example, suppose we want to add two polynomials that are : $5x^3 + 4x^2 + 2x^0$ and $5x^1 – 5x^0$.

C++ Program :
// program to add two polynomials
#include <bits/stdc++.h>
using namespace std;
// structure of a node
struct Node{
int co_eff;
int pwr;
struct Node* nxt;
};
// add new node
void make_newnode(int x, int y,
struct Node** temp){
struct Node *r, *z;
z = *temp;
if (z == NULL){
r = (struct Node*)malloc(sizeof(struct Node));
r->co_eff = x;
r->pwr = y;
*temp = r;
r->nxt = (struct Node*)malloc(sizeof(struct Node));
r = r->nxt;
r->nxt = NULL;
}
else{
r->co_eff = x;
r->pwr = y;
r->nxt = (struct Node*)malloc(sizeof(struct Node));
r = r->nxt;
r->nxt = NULL;
}
}
// add two polynomials
void add_poly(struct Node* first_poly,
struct Node* sec_poly,
struct Node* poly){
// if the degree of the first polynomial is
// greater than the second polynomial then
// do not change the first polynomial and move
// its pointer
while (first_poly->nxt &&
sec_poly->nxt){
if (first_poly->pwr > sec_poly->pwr){
poly->pwr = first_poly->pwr;
poly->co_eff = first_poly->co_eff;
first_poly = first_poly->nxt;
}
// if the degree of the second polynomial is
// greater than the first polynomial then
// do not change the second polynomial and move
// its pointer
else if (first_poly->pwr < sec_poly->pwr){
poly->pwr = sec_poly->pwr;
poly->co_eff = sec_poly->co_eff;
sec_poly = sec_poly->nxt;
}
// if the degree of both polynomials is
// same then add the coefficients
else{
poly->pwr = first_poly->pwr;
poly->co_eff = (first_poly->co_eff +
sec_poly->co_eff);
first_poly = first_poly->nxt;
sec_poly = sec_poly->nxt;
}
poly->nxt =
(struct Node*)malloc(sizeof(struct Node));
poly = poly->nxt;
poly->nxt = NULL;
}
while (first_poly->nxt || sec_poly->nxt){
if (first_poly->nxt){
poly->pwr = first_poly->pwr;
poly->co_eff = first_poly->co_eff;
first_poly = first_poly->nxt;
}
if (sec_poly->nxt){
poly->pwr = sec_poly->pwr;
poly->co_eff = sec_poly->co_eff;
sec_poly = sec_poly->nxt;
}
poly->nxt =
(struct Node*)malloc(sizeof(struct Node));
poly = poly->nxt;
poly->nxt = NULL;
}
}
// print the linked list
void display_poly(struct Node* node){
while (node->nxt != NULL){
printf("%dx^%d", node->co_eff,
node->pwr);
node = node->nxt;
if (node->co_eff >= 0){
if (node->nxt != NULL)
printf("+");
}
}
printf("\n");
}
// main function
int main(){
struct Node *first_poly = NULL,
*sec_poly = NULL,
*poly = NULL;
make_newnode(5, 2, &first_poly);
make_newnode(4, 1, &first_poly);
make_newnode(2, 0, &first_poly);
make_newnode(-5, 1, &sec_poly);
make_newnode(-5, 0, &sec_poly);
printf("1st Number: ");
display_poly(first_poly);
printf("2nd Number: ");
display_poly(sec_poly);
poly = (struct Node*)malloc(sizeof(struct Node));
add_poly(first_poly, sec_poly, poly);
printf("Added polynomial: ");
display_poly(poly);
return 0;
}
Output :
1st Number: 5x^2 +4x^1 + 2x^0
2nd Number: -5x^1 - 5x^0
Added polynomial: 5x^2 - 1x^1 -3x^0
Time Complexity :
The time complexity of the program would be O(a+b)O(a+b), where a will be the Number of nodes in the first linked list and b will be the Number of nodes in the second linked list since we are traversing both lists at once.
Addition of Long Positive Integer Using Linked List
In most programming languages, there is always a limit on the maximum value of an integer that it can store. But sometimes, there might be cases where we need to add two numbers, and the resultant number exceeds the limit of the integer.
We can do this by representing the numbers in the form of a linked list and then performing the addition on the linked list and storing the result into the resultant linked list.
To perform addition, we traverse both the linked lists parallelly, and then we add the corresponding digits and carry obtained from the previous edition, and we store that value in the resultant linked list.
For example, suppose we want to add two numbers : 543467 and 48315.
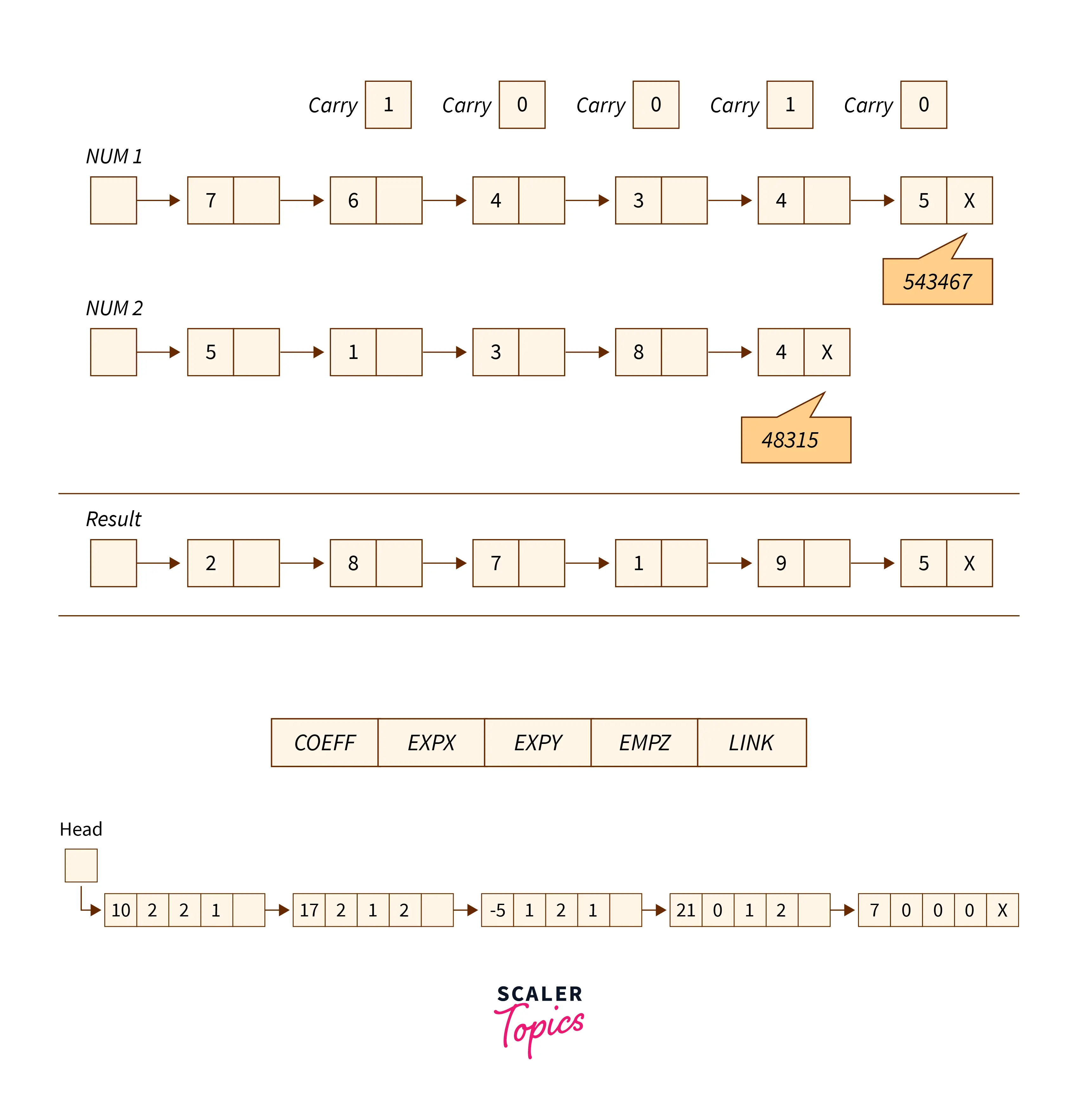
C++ program for the addition of two polynomials using Linked Lists :
#include <bits/stdc++.h>
using namespace std;
// node structure
class Node {
public:
int value;
Node* nxt;
};
// create new node
Node* create_node(int value){
Node* new_node = new Node();
new_node->value = value;
new_node->nxt = NULL;
return new_node;
}
//add a new node to a linked list
void add_node(Node** head_ref, int new_value){
Node* new_node = create_node(new_value);
new_node->nxt = (*head_ref);
(*head_ref) = new_node;
}
// function to add two linked lists
Node* add_list(Node* first, Node* second){
// head of result list
Node* res = NULL;
Node *temp, *prev = NULL;
int cry = 0, sum;
while (first != NULL || second != NULL) {
// sum will be the addition of carrying, first
//node and second node if they exist
sum = cry + (first ? first->value : 0) + (second ? second->value : 0);
// update carry is sum is greater than 10
cry = (sum >= 10) ? 1 : 0;
// update sum if the sum is greater than 10
sum = sum % 10;
temp = create_node(sum);
if (res == NULL)
res = temp;
else
prev->nxt = temp;
prev = temp;
if (first)
first = first->nxt;
if (second)
second = second->nxt;
}
if (cry > 0)
temp->nxt = create_node(cry);
return res;
}
// function to reverse the list
Node* reverse_list(Node* head){
if (head == NULL || head->nxt == NULL)
return head;
Node* rest = reverse_list(head->nxt);
head->nxt->nxt = head;
head->nxt = NULL;
return rest;
}
// function to print list
void printList(Node* node){
while (node != NULL) {
cout << node->value;
node = node->nxt;
}
cout << endl;
}
// main function
int main(void){
Node* res = NULL;
Node* first = NULL;
Node* second = NULL;
add_node(&first, 7);
add_node(&first, 6);
add_node(&first, 4);
add_node(&first, 3);
add_node(&first, 4);
add_node(&first, 5);
printf("First List is ");
printList(first);
add_node(&second, 5);
add_node(&second, 1);
add_node(&second, 3);
add_node(&second, 8);
add_node(&second, 4);
cout << "Second List is ";
printList(second);
first = reverse_list(first);
second = reverse_list(second);
res = add_list(first, second);
res = reverse_list(res);
cout << "Resultant list is ";
printList(res);
return 0;
}
Output :
First List is 543467
The Second List is 48315
The resultant list is 591782
Time Complexity :
The time complexity of the program would be O(a+b)O(a+b), where a will be the Number of nodes in the first linked list and b will be the Number of nodes in the second linked list since we are traversing both lists at once.
Polynomial of Multiple Variables
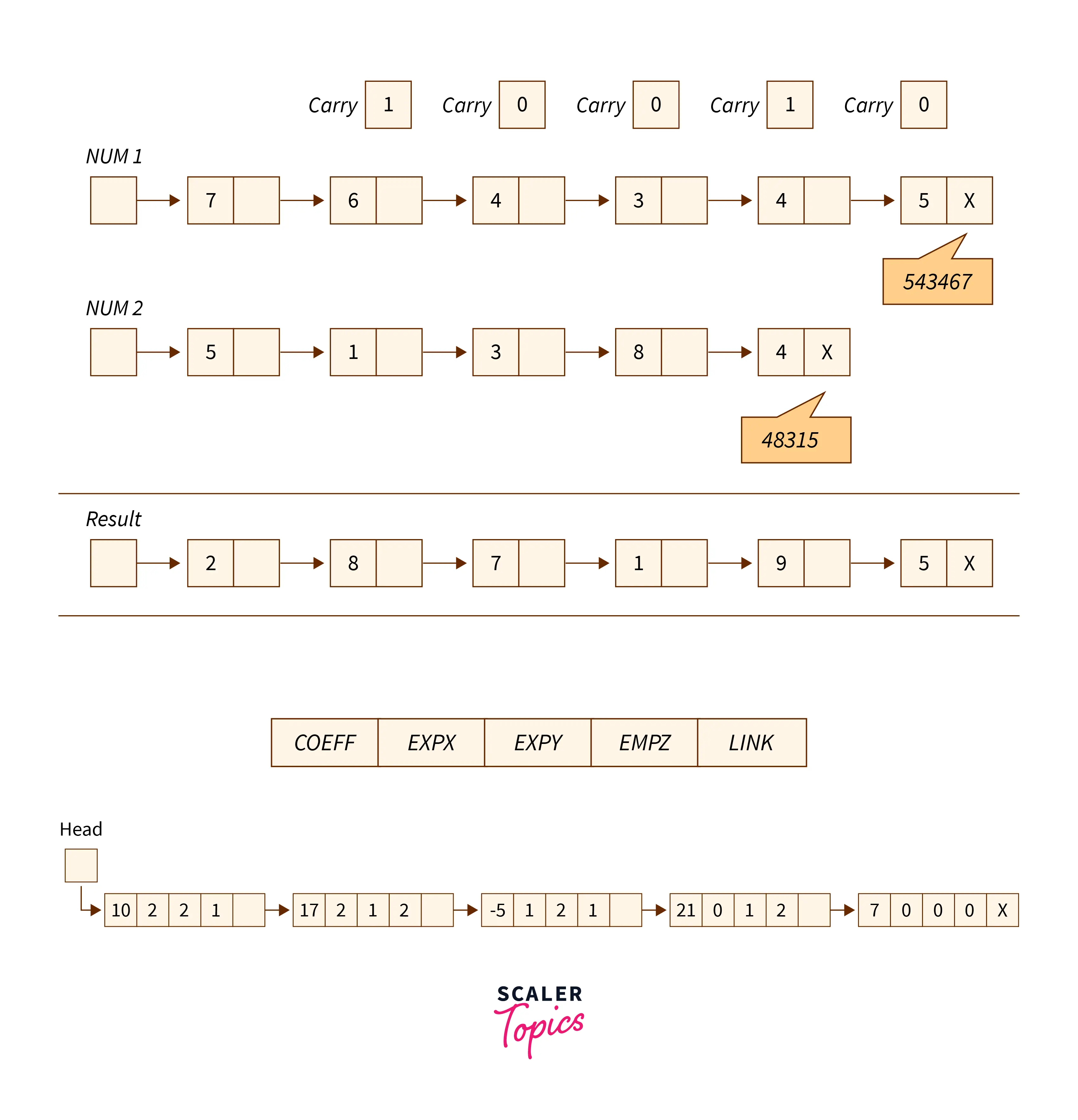
In polynomials, we can have more than one variable. Such polynomials can also be represented using a linked list in the same manner. In the case of multiple variables, each node of the linked list contains a separate part for each exponent. That is, if there are three variables, then there will be three parts for exponents.

Suppose we have polynomial $10x^2 y^2 z + 17 x^2y z^2 – 5 xy^2*z+ 21 y^4 z^2 + 7$.
It can be represented as a linked list :
Simple C++ program to multiply two polynomials :
To multiply two polynomials that are given in the form of an array, we simply traverse the first polynomial and multiply its every term with each term of the second polynomial.
#include <iostream>
using namespace std;
// array P contains coefficients of the first poly
// array Q contains coefficients of the second poly
int *mul(int P[], int Q[], int a, int n){
int *product = new int[a+n-1];
// product array
for (int i = 0; i<a+n-1; i++)
product[i] = 0;
// multiplication of two polynomials
for (int i=0; i<a; i++){
for (int j=0; j<n; j++)
product[i+j] += P[i]*Q[j];
}
return product;
}
// Function to print polynomial
void poly_print(int pol[], int n){
for (int i=0; i<n; i++){
cout << pol[i];
if (i != 0)
cout << "x^" << i ;
if (i != n-1)
cout << " + ";
}
}
// main function
int main(){
int P[] = {5, 0, 10, 6};
int Q[] = {1, 2, 4};
int a = sizeof(P)/sizeof(P[0]);
int n = sizeof(Q)/sizeof(Q[0]);
cout << "First polynomial is "<<endl;
poly_print(P, a);
cout<<endl;
cout << "Second polynomial is "<<endl;
poly_print(Q, n);
cout<<endl;
int *product = mul(P, Q, a, n);
cout << "Product polynomial is "<<endl;
poly_print(product, a+n-1);
return 0;
}
Output :
The first polynomial is
5 + 0x^1 + 10x^2 + 6x^3
The second polynomial is
1 + 2x^1 + 4x^2
Product polynomial is
5 + 10x^1 + 30x^2 + 26x^3 + 52x^4 + 24x^5
Time Complexity :
The time complexity of the given program will be O(a∗b), where a is the size of the first array and b is the size of the second array.
Some Other Applications of Linked List
Some important applications of a linked list include :
- Allocation of Memory
- Email applications
- Reducing file sizes on disk
- Implementation of advanced data structures
Advantages of Linked List Over Arrays
A few advantages of linked lists over arrays are :
- Dynamic size
- Efficient implementation of data structures
- No memory wastage
- Efficient insertion and deletion operation
Learn More
After reading this article, you might be getting curious to learn more about linked lists, or there might be some topics that you did not understand. To learn more about the linked list, you can refer to other articles present on Scaler topics on Linked list.
Conclusion
So far, we have discussed a lot about linked lists and their applications.
A few important points that we covered are :
- Linked lists have many applications both in computer science and in the real world.
- Some computer science applications include polynomial manipulations, implementation of advanced data structures, etc.
- Few real-world applications include web browsers, back buttons, music players, image viewers, etc.
- We can perform operations like addition, multiplication, etc. on polynomials with the help of linked lists.