The Uniform Cost Search Algorithm is a search algorithm to find the minimum cumulative cost of the path from the source node to the destination node. It is an uninformed algorithm i.e. it doesn’t have prior information about the path or nodes and that is why it is a brute-force approach.
What is the Uniform Cost Search Algorithm?
Uniform-Cost Search is a variation of Dijikstra’s algorithm. It is used to find the minimum path from the source node to the destination node around a directed weighted graph. This searching algorithm uses a brute force approach, visits all the nodes based on their current weight, and finds the path having minimum cost by repeatedly checking all the possible paths.
As it doesn’t consider any prior state or information about the path or the destination node, it is an uninformed search algorithm.
We use a boolean array visited and a priority queue to find the minimum cost. The node with minimum cost has the highest priority. It uses blind search as there is no prior information on the nodes.
The algorithm for the above algorithm is given as below:
- Create a priority queue, a boolean array visited of the size of the number of nodes, and a min_cost variable initialized with maximum value. Add the source node to the queue and mark it visited.
- Pop the element with the highest priority from the queue. If the removed node is the destination node, check the min_cost variable, if the value of the min_cost variable is greater than the current cost then update the variable.
- If the given node is not the destination node then add all the unvisited nodes to the priority queue adjacent to the current node.
Example
Input: Let the graph be as below with source node being A and destination E.
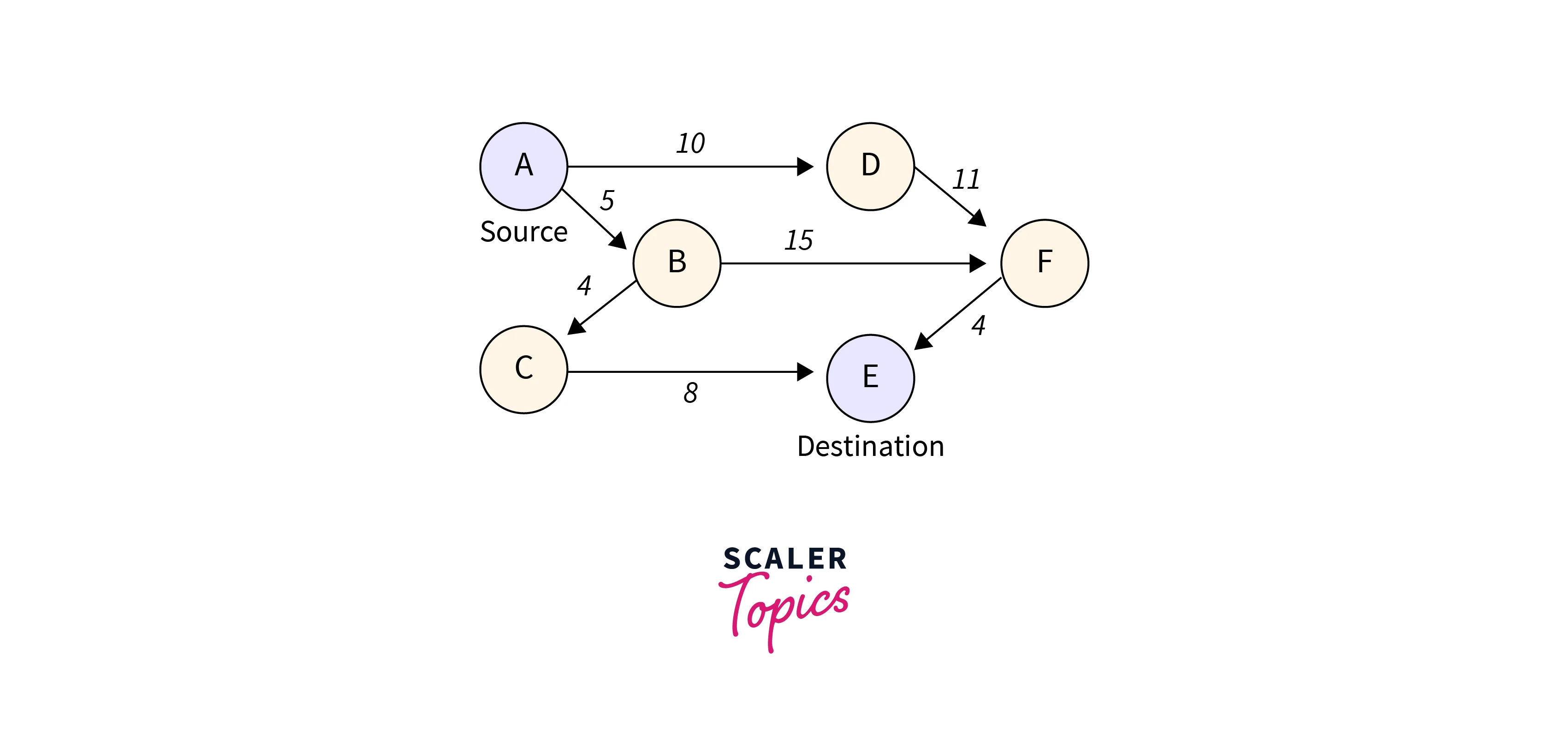
Output: 17
The shortest path here is A−>B−>C−>E forming the cost 17.
Let us apply the Uniform search Algorithm to this example:
We will have an empty priority queue and a boolean visited array. We will insert A with cost 0 into the queue.
Queue:
| A – 0 |
|---|
visited:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| False | False | False | False | False | False |
Step 1:
- Pop A from the queue.
- A is not destination node.
- Cost of A = 0, cst = 0.
- Append B and D to the queue with the costs cst + 10 and cst + 5.
- And mark A as visited.
Queue:
| B – 5 | D – 10 |
|---|
visited:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| True | False | False | False | False | False |
Step 2:
- Pop B from the Queue. As the cost of B is less than D, it appears first in the queue.
- B is not the destination node.
- Cost of B = 5, cst = 5.
- We will append C with cost 4 + cst and F with cost 15 + cst to the queue.
- Mark B as visited.
Queue:
| C – 9 | D – 10 | F – 20 |
|---|
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| True | True | False | False | False | False |
Step 3:
- Similarly, C is popped, and E is pushed in the stack.
- Similarly, D is popped, and F is pushed into the stack as it is still not visited.
Queue:
| E – 17 | F – 20 | F – 21 |
|---|
visited:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| True | True | True | True | False | False |
Step 4:
- Pop E from the Queue. As the cost of E is least it appears first in the queue.
- E is the destination node.
- Cost of E = 17, cst = 17.
- The initial value of min_cost is Infinity or Integer.MAX_VALUE. Thus, min_cost = cst = 17 is updated.
- We also don’t push any adjacent nodes.
- As E is the destination node we don’t mark it visited.
Queue:
| F – 20 | F – 21 |
|---|
visited:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| True | True | True | True | True | False |
Step 5:
- Pop F from the Queue.
- F is not the destination node.
- Cost of F = 20, cst = 20.
- F has the outgoing edge to E. We will push it to the queue with the cost 4 + cst.
- Mark F as visited.
Queue:
| F – 21 | E – 24 |
|---|
visited:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| True | True | True | True | False | True |
Step 6:
- Pop F from the Queue.
- F is not the destination node.
- Cost of F = 21, cst = 21.
- F has the outgoing edge to E. We will push it to the queue with the cost 4 + cst.
- Mark F as visited.
Queue:
| E – 24 | E – 25 |
|---|
visited:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| True | True | True | True | False | True |
Step 7:
- Pop E from the Queue.
- E is the destination node.
- Cost of E = 24 cst = 24.
- The min_cost = 17 and the current cost is 24. Thus, we are not required to update any values.
- Again Pop E from the Queue.
- The min_cost = 17 and the current cost is 25. Thus, we are not required to update any values.
- As the queue is now empty and the value of min_cost is not infinity, we found the node and now we will print the value in the output.
Implementation of Uniform Cost Search Algorithm
import java.util.PriorityQueue;
import java.util.*;
public class UniformCostSearch {
private static final int INF = Integer.MAX_VALUE;
/**
* Finds the shortest path from the source vertex to the destination vertex in the given graph.
*
* @param edges The edges of the graph.
* @param n The number of vertices in the graph.
* @param source The source vertex.
* @param destination The destination vertex.
* @return The minimum cost of the shortest path.
*/
public static int findShortestPath(int[][] edges, int n, int source, int destination) {
// Create a priority queue to store the nodes to be expanded.
// The priority queue is sorted in ascending order of the cost of the nodes.
PriorityQueue<Node> queue = new PriorityQueue<>((a, b) -> a.cost - b.cost);
// Initialize the visited array.
boolean[] visited = new boolean[n];
// Create a graph.
// The graph is represented as a hash map, where the key is the vertex and the value is a set of adjacent nodes.
HashMap<Integer, HashSet<Node>> graph = new HashMap<>();
for (int i = 0; i < n; i++) {
graph.put(i, new HashSet<Node>());
}
for (int i = 0; i < edges.length; i++) {
graph.get(edges[i][0]).add(new Node(edges[i][1], edges[i][2]));
}
// Create a node for the source vertex.
Node startNode = new Node(source, 0);
// Add the source vertex to the queue.
queue.add(startNode);
// Initialize the minimum cost to infinity.
int minCost = INF;
while (!queue.isEmpty()) {
// Get the node with the minimum cost from the queue.
Node curNode = queue.poll();
int cst = curNode.cost;
// If the current node is the destination, then we have found the shortest path.
if (curNode.vertex == destination) {
minCost = Math.min(minCost, cst);
} else {
// Mark the current node as visited.
visited[curNode.vertex] = true;
// Iterate over the adjacent nodes of the current node.
for (Node neighbor : graph.get(curNode.vertex)) {
// If the neighbor is not visited, then add it to the queue with the updated cost.
if (!visited[neighbor.vertex]) {
queue.add(new Node(neighbor.vertex, neighbor.cost + cst));
}
}
}
}
return minCost;
}
/**
* A node in the graph.
*/
private static class Node implements Comparable<Node> {
int vertex;
int cost;
/**
* Creates a new node with the given vertex and cost.
*
* @param vertex The vertex of the node.
* @param cost The cost of the node.
*/
public Node(int vertex, int cost) {
this.vertex = vertex;
this.cost = cost;
}
@Override
public int compareTo(Node other) {
return this.cost - other.cost;
}
}
public static void main(String[] args) {
// Create the graph.
int[][] graph = new int[][]{
{0, 3, 10},
{0, 1, 5},
{1, 5, 15},
{1, 2, 4},
{2, 4, 8},
{3,5,11},
{5,4,4}
};
// The source vertex.
int source = 0;
// The destination vertex.
int destination = 4;
// Find the shortest path from the source vertex to the destination vertex.
int minCost = UniformCostSearch.findShortestPath(graph, 6, source, destination);
Output:
The minimum cost is 17
Explanation: We are given an array that contains a list of edges and its cost. We create a graph in the form of a hashmap. Next, we push all the directed edges to the graph.
Now, we create a visited boolean array and a priority queue. We pop the node with the highest priority from the queue i.e. having the least cost. If the current node is the destination node then we simply update the cost if the current cost is minimum. Otherwise, we add the non-visited adjacent nodes to the queue.
Time Complexity
Time Complexity: $$ O(b^(1 + C / ε)) $$
- b: The branching factor, representing the maximum number of successors for any node.
- C: The cost of the optimal solution.
- ε: The minimum cost between any two states.
The Uniform Cost Search algorithm explores nodes in a way that prioritizes nodes with the lowest accumulated cost so far. The algorithm’s time complexity is exponential in the ratio of C to ε. If ε is relatively large as compared to C then the time complexity is reasonable. However, if the value of ε is smaller compared to C then the time complexity of the algorithm increases and may become impractical.
FAQs
Q. What is the space complexity of the algorithm?
A. The space complexity of the algorithm is O(|V|), where |V| is the number of vertices in the graph. This is because the algorithm needs to store a queue of size |V| to keep track of the nodes to be expanded.
Q. What are the disadvantages of the algorithm?
It can be slow for graphs with a large number of vertices and edges.
It does not work for graphs with negative weights.
Q. What are the advantages of the algorithm?
It is simple to implement.
It is efficient, with a time complexity of $$ O(b^(1 + C / ε))$$
It is guaranteed to find the shortest path from the source vertex to the destination vertex.
Conclusion
- Uniform Cost Search (UCS) Algorithm is a searching algorithm that is a variation of Dijikstra’s algorithm.
- It is used to find the minimum cost between 2 nodes and is a brute-force approach. We use Priority Queue and a boolean visited array.
- The time complexity of the algorithm is $$ O(b^(1 + C / ε)) $$ where b is the branching factor, c is the cost of optimal cost, and ε is the cost between any two states.