Unbounded Knapsack

Problem Statement

Given a knapsack weight W and a set of N items with certain values(benefit or profit) val, and weights wt, find the maximum amount that could make up the exact knapsack weight.
In Unbounded Knapsack, you may select an item multiple times.

Example

N = 4

W = 10

val[] = {15, 25, 20, 10}

wt[] = {3, 4, 6, 8}

Example Explanation

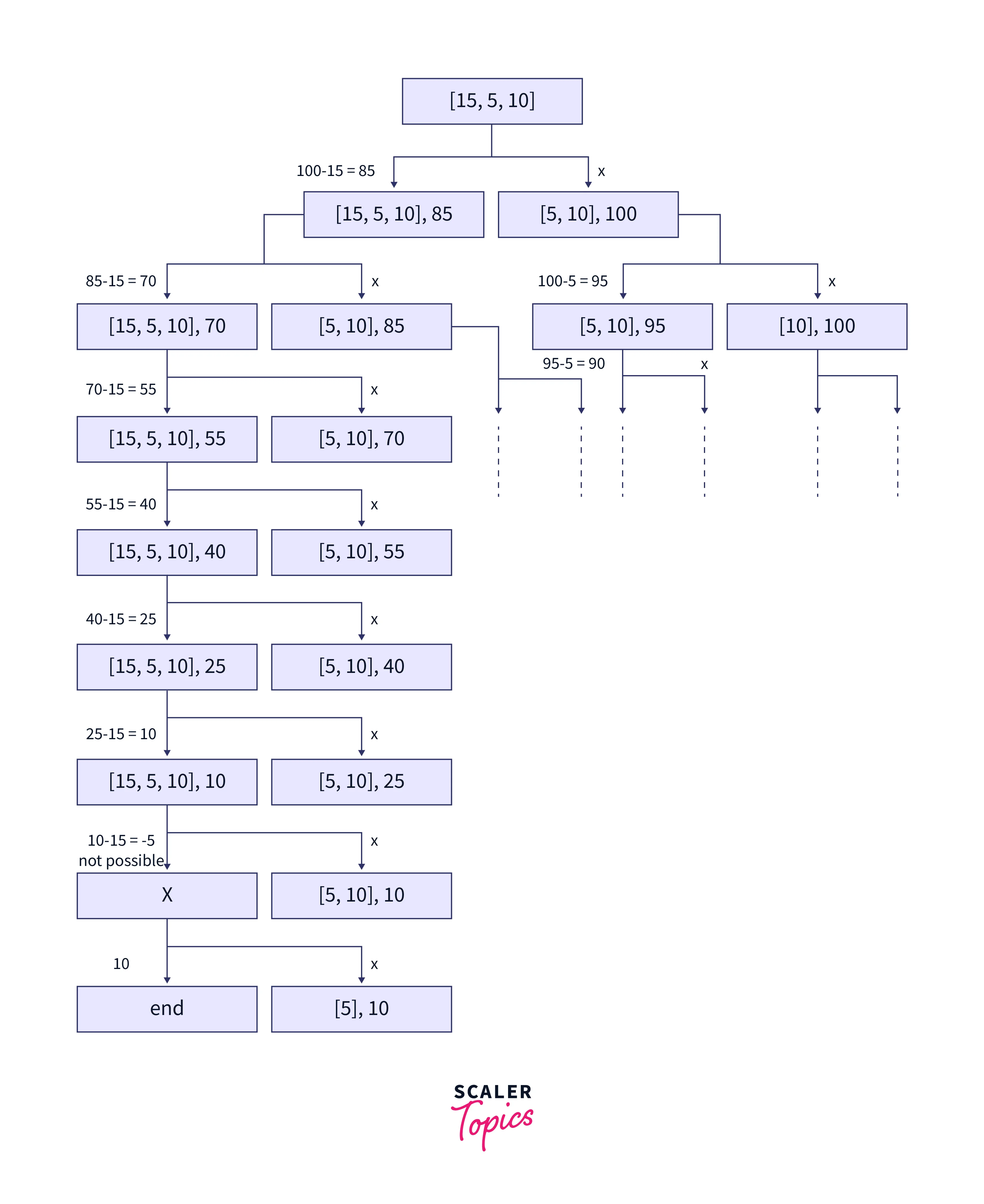
Therefore to get the best outcome the selected items are :
Item number 2, with weight 4 yields a profit of 25.
Item number 1, with weight 3 yields a profit of 15.
Item number 1, with weight 3 yields a profit of 15.

Therefore total profit using the unbounded knapsack will be $25+15+15 = 55$.

Input/Output

Input

• The first line of input integer N represents the number of items.
• The second line contains an array val of length N that contains values of the items.
• The third line contains an array wt of length N that contains the weights of the items.
• The fourth line contains the integer W which represents the total weight of the knapsack.

Output

The first and only line of the output contains an integer that represents the maximum profit that can be obtained without crossing the weight limit of the knapsack.

Constraints

$1 ~≤ ~N~,~ W ~≤ ~1000$
$1 ~≤ ~val[i]~, ~wt[i] ~≤ ~100$

Algorithm 1 – Brute Force Approach – Recursive Approach

Algorithm

• Step 1 – Begin by calling the recursive function ‘unboundedKnapsack()’ that takes parameters W, index, val, and wt.
• Step 2 – Set the base case that if ‘index’ = 0 or ‘W’ = 0 function returns 0.
• Step 3 – Next, check if the weight of the item at the index is more than the knapsack weight ‘W’.
  • If yes then return the result obtained after recursively calling the ‘unboundedKnapsack()’ function for the remaining elements.
  • Else using the max function return the maximum of the following
    • result obtained by calling the recursive function ‘getMaxVal()’ for ‘index – 1’ and ‘W – weight[index]’.
    • result obtained by calling the recursive function ‘unboundedKnapsack()’ for ‘index - 1’ items with ‘W’ weight.

Code Implementation

C++

/* Java program to find maximum profit with an unbounded knapsack of weight W.*/
#include<iostream>
#include<algorithm>
using namespace std; 
/* Recursive function of unbounded Knapsack problem to return maximum value with knapsack capacity (without using any extra space)*/
static int unboundedKnapsack(int W, int index, int val[], int wt[]){
    /*  Base case of recursion with only one item.*/
    if (index == 0) {
        return (W / wt[0]) * val[0];
    }
    /* If the wt of an item at index is more than W it cannot be included.  */
    if (wt[index] > W){
        return unboundedKnapsack(W, index - 1, val, wt);
    }
    /* Case 1: Solution does not include the item at the index */
    int item_not_included = 0 + unboundedKnapsack(W,index-1,val,wt);
    /* Case 2: Item at index is included in solution */
    int item_included = val[index] + unboundedKnapsack(W-wt[index],index,val,wt);
    /*return maximum of the above cases*/
    return max(item_included,item_not_included);
}
// Driver code
int main(){
    int N, i, W;
    cout<<"Enter the number of items: "; 
    cin>>N;  
    int val[N], wt[N]; 
    cout<<"Enter value of the items: "; 
    for(i=0; i<N; i++){
        cin>>val[i];} 
    cout<<"Enter weight of the items: "; 
    for(i=0; i<N; i++){
        cin>>wt[i];}
    cout<<"Enter the weight of the knapsack: "; 
    cin>>W;  
    cout<<"The maximum profit that can be obtained is : ";
    cout<<unboundedKnapsack(W, N-1, val, wt);
}

Java

/* Java program to find maximum profit with an unbounded knapsack of weight W.*/
import java.io.*;
import java.util.*; 
class Main {
    /* Function to return a maximum of two integers */
    static int max(int a, int b){ 
        if(a>b)
            {return a;}
        else
            {return b;}
    }
    /* Recursive function of unbounded Knapsack problem to return maximum value with knapsack capacity (without using any extra space)*/
    static int unboundedKnapsack(int W, int index, int val[], int wt[]){
        /*  Base case of recursion with only one item.*/
        if (index == 0) {
            return (W / wt[0]) * val[0];
        }
        /* If the wt of an item at index is more than W it cannot be included.  */
        if (wt[index] > W){
            return unboundedKnapsack(W, index - 1, val, wt);
        }
        /* Case 1: Solution does not include the item at the index */
        int item_not_included = 0 + unboundedKnapsack(W,index-1,val,wt);
        /* Case 2: Item at index is included in solution */
        int item_included = val[index] + unboundedKnapsack(W-wt[index],index,val,wt);
        /*return maximum of the above cases*/
        return max(item_included,item_not_included);
    }

    // Driver code
    public static void main(String args[]){
        int N, i, W;  
        Scanner sc=new Scanner(System.in);  
        System.out.print("Enter the number of items: ");  
        N=sc.nextInt();  
        int[] val = new int[N];  
        System.out.print("Enter value of the items: ");  
        for(i=0; i<N; i++){
            val[i]=sc.nextInt();}
        int[] wt = new int[N];  
        System.out.print("Enter weight of the items: ");  
        for(i=0; i<N; i++){
            wt[i]=sc.nextInt();}
        System.out.print("Enter the weight of the knapsack: ");  
        W=sc.nextInt();  
        System.out.print("The maximum profit that can be obtained is : ");
        System.out.println(unboundedKnapsack(W, N-1, val, wt));
    }
}

Python

# Python program to find maximum profit with an unbounded knapsack of weight W.
# Recursive function of unbounded Knapsack problem to return maximum value with a knapsack capacity (without using any extra space)
def unboundedKnapsack(W, index, val, wt):
    #Base case of recursion with only one item.
    if index==0 :
        return (W//wt[0])*val[0]
    # If the wt of an item at index is more than W it cannot be included.        
    if (wt[index] > W):
        return unboundedKnapsack(W, index - 1, val, wt)
    # Case 1: Solution does not include the item at the index
    item_not_included=0+unboundedKnapsack(W,index-1,val,wt)
    # Case 2: Item at the index is included in the solution
    item_included=val[index]+unboundedKnapsack(W-wt[index],index,val,wt)
    # return a maximum of the above cases
    return max(item_included,item_not_included)

# Driver program
if __name__ == '__main__':
    N = int(input("Enter the number of items: "))
    val = list(map (int, input ("Enter value of the items: ").split ()))
    wt = list(map (int, input ("Enter weight of the items: ").split ()))
    W = int(input("Enter the weight of the knapsack: "))
    print("The maximum profit that can be obtained is :", end=" ")
    print(unboundedKnapsack(W, N-1, val, wt))

Output

Enter the number of items: 4
Enter value of the items: 15 25 20 10
Enter weight of the items: 3 4 6 8
Enter the weight of the knapsack: 90 
The maximum profit that can be obtained is : 55

Time Complexity

The recursive calls increase at a rate of 2 until ‘N’ or ‘W’ becomes 0, as every function calls itself twice.
Thus the maximum possible calls are $2^N$. The overall time complexity for this approach will be $O(2^N)$.

Space Complexity

The recursive approach is based on calculating the total weight and value of all subsets without using any additional data structure. Since no extra space is required the space complexity for this approach will be O(1).

Algorithm 2 – Bottom-Up Approach – Dynamic Programming – Iteration + Tabulation

Algorithm

• Step 1 – Initialize a 2D array ‘dp’ of size $(N + 1) * (W)$ and fill it with -1.
• Step 2 – Call the recursive function ‘unboundedKnapsack()’ that takes parameters W, N, val, and wt.
• Step 3 – To find the maximum profit for every sub-array and every possible Knapsack Weight use dp as a table where:
  • Either exclude the item and consider profit obtained from the sub-array excluding it dp[i - 1][j].
  • Or include the item if weight is lesser than the knapsack weight available val[i] + dp[i][j - wt[i]] and consider the maximum of the two.

Code Implementation

C++

/* CPP program to find maximum profit with an unbounded knapsack of weight W.*/
#include <bits/stdc++.h>
using namespace std;

/* function of unbounded Knapsack problem to return maximum value with knapsack capacity*/
int unboundedKnapsack(int W, int N, int val[], int wt[]){
    vector<vector<int> > dp(N, vector<int>(W + 1, -1));
    int i=0,j=0;
    /*  Get the values for the considered item for every capacity */
    for(i=1; i<=W; i++)
        dp[0][i] = ((i / wt[0]) * val[0]);
    /* For each item, check for every possible weight*/
    for(i=1; i<N; i++){
        for(j=1; j<W+1; j++){
            if (wt[i] <= j)
                dp[i][j] = max(dp[i - 1][j], val[i] + dp[i][j - wt[i]]);
            else
                dp[i][j] = dp[i - 1][j];
        }
    }
    return dp[N-1][W];
}

// Driver code
int main(){
    int N, i, W;
    cout<<"Enter the number of items: "; 
    cin>>N;  
    int val[N], wt[N]; 
    cout<<"Enter value of the items: "; 
    for(i=0; i<N; i++){
        cin>>val[i];} 
    cout<<"Enter weight of the items: "; 
    for(i=0; i<N; i++){
        cin>>wt[i];}
    cout<<"Enter the weight of the knapsack: "; 
    cin>>W;  
    cout<<"The maximum profit that can be obtained is : ";
    cout<<unboundedKnapsack(W, N-1, val, wt);
    return 0;
}

Java

/* Java program to find maximum profit with an unbounded knapsack of weight W.*/
import java.io.*;
import java.util.*;

class Main {
    /*Function that returns a maximum of two integers */
    static int max(int a, int b) { 
        if(a>b)
            {return a;}
        else
            {return b;}
        }

    /* function of unbounded Knapsack problem to return maximum value with knapsack capacity*/
    static int unboundedKnapsack(int W, int N, int val[], int wt[]){
        int[][] dp = new int[N][W + 1];
        for (int row[] : dp)
            Arrays.fill(row, -1);
        int i=0,j=0;
        /*  Get the values for the considered item for every weight */
        for(i=1; i<=W; i++){
            dp[0][i] = ((i / wt[0]) * val[0]);
        }
        /* For each item, check for every possible weight */
        for(i=1; i<N; i++){
            for(j=1; j<W+1; j++){
                if (wt[i] <= j){
                    dp[i][j] = max(dp[i - 1][j], val[i] + dp[i][j - wt[i]]);
                }
                else{
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[N-1][W];
    }

    // Driver code
    public static void main(String args[]){
        int N, i, W;  
        Scanner sc=new Scanner(System.in);  
        System.out.print("Enter the number of items: ");  
        N=sc.nextInt();  
        int[] val = new int[N];  
        System.out.print("Enter value of the items: ");  
        for(i=0; i<N; i++){
            val[i]=sc.nextInt();}
        int[] wt = new int[N];  
        System.out.print("Enter weight of the items: ");  
        for(i=0; i<N; i++){
            wt[i]=sc.nextInt();}
        System.out.print("Enter the weight of the knapsack: ");  
        W=sc.nextInt();  
        System.out.print("The maximum profit that can be obtained is : ");
        System.out.println(unboundedKnapsack(W, N, val, wt));
    }
}

Python

"""Python program to find maximum profit with an unbounded knapsack of weight W."""
# function of unbounded Knapsack problem to return maximum value with a knapsack capacity
def unboundedKnapsack(W, N, val, wt):
    row = [0] * (W + 1)
    dp = [row] * N
    # Get the values for the considered item for every capacity
    for i in range(W + 1):
        dp[0][i] = (i // wt[0]) * val[0]
    # For each item, check for every possible weight or capacity
    for i in range(1, N):
        for j in range(1, W + 1):
            if (wt[i] <= j):
                dp[i][j] = max(dp[i - 1][j], val[i] + dp[i][j - wt[i]])
            else:
                dp[i][j] = dp[i - 1][j]
    return dp[i][j]

# Driver program
if __name__ == '__main__':
    N = int(input("Enter the number of items: "))
    val = list(map (int, input ("Enter value of the items: ").split ()))
    wt = list(map (int, input ("Enter weight of the items: ").split ()))
    W = int(input("Enter the weight of the knapsack: "))
    print("The maximum profit that can be obtained is :", end=" ")
    print(int(unboundedKnapsack(W, N, val, wt)))

Output

Enter the number of items: 4
Enter value of the items: 15 25 20 10
Enter weight of the items: 3 4 6 8
Enter the weight of the knapsack: 10
The maximum profit that can be obtained is : 55

Time Complexity

Since N * W subproblems are considered the overall time complexity for this approach will be O(N * W).

Space Complexity

As a new 2D array ‘dp’ is being introduced,
Therefore, the overall space complexity for this approach will be O(N * W).

Algorithm 3 – Top-down Approach – Dynamic Programming with Memoization

Algorithm

The top-down approach aims at removing duplicate calls by using an array to store the state of ‘N’ and ‘W’.

• Step 1- Initialize a 2D array ‘dp’ of size $(N + 1) * (W)$ and fill it with -1.
• Step 2 – Call the recursive function ‘unboundedKnapsack()’ that takes parameters W, index, val, wt, and dp.
• Step 3 – Set the base case that if ‘index’ = 0 or ‘W’ = 0 function returns 0.
• Step 4- Next, check if the value is present in the array. If yes, then return the value.
• Step 5 – Next, check if the weight of the item at the index is more than the knapsack weight ‘W’.
  • If yes then return the result obtained after recursively calling the ‘unboundedKnapsack()’ function for the remaining elements.
  • Else return the maximum of the following
    • result obtained by calling the recursive function ‘getMaxVal()’ for ‘index - 1’ and ‘W - weight[index]’.
    • result obtained by calling the recursive function ‘unboundedKnapsack()’ for ‘index - 1’ items with ‘W’ weight.

Code Implementation

C++

/* CPP program to find maximum profit with an unbounded knapsack of weight W.*/
#include <bits/stdc++.h>
using namespace std;

/* function of unbounded Knapsack problem to return maximum value with knapsack capacity*/
int unboundedKnapsack(int W, int index, int val[], int wt[], vector<vector<int> >& dp){
    /*  Base case of recursion with only one item.*/
    if (index == 0)
        return (W / wt[0]) * val[0];
    /* Return if the value is pre-calculated */
    if (dp[index][W] != -1)
        return dp[index][W];
    /* If the wt of an item at index is more than W it cannot be included.  */
    if (wt[index] > W)
        return unboundedKnapsack(W, index - 1, val, wt, dp);
    /* Case 1: Solution does not include the item at the index */
    int item_not_included = unboundedKnapsack(W, index-1, val, wt, dp);
    /* Case 2: Item at index is included in solution */
    int item_included = val[index] + unboundedKnapsack(W-wt[index], index, val, wt, dp);
    /*return maximum of the above cases*/
    return dp[index][W] = max(item_included, item_not_included);
}

// Driver code
int main(){
    int N, i, W;
    cout<<"Enter the number of items: "; 
    cin>>N;  
    int val[N], wt[N]; 
    cout<<"Enter value of the items: "; 
    for(i=0; i<N; i++){
        cin>>val[i];} 
    cout<<"Enter weight of the items: "; 
    for(i=0; i<N; i++){
        cin>>wt[i];}
    cout<<"Enter the weight of the knapsack: "; 
    cin>>W;  
    cout<<"The maximum profit that can be obtained is : ";
    /* Introducing 2D array dp. */
    vector<vector<int> > dp(N, vector<int>(W + 1, -1));
    cout<<unboundedKnapsack(W, N-1, val, wt, dp);
    return 0;
}

Java

/* Java program to find maximum profit with an unbounded knapsack of weight W.*/
import java.io.*;
import java.util.*;

class Main {
    /*Function that returns a maximum of two integers */
    static int max(int a, int b) { 
        if(a>b)
            {return a;}
        else
            {return b;}
        }

    /* function of unbounded Knapsack problem to return maximum value with knapsack capacity*/
    static int unboundedKnapsack(int W, int index, int val[], int wt[], int dp[][]){
        /*     Base case of recursion with only one item.*/
        if (index == 0){
            return (W / wt[0]) * val[0];}
        /* Return if the value is pre-calculated */
        if (dp[index][W] != -1){
            return dp[index][W];}
        /* If the wt of an item at index is more than W it cannot be included.  */
        if (wt[index] > W){
            return unboundedKnapsack(W, index - 1, val, wt, dp);}
        /* Case 1: Solution does not include the item at the index */
        int item_not_included = unboundedKnapsack(W, index-1, val, wt, dp);
        /* Case 2: Item at index is included in solution */
        int item_included = val[index] + unboundedKnapsack(W-wt[index], index, val, wt, dp);
        /*return maximum of the above cases*/
        return dp[index][W] = max(item_included, item_not_included);
    }

    // Driver code
    public static void main(String args[]){
        int N, i, W;  
        Scanner sc=new Scanner(System.in);  
        System.out.print("Enter the number of items: ");  
        N=sc.nextInt();  
        int[] val = new int[N];  
        System.out.print("Enter value of the items: ");  
        for(i=0; i<N; i++){
            val[i]=sc.nextInt();}
        int[] wt = new int[N];  
        System.out.print("Enter weight of the items: ");  
        for(i=0; i<N; i++){
            wt[i]=sc.nextInt();}
        System.out.print("Enter the weight of the knapsack: ");  
        W=sc.nextInt();  
        System.out.print("The maximum profit that can be obtained is : ");
        /* Introducing 2D array dp.*/
        int[][] dp = new int[N][W + 1];
        for (int row[] : dp)
            Arrays.fill(row, -1);
        System.out.println(unboundedKnapsack(W, N-1, val, wt, dp));
    }
}

Python

"""Python program to find maximum profit with an unbounded knapsack of weight W."""

#function of unbounded Knapsack problem to return maximum value with a knapsack capacity
def unboundedKnapsack( W, index, val, wt, dp):
    #   Base case of recursion with only one item.
    if (index == 0):
        return (W // wt[0]) * val[0];
    #Return if the value is pre-calculated 
    if (dp[index][W] != -1):
        return dp[index][W];
    # If the wt of an item at index is more than W it cannot be included.  
    if (wt[index] > W):
        return unboundedKnapsack(W, index - 1, val, wt, dp)
    # Case 1: Solution does not include the item at the index 
    item_not_included = unboundedKnapsack(W, index-1, val, wt, dp)
    # Case 2: Item at the index is included in the solution 
    item_included = val[index] + unboundedKnapsack(W-wt[index], index, val, wt, dp)
    #return a maximum of the above cases
    dp[index][W] = max(item_included, item_not_included)
    return dp[index][W]


# Driver program
if __name__ == '__main__':
    N = int(input("Enter the number of items: "))
    val = list(map (int, input ("Enter value of the items: ").split ()))
    wt = list(map (int, input ("Enter weight of the items: ").split ()))
    W = int(input("Enter the weight of the knapsack: "))
    print("The maximum profit that can be obtained is :", end=" ")
    # Introducing 2D array dp.
    row = [-1]*(W + 1)
    dp = [row]*N
    print(int(unboundedKnapsack(W, N-1, val, wt, dp)))

Output

Enter the number of items: 4
Enter the value of the items: 15 25 20 10
Enter the weight of the items: 3 4 6 8
Enter the weight of the knapsack: 10
The maximum profit that can be obtained is : 55

Time Complexity

Since N * W recursive calls are made the overall time complexity for this approach will be O(N * W).

Space Complexity

As a new 2D array ‘dp’ is being introduced, the space complexity will be O(N * W).
Again, O(N) space is required for the recursive call stack.
Therefore, the overall space complexity for this approach will be O(N * W) + O(N).

FAQ

Q. What is a Knapsack Problem?

A. A knapsack problem deals with a set of items that have some assigned weight and value. The main goal of the problem is to fill the knapsack with the maximum possible value within the given weight constraint.

Q What are the different knapsack problems?

A. There are 3 types of knapsack problems.
a) Fractional Knapsack
b) 0/1 Knapsack
c) Unbounded Knapsack

Q. What is the difference between a 0/1 knapsack and an unbounded knapsack?

A. The difference between 0/1 Knapsack and Unbounded Knapsack is that the latter allows the utilization of an infinite number of items.

Q. Name some problems related to unbounded knapsack?

A. Rod cutting, coin change, and maximum ribbon cut problems are related to the unbounded knapsack problem.

Conclusion

• The unbounded knapsack problem has no upper bound on the number of copies of each kind of item.
• Approach 1 – Trying all possible combinations of items and computing the maximum of those profits.
  • Time Complexity: $O(2^N)$
  • Space Complexity: $O(1)$
• Approach 2 – Using a 2D array, such that the last cell of dp stores the maximum value which can be achieved using all items and i capacity of the knapsack.
  • Time Complexity: $O(N * W)$
  • Space Complexity: $O(N * W)$
• Approach 3 – Using memory to return similar encounters from the array, instead of recomputing it.
  • Time Complexity: $O(N * W)$
  • Space Complexity: $O(N * W) + O(N)$