Types of Binary Tree

Binary trees are a fundamental data structure with various types. The two primary types of binary tree are full binary trees, where each node has either two children or no children, and complete binary trees, which are filled from left to right at each level. Additionally, there are balanced types of binary tree, such as AVL trees and red-black trees, that maintain a balance factor or color property to ensure efficient operations.

Introduction

A tree whose elements have at most two children is called a binary tree. The left element is called the left child and the right element is called the right child.

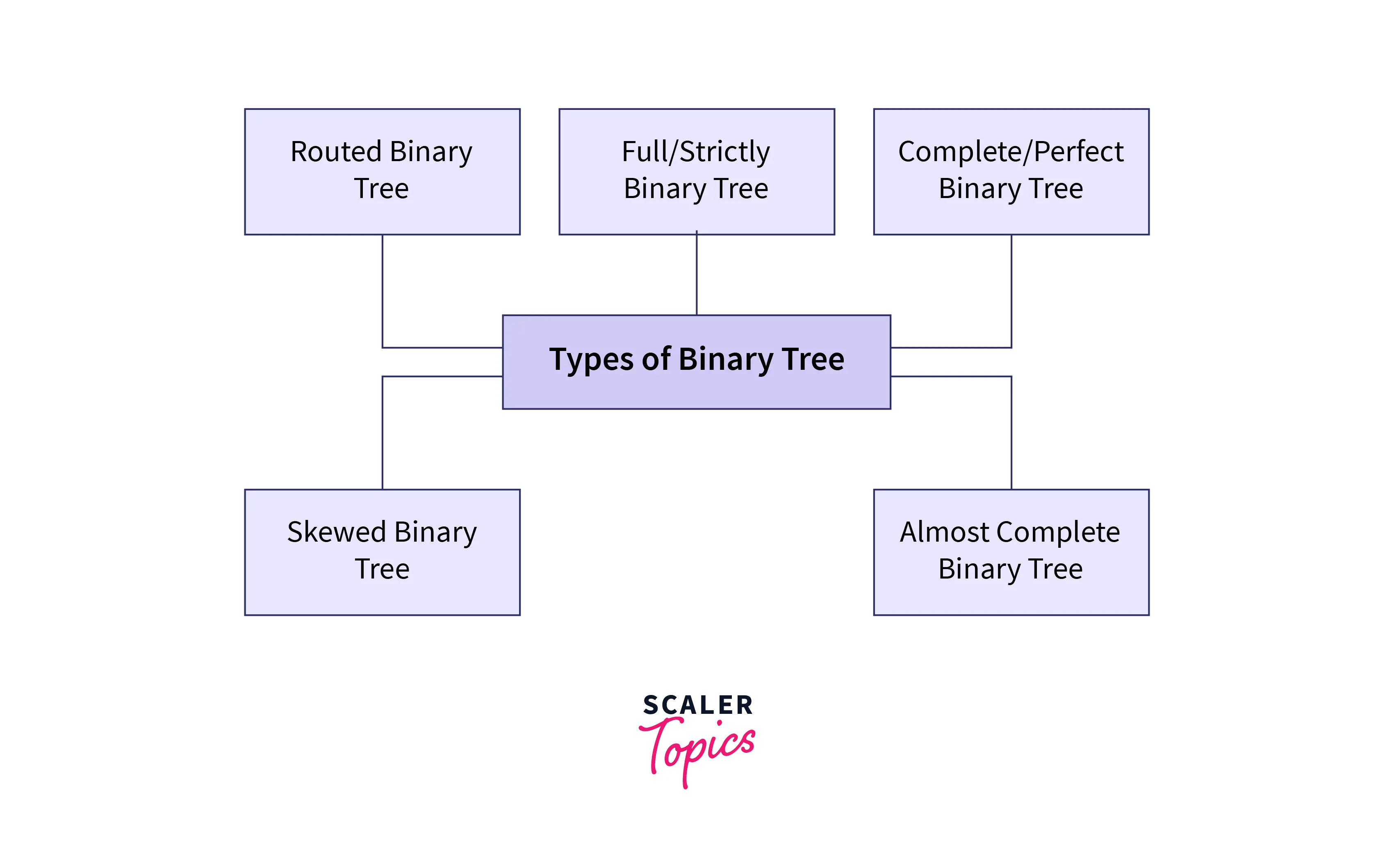
Based on the position of nodes and their unique features, following are Types of Binary Tree

• Rooted Binary Tree
• Full Binary Tree
• Perfect Binary Tree
• Complete Binary Tree
• Almost Complete Binary Tree
• Infinite Complete Binary Tree
• Degenerate or Pathological Tree
• Skewed Binary Tree
• Balanced Binary Tree
• Extended Binary Tree

What is a Binary tree?

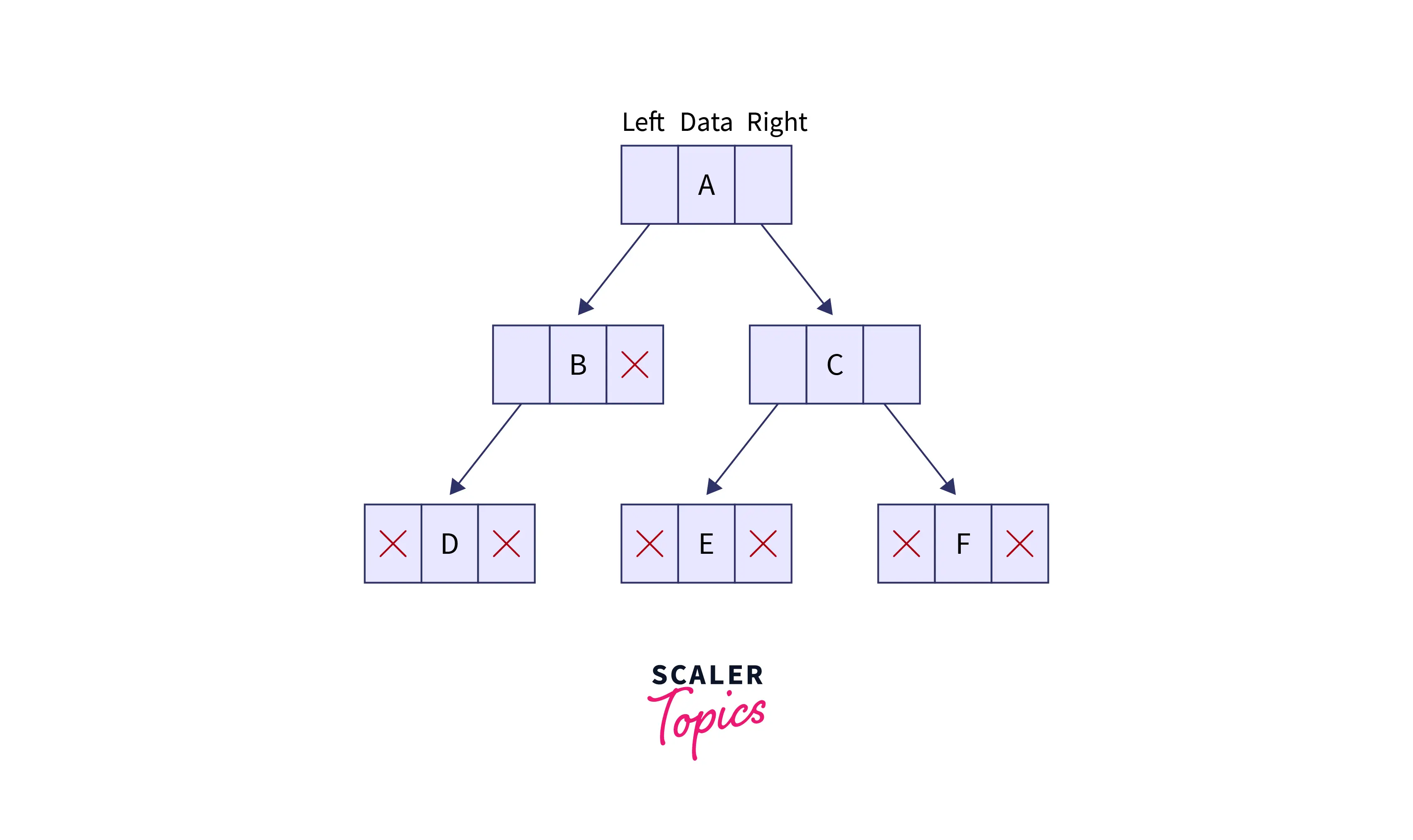
A binary tree is a tree-type data structure where each node has at most two children, referred to as the left child and the right child. Properties

1. A binary tree has a root node. If the root node has no children, it is called a NULL tree. The height of such a tree is 0.
2. Each node forms a binary tree itself.
3. A node can have at most two children.

The number of nodes in a full binary tree is at least 2h+1 and at most=$2^{h+1}$-1, where h is the height of the tree.

5. The maximum number of nodes at level ‘l’ of a binary tree is $2^l$.
6. In a non-empty binary tree, if n is the total number of nodes and E is the total number of edges, then E = n-1.

Terminologies Associated with Binary Tree and Types of Binary Tree

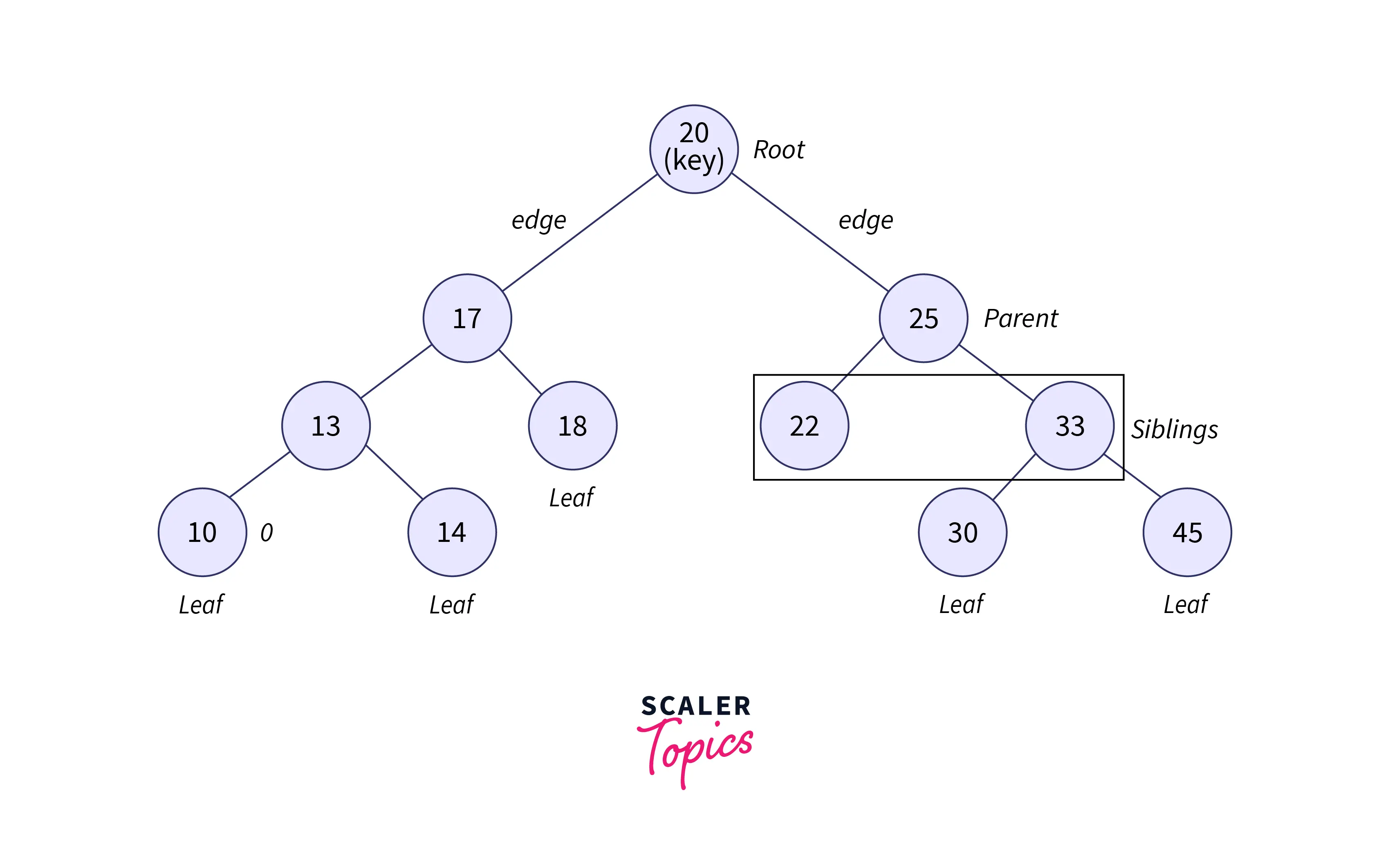
• Root: Topmost node in a tree is called the root.
• Node: The node is the termination point in a tree that contains all the data.
• Edge: Edge is the line that connects one node to another.
• Parent:A node that is connected by a directed edge to another node at its lower level is called a parent node.
• Child: The node to which the parent node is connected when moving towards the leaf nodes is the child node.
• Sibling Node: Two nodes present at the same level, having the same parents are called sibling nodes.
• Leaf/External Node: Leaf nodes are nodes with no children.
• Internal Node: Internal node is the node with at least one child.
• Depth of a Node: The number of edges from the root to a node is called the depth of that node.
• Height of a Node: The height of a node is the number of edges from the node to the deepest leaf.
• Height of Tree: The height of the tree is the maximum height of any node. The value is the same as the height of the root node.

Types of Binary tree

There are several types of binary tree:

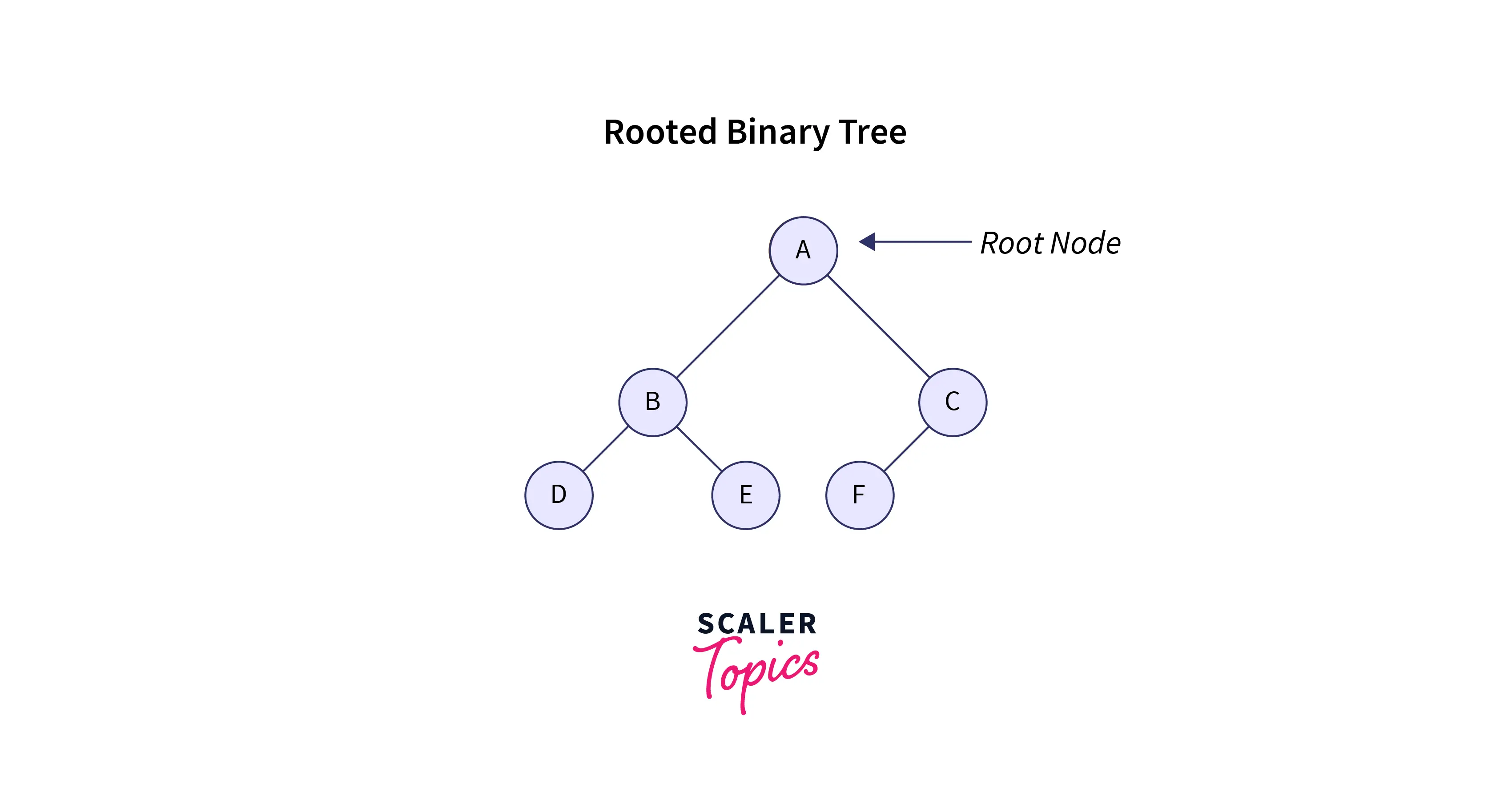
1. Rooted Binary Tree

A rooted binary tree has a root node, and every node has at most two children. A rooted binary tree is a connected acyclic graph that has a special node called the root of the tree and edges that originate directly or indirectly from the root.

2. Full Binary Tree

A full binary tree, also known as a proper binary tree, is a binary tree in which all non-leaf nodes have exactly two children. In other words, in a full binary tree, all nodes have either 0 or 2 children.

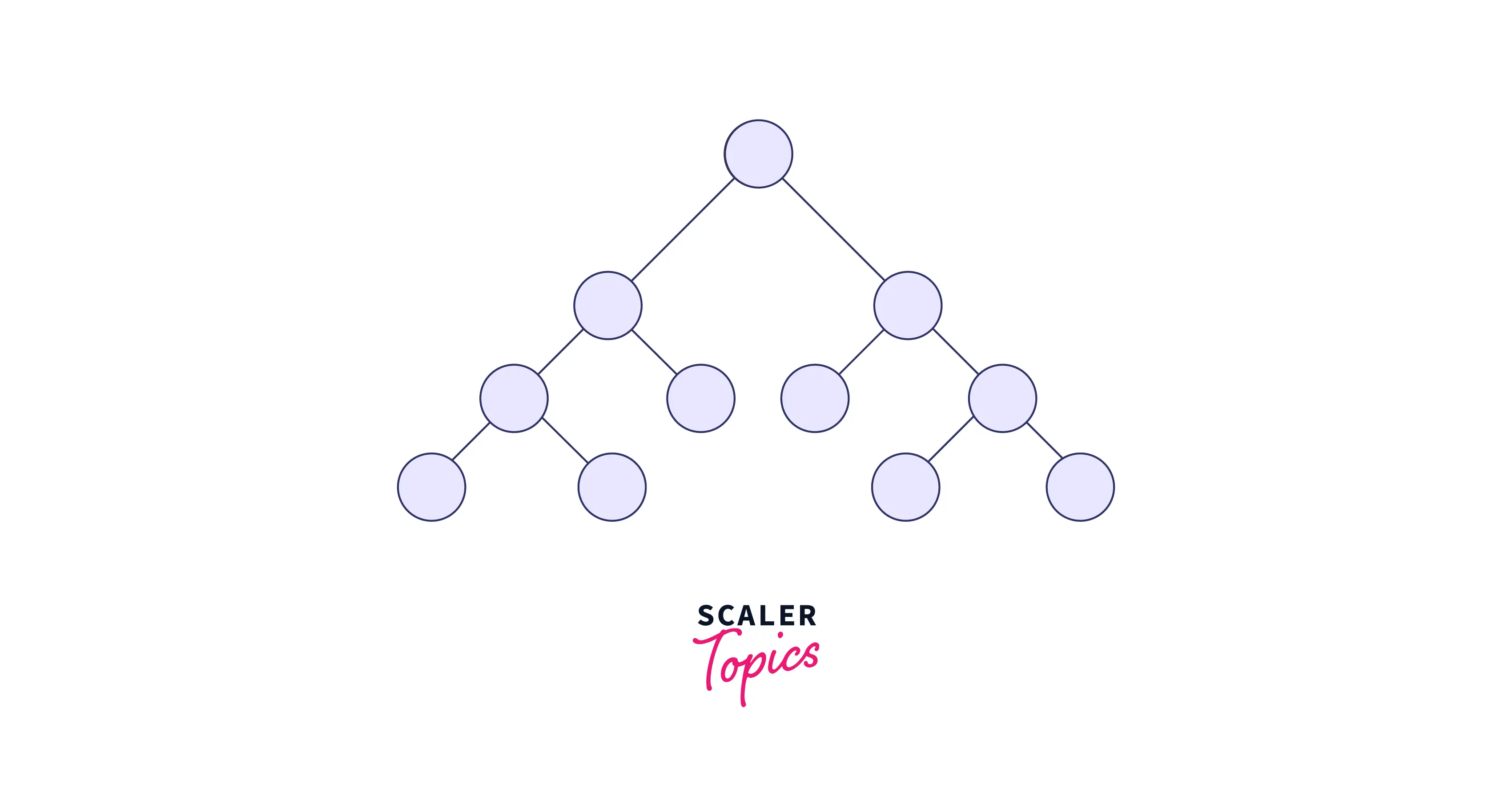
3. Perfect Binary Tree

In a perfect binary tree, all the internal nodes have exactly two children. Every leaf node in a perfect binary tree must be present at the same level. A perfect binary tree is also called a strict binary tree.

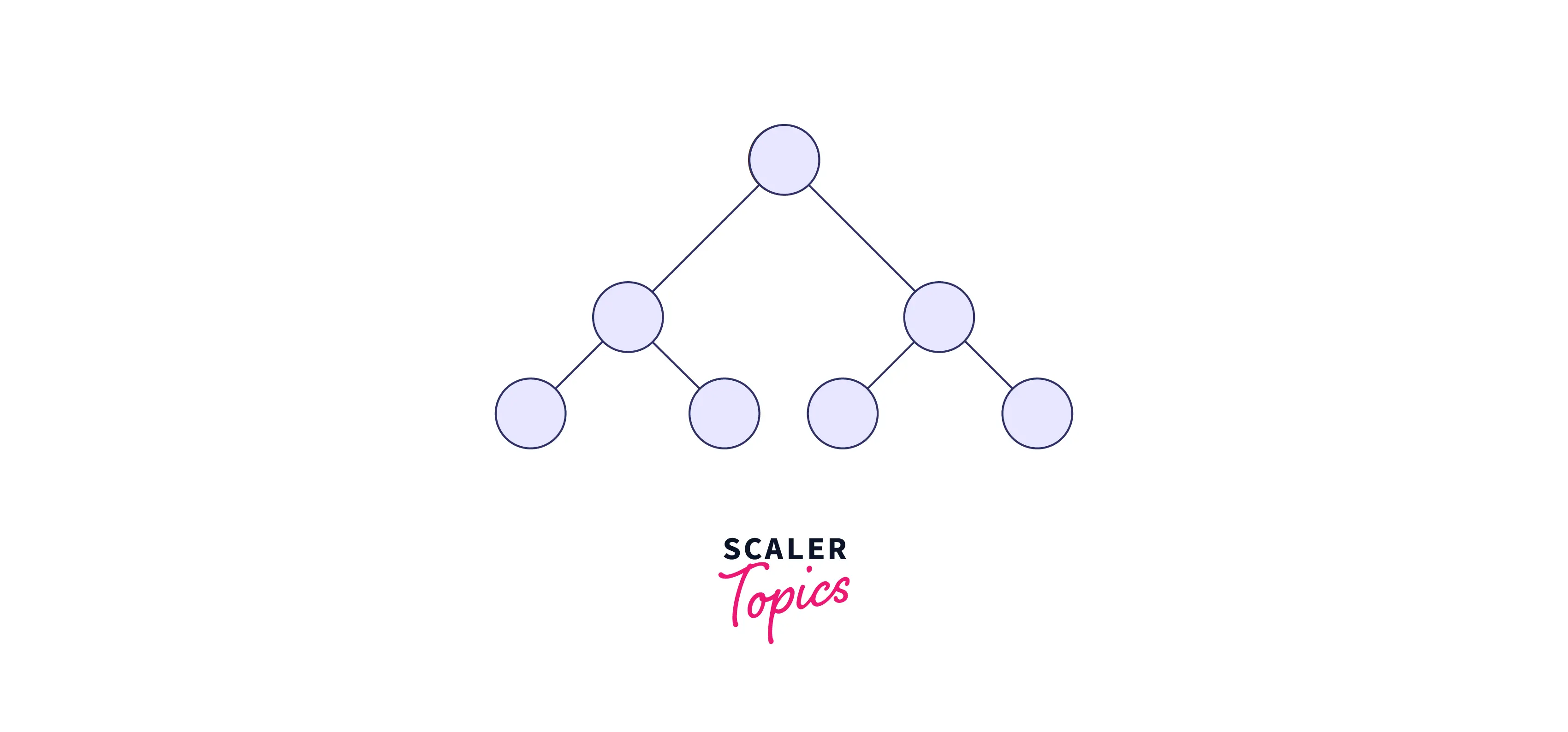
4. Complete Binary Tree

A complete binary tree is a binary tree in which node insertion takes place from the left.

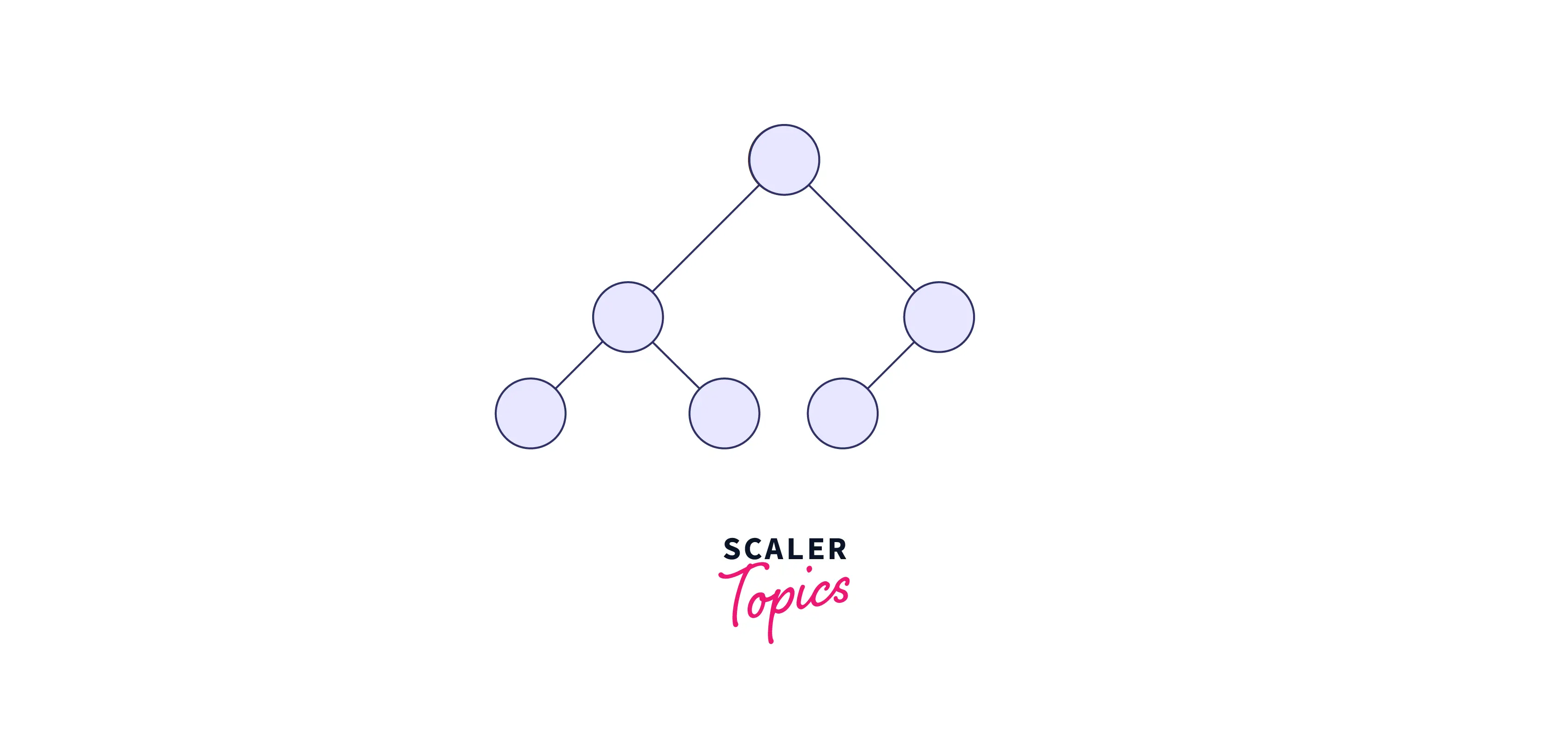
5. Almost Complete Binary Tree

A special kind of binary tree where insertion takes place level by level and from the left at each level. The last level may be partially or fully filled.

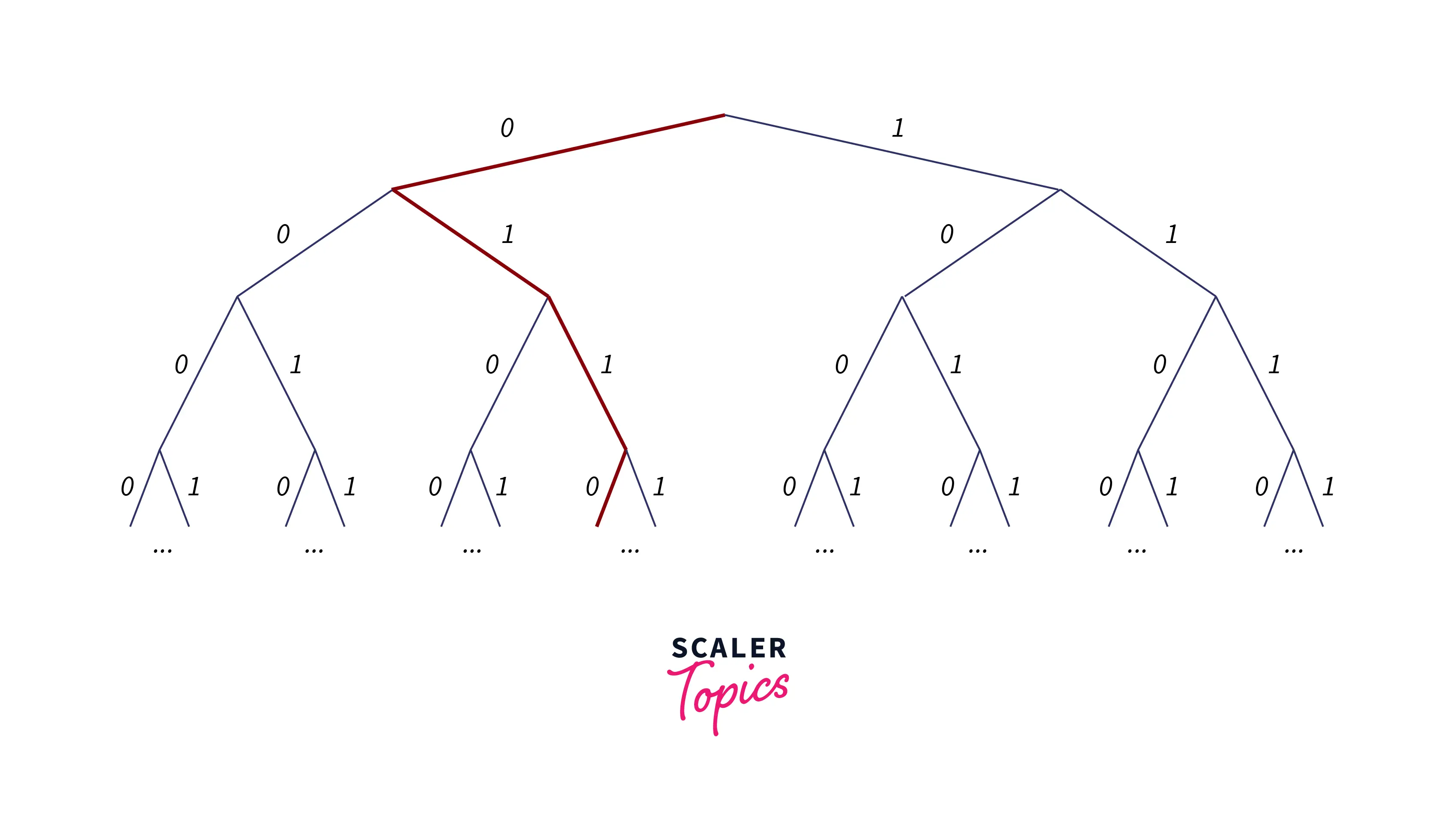
6. Infinite Complete Binary Tree

In an infinite complete binary tree, every node has two children. The set of all nodes is countably infinite while the set of all infinite paths from the root is uncountable.

7. Degenerate or Pathological Tree

A binary tree is degenerate or pathological if every non-leaf node has a single child.

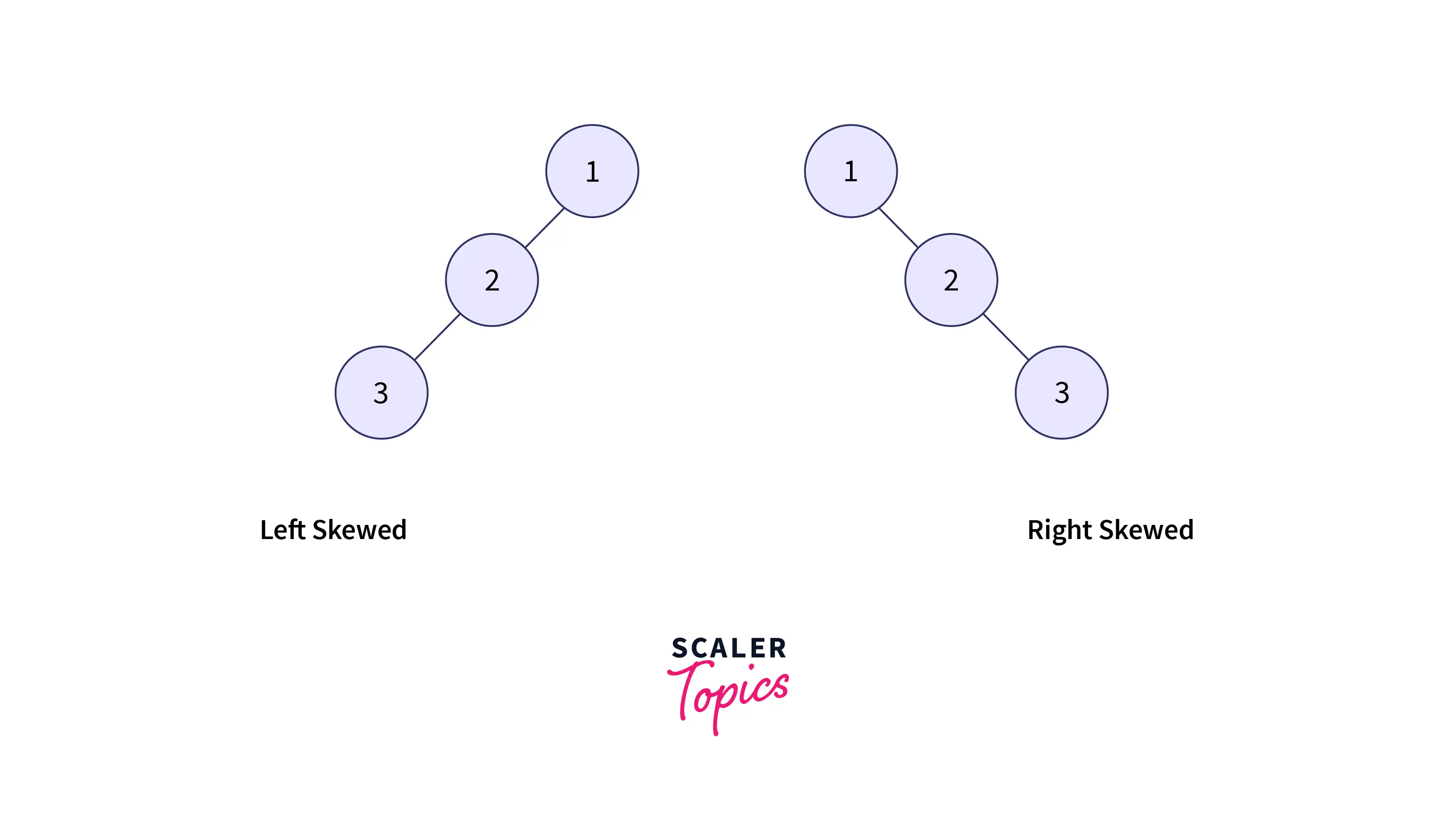
8. Skewed Binary Tree

The binary tree that is dominated either by the left child node or right child node is called a Skewed Binary Tree.
All non-leaf nodes in a skewed binary tree are associated with only one child.

• Left skewed tree – Binary tree with most nodes having a left child without a corresponding right child.
• Right skewed tree – Binary tree with most nodes having a right child without a corresponding left child.

9. Balanced Binary Tree

A balanced binary tree is a special kind of binary tree in which the height of the left and right subtrees of each node varies by at most one.
Balanced factor = height of left subtree – height of right subtree =-1, 0, or 1

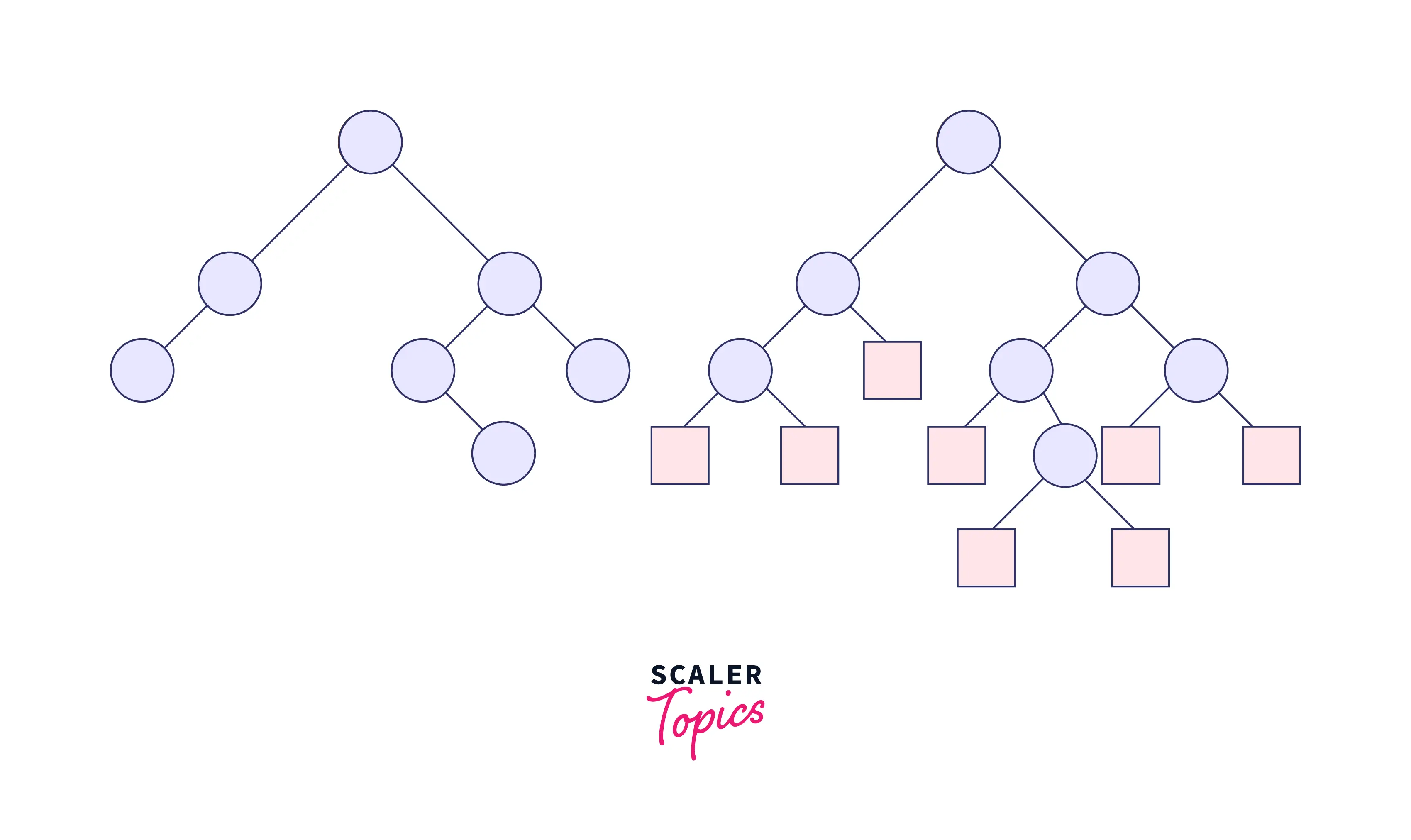
10. Extended Binary Tree

A binary tree is said to be extended when it replaces all its null subtrees with special nodes.

• The nodes from the original tree are internal nodes, and the special nodes are external nodes.
• In the extended binary tree, all the internal nodes have exactly two children, and the external nodes are leaf nodes.
  Thus the outcome appears to be a complete binary tree.
  
  

Some Special Types of Trees

1. AVL Trees

AVL trees are self-balancing binary search trees where the heights of the left and right subtrees of any node differ by at most one. This ensures efficient search, insertion, and deletion operations with a time complexity of O(log n), making them suitable for applications that require frequent modifications to the tree structure.

2. Red-Black Trees

Red-black trees are another type of self-balancing binary search tree. They maintain balance using a set of color properties assigned to each node. Red-black trees guarantee that the longest path from the root to a leaf is no more than twice the length of the shortest path, ensuring a balanced structure and efficient operations with a time complexity of O(log n).

3. B-trees

B-trees are self-balancing search trees designed to handle large amounts of data and disk-based storage. They are commonly used in file systems and databases. B-trees have a variable number of child nodes for each internal node, allowing for efficient disk access and minimizing the number of I/O operations required to access or modify data.

4. Trie (Prefix Tree)

A trie, also known as a prefix tree, is a specialized tree structure used for efficient retrieval of strings or words. It is particularly useful for tasks like prefix matching and autocomplete. Each node in a trie represents a common prefix, and the edges are labeled with individual characters. Tries offer fast lookup and insertion of words, typically with a time complexity of O(m), where m is the length of the word being searched or inserted.

5. Segment Trees

Segment trees are a data structure used for efficient range queries and updates on a sequence of elements. They are especially useful in scenarios involving problems like finding the sum, minimum, or maximum value within a given range. Segment trees provide an improved time complexity of O(log n) for most operations compared to naive approaches that have linear time complexity.
:::section{.main}

Learn more

• Binary Tree in Data Structure

Conclusion

• The binary tree is a non-linear tree-type data structure.
• Every node of a binary tree must have at most two children.
• A binary tree node contains the following parts.
  • Data
  • Pointer to left child
  • Pointer to the right child
• The search operation in a binary tree is faster than in other trees.