Before jumping into the traversal of binary tree algorithms, let’s define a Tree as a data structure first. That will help you to grasp the concepts in a more meaningful way.
The tree is a hierarchical data structure that is defined as a collection of nodes. In a tree, nodes represent the values and are connected by edges. A binary tree is a tree, in which each node can have at most two nodes. The top-most node is known as the root node, while the nodes with no children are known as leaf nodes.
Traversal of a tree means visiting and outputting the value of each node in a particular order. Trees are organized through relationships or hierarchies. This allows us to traverse them in multiple ways. Traversals are classified by the order in which the nodes are visited. We will study about traversal of binary tree in details ahead in the article.
Scope of the Article
- This article discusses about what is
binary treeand the traversal of binary tree in data structure - It also discusses about the inorder traversal of binary tree, preorder traversal of binary tree and the post order traversal of binary tree, stating their algorithms (or pseudocode) with relevant examples
- We will also analyze the time and space complexity for each of the traversals of binary tree, along with their applications
- This article, however, does not discuss the construction of the tree data structure from the scratch or the complete code in any particular language.
The overall article meets the above defined scope. With that being said, let us get started!
Takeaways
Binary tree traversals:
- Depth First Search (DFS)
- Breadth First Search (BFS)
Introduction
Trees are important not only in nature because they provide us oxygen to breathe, they are also a significant data structure that exists in computer science and solves our complex problems!

What are Binary Trees?
A binary tree is a tree-type non-linear data structure with a maximum of two children for each parent. Every node in a binary tree has a left and right reference along with the data element. The node at the top of the hierarchy of a tree is called the root node.
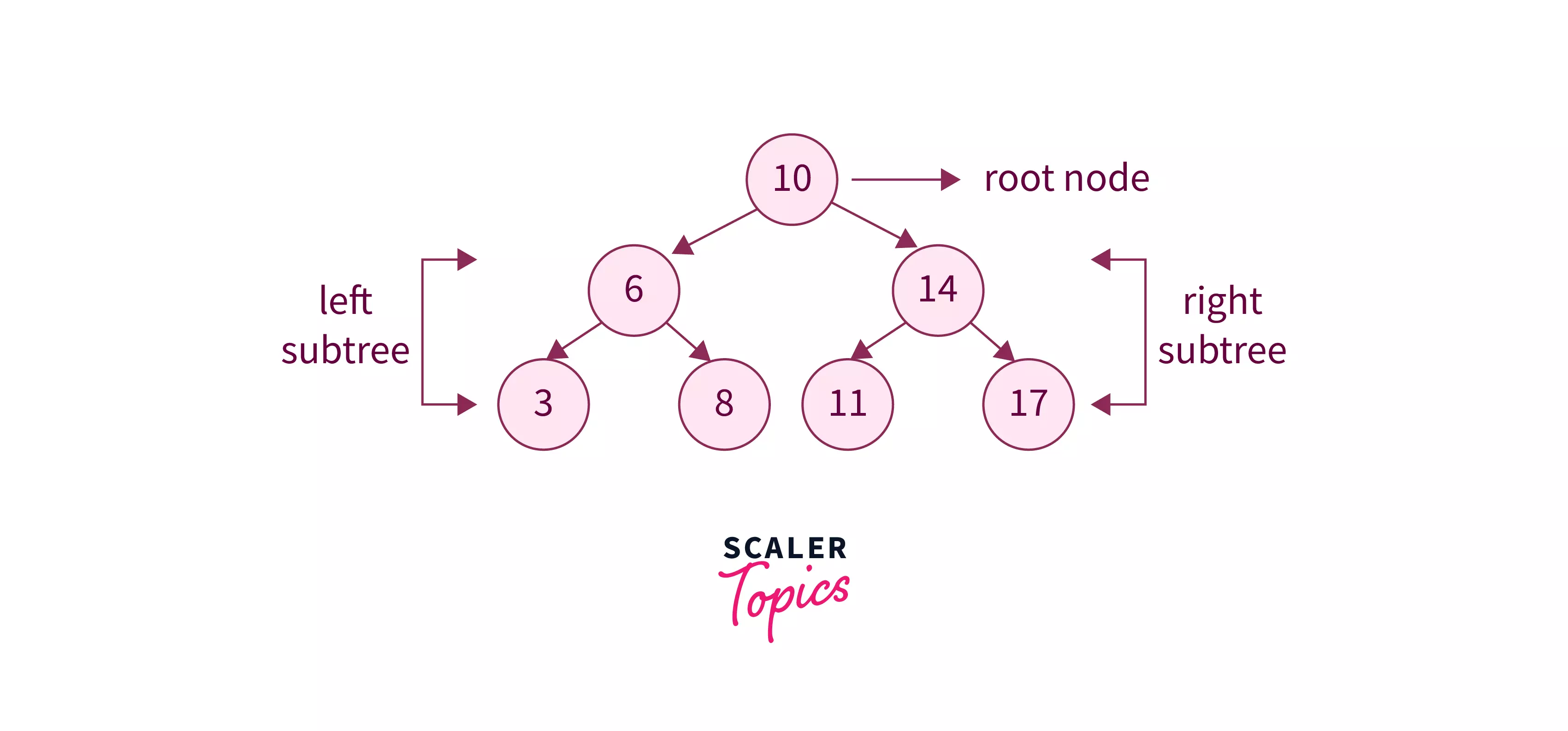
To learn more about binary trees, refer to Binary Tree in Data Structure.
What is Traversing?
Traversing is the process by which we can visit and access each and every element present in any data structure like an array, linked list, or tree. It is an operation which can be implemented on any data structure. Traversal is the most basic of the operations that can be performed on any data structure. In this article, we will learn about the traversal of binary tree.
What is Traversal of a Binary Tree?
In computer science, traversal of binary tree (also known as tree search) refers to the process of visiting (checking or updating) each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited. There are different ways ( and order ) of visiting a tree data structure.
We will know about the different types of traversal of a binary tree ahead.
Types of Binary Tree Traversal
Tree Traversal Algorithms can be classified broadly in the following two categories by the order in which the nodes are visited:
Depth First Search (DFS) Algorithm: Depth-First Search is an important algorithm for traversal of binary tree. It starts with the root node and first visits all nodes of one branch as deep as possible of the chosen Node and before backtracking, it visits all other branches in a similar fashion.
To traverse binary trees with depth-first search, the following operations are performed at each node:
- If the current node is empty, then simply return.
- Execute the following three operations in a particular order:
N: Visit the current node.L: Recursively traverse the current node’s left subtree.R: Recursively traverse the current node’s right subtree.
There are 3 tree traversals that are mostly based on the DFS. They are given below:
- Preorder Traversal
- Inorder Traversal
- Postorder Traversal
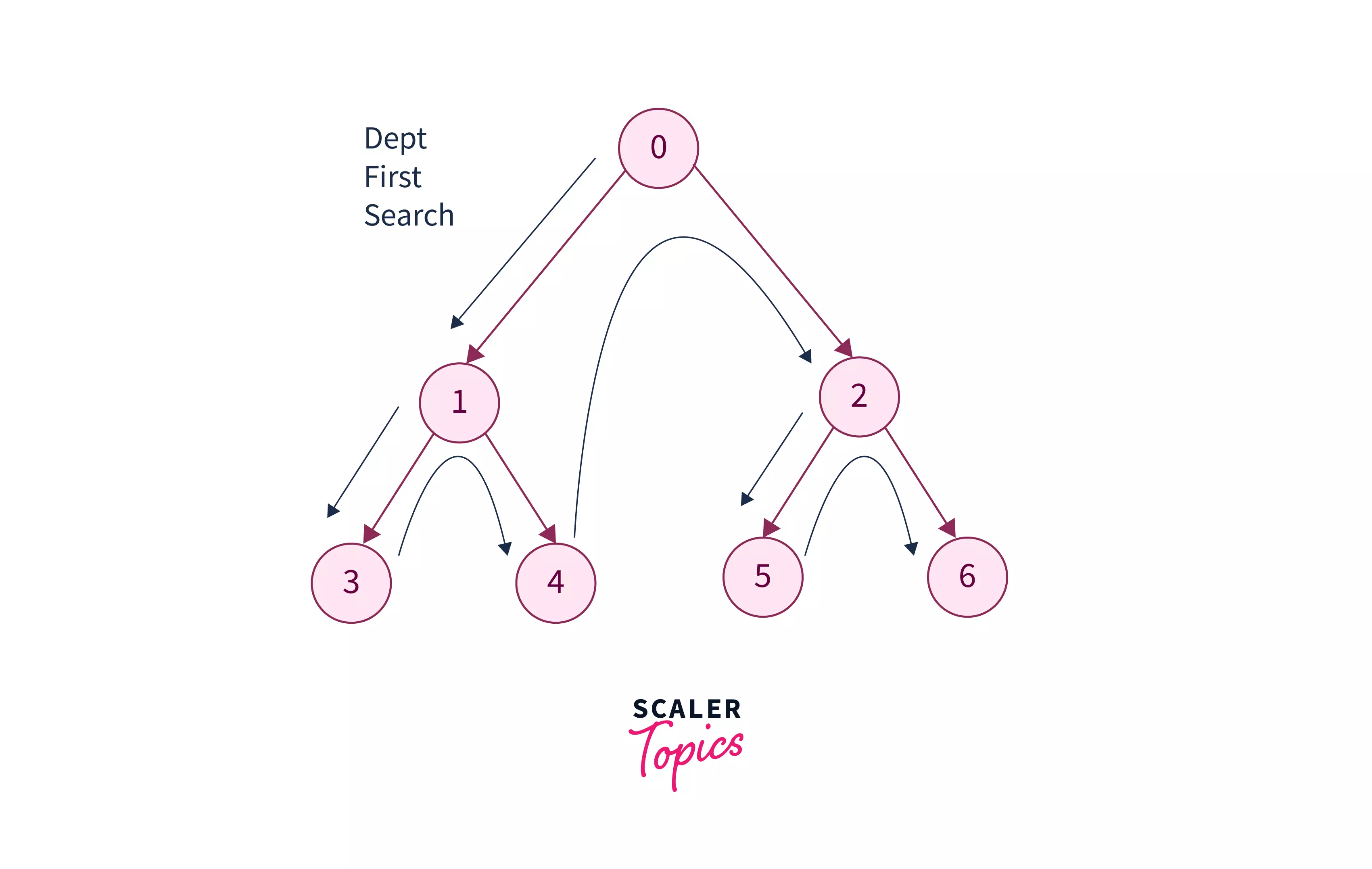
We will discuss all the above traversals ahead in our article, in depth.
Breadth First Search (BFS) Algorithm: Breadth First Search (BFS) Algorithm is also an important algorithm for traversal of binary tree. It starts from the root node and visits all nodes of the current depth before moving to the next depth in the tree. In simple words, BFS algorithm traverses the tree level by level and depth by depth. BFS uses the queue data structure in general. There is an algorithm, known as the level order traversal that follows the breadth first traversal for the tree traversal. However, level order traversal of binary tree is not under the scope of this article.
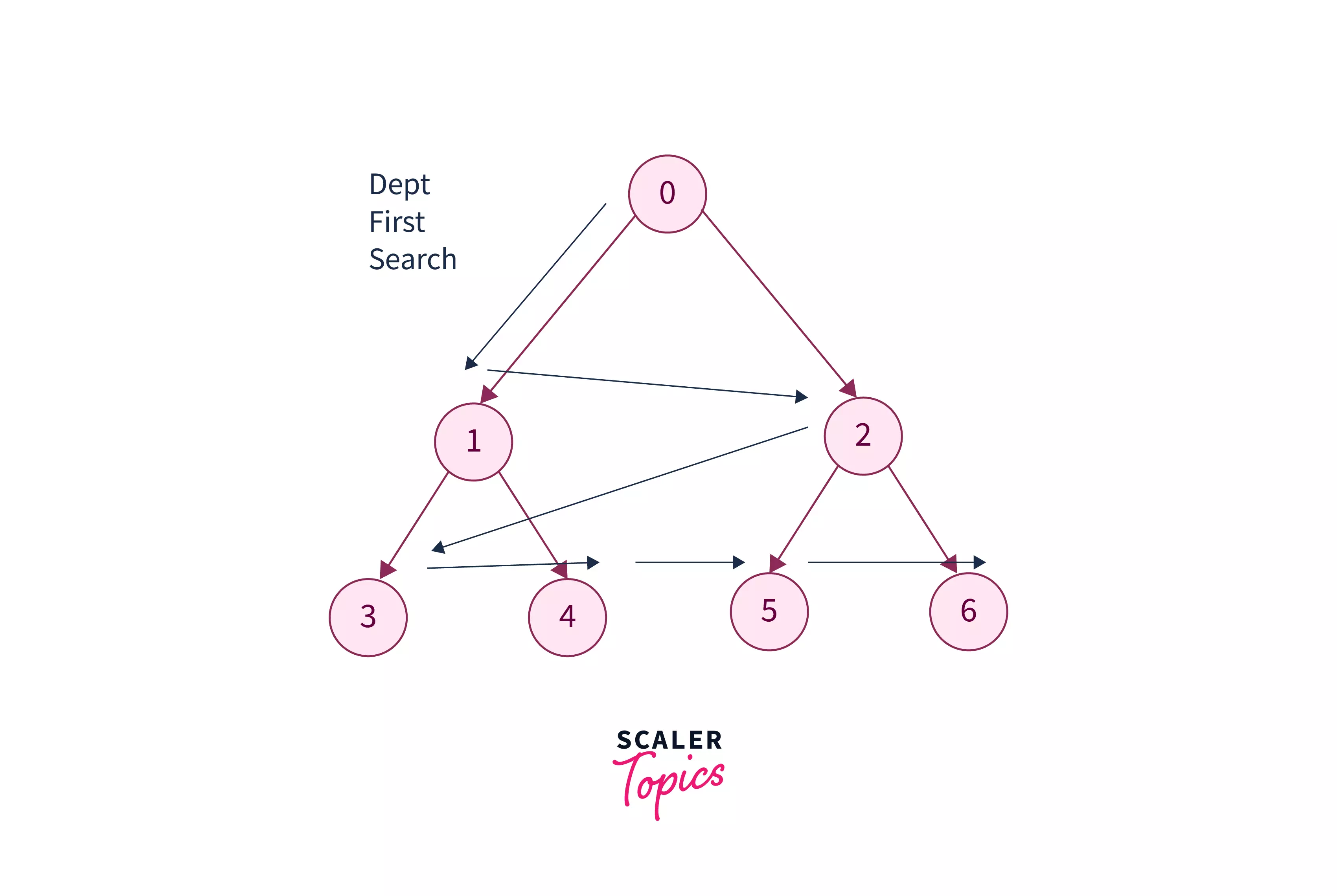
To know more about the level order binary tree traversal, you may refer to Level Order Traversal.
Now, it’s time to understand the above mentioned tree traversal concepts in a practical way. Let us understand each of them.
1. Inorder Tree Traversal
The inorder tree traversal of binary tree is also known as the LNR traversal, because in this traversal, we first visit the left node (abbreviation L), followed by the root node(abbreviation N), and finally the right node (abbreviation R) of the tree.
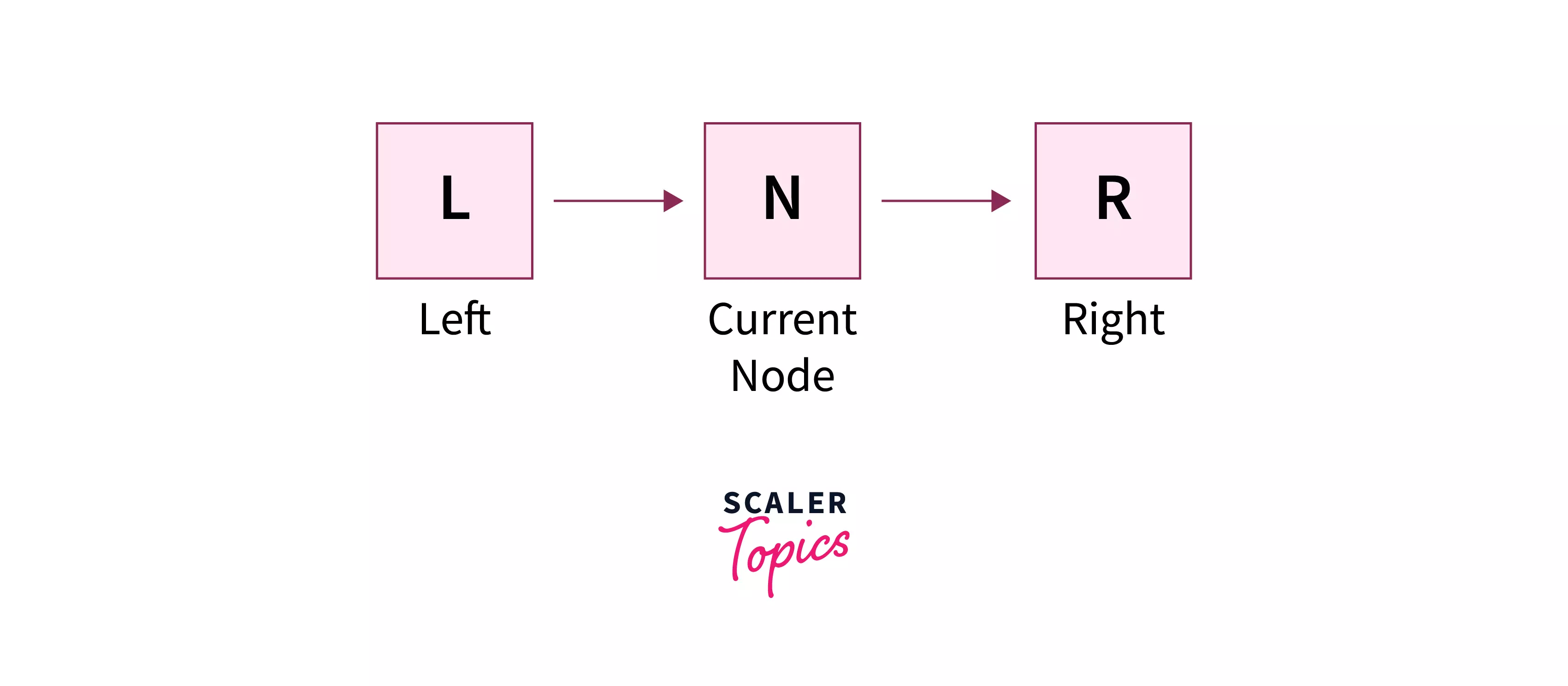
Inorder traversal of binary tree is one of the most widely used variants of the DFS (Depth First Search) traversal.
In the inorder traversal, we first start from the root node of the tree and go deeper and deeper into the left subtree in a recursive manner.
When we reach the left-most node of the tree with the above steps, then we visit that current node and go to the left-most node of its right subtree (if exists).
Following the same steps (mentioned above) recursively, helps us in traversing through the tree as a whole.
The algorithm for the inorder traversal can be stated as:
- Recursively traverse the current node’s left subtree.
- Visit the current node.
- Recursively traverse the current node’s right subtree.
Simply put:
- Go to the left subtree
- Visit the Current Node
- Go to the right subtree
Let us also write the pseudocode for the recursive inorder traversal of a binary tree:
Example:
Pseudocode for the Recursive Inorder Traversal:
#Pseudocode of recursive inorder traversal
procedure inorder(node)
if node = null
return
inorder(node.left)
visit(node)
inorder(node.right)Explanation:
In the above code, we have just traversed the complete tree by recursively calling the left subtree, and once we reach a point where there is no more left node (or it is the leaf node), we backtrack to the node’s parent node and perform our operation (print that node or perform any search activity on the node, etc). Having done that, we recursively call the inorder function to the right subtree. This process continues till we have visited all the nodes of our binary tree.
Let us take an example to clearly understand how does the inorder traversal of a binary tree works.
Below given is the image of a binary tree, where its inorder traversal is performed.
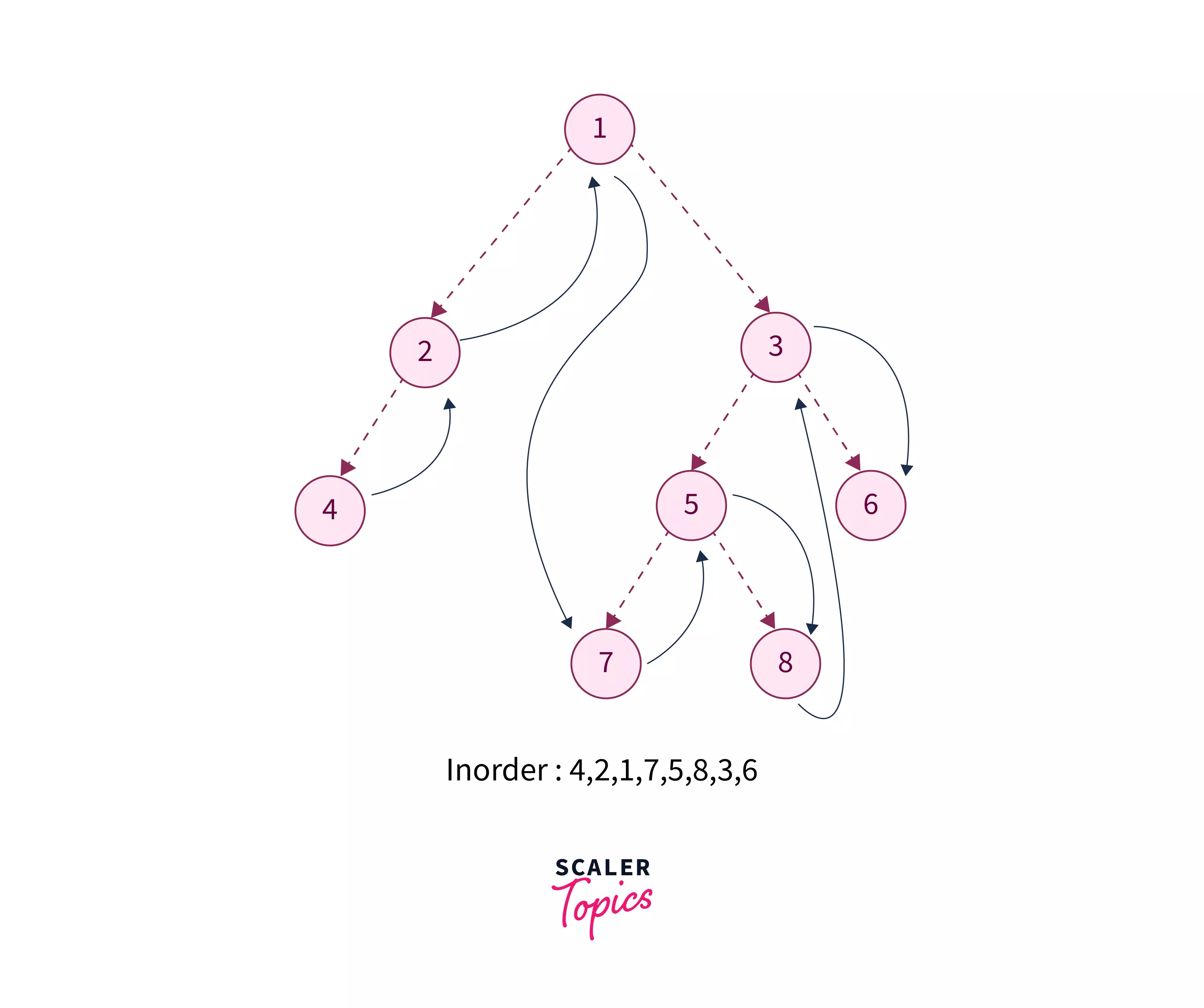
In the image, the dotted lines indicate the order in which we will visit each node. The blue lines indicate that we are going back (backtracking) after visiting a particular node.
Steps:
- At first, we traverse through the leftmost nodes, till we reach a leaf node, and do not have any node after that (or Null), since, in inorder traversal, we traverse through
left -> root -> right. - Once we reach the leaf node, we print the current node’s value(print
4here) and backtrack(marked in blue) and then print the value of that node (after that print2here, followed by 1) - We perform the same till we find the right child.
- In that case, we go deep to the right child and print its value. We recursively follow these steps till we have traversed all the nodes of the tree.
One more popular way of inorder traversal is through iteration. We can iteratively traverse all the nodes, however, it is complicated as compared to the normal recursive traversal. The pseudocode for the iterative traversal of the binary tree is given below.
Pseudocode for the Iterative Inorder Traversal:
procedure iterativeInorder(node)
stack ← empty stack
while not stack.isEmpty() or node ≠ null
if node ≠ null
stack.push(node)
node ← node.left
else
node ← stack.pop()
visit(node)
node ← node.rightSteps involved:-
- Initialize an empty stack
- Run a while loop till the stack becomes empty $OR$ the node provided to the function is $null$ .
- Inside the while loop :-
- Check if the node is not null :
- In that case, push the node inside the stack
- And go to the node’s left.
- If the node is null (or we have reached a child node):
- Pop the stack’s element (
stack.top()), and mark it as visited, or print that node - Go to the current node’s right
- Pop the stack’s element (
- Check if the node is not null :
- Continue
step 3till the stack becomes empty or the node becomes null.
Time Complexity Analysis:
In general, if we want to analyze the time complexity of a tree traversal then we have to think in the terms of the number of nodes visited.
Hence, if a tree has $n$ nodes, then each node is visited only once in inorder traversal and hence the complexity of the inorder traversal of the binary tree is $O(n)$ .
Space Complexity Analysis:
The space complexity of the recursive inorder traversal is $O(h)$ for a tree of height $h$. The height of the tree is the length of the deepest node from the root.
This might look weird that the space complexity is $O(h)$, and not equal to $O(n)$, where $n$ is the number of nodes in the tree. But, in general, space complexity of recursion is always the height/depth of recursion stack.
This is because, once we are returning (or backtracking) from our visited nodes, then their addresses are removed from the stack. And, that space is re-used when we are making a new call from a level that is closer to the root. So the maximum numbers of memory addresses on the stack at any given time are the tree height.
However, in the case of a skewed tree, the height of the tree may be equal to the number of nodes in the tree, hence leading to an overall space complexity of $O(n)$ .
Applications of Inorder Traversal:
In-order traversalis very commonly used on binary search trees because it returns the value of the tree in a sorted manner. More specifically, in an ascending (non-decreasing) order.
2. Preorder Tree Traversal
Just like the previously discussed inorder traversal, preorder traversal of binary tree is also a variant of the DFS. It is performed in a similar way as the inorder traversal is performed, but here the order of visiting the nodes is different than that of the inorder traversal.
In the case of the preorder traversal of binary tree, we visit the current node first. After that, we visit the leftmost subtree. Once we reach the leaf node(or have covered all the nodes of the left subtree), we move towards the right sub-tree. In the right subtree, we recursively call our function to do the traversal in a similar manner.
It follows the NLR structure. It means first visit the current node, followed by recursively visiting the left subtree and then the right subtree. Below given is an image for the same.
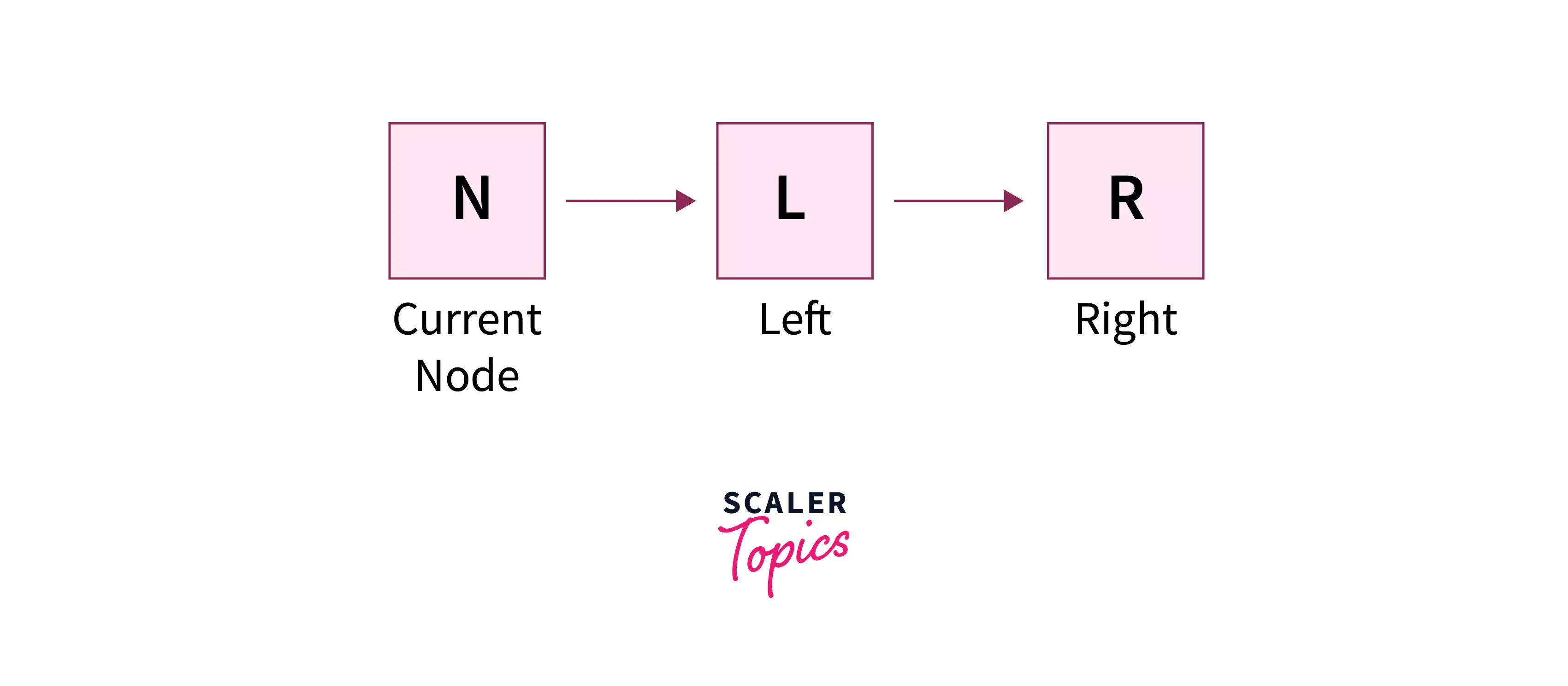
The algorithm for the preorder traversal of binary tree can be stated as:
- Visit the current node
- Recursively traverse the current node’s left subtree.
- Recursively traverse the current node’s right subtree.
FYI: The pre-order traversal is a topologically sorted one because a parent node is processed before any of its child nodes is done.
Example:
Let us see the pseudocode for the preorder traversal of binary tree.
Pseudocode for the Recursive Pre-order Traversal:
procedure preorder(node)
if node = null
return
visit(node)
preorder(node.left)
preorder(node.right) Explanation:
Let us take an example to clearly understand how the preorder traversal of the binary tree works.
Below given is the image of a binary tree, where its preorder traversal is performed.
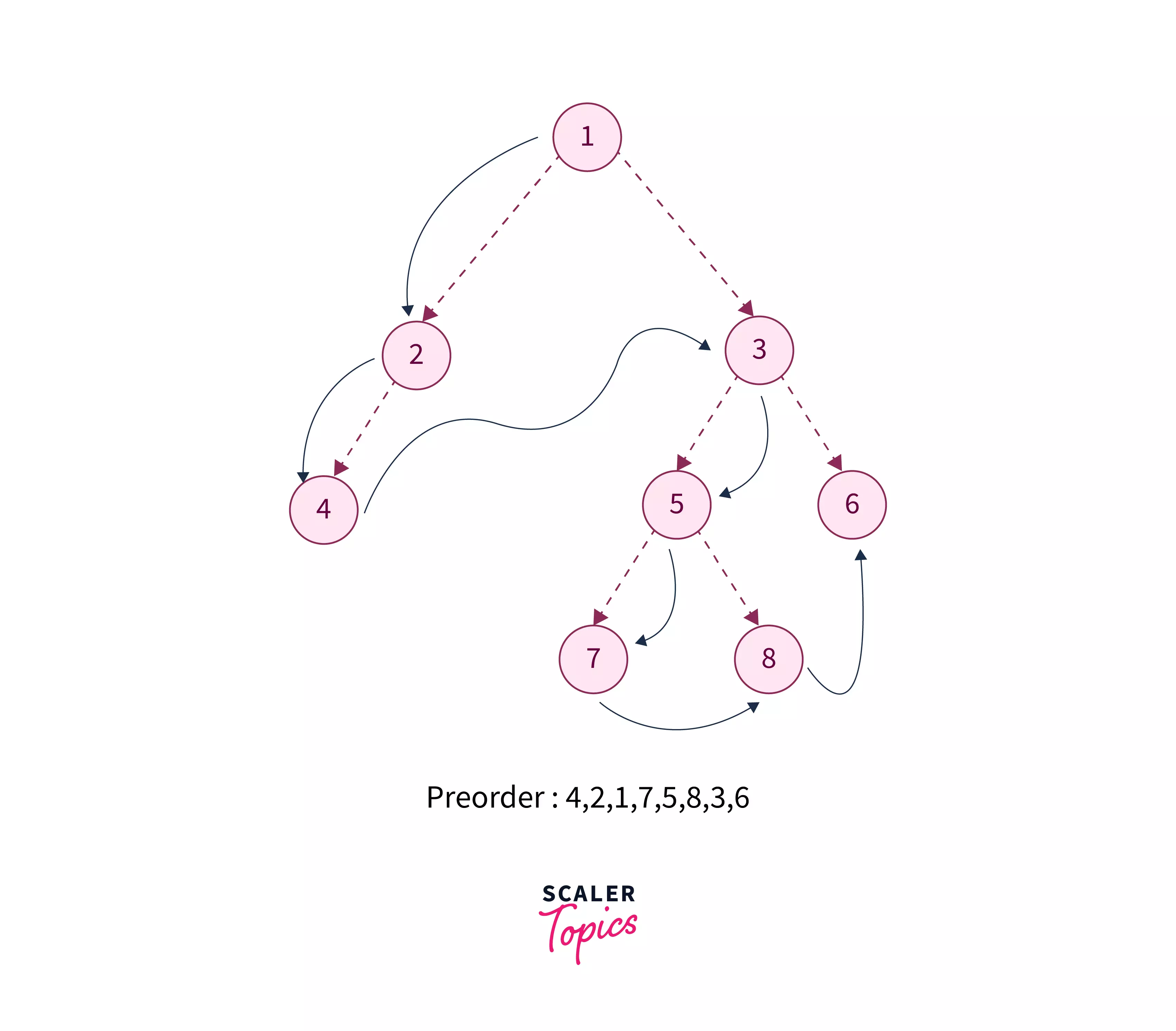
In the image, the dotted lines indicate the order in which we will visit each node. The blue lines indicate that we are going back (backtracking) after visiting a particular node.
From the above image it must be very clear that only after processing a particular node, the left subtree is processed, followed by the right subtree. These operations are defined recursively for each of the nodes. And hence, this recursive implementation is referred to as a Depth-first search (DFS), as the search tree is deepened as much as possible on each child before going to the next sibling.
For example, in the above image, we start by visiting the root, followed by the next nodes in the left subtree. After that, we recursively visit our right subtree.
Just like the inorder traversal, another popular way of preorder traversal is through iteration. We can iteratively traverse all the nodes, however, it is complicated as compared to the normal recursive traversal. The pseudocode for the iterative traversal of the binary tree is given below.
Pseudocode for the Iterative Preorder Traversal:
procedure iterativePreorder(node)
if node = null
return
stack ← empty stack
stack.push(node)
while not stack.isEmpty()
node ← stack.pop()
visit(node)
# right child is pushed first so that left is processed first
if node.right ≠ null
stack.push(node.right)
if node.left ≠ null
stack.push(node.left)
Steps Involved:
- We first make sure if the root node is not null, in that case, we simply return.
- After that, we initialize our stack as empty. We also push the current node (root node) in our stack.
- We run a while loop through the stack, where the termination condition is when the stack becomes empty.
- Inside the while loop:
i. Pop the top element of the stack, and store it in a variable ( here “node” ). Mark that node as visited (or print the value of that node)
ii. Check if the right of the node exists. In that case, push the right sub-tree of the node into the stack.
iii. Check if the left subtree of the node exists. If it exists, then push it into the stack. - Continue the steps i, ii, and iii till the stack becomes empty.
An important point to be noted here is that, although the order in which the preorder traversal of binary tree occurs is, $Current -> Left -> Right$ , we pushed the right element before the left element in the stack. The main reason for doing so is, since the stack data structure follows the LIFO property, i.e. last in first out, so we push our left subtree at last so that it gets processed before the right subtree.
Time complexity Analysis:
If a tree has $n$ nodes, then each node is visited only once in the preorder traversal of binary tree, hence the complexity of the preorder traversal of the binary tree is $O(n)$.
Space Complexity Analysis:
The space complexity of the recursive preorder traversal of binary tree is $O(h)$ for a tree of height $h$. The height of the tree is the length of the deepest node from the root. This is because space complexity of recursion is always the height / depth of recursion. We have already discussed the reason for so in our inorder tree traversal space complexity analysis. However, in the case of a skewed tree, the height of the tree may be equal to the number of nodes in the tree, hence leading to an overall space complexity of $O(n)$ .
Applications of Preorder Traversal:
Pre-order traversalof binary tree can be used to make a prefix expression (Polish notation) from the expression trees.- Preorder traversal of binary tree is also used to create a copy of the tree. For example, if we want to create a replica (copy) of a tree, we simply put the nodes of the tree in an array with a pre-order traversal. Then, for each value of the array, we perform the insert operation on a new tree. Finally, we get a copy of the original tree.
- The pre-order traversal of binary tree also outputs the topologically sorted order, because a parent node is processed before any of its child nodes is done.
3. Postorder Traversal
After having discussed a lot on inorder and preorder traversal of binary tree, you might have actually understood how they apply dfs for their traversal. Similar to them is the Postorder traversal of binary tree, where, we basically visit the left subtree and the right subtree before visiting the current node in recursion.
Postorder follows the L->R->N order of traversing the binary tree.
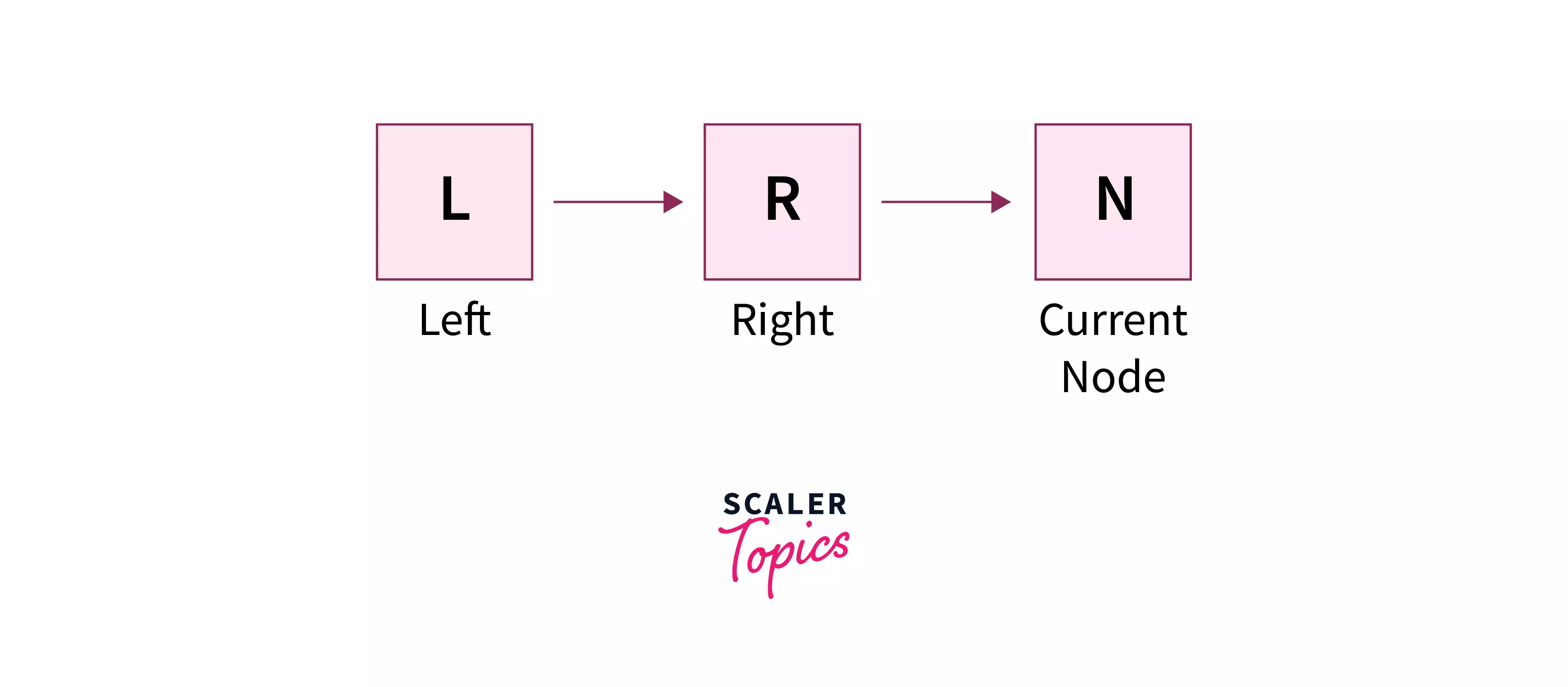
In a nutshell, postorder traversal of binary tree follows the following order of visiting the nodes in a tree:
- Recursively traverse the current node’s left subtree.
- Recursively traverse the current node’s right subtree.
- Visit the current node (in the figure: position blue).
Let us now discuss the iterative and the recursive algorithms for the postorder traversal of a binary tree.
Example:
Pseudocode for the Recursive Post-order Traversal:
procedure postorder(node)
if node = null
return
postorder(node.left)
postorder(node.right)
visit(node)
Explanation:
Following are the steps involved in the postorder traversal of binary tree:
- The base case for our recursive function is checking the current node, whether it is null or not. If it is null, we simply return from our function.
- If the current node is not null, we recursively travel to the left sub-tree using node.left (if it exists).
- Then we recursively visit the right subtree using the node.right (if it exists).
- Finally, we mark our current node as visited and perform our required operation (such as printing the node).
Let us take an example to clearly understand how does the postorder traversal of the binary tree works.
Below given is the image of a binary tree, where its postorder traversal is performed.
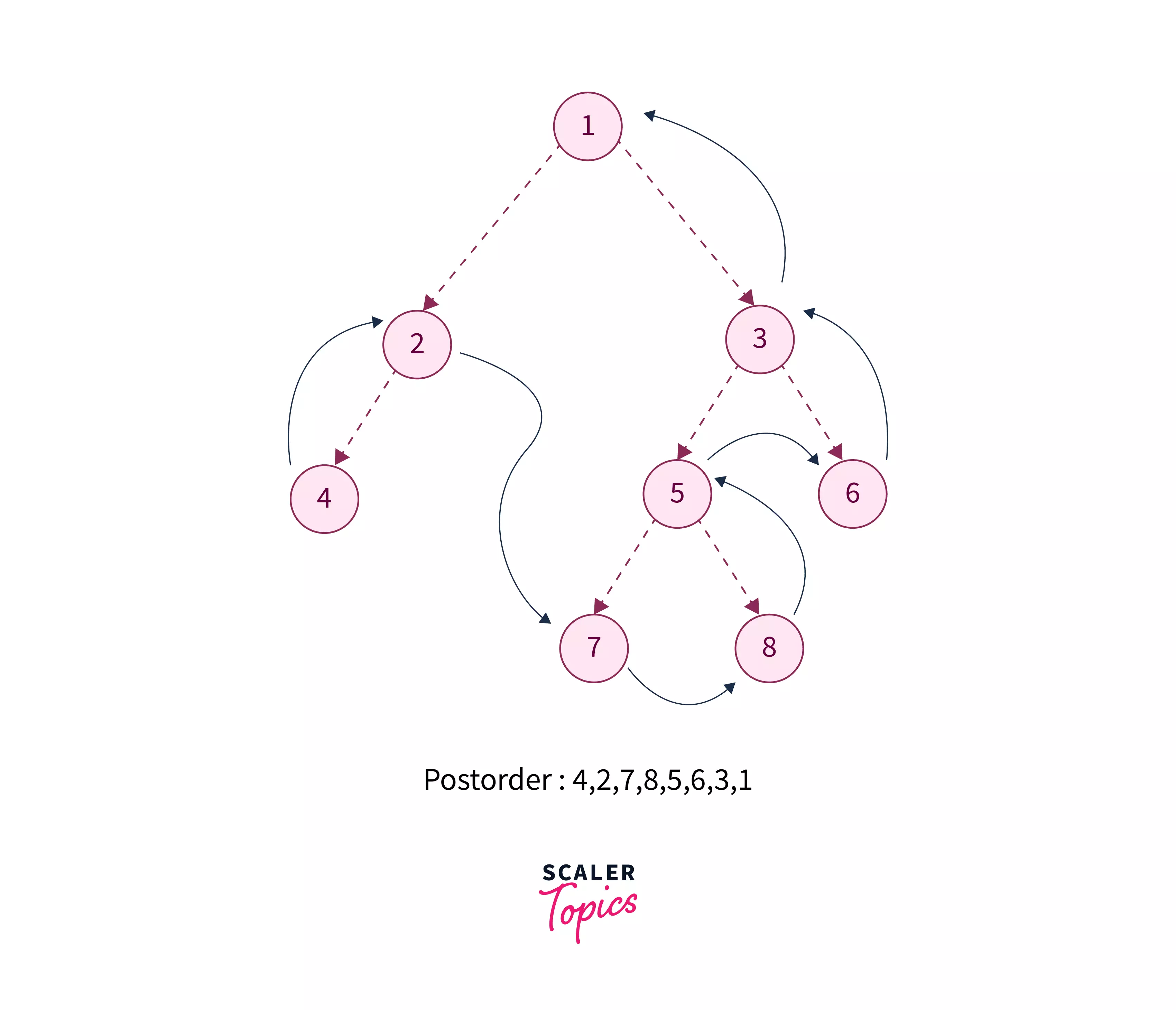
In the image, the dotted lines indicate the order in which we will visit each node. The blue lines indicate that we are going back (backtracking) after visiting a particular node.
In the above image, we can see that, before processing any node, the left subtree is processed first, followed by the right subtree, and the node is processed last. These operations can be defined recursively for each node.
Pseudocode for the Iterative Postorder Traversal:
procedure iterativePostorder(node)
stack ← empty stack
lastNodeVisited ← null
while not stack.isEmpty() or node ≠ null
if node ≠ null
stack.push(node)
node ← node.left
else
peekNode ← stack.peek()
# if right child exists and traversing node
# from left child, then move right
if peekNode.right ≠ null and lastNodeVisited ≠ peekNode.right
node ← peekNode.right
else
visit(peekNode)
lastNodeVisited ← stack.pop()
The iterative version of the postorder traversal of binary tree is so not straightforward as the inorder and preorder traversal of binary tree (but a popular question among interviewers). Let us look into the steps involved in the postorder traversal of binary tree.
Steps Involved:
- We initialize an empty stack
- We also keep a variable lastNodeVisited and initialize it to null.
- We run a while loop through our stack, with the condition that the stack should not be empty or the node should not be null.
- Inside the while loop, we check if the node is not null,
i. Then simply push it inside the stack.
ii. Point node to node.left - In case the node is null:
i. Peek through the stack’s top and store it in a variable (peekNode here)
ii. if the peekNode.right is not null and the lastNodeVisited is not equal to the peekNode.right then simply point the current node to the peekNode.right
iii. If any of the above conditions don’t meet:
iv. Mark the peekNode as visited
v. Pop from the stack’s top and store it in the lastNodeVisited. - Repeat the points 4 and 5 till the stack becomes empty.
Time Complexity Analysis:
If a tree has $n$ nodes, then each node is visited only once in the postorder traversal of binary tree, hence the complexity of the postorder traversal of the binary tree is $O(n)$ .
Space Complexity Analysis:
The space complexity of the recursive postorder traversal of binary tree is $O(h)$ for a tree of height $h$. The height of the tree is the length of the deepest node from the root. This is because space complexity of recursion is always the height/depth of recursion. We have already discussed the reason for so in our inorder tree traversal space complexity analysis. However, in the case of a skewed tree, the height of the tree may be equal to the number of nodes in the tree, hence leading to an overall space complexity of $O(n)$.
Applications of Postorder Traversal:
- Post-order traversal of binary tree can generate a postfix representation (Reverse Polish notation) of a binary tree.
- Postorder traversal of binary tree is also used to delete the tree. Because it is easier in post-order traversal where each node is freed after freeing its children.
Conclusion
In this article, we learned about the binary tree traversals in data structure, inorder traversal of the binary tree, preorder traversal of binary tree, and the postorder traversal of the binary tree.
Let’s take a brief pause and reflect on what we have seen so far!
- Traversal of binary tree refers to the process of visiting (e.g. retrieving, updating, or deleting) each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited.
- Binary Trees in data structure may be traversed in
depth-firstorbreadth-first order. - There are three common ways to traverse them in depth-first order: in-order, pre-order and post-order.
- In the inorder traversal of the binary tree, we first visit the left subtree, followed by the current node and finally the right subtree. This traversal is widely used in
BSTs. - In the
pre-ordertraversal of binary tree, we traverse from the root to the left subtree and then to the right subtree. It is used in creating prefix expressions from an expression tree, or to copy a tree - In the
post-ordertraversal of binary tree, traverse from the left subtree to the right subtree and then to the root. It is useful in deleting trees and generating postfix expressions of binary trees.
In a nutshell:
| Traversal | First | Second | Third |
|---|---|---|---|
| Inorder | Left | Root | Right |
| Preorder | Root | Left | Right |
| Postorder | Left | Right | Root |
See Also
I encourage you to go ahead and pick one of the scaler articles mentioned below to get an in-depth view of binary tree and tree data structures: