Problem Statement
The width of each and every bar on to an elevation map is 1. Determine how much water it can hold after it rains by computing the heights of the elevation map bars, which are represented by n non-negative integers.
Example
Input:
height[]=[4,3,0,2,0,2,3]
Output:
8
Example Explanation
Representation of above input heights is given below in the form of an elevation map:
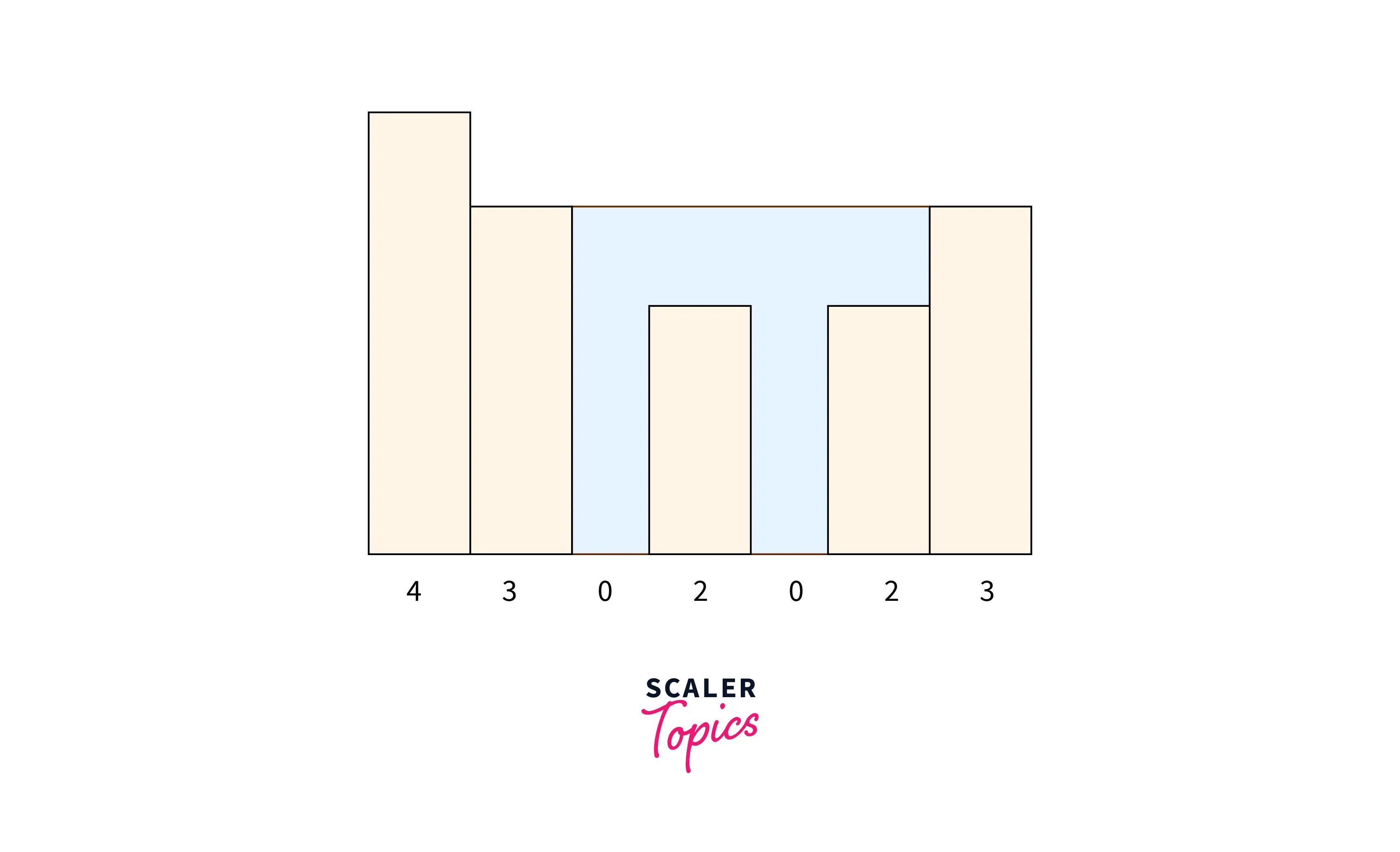
Here:
- 3 units of water can be trapped inside the first block.
- 1 unit water can be trapped inside the second block.
- 3 units of water can be trapped inside the third block.
- 1 unit water can be trapped inside the fourth block.
Hence, Trapped Water= 3×1 + 1×1 + 3×1 + 1×1 = 8(Area of water in the container.)
An idea behind solving trapping rain water problem is that the rain water can only be stored in some block when there is an existence of greater height block(in both left and right side of the current block) then the current block. By this rain water get trapped onto the top of the current block.
So it is clear that the amount of water that can be trapped is equal to the minimum of maximum heights that are present in both left and right side of the current block minus height of current block.
Then, Amount_of_water[i] = min(right_max_height, left_max_height) – blocks[i]
Constraints
Constraints for trapping rain water are given below.
n = height.length
1 <= n <= 2 * 10^4
0 <= height[i] <= 10^5
Approach 1 (Bruteforce Approach)
First approach for trapping rain water that is the bruteforce one is given below. Simply go through each element of the array Arr[], as our task is to determine the maximum height on the left and right side for each element(i.e block) of the array. Find the highest highest point on the left and the highest point on the right for each element(i.e block). Add min(right_max_height, left_max_height)-Arr[i] as a result(trapped water) in current block.
Algorithm
Steps for this approach are given as below:
- Create res variable and initialise it’s value as 0.
- For each value traverse an array Arr[] from 1-n:
- Set left_maximum and right_maximum to 0 at initialization.
- Update left max by moving Arr[i] to the beginning of array:
- left_maximum = max(left_maximum, Arr[i])
- In similar way update right max by moving A[i] till the end of an array.
- right_maximum = max(right_maximum, Arr[i])
- Add min(left_maximum, right_maximum) – Arr[i] to res.
Code Implementation
Code implementation of trapping rain water is given below in all three languages(c++, java, python).
Implementation of the Bruteforce Method Using C++
class Solution {
public:
int trap_rainwater(vector<int>& Arr) {
int ans = 0;
for (int k = 1; k < Arr.size() - 1; k++) {
//Finding left_maximum
int left_maximum = INT_MIN;
for (int l = k - 1; l >= 0; l--) {
left_maximum = max(left_maximum, Arr[l]);
}
//Finding right_maximum
int right_maximum = INT_MIN;
for (int m = k + 1; m < Arr.size(); m++) {
right_maximum = max(right_maximum, Arr[m]);
}
//Finding volume of water can stored
int maximum_water = min(left_maximum,right_maximum);
ans += maximum_water - Arr[k];
}
return ans;
}
};
Implementation of the Bruteforce Method Using Java
public static int trap_rainwater(int[] Arr, int N){
int ans = 0;
for(int k = 0; k < N ; k++){
int left_maximum= arr[k];
for(int l = k - 1; l >= 0; l--){
left_maximum = Math.max(left_maximum, Arr[l]);
}
int right_maximum = Arr[k];
for(int l = k + 1; l < n; l++){
right_maximum = Math.max(right_maximum, Arr[l]);
}
ans += Math.min(left_maximum, right_maximum) - Arr[k];
}
return ans;
}
Implementation of the Bruteforce Method Using Python
def trap_rainwater(Arr, N) :
ans = 0;
for k in range(1, N-1) :
left_maximum = Arr[k];
for l in range(k) :
left_maximum = max(left_maximum, Arr[l]);
right_maximum = Arr[k];
for l in range(k + 1 , n) :
right_maximum = max(right_maximum, Arr[l]);
ans = ans + (min(left_maximum, right_maximum) - Arr[k]);
return ans;
Output
8
Time Complexity
O(n^2) as for each individual value right and left side is traversed.
Space Complexity
O(1) as no additional space is used while implementing this approach.
Approach 2 (Prefix and Suffix Arrays)
Second approach for trapping rain water that is using prefix and suffix arrays is given below. Now we will increase the efficiency from O(N^2) to O(N). Keep in mind that we are traversing left as well as right for each element when using brute force. If we store this data, we can solve the issue with just one traversal, effectively lowering the time complexity to O(N).
It is suggested to think of two arrays, left max and right max where left max[i] will store the highest point on the left up to index i. Similar to that, right max[i] will keep track of the right’s maximum height up until index i.
Algorithm
- Create two arrays i.e right max and left max of size n.
- Create a variable m = 0.
- Keep traversing from left to right and updating mxi = max(mxi, Arr[i]), and setting left maximum = mxi for an each index i.
- In a similar manner, traverse a loop from N to 1 and update mxi = max(mxi, Arr[i]) and allocate right maximum = mxi for an each index i.
- Set a variable ans initial value to 0, then go from 0 to N-1. Add min(left maximum[i], right maximum[i]) – Arr[i] to ans for an each index i.
Code Implementation
Code implementation of trapping rain water is given below in all three languages(c++, java, python).
Implementation in C++
class Solution {
public:
int trap_rainwater(vector<int>& Arr){
int ans = 0;
int N = Arr.size();
int left_maximum[N], right_maximum[N];
int mxi = INT_MIN;
for (int k = 0; k < N; k++) {
mxi = max(mxi, Arr[k]);
left_maximum[k] = mxi;
}
mxi = INT_MIN
for (int k = N - 1; k >= 0; k--) {
mxi = max(mxi, height[k]);
right_maximum[k] = mxi
}
for (int k = 0; k < N ; k++) {
ans += min(left_maximum[k], right_maximum[k]) - Arr[k];
}
return ans;
}
};
Implementation in Java
public int trap_rainwater(int[] Arr) {
if (Arr.length == 0)
return 0;
int[] leftMaximum = new int[Arr.length];
int[] rightMaximum = new int[Arr.length];
leftMaximum[0] = Arr[0];
for (int k = 1; k < leftMaximum.length; k++) {
leftMaximum[k] = Math.max(leftMaximum[k - 1], Arr[k]);
}
rightMaximum[Arr.length - 1] = Arr[Arr.length - 1];
for (int k = rightMaximum.length - 2; k >= 0; k--) {
rightMaximum[k] = Math.max(rightMaximum[k + 1], Arr[k]);
}
int ans = 0;
for (int k = 0; k < Arr.length; k++) {
ans += Math.min(leftMaximum[k], rightMaximum[k]) - Arr[k];
}
return ans;
}
Implementation in Python
def trap_rainwater(self, Arr: List[int]) -> int:
N = len(Arr)
left_maximum = N * [0]
right_maximum = N * [0]
ans = 0
for k in range(N):
if k == 0:
left_maximum[k] = Arr[k]
right_maximum[N-1-i] = Arr[n-1-k]
else:
left_maximum[k] = max(left_maximum[k-1], Arr[k])
right_maximum[n-1-k] = max(right_maximum[n-k], Arr[N-1-k])
for k in range(N):
ans += (min(left_maximum[k], right_maximum[k]) - Arr[k])
return ans
Time Complexity
O(N) + O(N) = O(N), as the array is traversed thrice. Once we have traversed the array for evaluating the left_maximum and right_maximum of each block, then on second traversal we are calculating the amount of water can be filled in each block according to left_maximum and right_maximum of that block.
Space Complexity
O(N), as we are creating 2 arrays of combined size n, it means we are using ‘n’ extra space.
Approach 3 (Using Stacks)
The arrays are been traversed two times in DP approach. Can the strategy for a single scan be improved? An idea here is to monitor an area between current block Arr[i] and all of the preceding blocks in an array that have smaller heights. To keep track of the index of the earlier smaller blocks, we can just use a stack.
Algorithm
- Make a stack name S.
- Traversed an array from the left to right:
- If current block Arr[i] is larger than the value that is there on the top of stack, then it means that block which is there in the top of stack is confined between current and previous block in stack. Then we will pop that value from top of the stack and add amount of water that is stored between blocks to the total trapped water.
- This formula can be used to determine the total amount of water:
- Length= curr index i – St.top() – 1
- Width = min(Arr[i],Arr[St.top()]) – Arr[top]
- Add Length∗Width i.e the total volume into res.
Implementation of the Stack Method Using C++
Code implementation of trapping rain water is given below in all three languages(c++, java, python).
class Solution {
public:
int trap_rainwater(vector<int>&Arr){
int ans = 0;
int N = Arr.size();
stack<int>St;
int k = 0;
while(k < N){
while(!St.empty() and Arr[k] > Arr[St.top()]){
int top_ele = Arr[St.top()];
St.pop();
if(St.empty()) break;
int len = k - St.top() - 1;
int wid = min(Arr[k], Arr[St.top()]) - Arr[top_ele];
ans += len * wid;
}
St.push(k);
k = k + 1;
}
return ans;
}
};
Implementation of the Stack Method Using Java
public int trap_rainwater(int[] Arr) {
int N = Arr.length;
int ans = 0;
Stack<Integer> st = new Stack<Integer>();
int k = 0;
while(k < N){
while (!st.isEmpty() && Arr[k] > Arr[st.peek()]){
int top = Arr[st.peek()];
st.pop();
if(st.isEmpty()){
break;
}
int len = k - st.peek() - 1;
int wid = Math.min(Arr[k], Arr[st.peek()]) - Arr[top];
ans += len * wid;
if (Arr[top]<=Arr[i]) {
st.pop();
}
}
st.push(i);
k = k + 1;
}
return ans;
}
Implementation of the Stack Method Using Python
def trap_rainwater(Arr):
st = []
ans = 0
for k in range(len(Arr)):
while st and Arr[k] > Arr[st[-1]]:
pop_ele = st.pop()
if st:
left_side = Arr[st[-1]]
right_side = Arr[i]
ans += (min(right_side, left_side) - Arr[pop])*(k-st[-1]-1)
st.append(k)
return ans
Output
8
Time Complexity
O(N), as array is been traversed only once for n number of values
Space Complexity
O(N), as we have used extra N sized stack for storing values.
Approach 4 (Horizontal Scan Method)
The tallest block’s height will determine the maximum height to which any rainwater that has been trapped may rise. And we can count number of blocks that will store water by moving bottom to max height for each paricular block while traversing blocks from left to right.
Algorithm
- Find total number of blocks that is nothing but sum of array.
- Find max height in the array.
- Create a variable, total_water=0
- Create left=0 and right=0.
- For every block k from 0 to max_height, perform the following:
- While scanning height array from left side to right side if a height is greater than the current row index i ,then that will be boundary of one of the section of trapped water. Let’s store these indexes.
- Let’s take boundary indexes be boundary=[k1,k2…]
- The water kept in the current row with both k1 and k2 is equal to k2 – k1 – 1 and between k2 and k3 is equal to k3 – k2 – 1, and so forth.
- Total water that can be stored in current row = (k2 – k1 – 1) + (k3 – k2 – 1) + … (knth – k(n-1)th -1) = knth – k1 – (b–1), where b is the number of blocks.
- We won’t need to scan out the entire array if we can locate the first and last boundary indexes of each row that is k1 and kn. Since b is the number of blocks in the current row, we won’t find it. Instead, b will accumulate and add to the total no. of blocks that we have already found, and 1 will accumulate for each row, becoming max height.
- Find out k1 by moving from left towards right till you find out h where h is greater then k that is current row, similarly find out the kn by moving from right towards the left.
- Set the left = k1 and the right = kn and than add kn – k1 to the total
- The total amount of trapped water is calculated by subtracting the number of blocks from the maximum height from the total.
Implementation
Code implementation of trapping rain water is given below in all three languages(c++, java, python).
Implementation of Horizontal Scan Method Using C++
#include <bits/stdc++.h>
using namespace std;
int trap_rainwater(vector<int>&arr){
int numof_blocks = 0;
int n = 0;
int maximum_height = INT_MIN;
for(auto height : arr){
numof_blocks += height;
n += 1;
maximum_height = max(maximum_height, height);
}
int total_water = 0;
int leftside = 0;
int rightside = n - 1;
for(int k = 0; k < maximum_height; k++){
while(arr[leftside] <= k)
leftside += 1;
while(arr[rightside] <= k)
rightside -= 1;
total_water += rightside - leftside;
}
total_water -= (numof_blocks - maximum_height);
return total_water;
}
Implementation of Horizontal Scan Method Using Java
import java.io.*;
class trap {
public static int trap_rainwater(int array[]){
int n = array.length;
int numof_blocks=0;
int maximum_height = Integer.MIN_VALUE;
for(int k=0;k<n;k++){
maximum_height=Math.max(maximum_height,arrray[i]);
numof_blocks+=array[k];
}
int total_water=0,leftside=0,rightside=n-1;
for(int k=0;k<max_height;k++){
while(array[leftside]<=k){
leftside++;
}
while(array[rightside]<=k){
rightside--;
}
total_water+=rightside-leftside;
}
total_water-=numof_blocks-maximum_height;
return total_water;
}
}
}
Implementation of Horizontal Scan Method Using Python
def trap_rainwater(array):
numof_blocks = 0
n = 0
maximum_height = float('-inf')
for height_of_block in array:
numof_blocks += height_of_block
n += 1
maximum_height = max(maximum_height, height_of_block)
total_water = 0
leftside = 0
rightside = n - 1
for k in range(maximum_height):
while array[leftside] <= k:
leftside += 1
while array[rightside] <= k:
rightside -= 1
total_water += rightside - leftside
total_water -= (numof_blocks - maximum_height)
return total_water
Output
8
Time Complexity
O(maximum_height*h), here h is the total value of change between the leftside pointer and rightside pointer.
Space Complexity
O(1), as no additional space has been used.
Approach 5 (Using Two Pointers)
Create two pointers: one on the array’s left side and one on its right. If there is a block on left side, the total amount of water trapped would depend in both the right-to-left and left-to-right directions.
Algorithm
- Create and set left_pointer=0, right_pointer = n-1 and ans=0.
- Create 2 variable left_maximum and right_maximum and set them as 0.
- While left_pointer<=right_pointer, keep traversing the array and:
- If Arr[left_pointer] < Arr[right_pointer]] and left_maximum > Arr[left_maximum]
- add left_maximum – Arr[left_pointer] to ans
- Else if left_maximum < Arr[left_pointer]
- Update the left_maximum to Arr[left_pointer]
- Increment the left_pointer by one
- In similar way, if Arr[left_pointer] > Arr[right_pointer] and right_maximum > Arr[right_pointer]
- add right_maximum – Arr[right_maximum] to ans
- Else if right_maximum < Arr[right_maximum]
- Update the right_maximum to Arr[right_pointer]
- Increment the right_pointer by one.
- If Arr[left_pointer] < Arr[right_pointer]] and left_maximum > Arr[left_maximum]
- Print the ans.
Implementation
Code implementation of trapping rain water is given below in all three languages(c++, java, python).
Implementation of Horizontal Scan Method Using C++
class Solution {
public:
int trap_rainwater(vector<int>&Arr)
{
int ans = 0;
int N = Arr.size();
int left_pointer = 0, right_pointer = N - 1;
int left_maximum = 0, right_maximum = 0;
while(left_pointer <= right_pointer){
if(Arr[left_pointer] < Arr[right_pointer]){
if(A[left_pointer] > left_maximum){
left_maximum = Arr[left_pointer];
}
else{
ans += left_maximum - A[left_pointer];
}
left_pointer = left_pointer + 1;
}
else{
if(Arr[right_pointer] > right_maximum){
right_maximum = A[right_pointer];
}
else{
ans += right_maximum - Arr[right_pointer];
}
right_pointer = right_pointer + 1;
}
}
return ans;
}
};
Implementation of Horizontal Scan Method Using Java
public int trap_rainwater(int[] Arr) {
int ans =0;
int left_maximum = 0;
int right_maximum = 0;
int k = 0;
int l = Arr.length -1;
while(k<l){
left_maximum = Math.max(left_maximum, Arr[k]);
right_maximum = Math.max(right_maximum, Arr[l]);
if(left_maximum < right_maximum){
ans += left_maximum-Arr[k];
k++;
}
else{
ans += right_maximum - Arr[l];
l--;
}
}
return ans;
}
Implementation of Horizontal Scan Method Using Python
def trap_rainwater(Arr):
k, l = 0, len(A) - 1
leftMax, rightMax = Arr[k], Arr[l]
ans = 0
while k < l:
left_maximum = max(left_maximum, Arr[k])
right_maximum = max(right_maximum, Arr[l])
if left_maximum < right_maximum:
ans += left_maximum - Arr[k]
k += 1
else:
ans += right_maximum - Arr[l]
l -= 1
return ans
Output
8
Time Complexity
O(n), as the array is traversed only once that is from 0 to length of array. In this traversal we are evaluating the left_maximum and right_maximum of each block.
Space Complexity
O(1), as we are creating and using any extra space over here, only 5 new variables are used here.
Conclusion
- There are five approach to solve trapping rain water problem, those are mentioned below:
- Bruteforce Approach
- Prefix and suffix arrays
- Using stacks
- Horizontal scan method
- Using two pointers
- The two pointer approach works best because it has an O(N) time complexity and an O(1) space complexity.
- The tallest block’s height will determine the maximum height to which any rainwater that has been trapped may rise.
- The total amount of trapped water is calculated by subtracting the number of blocks from the maximum height from the total.
