The Tower of Hanoi problem consists of three rods (for example A, B, and C) and N disks initially stacked on rod A in decreasing order of diameter (smallest one is at the top). The goal is to transfer the entire stack to another rod (in this case, rod C) with the help of auxiliary rod(in this case, rod B).
Example:
For an input of 2 disks:
Disk 1 moved from rod A to rod B
Disk 2 moved from rod A to rod C
Disk 1 moved from rod B to rod C
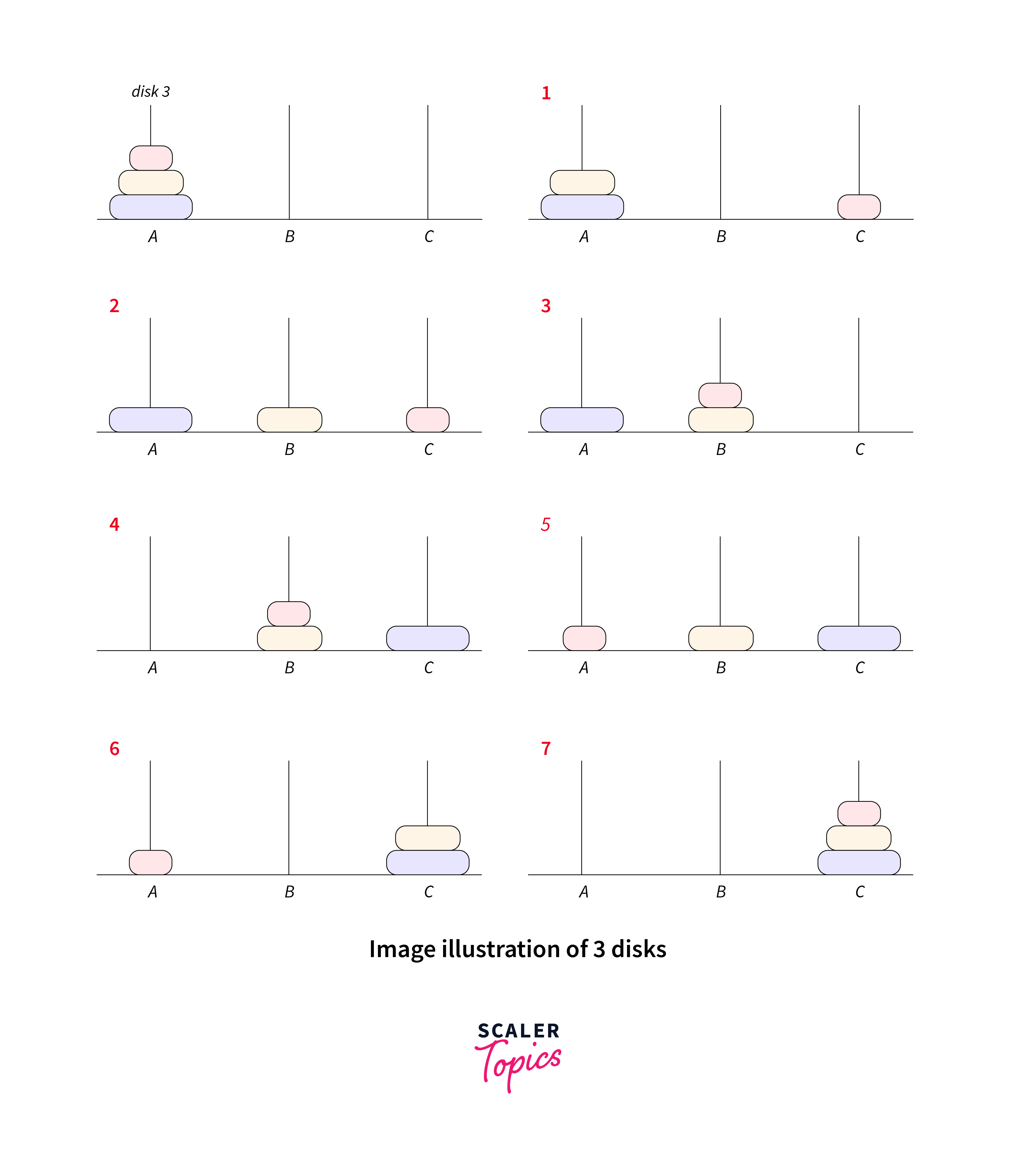
For 3 disks:
Disk 1 moved from rod A to rod C
Disk 2 moved from rod A to rod B
Disk 1 moved from rod C to rod B
Disk 3 moved from rod A to rod C
Disk 1 moved from rod B to rod A
Disk 2 moved from rod B to rod C
Disk 1 moved from rod A to rod C
Rules to be Followed During Shifting From the Source to Destination Peg
There are following three rules to be followed while solving tower of hanoi algorithm:
- We can move only one disk at a time.
- A disk can only be moved if it’s the topmost one on a stack.
- No disk should be placed at the top of the smaller disk which means that the disk of larger diameter cannot be placed on a disk of smaller diameter.
Tower of Hanoi using Recursion Algorithm
Utilize recursion to transfer disks from the source rod to the destination rod via a helper rod.
- Move ‘N-1’ disks from the source rod(A) to the auxiliary rod(B), using the destination rod (C) as the helper.
- Move the last disk from the source rod(A) to the destination(C) rod directly.
- Move the ‘N-1’ disks from the auxiliary rod(B) to the destination rod(C), using the source rod(A) as the helper.
Explanation:
Following are the steps to solve the problem:
- The function towerOfHanoi takes four parameters: N (the current number of disks to move), from_rod (the rod from which to move the disks), to_rod (the rod to which to move the disks), and aux_rod (the auxiliary rod that can be used as a temporary storage).
- If there is only one disk (base case, N == 1), move it directly from from_rod to to_rod and return.
- For N > 1, follow these steps:
- Recursively call towerOfHanoi for N – 1 disks to move them from from_rod to aux_rod, using to_rod as the auxiliary rod.
- Move the Nth disk (the bottom disk) from from_rod to to_rod.
- Recursively call towerOfHanoi for N – 1 disks to move them from aux_rod to to_rod, using from_rod as the auxiliary rod.
- The initial function call to solve the puzzle with n disks from rod A to rod C with B as an auxiliary rod would be towerOfHanoi(n, ‘A’, ‘C’, ‘B’).
Code Implementation
C++ Implementation of the Tower of Hanoi Using Recursion
// C++ program for the Tower of Hanoi using recursion
#include <bits/stdc++.h>
using namespace std;
void TowerOfHanoi(int N, char source_rod, char dest_rod, char aux_rod){
// Base case if n==0 return
if (N == 0){
return;
}
// calling the recursive function by following the pattern observed
TowerOfHanoi(N - 1, source_rod, aux_rod, dest_rod);
// printing the move which happened just
cout << "Move disk " << N << " from rod " << source_rod << " -> " << dest_rod << endl;
// calling the recursive function by following the pattern observed
TowerOfHanoi(N - 1, aux_rod, dest_rod, source_rod);
}
// Driver code
int main(){
// Number of disks in the given tower of hanoi
int N = 3;
// calling the recursive function where A-> source rod, B-> auxiliary rod, C-> destination rod
TowerOfHanoi(N, 'A', 'C', 'B');
return 0;
}
Python Implementation of the Tower of Hanoi Using Recursion
# Python program for the Tower of Hanoi using recursion
def TowerOfHanoi(N , source_rod, dest_rod, aux_rod):
# Base Case: if n==0 return
if N == 0:
return
# calling the recursive function by following the pattern observed
TowerOfHanoi(N-1, source_rod, aux_rod, dest_rod)
# printing the move which happened just
print("Move disk", N,"from rod",source_rod,"to rod" , dest_rod)
# calling the recursive function by following the pattern observed
TowerOfHanoi(N-1, aux_rod, dest_rod, source_rod)
# Driver code
# Number of disks in the given tower of hanoi
N = 3
# calling the recursive function where A-> source rod, B-> auxiliary rod, C-> destination rod
TowerOfHanoi(N, 'A', 'C', 'B')
Java Implementation of the Tower of Hanoi Using Recursion
// JAVA program for the Tower of Hanoi using recursion
import java.util.*;
import java.io.*;
import java.math.*;
class Solution{
static void TowerOfHanoi(int N, char source_rod, char dest_rod, char aux_rod){
// Base case if n==0 return
if (N == 0){
return;
}
// calling the recursive function by following the pattern observed
TowerOfHanoi(N - 1, source_rod, aux_rod, dest_rod);
// printing the move which happened just
System.out.println("Move disk "+ N + " from rod " + source_rod +" -> " + dest_rod );
// calling the recursive function by following the pattern observed
TowerOfHanoi(N - 1, aux_rod, dest_rod, source_rod);
}
// Driver code
public static void main(String args[]){
// Number of disks in the given tower of hanoi
int N = 3;
// calling the recursive function where A-> source rod, B-> auxiliary rod, C-> destination rod
TowerOfHanoi(N, 'A', 'C', 'B');
}
}
Output:
Move disk 1 from rod A -> C
Move disk 2 from rod A -> B
Move disk 1 from rod C -> B
Move disk 3 from rod A -> C
Move disk 1 from rod B -> A
Move disk 2 from rod B -> C
Move disk 1 from rod A -> C
Complexity Analysis
Time Complexity: O(2^N) i.e, For each disk, there are two possibilities. Therefore, if we have N disks, the total number of possibilities is 2 raised to the power of N. Hence, the time complexity of tower of hanoi in data structure is 2^N.
Space complexity: O(N). Auxiliary stack space used during recursion for the Tower of Hanoi algorithm.
Conclusion
- Tower of Hanoi in data structure is a classic recursion problem where disks are moved from one rod to another following specific rules.
- It can be efficiently solved using recursion by moving disks step by step.
- Demonstrated in C++, Python, and Java, showcasing versatility in solving the problem.
- Time complexity is O(2^N), space complexity is O(N), showcasing efficiency.