The top view of a binary tree consists of the set of nodes that are visible when the tree is viewed from the top. We are given a binary tree and we have to print the top view of it. The output nodes must be printed starting from the left-most horizontal level to the rightmost horizontal level of the binary tree.
Introduction
We will first look at exactly the Binary Tree before we jump over the problem statement.
Binary Tree
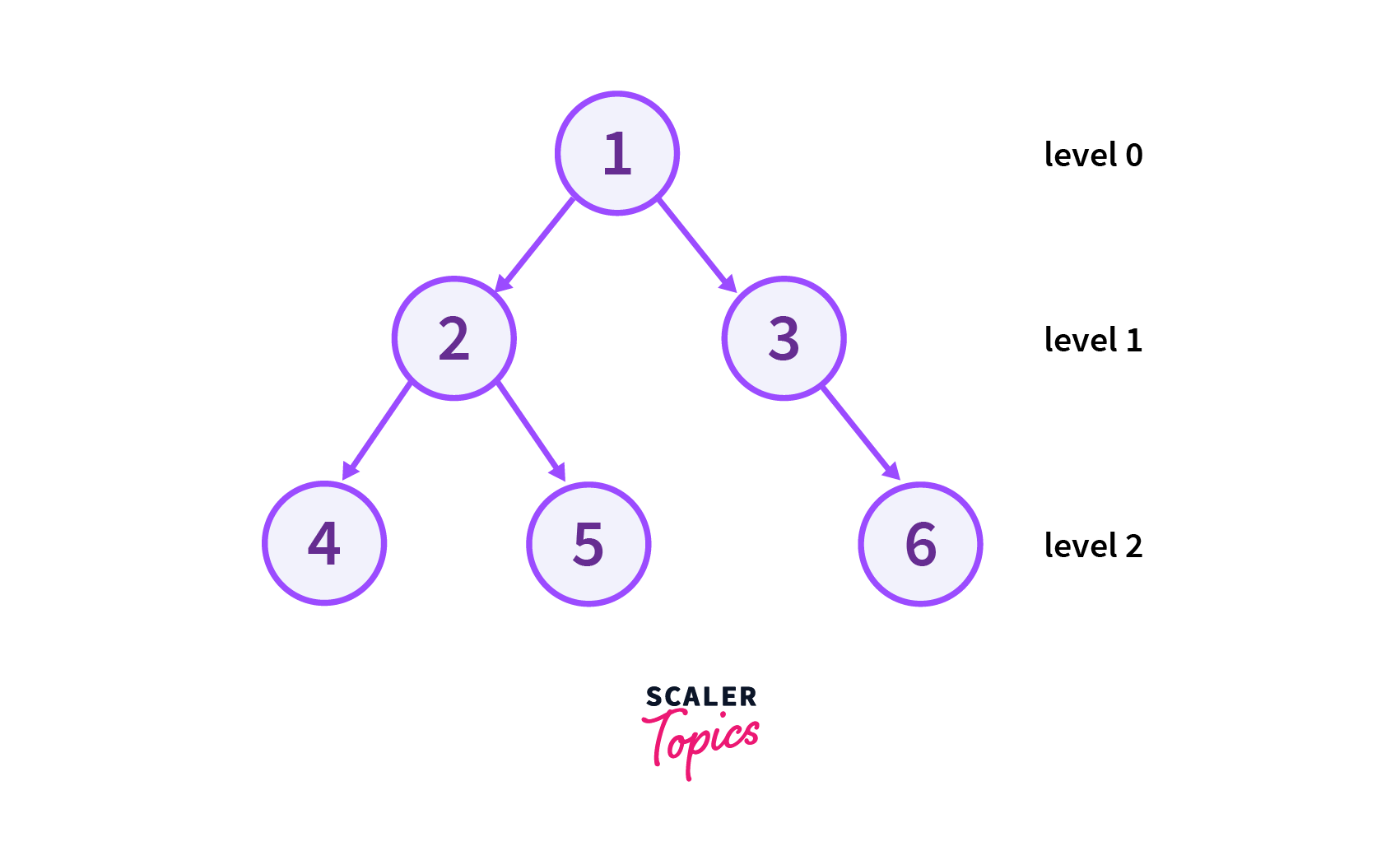
A binary Tree is a structure in which nodes are connected with each other in such a way that every node can have a maximum of two children. Since each node in a binary tree can have only two children, we typically name them the left and right children.
The following picture shows the Binary Tree in which Node 1 and 2 has two children, Node 3 has only one child and Node 4,5 and 6 (leaf nodes) have no child.
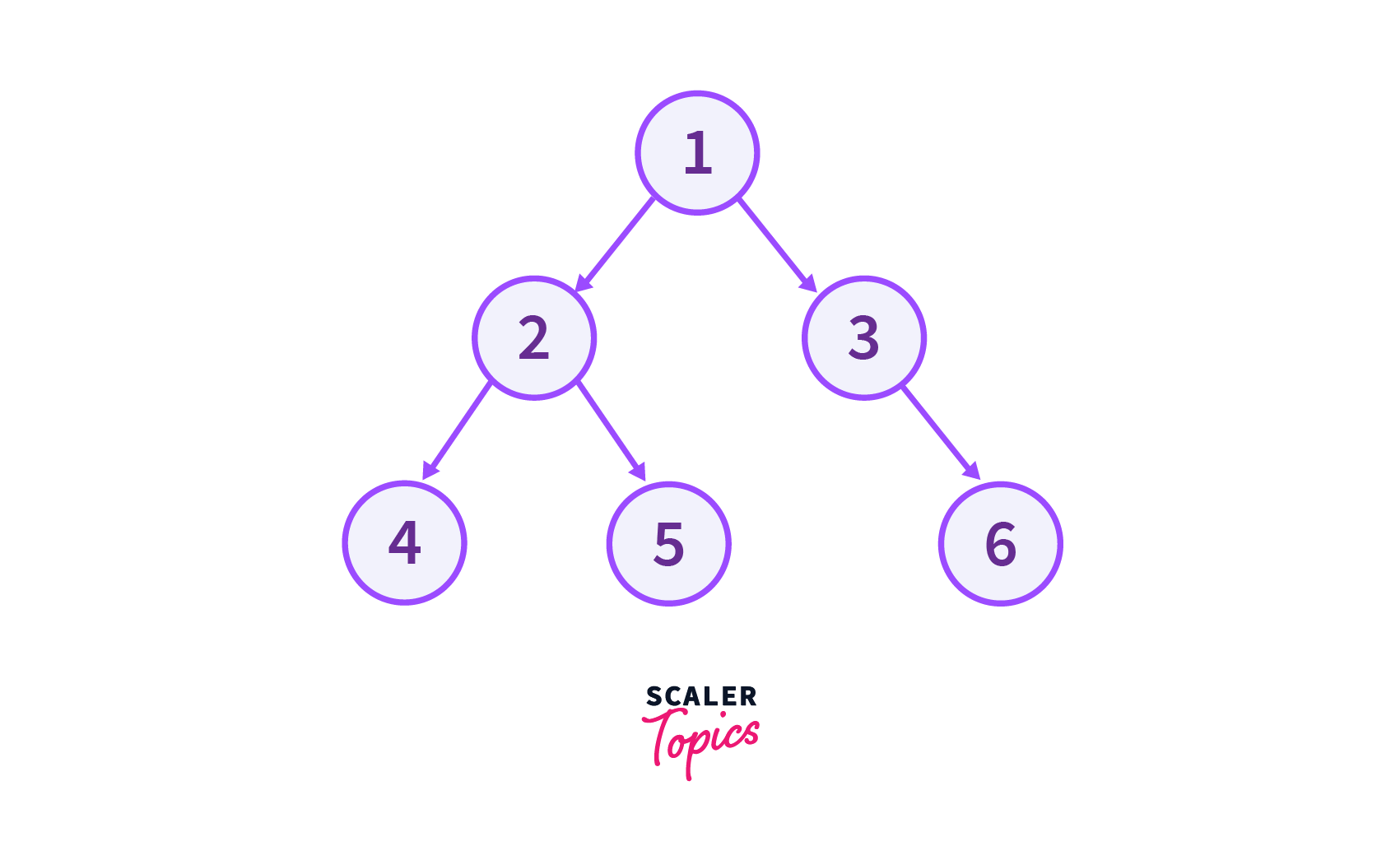
Top View of Binary Tree
In this article, we are going to look over the set of nodes that are visible when a Binary Tree is viewed from the top. We don’t have to bother about the order in which the nodes of the binary tree are to be printed while viewing them from the top view of the binary tree.
Problem Statement
Given a binary tree, print the nodes that are visible from the top view of the binary tree. Nodes should be printed in order starting from the left-most horizontal level to the rightmost horizontal level.
Example
Let us understand the above Problem Statement with the help of the following examples.
Example 1

Example 2
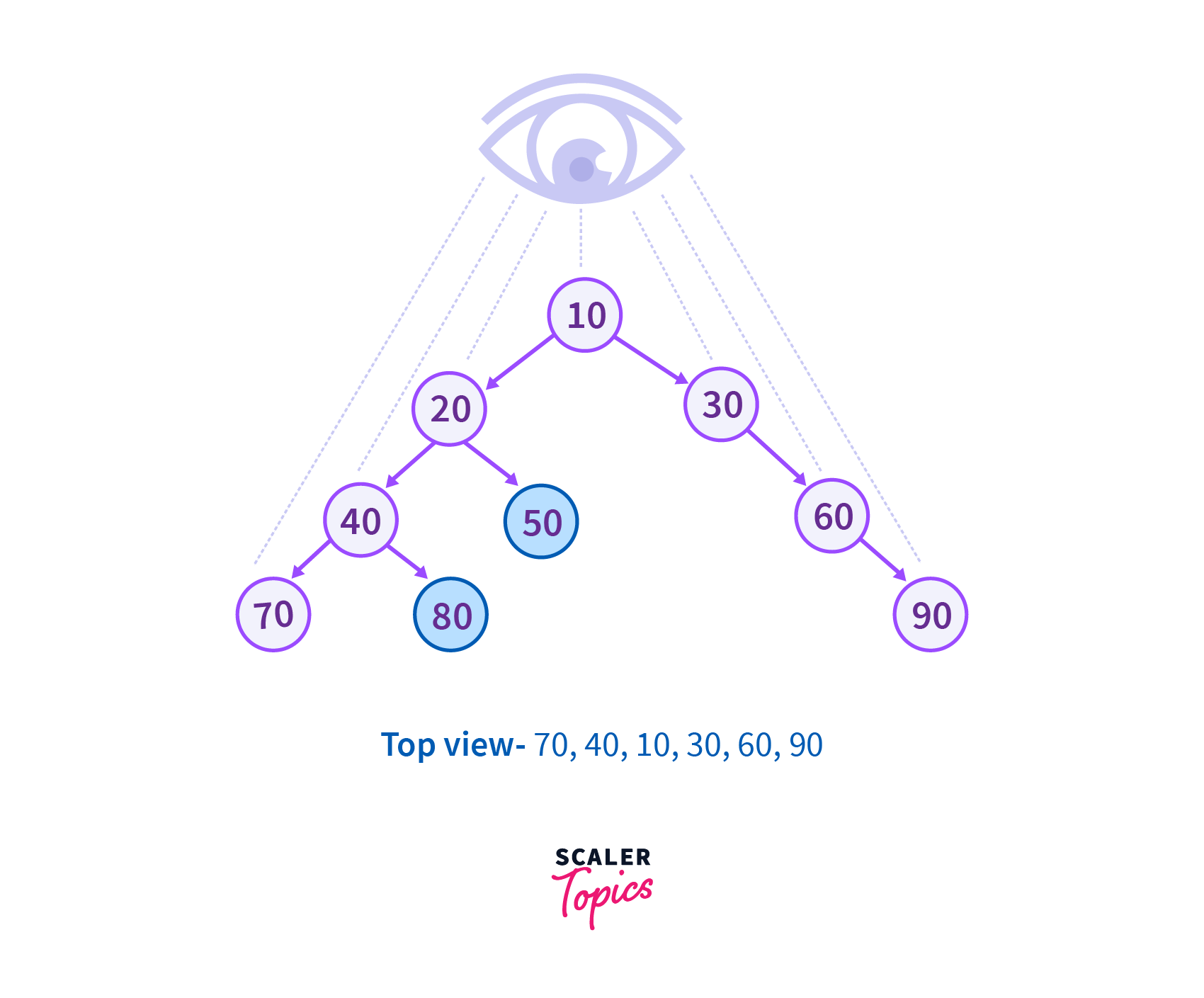
Solution for Top View of Binary Tree
Till this point, we have got a clear understanding of the problem. Now let us discuss the solution to this problem. The problem of printing the Top View of Binary Tree can be solved by using two methods which are as follows.
- Depth First Search
(DFS)/ Inorder Traversal - Breadth-first search
(BFS)/ Level order traversal
Now let us discuss these methods in great detail.
Depth First Search (DFS) / Inorder Traversal
- The idea is to perform the in-order traversal of the binary tree and the top view will consist of only those nodes which are having distinct values of either vertical height or horizontal width or both.
- In case of multiple nodes with the same values of vertical height or horizontal width we will use hashing so that we can check that the node with the current height or horizontal width is traversed the first time or has already been visited.
Illustration of the Above Approach
Below is the illustration of the above approach.
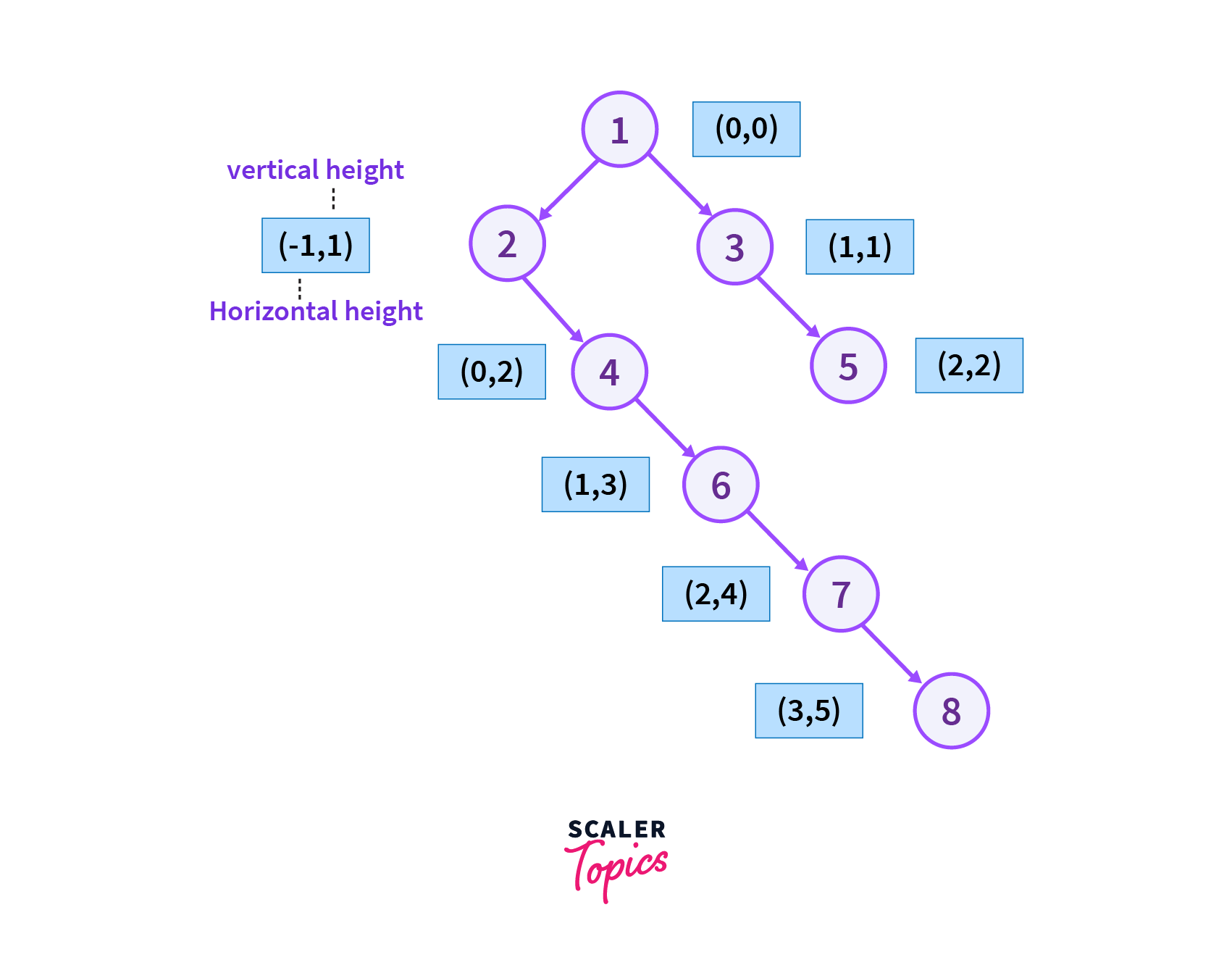
Consider the Tree with Eight vertices which is shown in the picture below. Here the (0,0) represents the vertical height and horizontal width of the root node respectively.
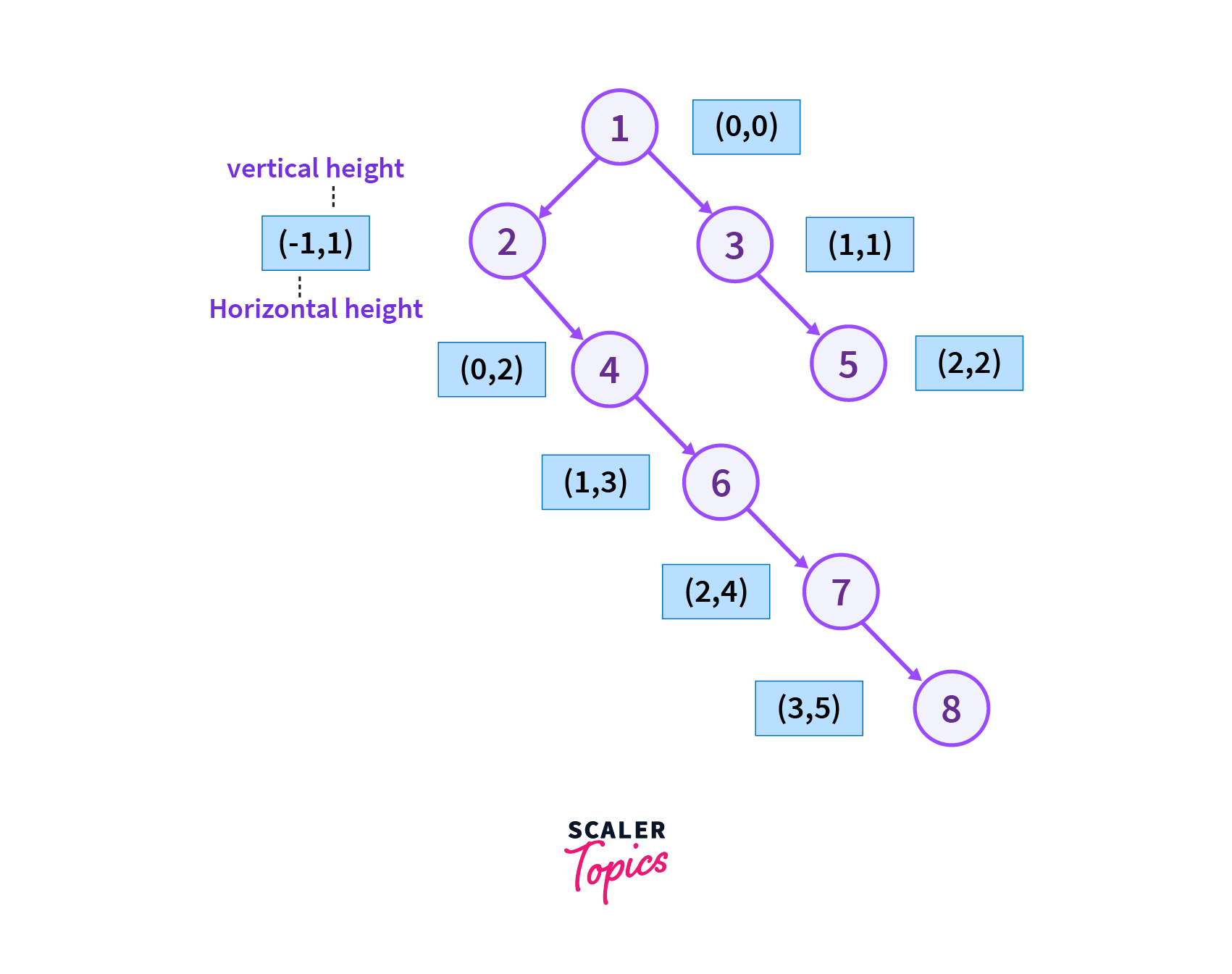
Step 1
We will start from the left vertex of vertex 1 which is vertex 2 as it is in order traversal of the binary tree and we also add the current vertex to the map.
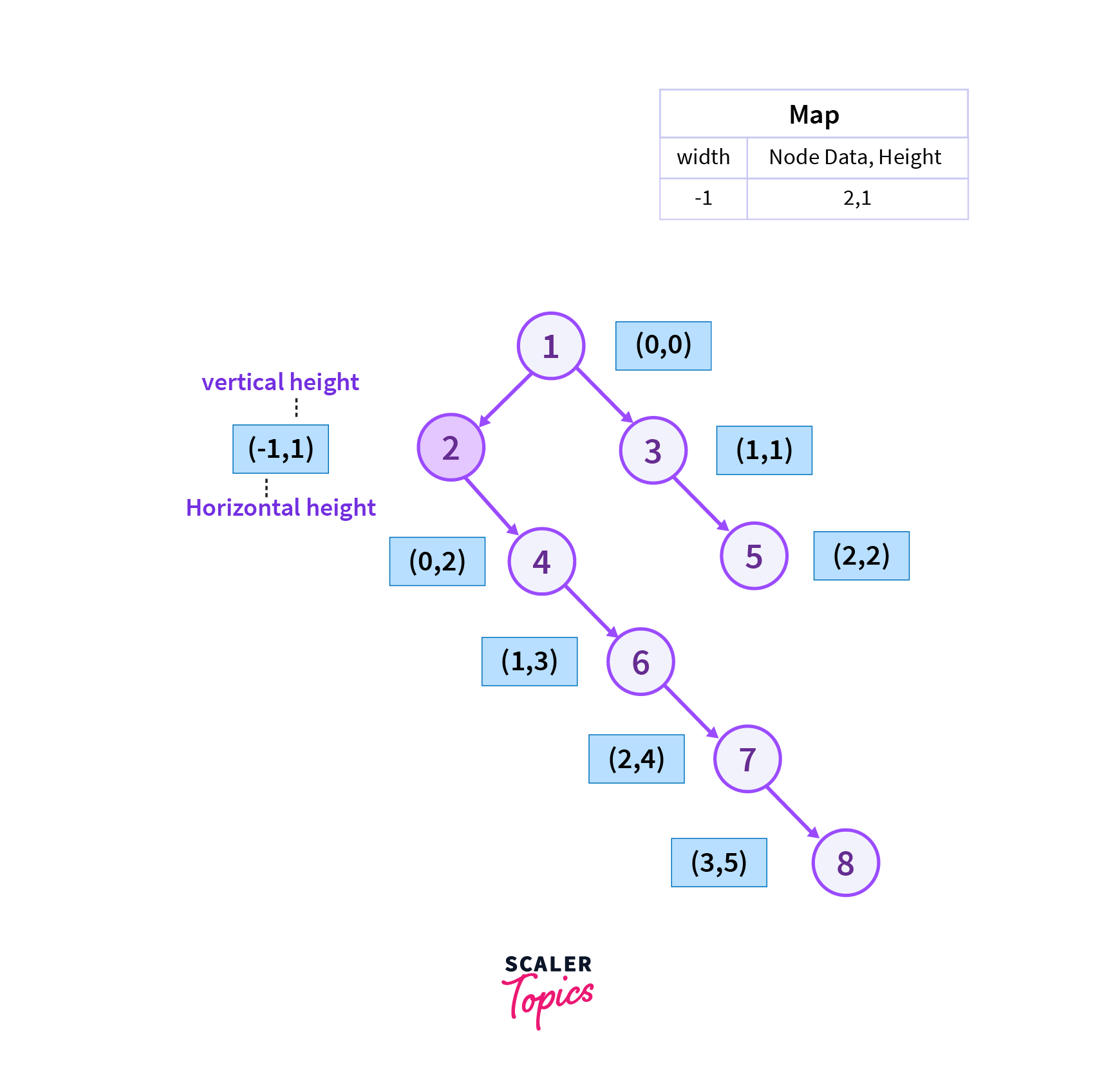
Step 2
We will move from the right vertex of vertex 2 which is vertex 4 as it is in order traversal of the binary tree and vertex 2 has no left child then we add the current vertex to the map.
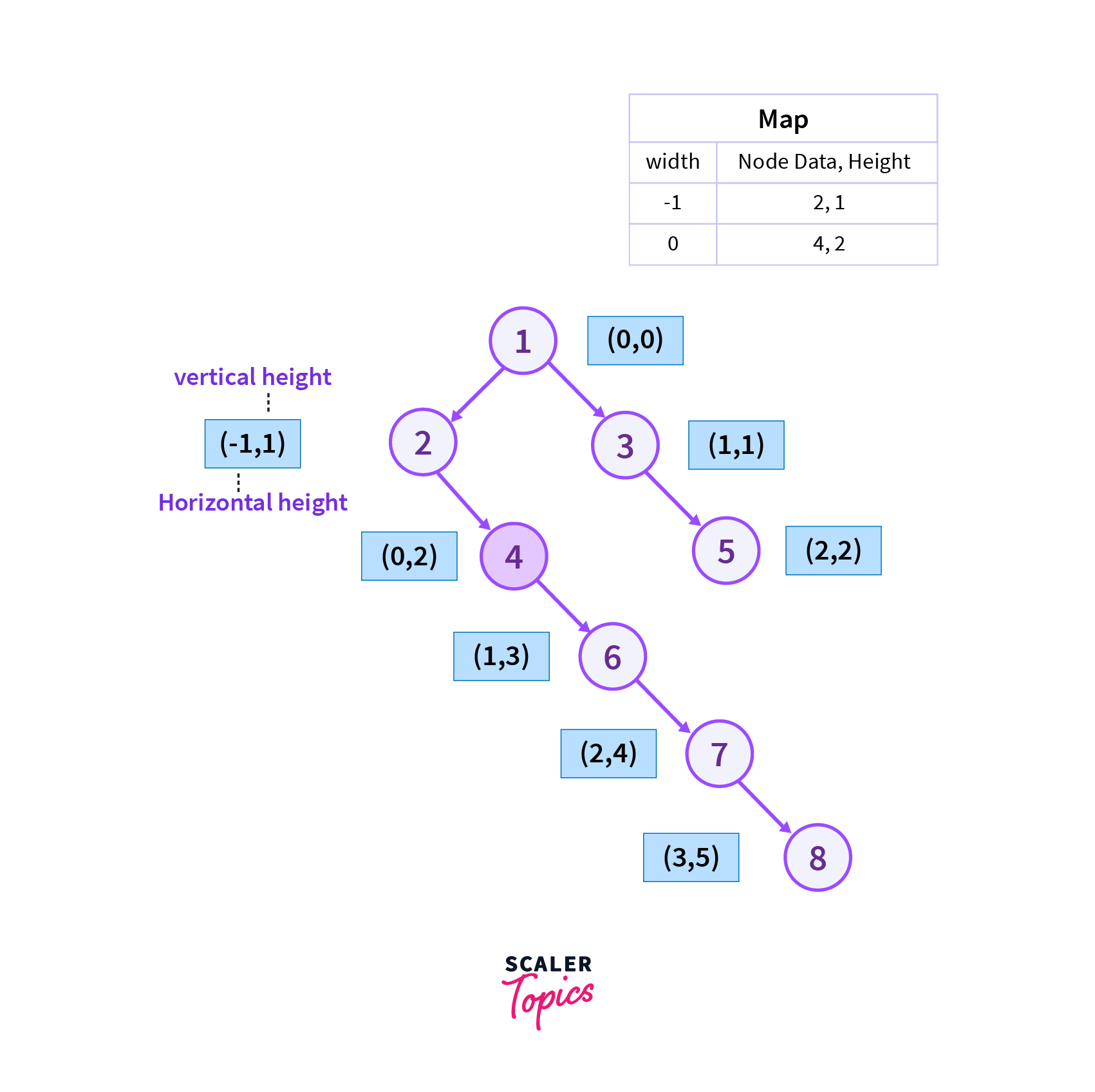
Step 3
We then move from the right vertex of vertex 4 which is vertex 6 as it is in order traversal of the binary tree and vertex 4 has no left child then we add the current vertex to the map.
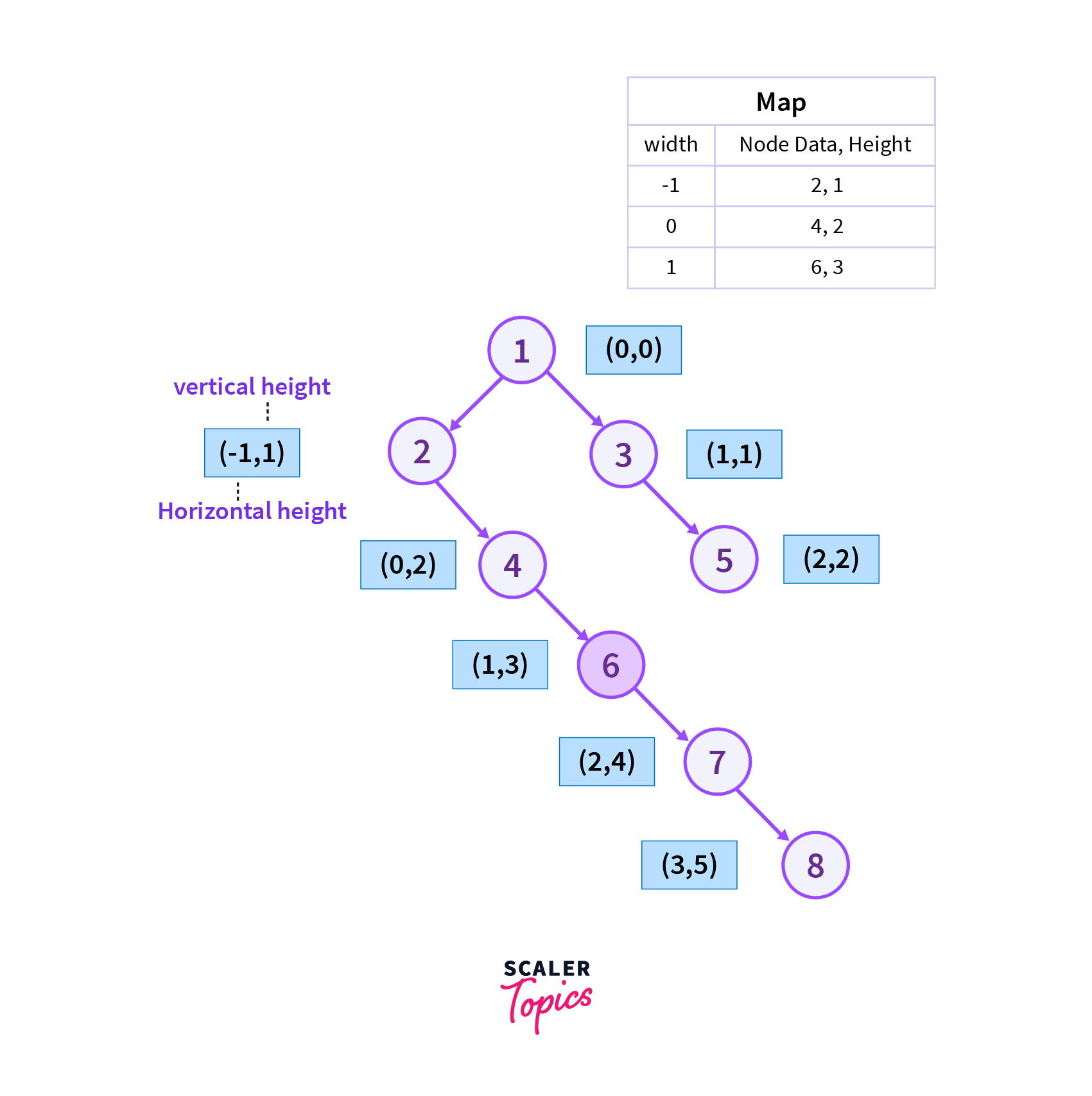
Step 4
We then move from the right vertex of vertex 6 which is vertex 7 as it is in order traversal of the binary tree and vertex 6 has no left child then we add the current vertex to map.
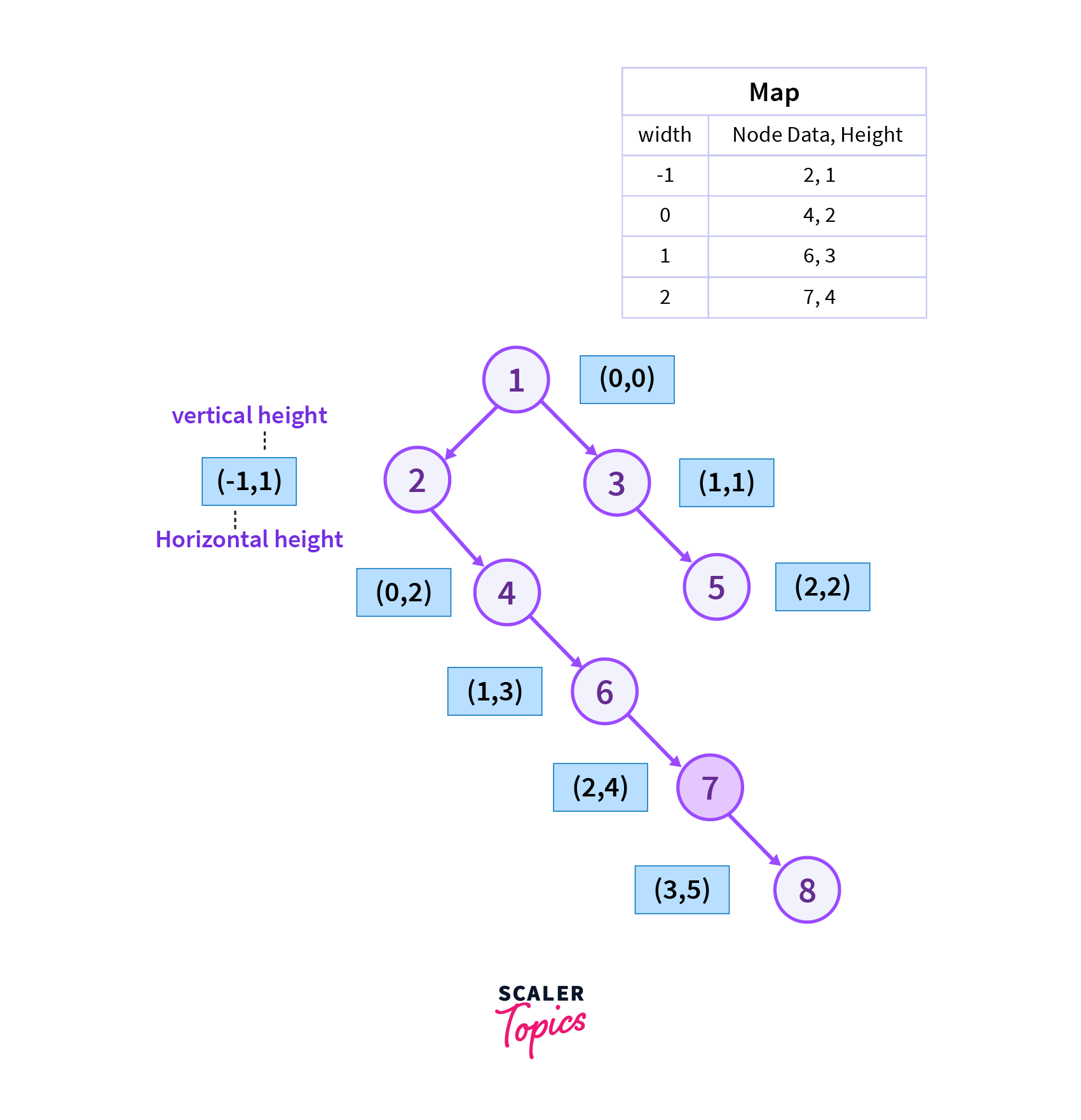
Step 5
We then move from the right vertex of vertex 7 which is vertex 8 as it is in order traversal of the binary tree and vertex 7 has no left child then we add the current vertex to the map.
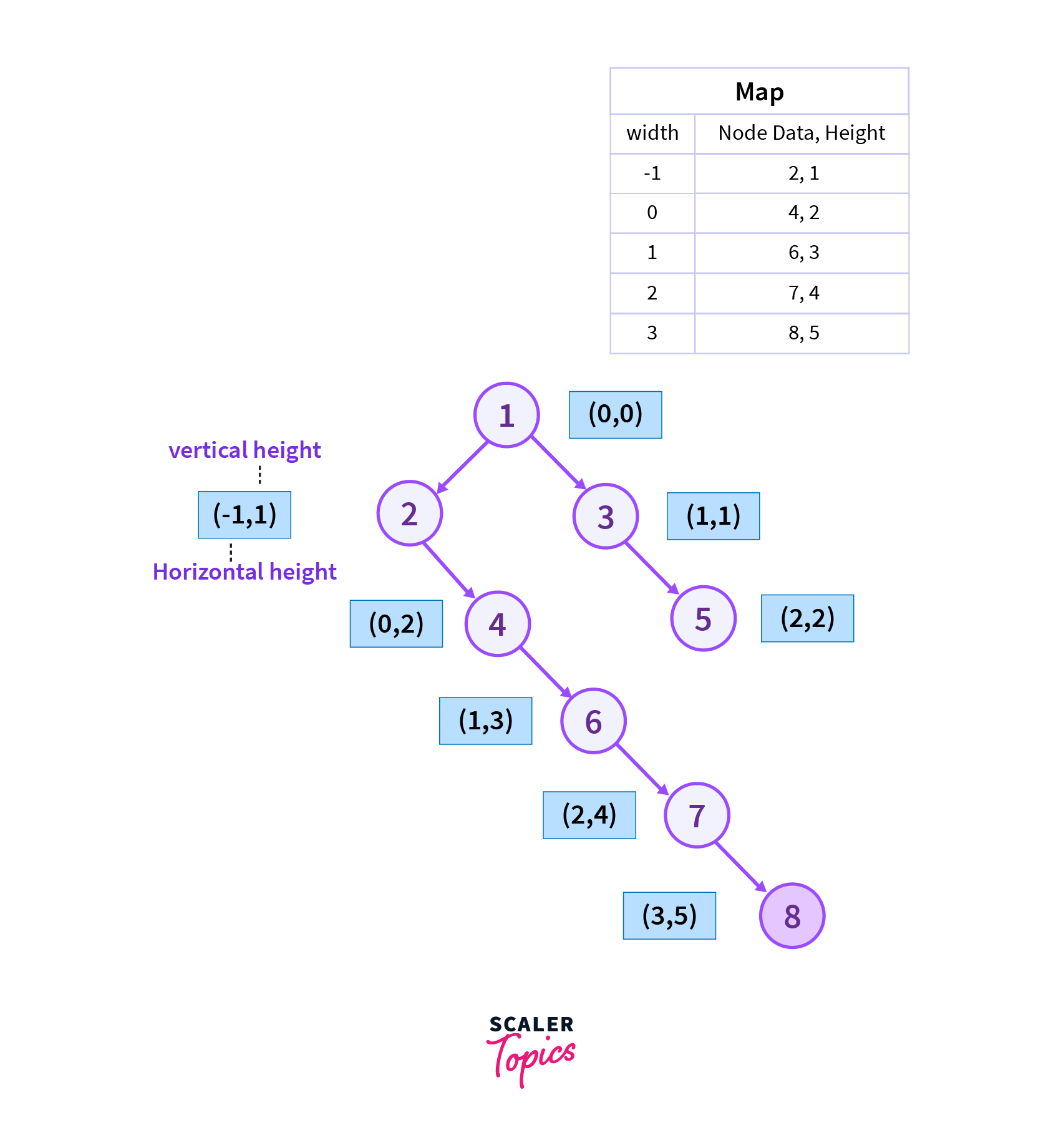
Step 6
Now we will move to the root which is vertex 1 and after reaching vertex 1 we found that the height of the current node vertex 1 is smaller than the height stored corresponding to the vertex with the same horizontal width in the map. So we update the height, data of the node with the height, and data of the current vertex.
Mathematically we can express the above situation as follows.
if (Map[current_widht]>current_node's_height)
Map[current_widht]=current_node's_data,current_node's_height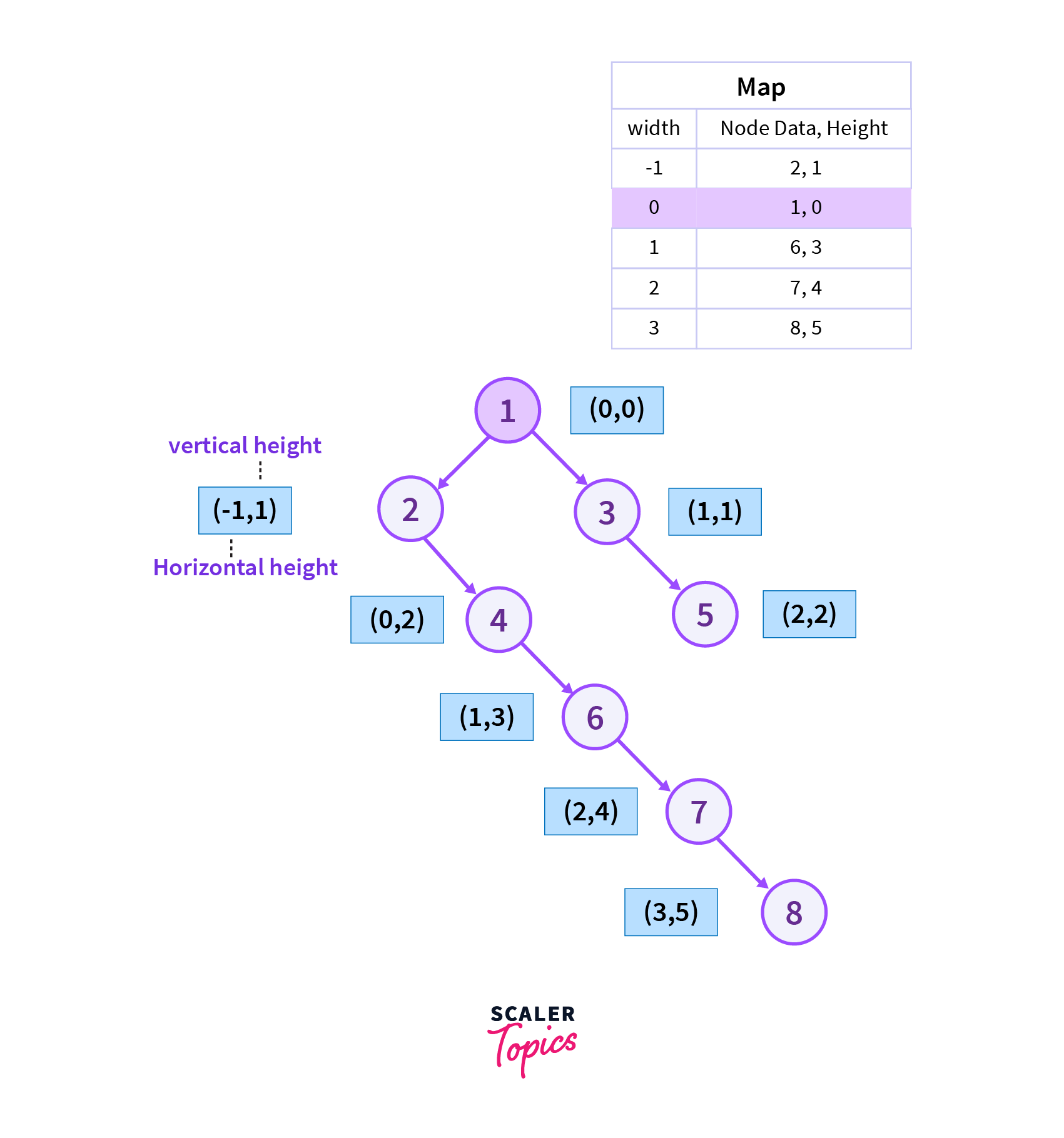
Step 7
Now we will move to the right of vertex 1 which is vertex 3 and after reaching vertex 3 we found that the height of a current node is smaller than the height stored corresponding to the vertex with the same horizontal width in the map. So we update the height, data of the node with the height, and
data of the current vertex.
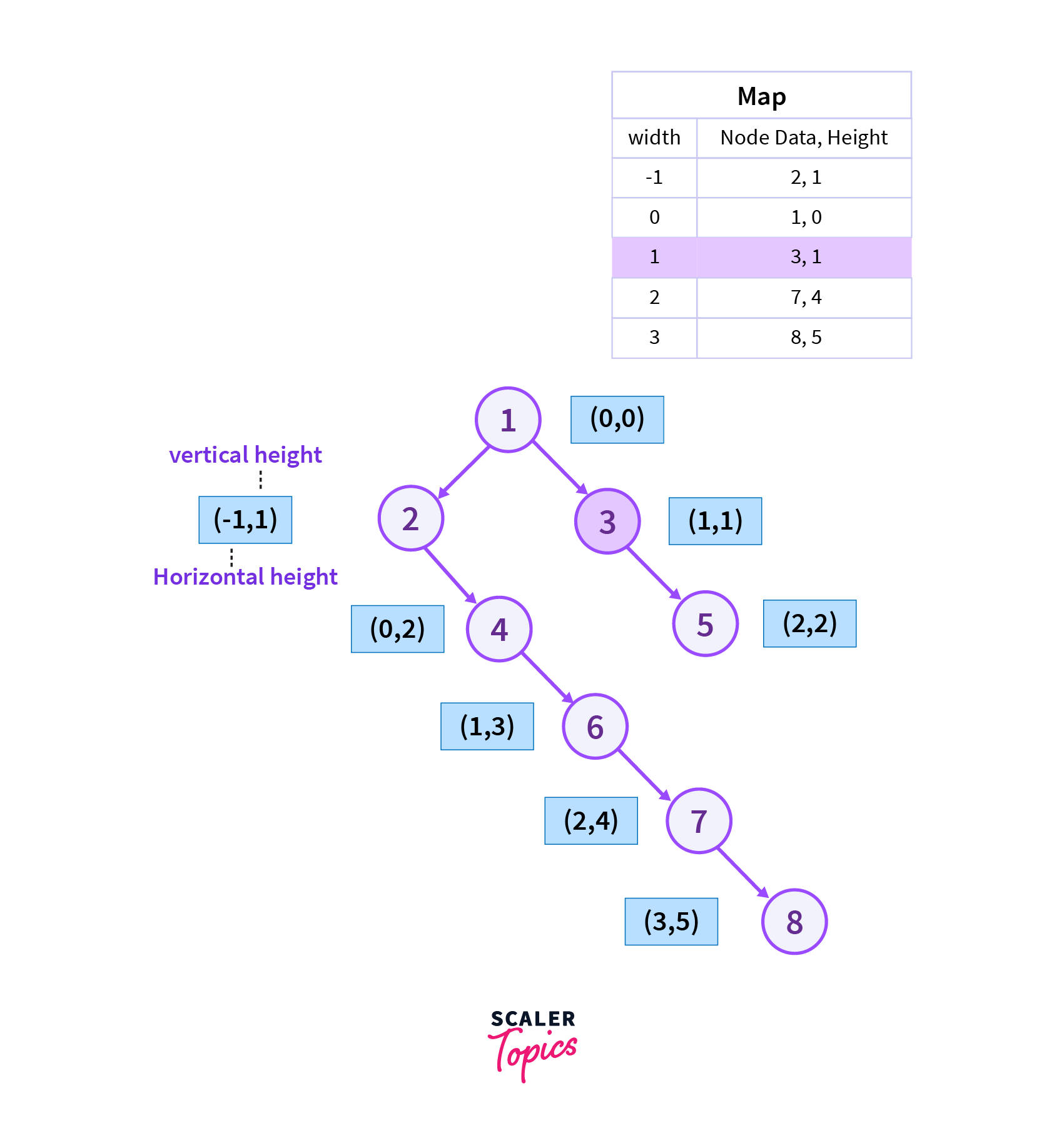
Step 8
Now we will move to the right of vertex 3 which is vertex 5 and after reaching vertex 5 we found that the height of a current node is smaller than the height stored corresponding to the vertex with the same horizontal width in the map. So we update the height, data of the node with the height, and data of the current vertex.
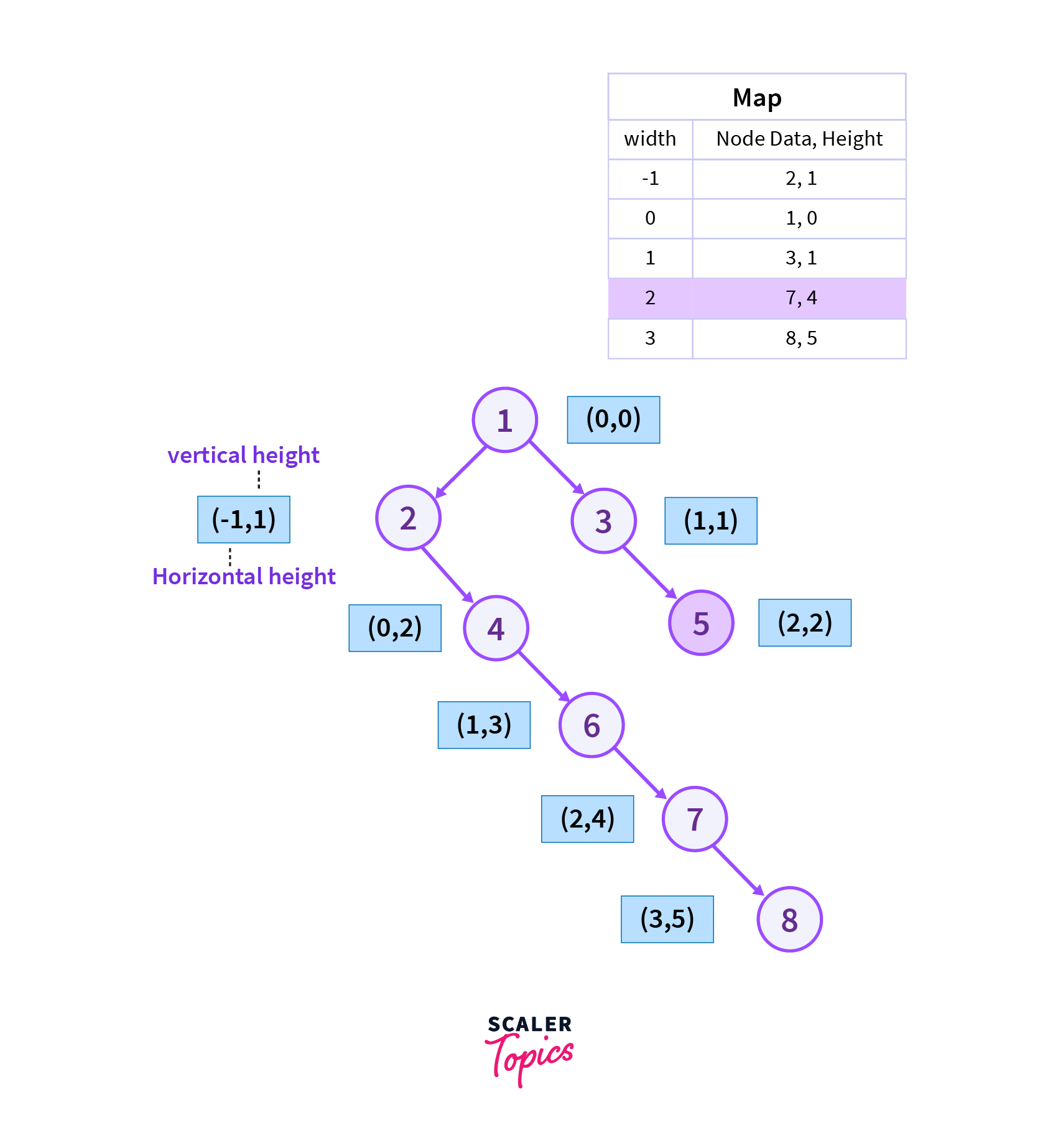
Below is the table which represents the set of vertices that we will traverse while finding the Top View of the Binary Tree.
| Width | Node data, Height |
|---|---|
| -1 | 2, 1 |
| 0 | 1, 0 |
| 1 | 3, 1 |
| 2 | 5, 2 |
| 3 | 8, 5 |
Algorithm to Implement the Above Approach
Below is the step by step approach to get the Top View of the Binary Tree using Depth First Search.
To implement the Top View of the Binary Tree we will follow the steps below.
- Firstly we will create a map to store the
top-viewof thebinary tree. - Then our idea is to perform inorder traversal of the
binary tree. - During the inorder traversal we will keep track of vertical height(h) and horizontal width(w) of each node of the
binary tree. - For the current node we will check if it’s horizontal width level has been visited or not.
- If the current horizontal level has not been visited then, map the {current horizontal width -> (current node data,current vertical height)}.
- We can write the above statement in form of expression below. Map[Horizontal Width -> (Node.data,Vertical Height)]
- If a particular horizontal width level has been visited, then we check for the vertical height which is mapped to that horizontal width.
- If the vertical height of a current node is less than the mapped vertical height, it simply means that the current node lies vertically above the previously mapped node and hence it will be included in the top view of the binary tree then we simply update the mapped value of current horizontal width with the horizontal height of the current node.
- Finally after the complete traversal of the binary tree, we simply output the top view node values in order of their horizontal levels.
Implementation of the Above Algorithm
- Create a map to store the data and horizontal distance (Level) of each node.
- While performing the
Inorder Traversalof the binary tree check if a particular horizontal level has been visited or not. - We can check whether a particular leval has been visited or not just by checking if the entry corresponding to the current width is present in the map or not.
- If it is not present in the map then we insert it into the map.
- If a particular horizontal level has already been visited then we check if the height of the current node is less than the previous node at the same horizontal level.
- For a particular level if it is already visited then we replace the height of the previous node with the height of the current node in the top view of the binary tree.
Below is the C++ Program to find the Top View of the Binary Tree.
#include <bits/stdc++.h>
using namespace std;
// Node class representing the tree node
class Node
{
public :
int data;
Node *left;
Node *right;
// Constructor to initialize the Node class
Node(int x)
{
data = x;
left = right = NULL;
}
};
void Inorder_Traversal(Node *root,int width,int height, map<int,pair<int,int>> &m)
{
if(root == NULL)
return;
Inorder_Traversal(root->left,width-1,height+1,m);
/* If the current horizontal level has not been visited yet
then we insert it into the map */
if(m.find(width) == m.end())
m[width] = make_pair(root->data,height);
// If for the current node, current level
// is already visited and its height is
// less than the height of the
// previous node then we update the
// height with the height of current node
else if(m[width].second>height)
m[width] = make_pair(root->data,height);
Inorder_Traversal(root->right,width+1,height+1,m);
}
/* Function to print
the Top_Viewiew of
the binary tree */
void Print_Top_View(Node *root)
{
if(root == NULL)
return;
// create a map to store data, height
// and width of the current node.
map<int,pair<int,int>> m;
// While perfrming Inorder_Traversal store
// the nodes that represent the Top View of
// binary tree into the map
Inorder_Traversal(root,0,0,m);
/* Traverse the map and print top view of the binary tree */
cout<<"Top View Nodes\n";
for(auto it : m)
cout<<it.second.first<<" ";
}
int main()
{
Node *root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->right->right = new Node(7);
root->left->right = new Node(5);
root->left->right->right = new Node(9);
root->left->left = new Node(4);
root->left->left->left = new Node(8);
root->right->right->right = new Node(10);
Print_Top_View(root);
return 0;
}Input For the Above Program
The nodes with yellow colour are the part of top view of the tree.
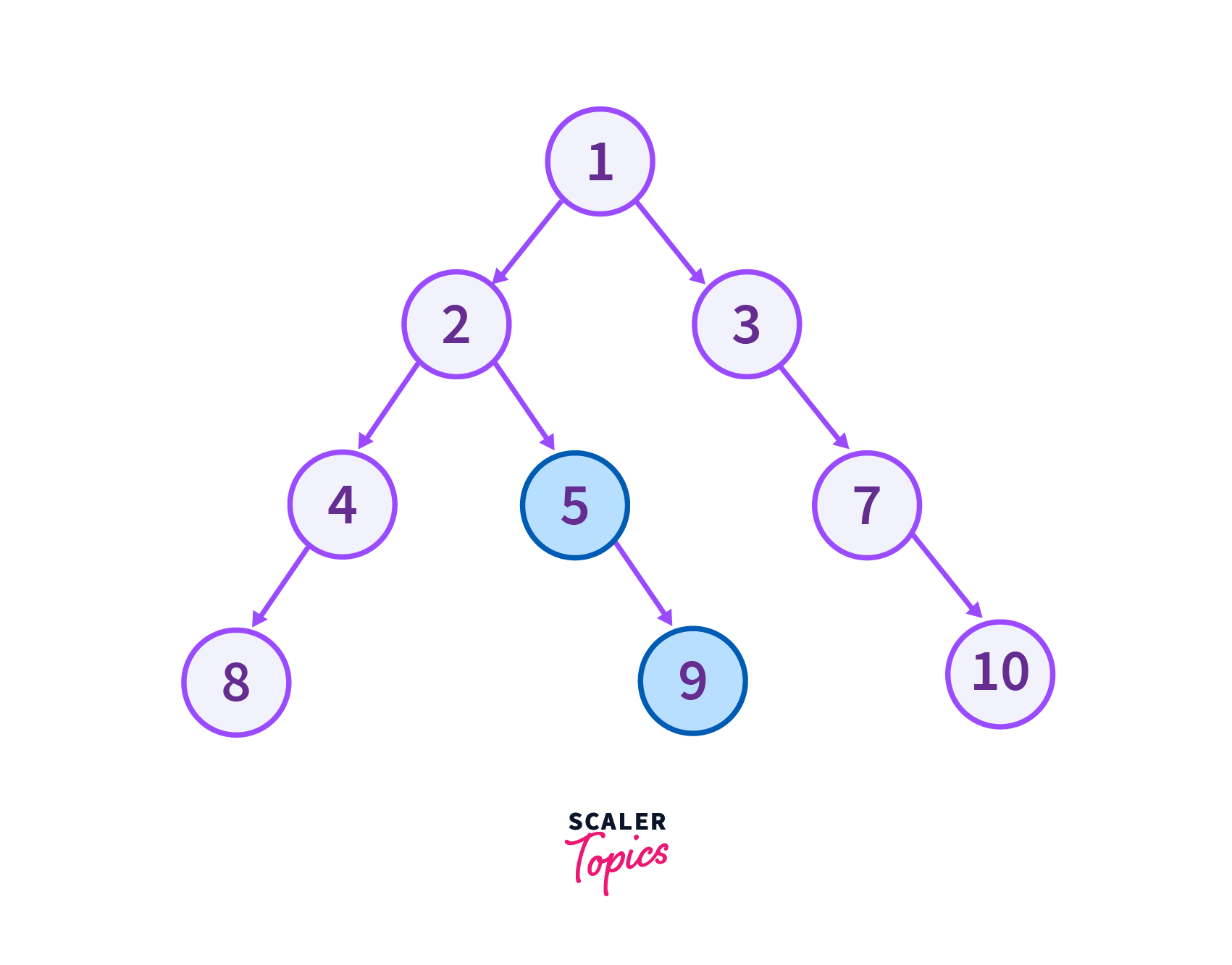
Output of the above program
> Top View Nodes
8 4 2 1 3 7 10 :::
:::section{.main}
Breadth First Search (BFS) / Level Order Traversal
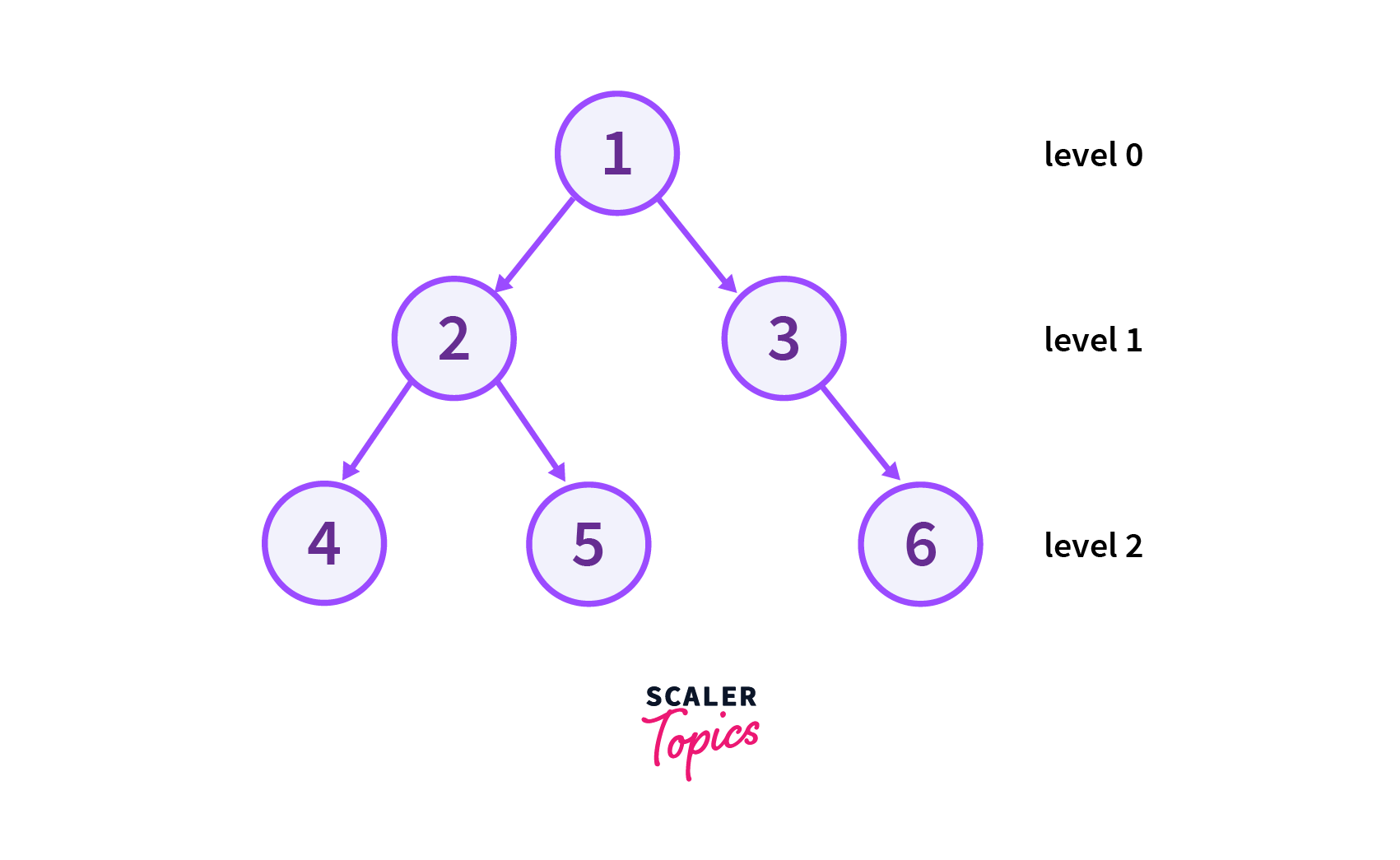
The idea is to perform the Breadth-First Search Traversal of the binary tree. Whenever we perform the BFS traversal of the binary tree, a particular horizontal level of the tree (Level 0 in above image) is traversed before all the horizontal levels ( in above image) which are below the current level. So, in such case, we don’t have to keep track of height for all the nodes of the binary tree.
In other words, we can say that instead of keeping track of height for all the nodes of a binary tree, we simply track the horizontal depth/width of each of the tree nodes.
while performing the Breadth-First Traversal of the binary tree we check, if the horizontal width of the current node has not been visited then we simply map the current horizontal level to data of the current node. We can store this mapping into a treemap.
Finally, after the complete traversal of the binary tree, we simply output the top view stored in the map.
Illustration of the Above Approach
Below is the illustration of the above approach.
Consider the Tree with Eight vertices which is shown in the picture below. Here (0,0) represents the horizontal width and the vertical of the root node which is node 1.
Step 1
We will start from the root vertex which is vertex 1 as it is the Level Order traversal of the binary tree and we also add the current vertex to the map.
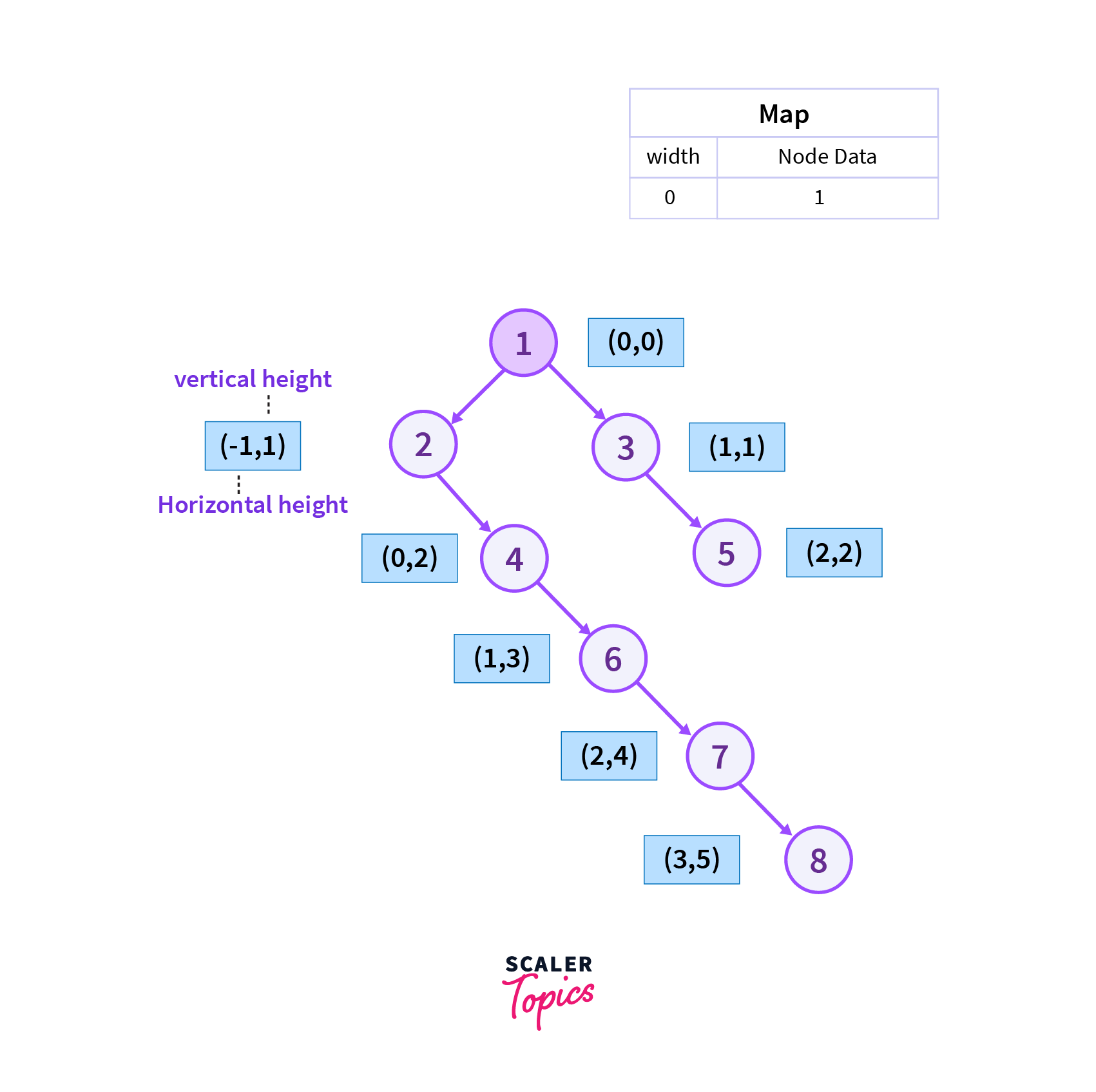
Step 2
Then we will move to the left of vertex 1 which is vertex 2 as it is Level Order traversal of the binary tree and we also add the current vertex to the map.
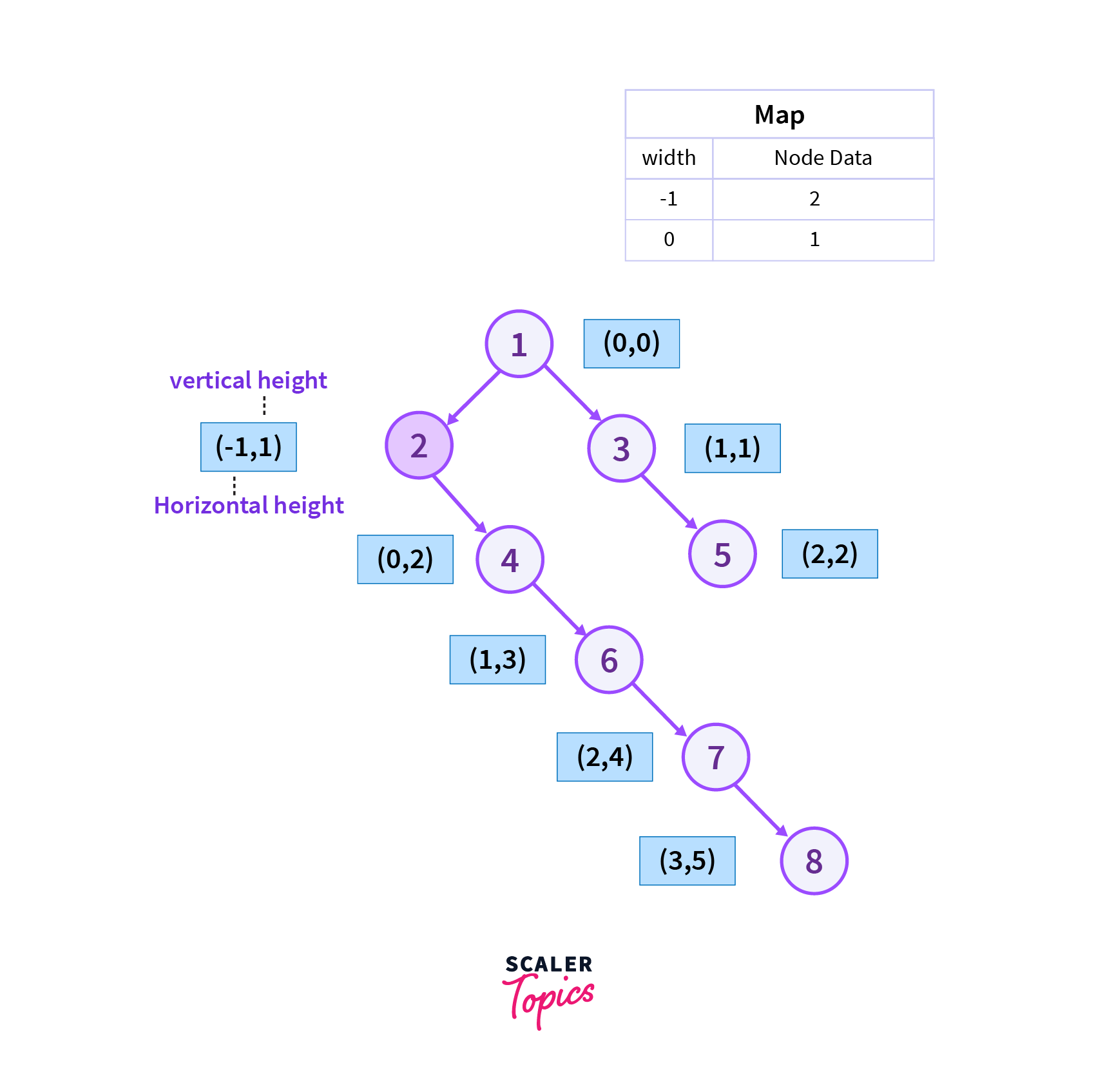
Step 3
Now we will move to the right of vertex 1 which is vertex 3 as it is the Level Order traversal of the binary tree and we also add the current vertex to the map.
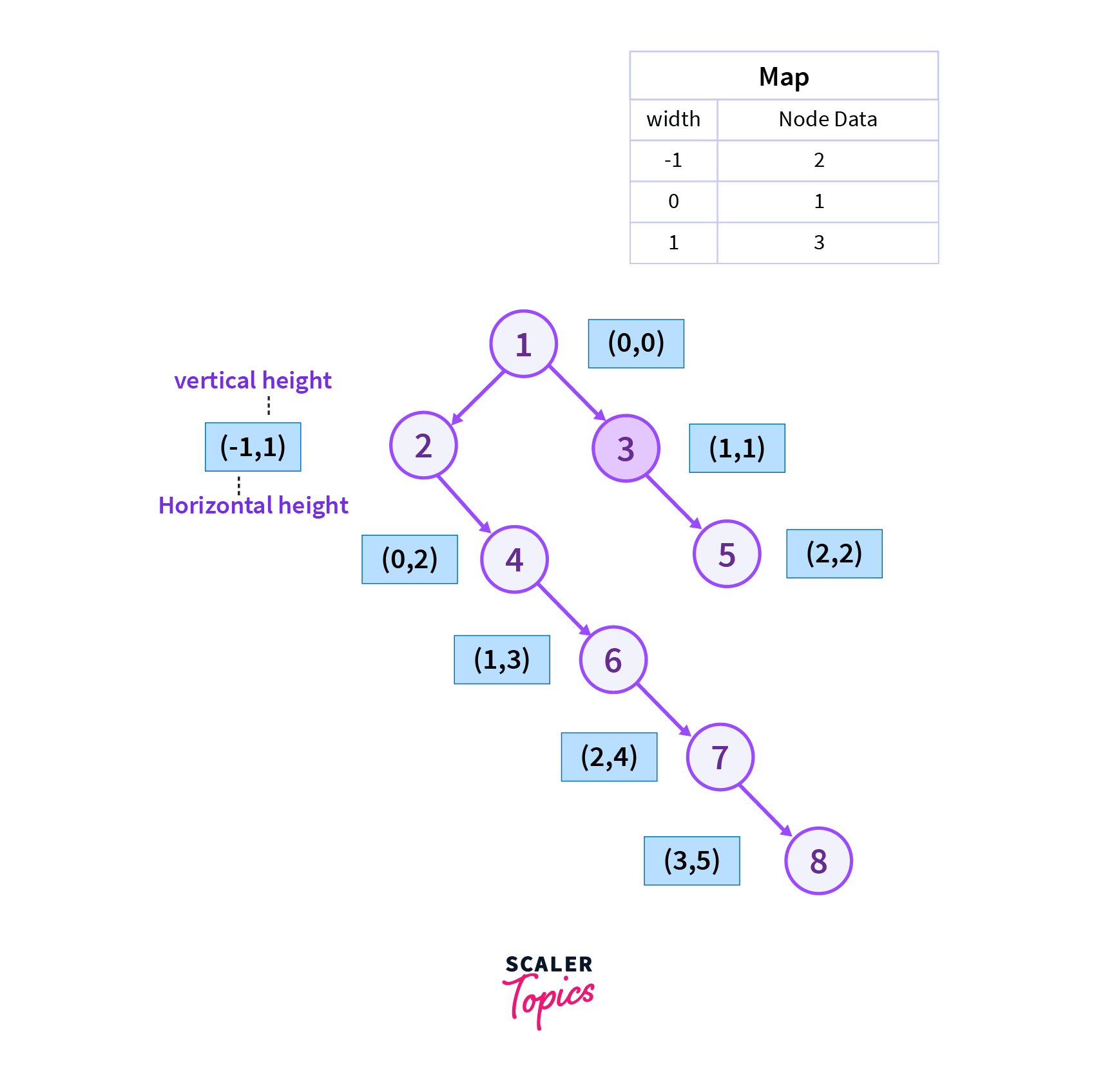
Step 4
Since the immediate left and right children of vertex 1 are visited so now we will move to the right of vertex 2 which is vertex 4 we can also observe that the horizontal width w=0 is already present in the map so we don’t need to replace we are using this logic in order to avoid the vertices from being stored in the map which are not the part of our top view of the binary tree.
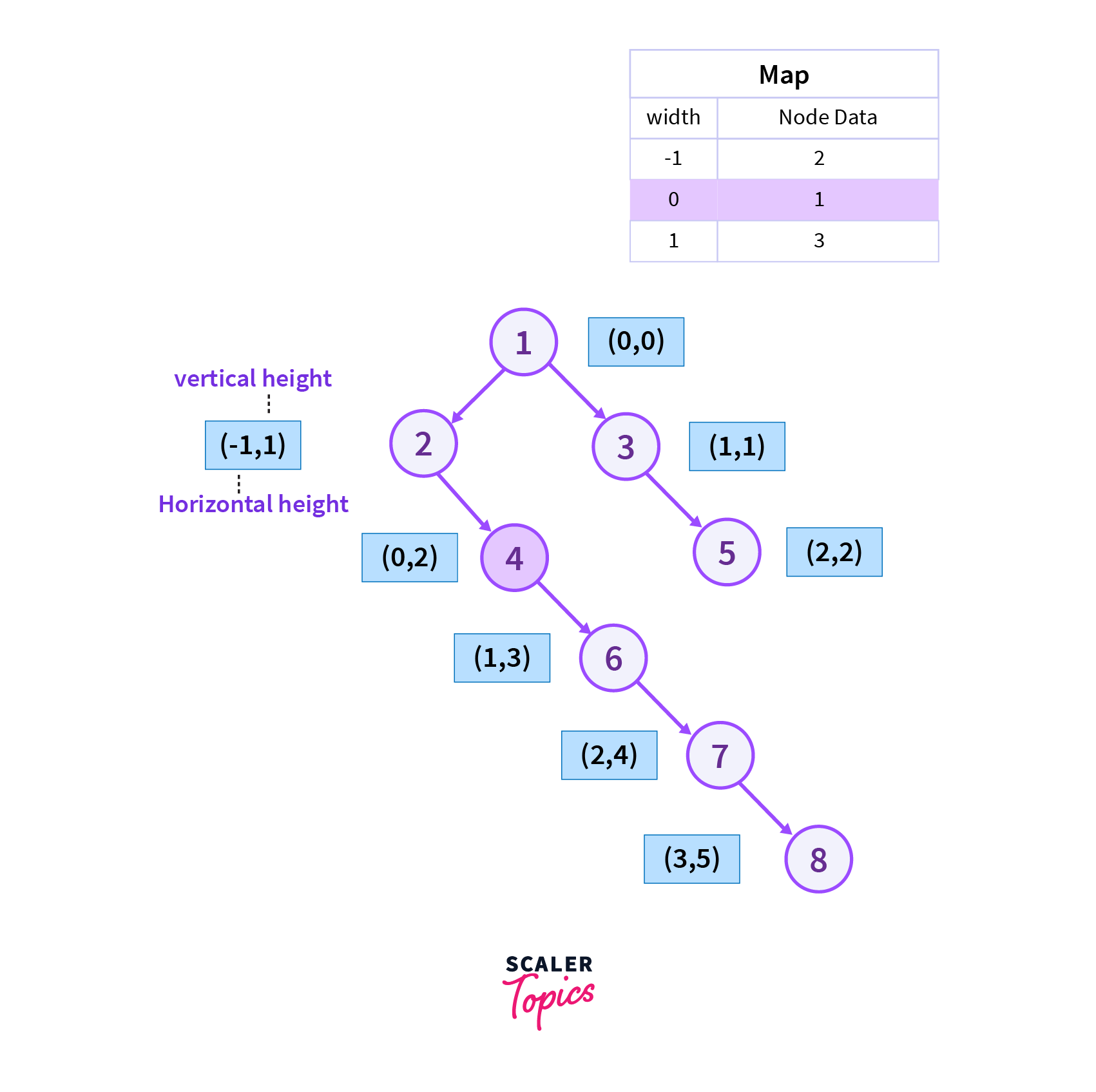
Step 5
Now we will move to the right of vertex 3 which is vertex 5 as it is the Level Order traversal of the binary tree and we also add the current vertex to the map.
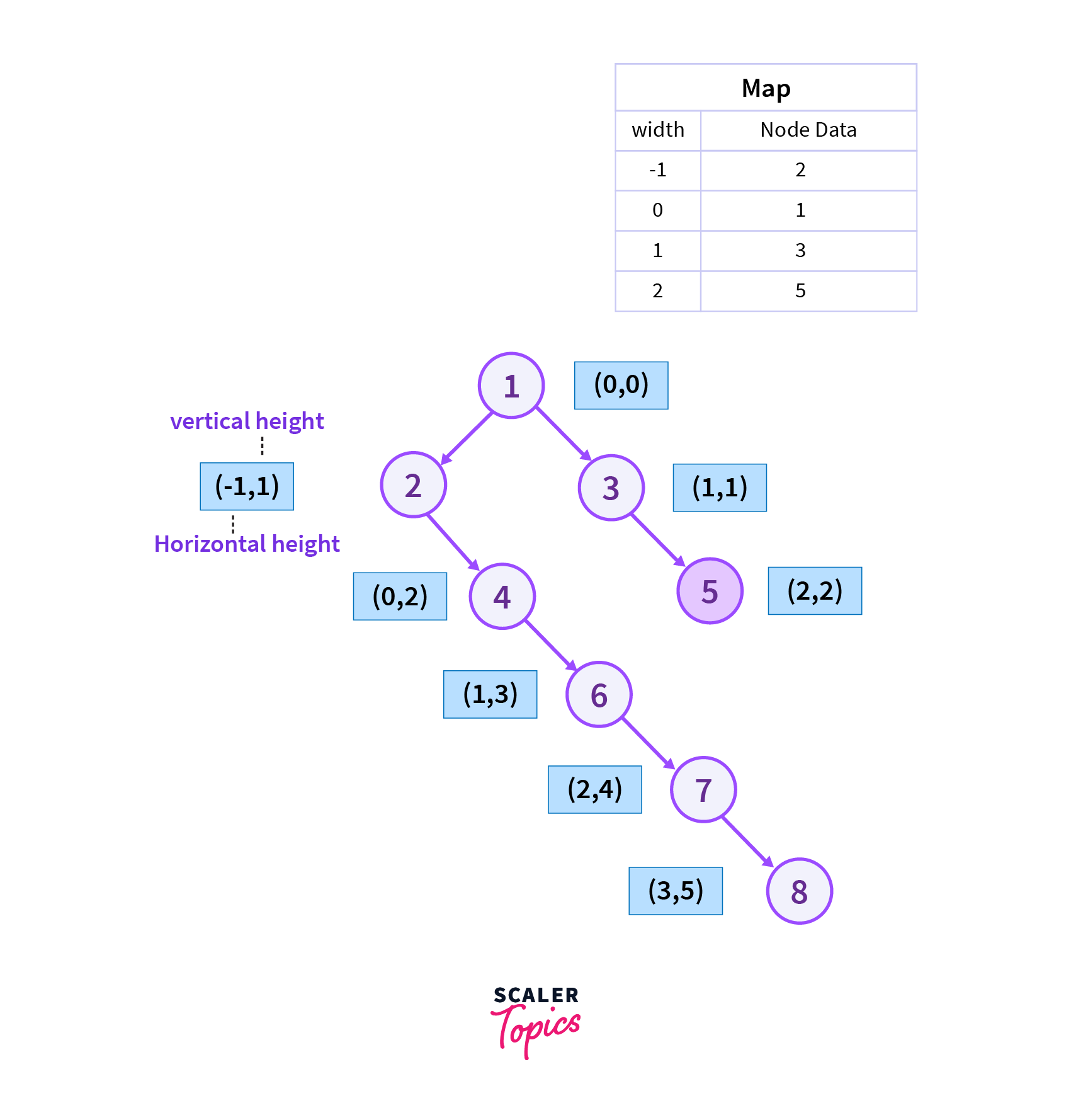
Step 6
Since the immediate left and right children of vertex 5 are visited so now we will move to the right of vertex 4 which is vertex 6 we can also observe that the horizontal width w=1 is already present in the map so we don’t need to replace we are using this logic in order to avoid the vertices from being stored in the map which are not the part of our top view of the binary tree.
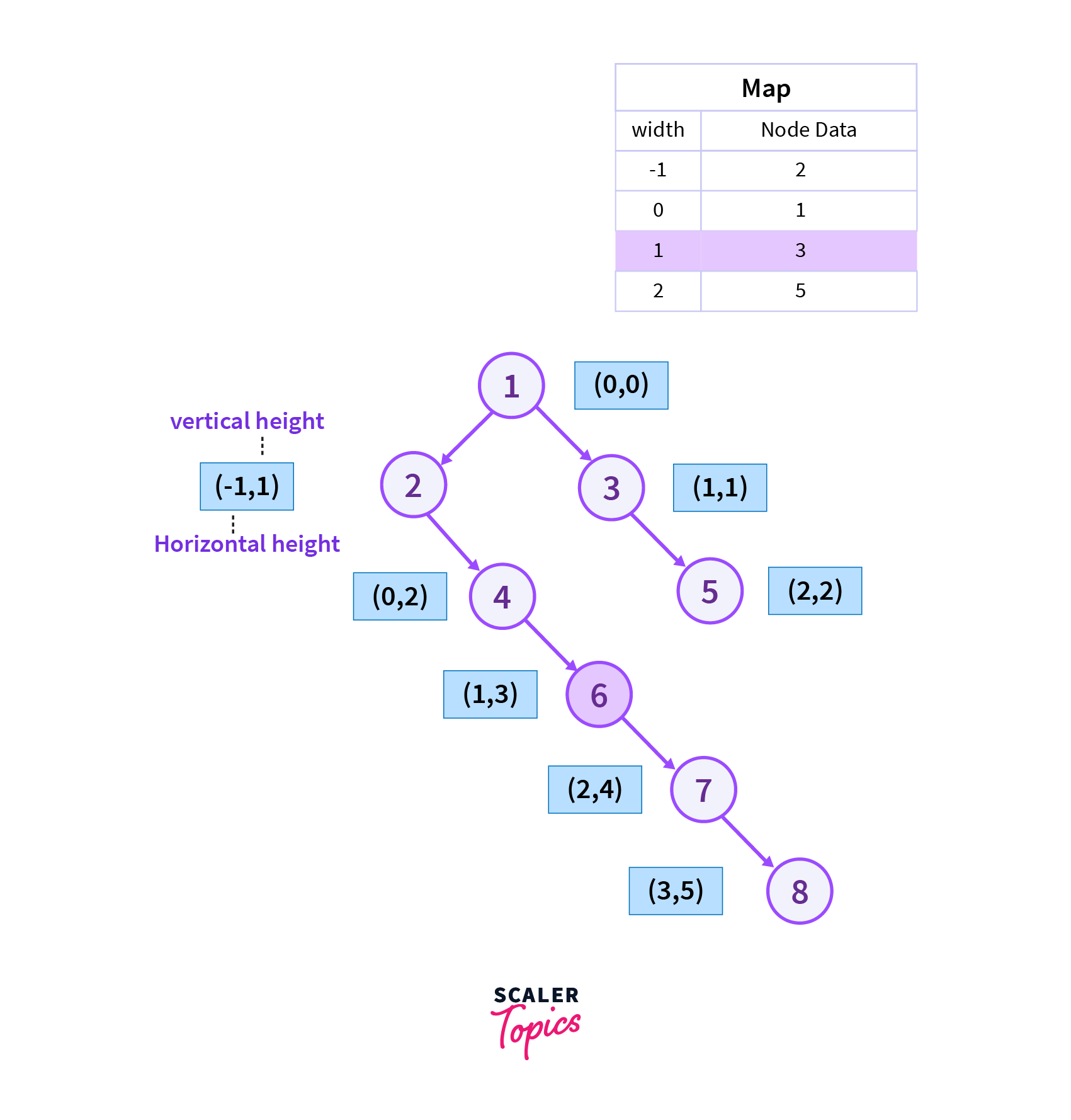
Step 7
Since the immediate left and right children of vertex 5 are visited so now we will move to the right of vertex 4 which is vertex 7 we can also observe that the horizontal width w=2 is already present in the map so we don’t need to replace.
We are using this logic in order to avoid the vertices from being stored in the map which are not part of our top view of the binary tree.
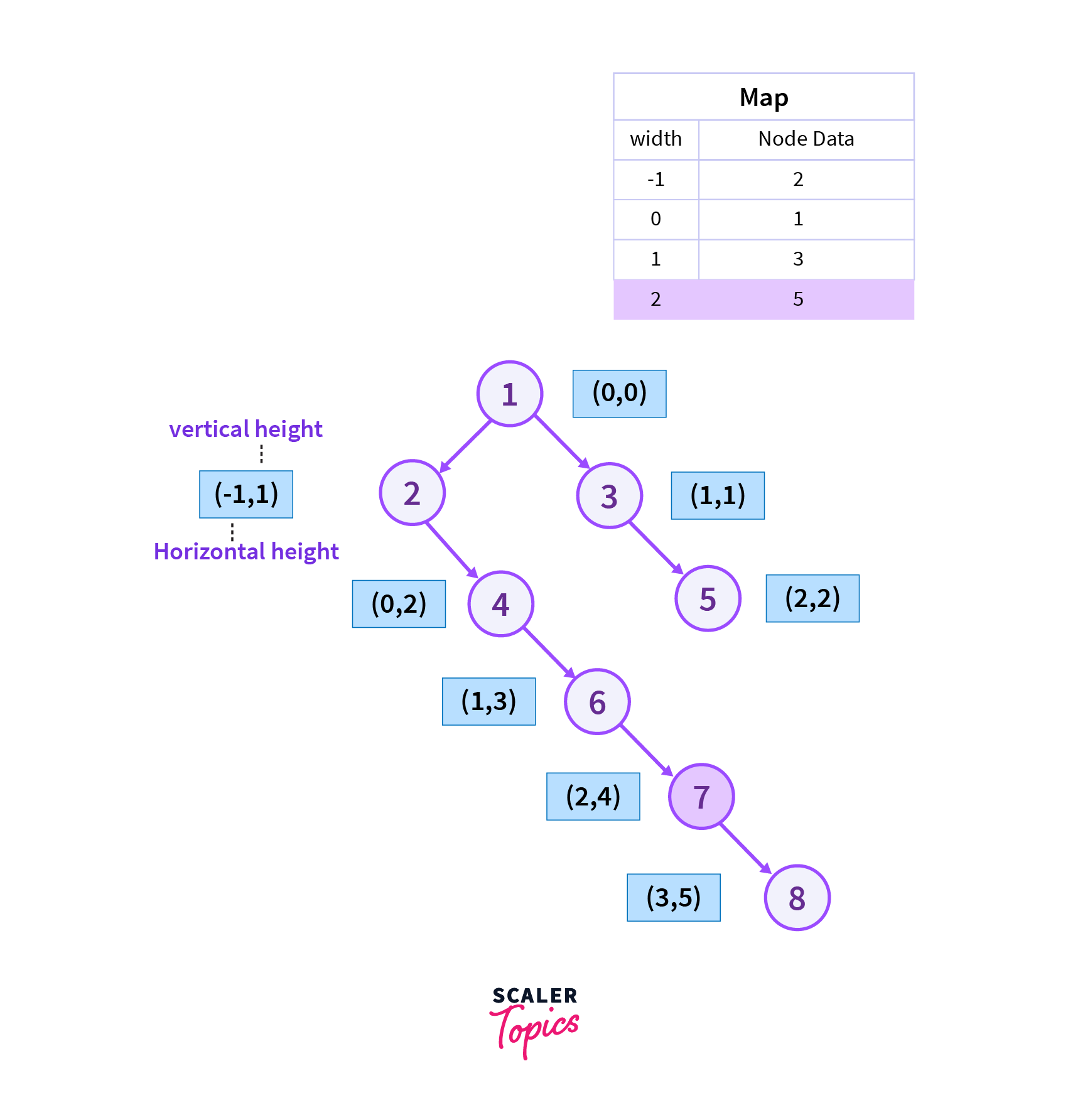
Step 8
Now we will move to the right of vertex 7 which is vertex 8 as it is the Level Order traversal of the binary tree and we also add the current vertex to the map.
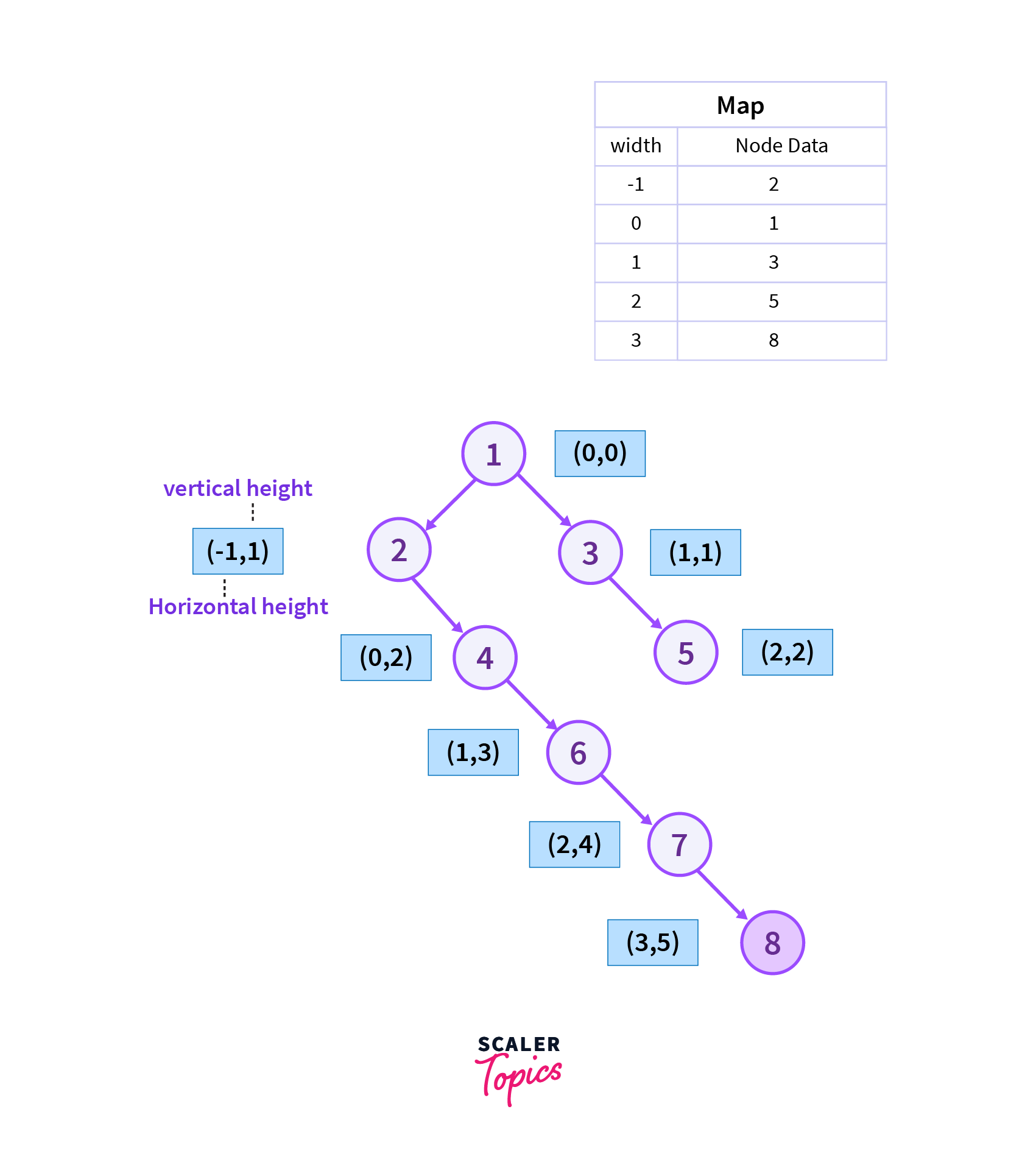
Below is the table which represents the set of vertices which we will traverse while finding the Top View of the Binary Tree.
| Width | Node data |
|---|---|
| -1 | 2 |
| 0 | 1 |
| 1 | 5 |
| 2 | 5 |
| 3 |
Algorithm to implement the above Approach
Below is the step by step approach to get the Top View of the Binary Tree using Breadth-First Search.
- Firstly we create a queue and we will use that queue to store the nodes of the binary tree and their corresponding horizontal widths.
- In order to store the top view of the binary tree we create a map where the key of the map represents the horizontal width which is mapped to the value which is actually the data of the node of the binary tree.
- Now we perform the
BFStraversal of the given binary tree. - For the node which is visited currently, we will check if it’s horizontal width has already been visited already or not.
- For the currently visited node if its horizontal width is being visited for the first time, then simply map the current horizontal width to the data of the current node.
- Finally after the complete traversal, we simply output the top view which is stored in the map.
Implementation of the Above Algorithm
- Create a map to store the horizontal width and value of each node which is to be included in the top view.
- Create a queue to store the data of Node and its current Level
- Insert the root node into the queue.
- Pop out every element of the queue one by one.
- Check for each element of the queue
- If the current horizontal Level has not been visited then then add the first node which is encountered at this horizontal level during level order traversal to the map.
- Also check for the left and right child of the current node.
- Below is the C++ Program to find the Top View of Binary Tree.
#include <bits/stdc++.h>
using namespace std;
// Node class representing the tree node
class Node
{
public:
int data;
Node *left;
Node *right;
// Constructor to initialize the Node class
Node(int x)
{
data = x;
left = right = NULL;
}
};
// Function to print the nodes which are
// the part of top-view of the binary tree
void Print_Top_View(Node *root)
{
if(root == NULL)
return;
// create a map to store data
// and width of the current node.
map<int,int> m;
// Create a queue to store the data of Node and its current Level
queue<pair<Node*,int>> queue;
// Insert the root node into the queue
queue.push({root,0});
// Store the top view of binary tree
// into the Map
// Pop out every element of the queue one by one
while(!queue.empty())
{
auto Top = queue.front();
queue.pop();
Node *current = Top.first;
int horizontal_width = Top.second;
// if the current horizontal Level has not been
// visited then we include the first node which is
// encountered at this horizontal level
if(m.find(horizontal_width) == m.end())
m[horizontal_width] = current->data;
// Also check for the left and right child of the current node.
if(current->left)
queue.push({current->left,horizontal_width-1});
if(current->right)
queue.push({current->right,horizontal_width+1});
}
// print the top view of the Binary Tree
cout<<"Top View Nodes\n";
for(auto it : m)
cout<<it.second<<" ";
}
int main()
{
Node *root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->right->right = new Node(7);
root->left->right = new Node(5);
root->left->right->right = new Node(9);
root->left->left = new Node(4);
root->left->left->left = new Node(8);
root->right->left = new Node(6);
root->right->right = new Node(7);
root->right->right->right = new Node(10);
Print_Top_View(root);
return 0;
}Input For the Above Program
The nodes with yellow colour are the part of top view of the tree.
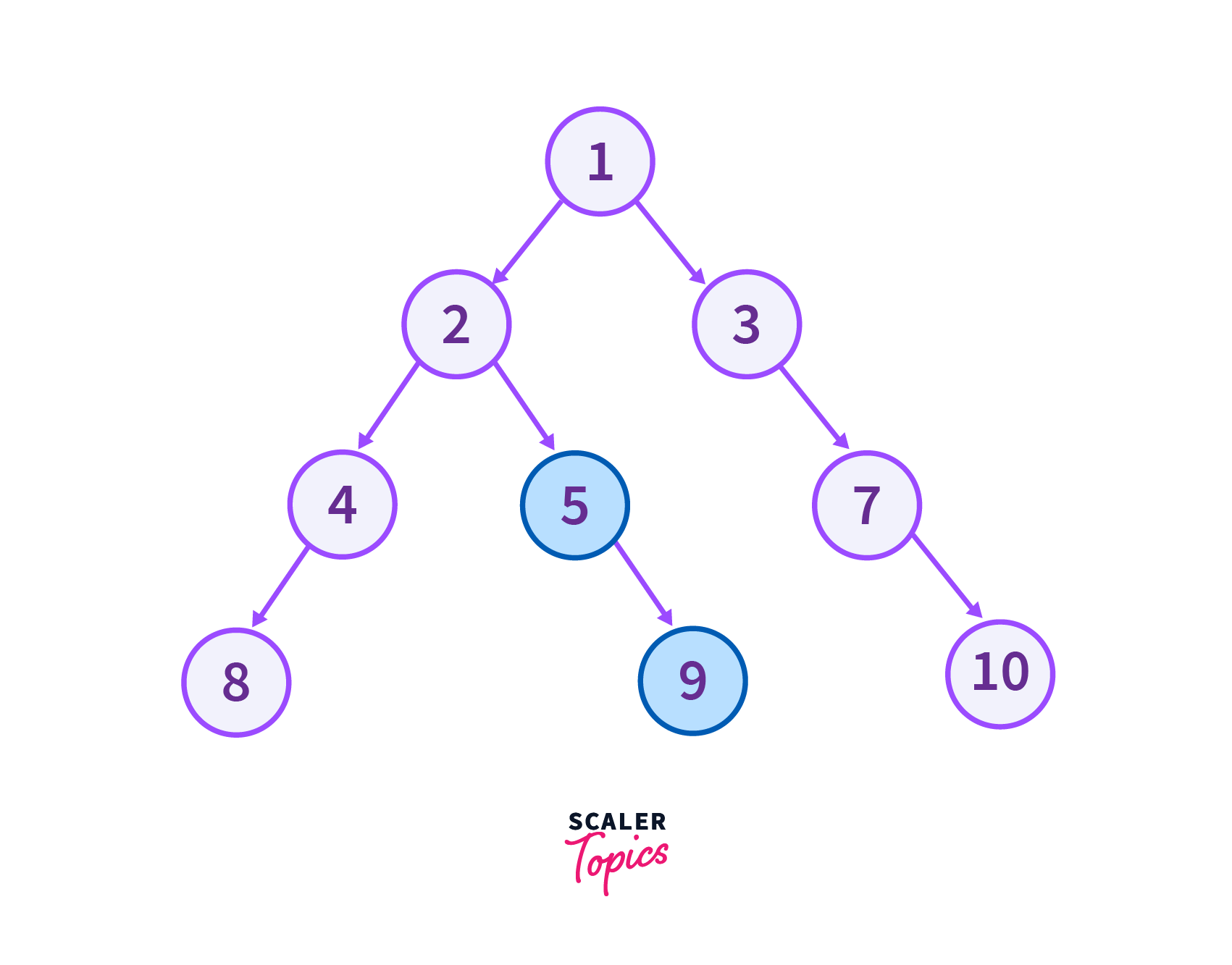
Output of the above program
Top View Nodes
8 4 2 1 3 7 10
Complexity Analysis for Top View of Binary Tree
Below is the Time and Space complexity analysis for the Top View of the Binary Tree.
Inorder to find the top view of the binary tree, we need to traverse all the nodes of the tree so it requires O(N) time also to store the node for the required comptation we use map in DFS and queue in BFS which takes an extra space of O(N) where N is the number of nodes in the binary tree.
Time Complexity: O(N)
Space Complexity: O(N)
where N is the total number of nodes in the given binary tree.
Conclusion
- In this article, we have learned how to find the
top viewof abinary tree. - We used two approaches to solve this problem which are as follows.
- Depth First Search Approach
- Breadth-First Search Approach.
- We have also analyzed the time complexity of the DFS and BFS based approach to find the Top View of the Binary Tree.
- And at the last, we have gone through some frequently asked questions related to this problem.
FAQs
Below are some of the Frequently Asked Questions related to the Top View of the Binary Tree.
Q How do you find the top view of a tree?
A. In order to get the top view of a tree we have to find the nodes which are visible from the top and we can get the required nodes by recursively storing the horizontal distance of every node from the root node starting from the left-most horizontal level to the rightmost horizontal level of the binary tree.
Q What is a treetop view?
A. Tree Top view is the set of nodes that are visible when a tree is viewed from the top.
Q Which node is found on the top of the binary tree?
A. The topmost node in a tree is called the root node. The root node is present at level 0 of the binary tree which is shown in the picture below.