Suffix arrays are very powerful data structures in terms of their applications in the field strings and string algorithms like pattern searching, string matching algorithms, the longest common prefix of two strings, counting the number of substrings, and in the field of biology some problems like DNA sequencing which uses suffix arrays to efficiently find the different longest matching subsequences in lexicographical order. Also, the most efficient construction of suffix arrays makes use of the old school technique used in sparse table, binary lifting i.e. using 2’s powers of strings. We shall learn the definition, implementation, and problem-solving using suffix arrays in this article.
Introduction to Suffix Arrays
- Suffix is the substring at the end of the string.
- Suffix array is the “lexicographically” sorted array of all suffixes.
In most of real-world problems, one may encounter a lot of instances of problem class that involve the use of suffix arrays for the efficient solution, for example, Geneticists are interested in the problem of DNA sequencing, Let’s understand the DNA sequencing problem.
The image below shows the structure of a DNA molecule.
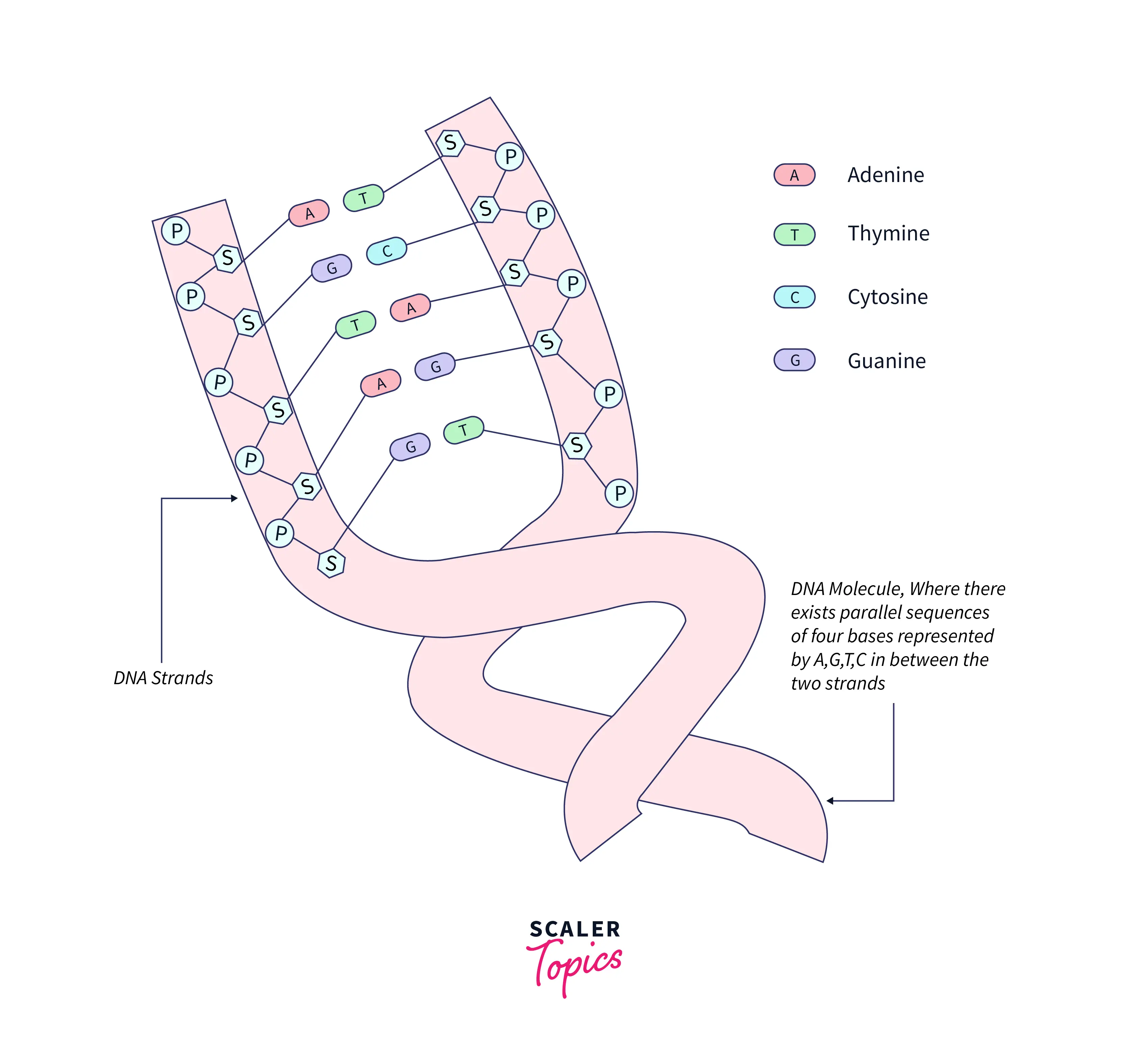
In the image above, the DNA molecule consists of two strands that wrap around each other and bear a resemblance to a twisted ladder where sides are made of phosphate and sugar molecules while they are connected by bases.
It can be seen that there are two parallel sequences of Bases where each sequence is associated with each strand represented by A,G,T, and C, and these sequences specify the exact genetic decree required to create an organism with its unique traits.
Geneticists are interested in the problem of finding the longest common base sequences in the two strands of a molecule given the two sequences of bases where each sequence is a string of length say N and consists of four letters a,g,t,c representing the nitrogenous bases.
For example, in two sequences as atgc and gctg, the longest common sequences are gc and tg, and we will learn to solve this problem and printing all such longest common sequences in lexicographical order using suffix arrays.
Let’s learn some basic terminology:
Suffix: It is a substring at the end of a string of characters, For our purpose, we shall consider only non-empty suffixes.
Below is an example of a substring
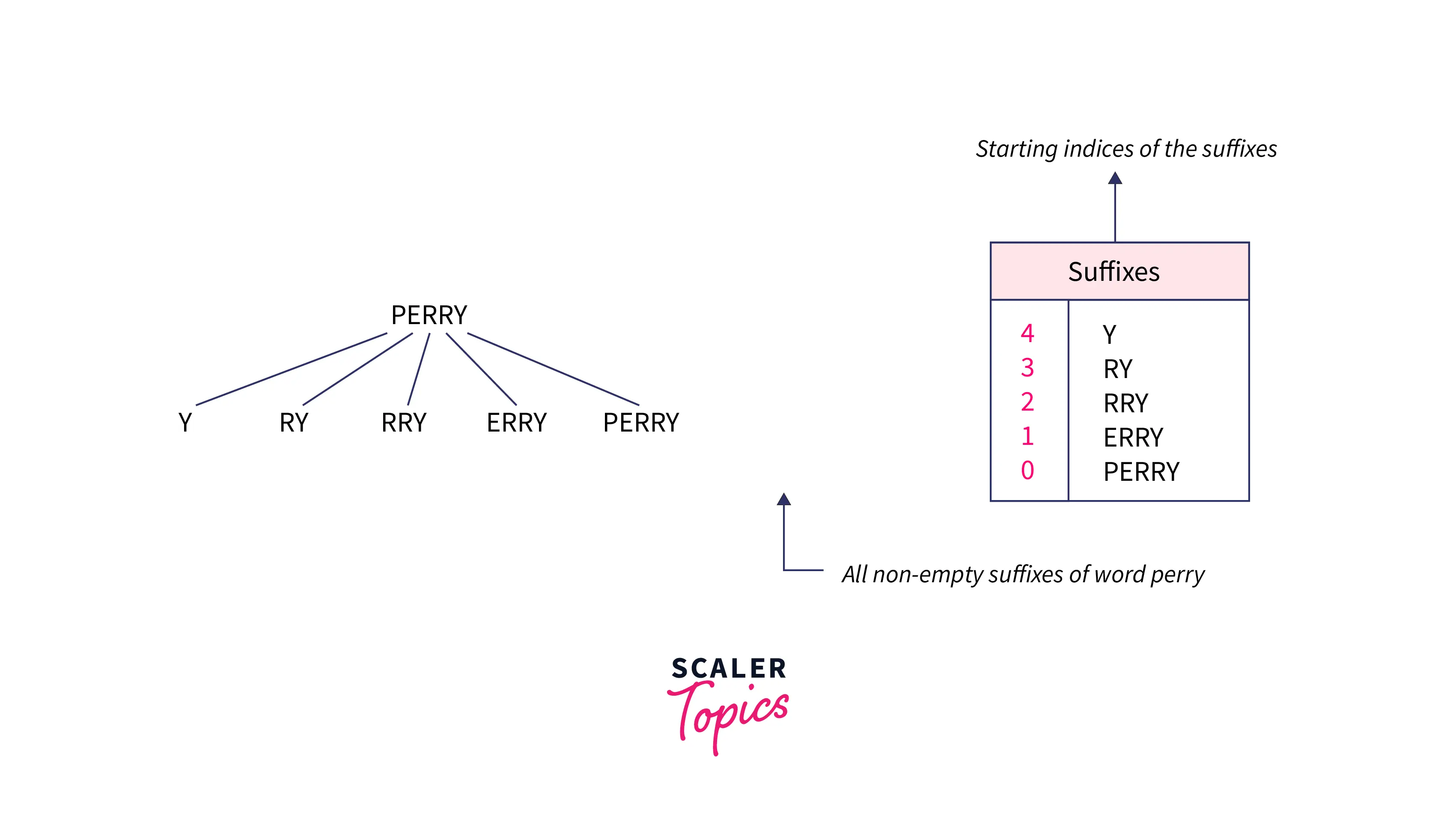
Suffix Array: It is an array of integers that represents the starting indices of the sorted array of all non-empty suffixes of a string where strings are sorted in lexicographical order.
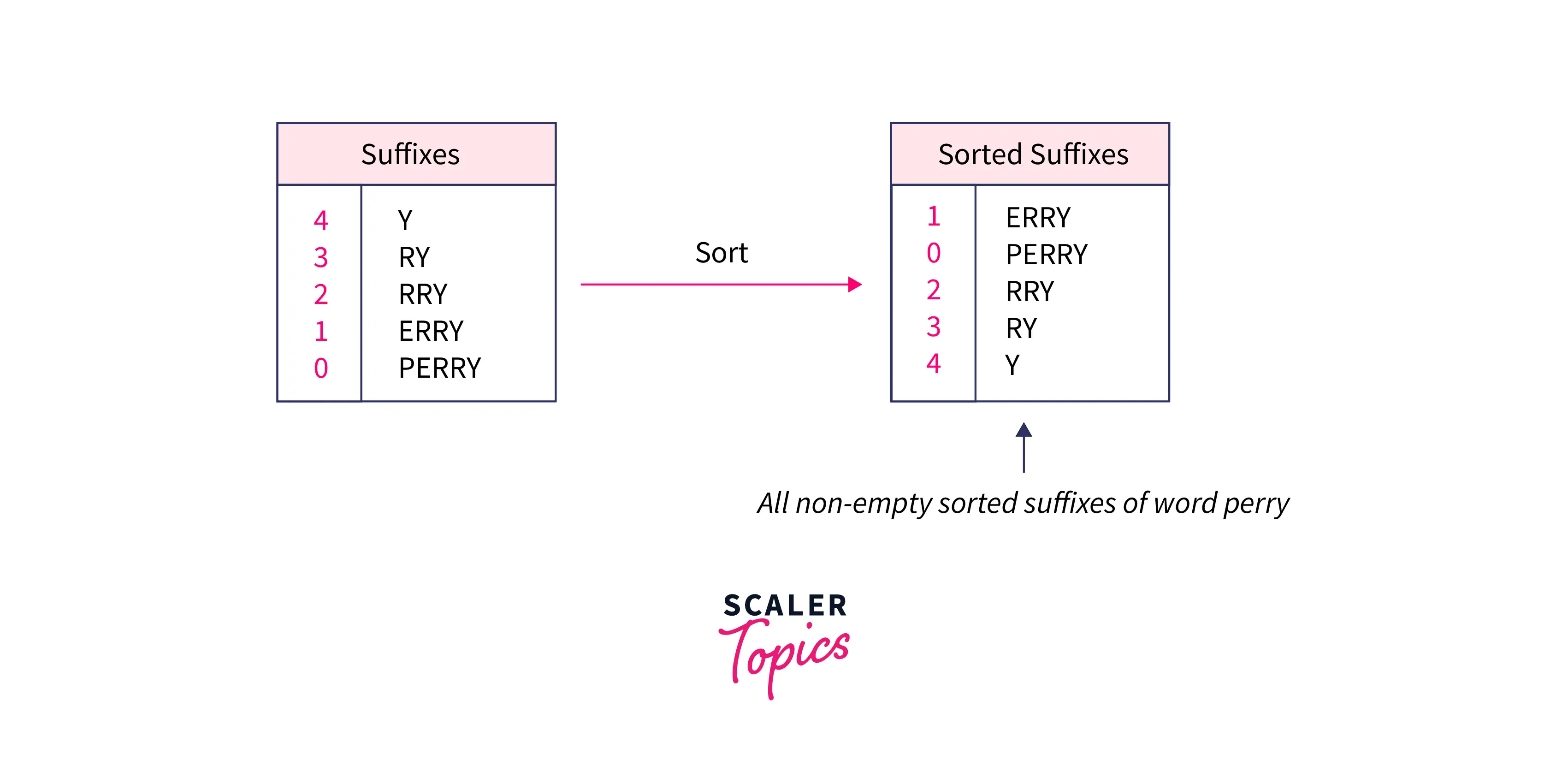
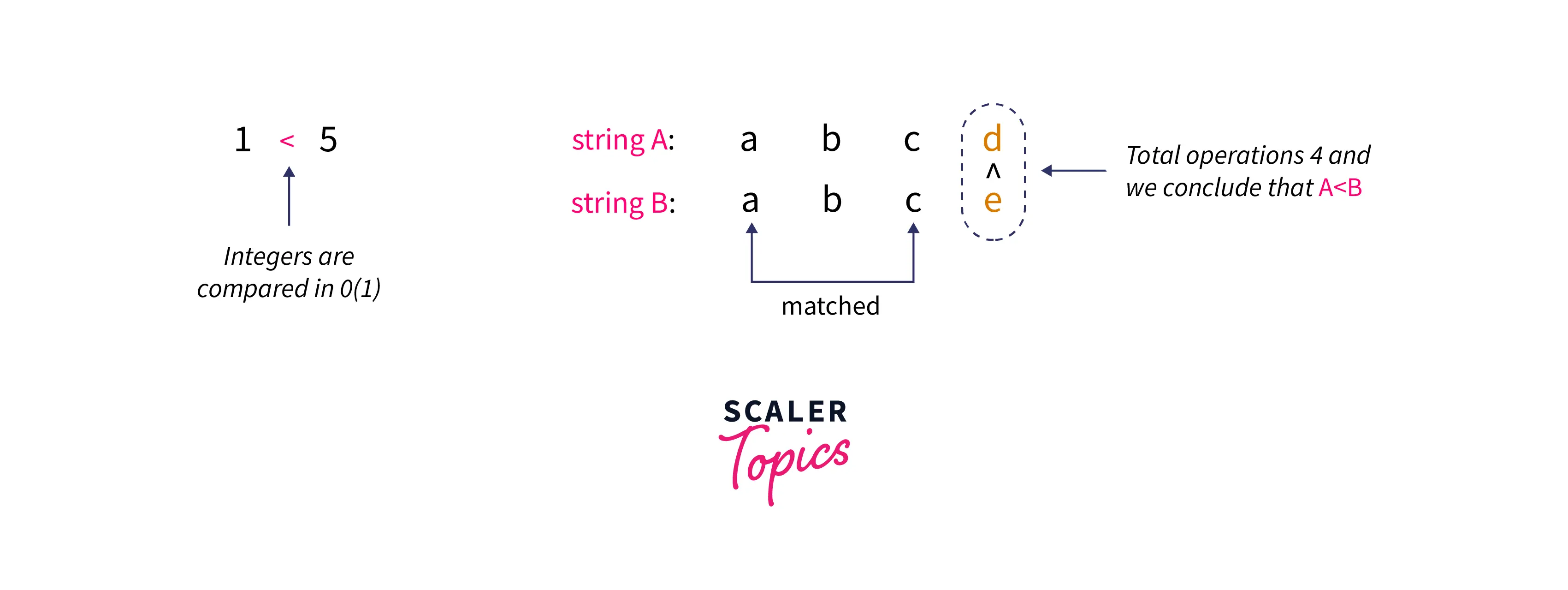
The suffix array stores the indices of the first character of the sorted suffixes of strings. Above suffixes are sorted lexicographically i.e. a string A is lexicographically lesser than string B if there exists an ith character in the prefix of A and B such that Ai < Bi. As shown below:
Therefore, the suffix array for the string PERRY will be (1,0,2,3,4) because we simply store the starting indices of the given suffix.
Now, after we know about suffix arrays, the follow-up questions are “How to build such data structure in the best possible ways?”, their time and space complexities.
Let’s answer these questions in the next section.
Construction of Suffix Arrays
- Naive implementation is inadequate for practical purposes.
- Binary search alongwith hashing brings the complexity of sorting comparator down to logN.
- Most efficient implementation of suffix arrays with complexity O(NlogN) uses type of dynamic programming approach.
Naive Implementation of Suffix Arrays
- We can use mergesort or quicksort alongwith a custom comparator to sort the suffix strings.
- Sorting of suffixes is to be done in lexicographical order.
- Sorting comparator of the naive implementation compares the suffix strings character by character.
Let’s think of implementing such data structure in the most simple way which can be called a suffix array, the first thought is to build a simple array of suffixes of the given string and sort them in lexicographical order, and then we simply retain the original indices of the suffixes as shown in the image below:
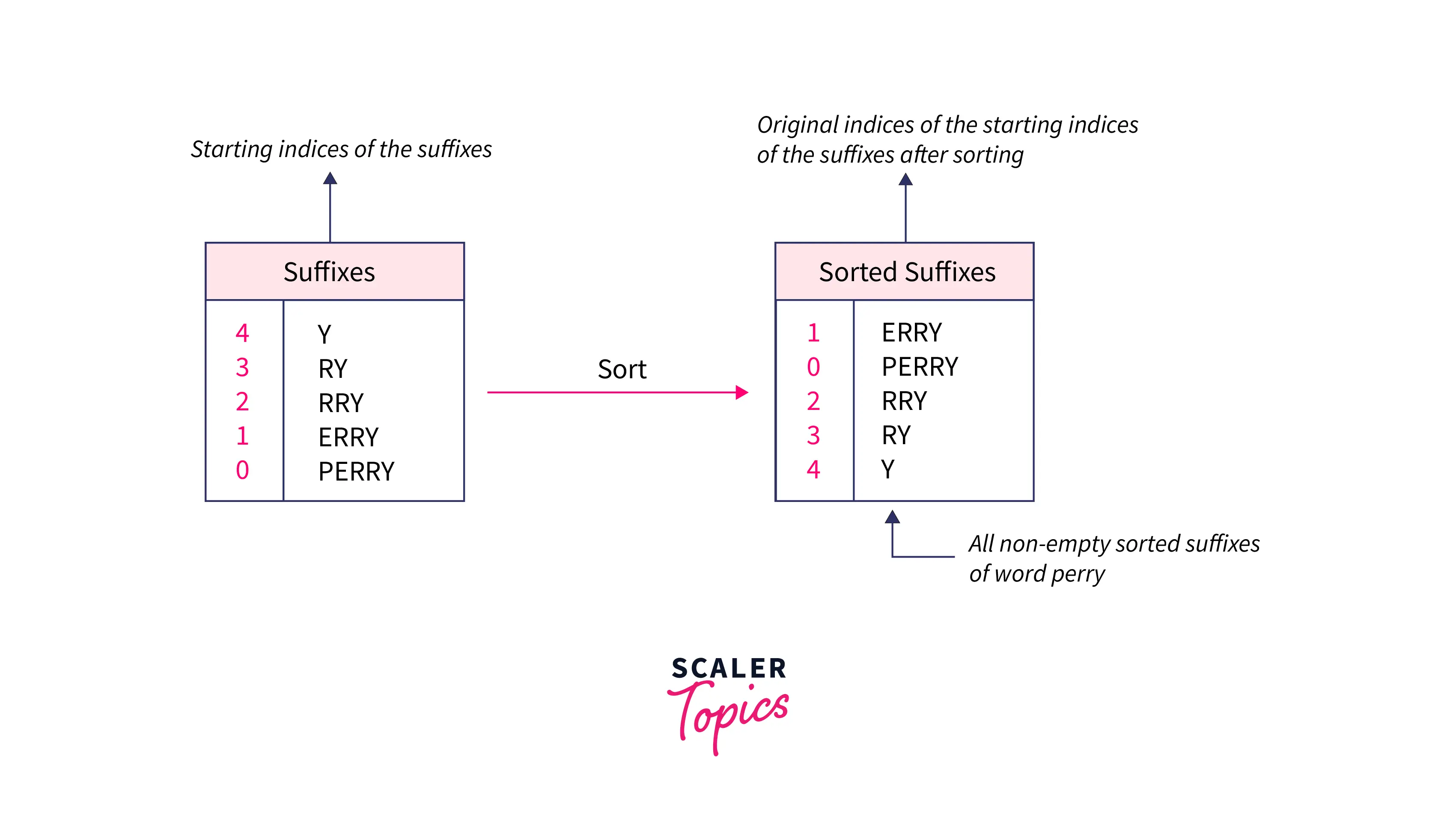
Think of sorting the array of strings in lexicographical order using say mergesort or quick sort i.e. very efficient “comparision” based algorithms. In sorting the strings using these algorithms we need to pass a custom comparator that compares the strings and places them in the array in the right lexicographical order.
Let’s implement the above strategy:
#include<bits/stdc++.h>
using namespace std;
//Structure to store information of a suffix
struct suffix{
int index;
char *suff;
};
//Custom comparator to sort the strings in lexicographical order
int comparator(struct suffix a, struct suffix b){
return strcmp(a.suff,b.suff) < 0 ? 1 : 0;
}
//Utility function to build the suffix array of the given text.
int *buildSuffixArray(char* text, int n){
// A structure to store suffixes and their indexes
struct suffix suffixes[n];
// Store suffixes and their indexes in an array of structures.
// The structure is needed to sort the suffixes alphabetically
// and maintain their old indexes while sorting
for (int i = 0; i < n; i++)
{
suffixes[i].index = i;
suffixes[i].suff = (text+i);
}
// Sort the suffixes using the comparison function
// defined above.
sort(suffixes, suffixes+n, comparator);
// Store indexes of all sorted suffixes in the suffix array
int *suffixArr = new int[n];
for (int i = 0; i < n; i++)
suffixArr[i] = suffixes[i].index;
// Return the suffix array
return suffixArr;
}
//A utility function to print an array of a given size
void printArray(int arr[], int n){
for(int i=0;i<n;i++)
cout << arr[i] <<" ";
cout <<"\n";
}
//Driver program
int main()
{
char text[] = "perry";
int n = strlen(text);
//Initialize an array pointer for suffixes.
int *suffixArray = buildSuffixArray(text,n);
//Print the builded suffix array
cout << "Suffix array for the " << text << " is as follows:" << "\n";
printArray(suffixArray,n);
return 0;
}
Let’s understand the above implementation of building the suffix array, struct suffix is a structure that represents a suffix string and it contains an index integer that represents the starting index of the suffix and an integer pointer suff which points to that starting character at that index.
comparator is the custom comparator used to sort the suffix strings in lexicographical order, it uses an inbuilt C++ function strcmp which compares the string character by character, however, it can be done using a for loop as well.
buildSuffixArray is the function used to build the suffix array of the given text, it does so by creating an array of the struct suffix defined above, of size same n as of the text say suffixes[n] where each struct object say suffixes[i] represents the starting index of the ith suffix i.e. suffixes[i].index and pointer to the ith character i.e. suffixes[i].suff.
When suffixes array is sorted with custom comparator comparator, it sorts the strings by comparing the suffix strings as pointers to the first characters of suffix strings are passed in the comparator, and in this way, the original indices(indices when we build them) of all the suffix strings can simply be retained by simply traversing the array suffixes and suffixes[i].index will gives the original index of the suffix string associated with this index.
Finally, we have the printArray function which simply prints the suffix array.
Let’s understand the time and space complexity of the above strategy:
Time Complexity
In sorting an array of strings using divide and conquer algorithms like mergesort or quicksort it takes O(NlogN) time complexity which in the comparison step of these algorithms, our program compares the suffix strings using the comparator passed which takes O(N) time complexity as explained below.
Comparator: The custom comparator compares the strings in lexicographical order and the comparator may take O(N) complexity in the worst case as one requires to traverse the two suffix strings while deciding the lexicographical order, unlike integers which takes O(1).
Therefore, the overall time complexity of building the data structure becomes O(N^2 logN). Similar arguments can be made with quicksort and it also has the order O(N^2 logN) time complexity.
Let’s discuss the space complexity of the above implementation:
Space Complexity
We get a linear time complexity O(N) as we are using an extra array of objects.
With the above complexity if we solve some practical problem of suffix arrays using the above implementation say for strings of order say 106106, it will take 106∗106∗log(106)106∗106∗log(106) i.e. roughly 10121012 iterations and in 1 sec the computer does 108108 iterations (i.e. For most of the online judges 1 sec is the time limit) and hence, it will take 1012/108=1041012/108=104 seconds which is roughly 2.5 hours and hence, the above strategy is inefficient for practical purposes.
Let’s build a more efficient approach for the Suffix arrays.
Binary Search with Hashing Approach for Suffix Arrays
- We can use mergesort or quicksort along with a custom comparator to sort the suffix strings.
- Sorting of suffixes is to be done in lexicographical order.
- There is always a matching prefix for any two suffix strings not necessarily non-empty.
- Monotonic pattern exists because of the matching prefixes.
- Sorting comparator makes use of binary search along with hashing to bring its complexity down to O(logN).
In the last approach, the problem we faced is with the comparator as it takes O(N) complexity for comparing two strings as it compares each and every character of two strings.
While the comparator compares the two strings, it can be observed that there exists a matching prefix(not-necessarily non-empty) in two subject strings and we can see that there exists monotonicity here i.e. if we define a predicate function say isMatching(a,b) which returns TRUE if characters a and b of the subject strings matches else it returns FALSE, same is depicted below:
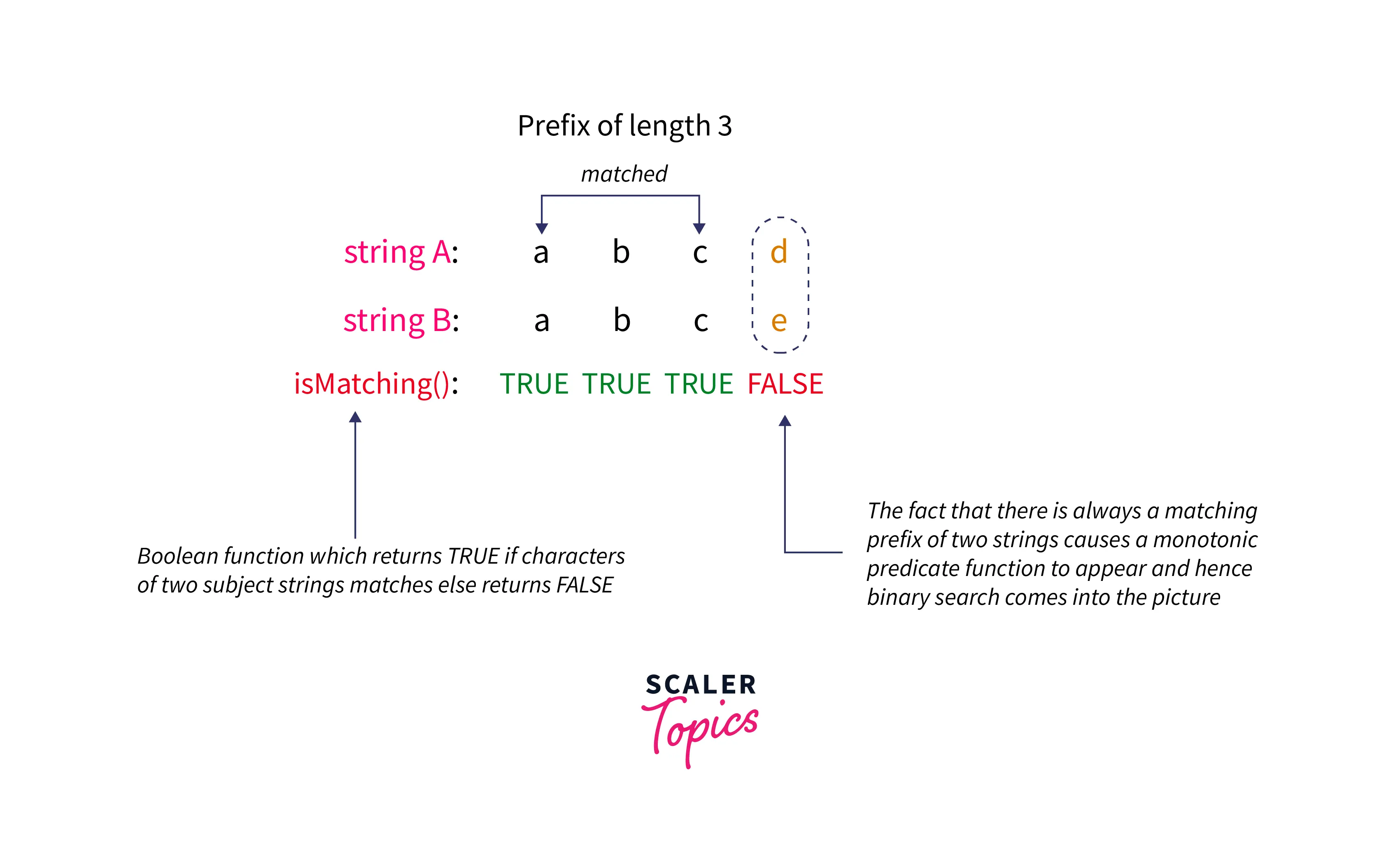
But we are interested in the first character of the two subject strings where the characters mismatch and this character decides which one of the strings is lexicographically smaller, While isMatching(a,b) does not ensures that if say ith character matches then all jth characters such that j < i and j >= 0 matches or not i.e. the function isMatching(a,b) is not a monotonic function as shown below:
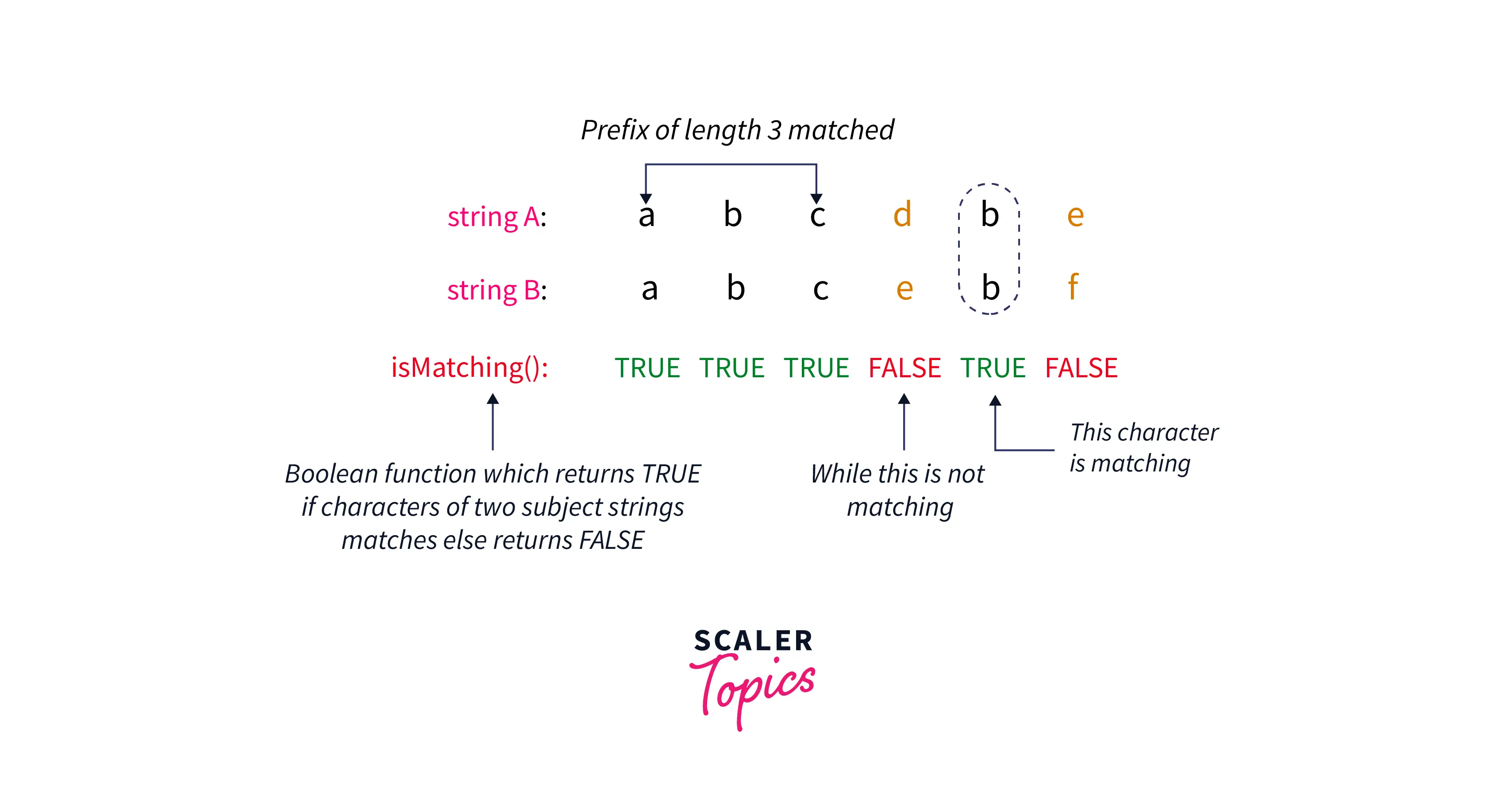
Since, isMatching(a,b) is not a monotonic function, binary search cannot be used to get the first non-matching character which decides the lexicographical order of the subject strings.
To solve this problem, we shall create a hash table such that hash(i,j) defines a unique hash value for this particular arrangement of characters starting at i and ending at j such that whenever the same arrangement of character (substring) appear the hash function returns this specific hash value.
We compute this hash function on each prefix of the strings i.e. compute hash(0,i) for all 0 <= i < N for both strings where N is the minimum of the lengths two subject strings.
hash function is to be defined in such a way that if a prefix of length l of two subject strings matches and the lth character does not match then the hash of the two strings upto the l-1th character i.e. hash(0,l-1) must be same and after that i.e. starting right from lth character the hash of the prefixes two strings i.e. hash(0,x),x >= l must not match for any index no matter how many matching charaters appear, in other words, the hash function must be monotonic function.
Once this happens, the hash(i,j) is completely monotonic function and the dilemma with isMatching(a,b) is solved, Now, we do not need to compare characters of two strings rather we compare the hashes of the two strings upto a certain length of the string because hash function is monotonic and hence isMatching is modified to compare the hashes of the prefixes of the subject strings rather than characters as shown in the image below:
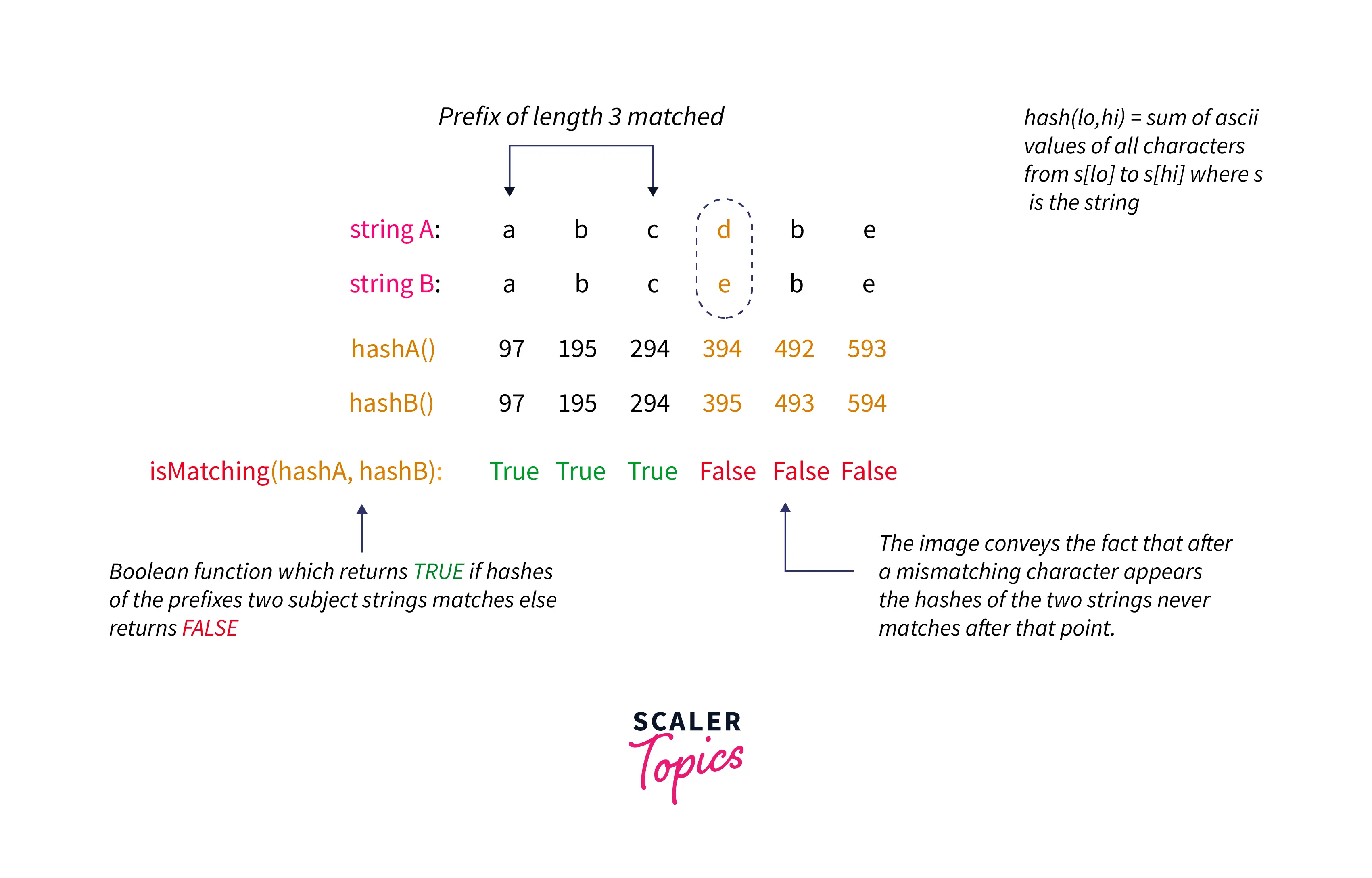
Now, we have turned the isMatching function into a complete monotonic function and our target is to obtain the right lexicographical order by comparing two strings and hence, we use binary search on answer strategy to reach to our first non-matching character of the two subject strings as we have got monotonic isMatching function.
The next questions to be answered are how to define hash function that gives minimum collision, how to implement the above strategy to get the complexity of the comparator down, let’s delve into it.
It is obvious that the main requirement of the hash function is that it must depend on the particular arrangement of the prefixes for example, the hash of the strings “abc” must not match with the hash of the string “acb” although the characters are same in both the strings.
We define the hash as hash(i) to be a monotonic function of the previous hash i.e. hash(i-1) and the current ith character of the string.
It can be the sum of the previous hash and the ascii value of the current character but another constant factor particularly a large prime(at least larger than all characters that may appear) number is multiplied with hash(i-1) before adding it so as to avoid collision.
Hence, we define the hash function for some string s as:
hash(i)=hash(i−1)∗Delta+s[i],whereDelta=137
The next part is the implementation of the strategy that we obtain by observing the above monotonic patterns, let’s redefine the sorting comparator.
We can now instead of linear scan , first precompute the hashes of all prefixes and then perform binary search on the hashes i.e. we want to find the last character where the hases match or in other words largest prefix where hashes match or prefixes match and the first mismatching character will decide the right lexicographical order of the suffix strings.
The rest of the implementation stays the same as the previous naive implementation but the comparator will behave differently.
Let’s see the implementation of the above strategy in C++ programming language:
#include<bits/stdc++.h>
using namespace std;
//Uppper bound for the suffix array
const int
MAXN = 1 << 21;
//Constant prime used to avoid collision
const int Delta = 137;
//Declare the size of the string
int N;
//String pointer
char * text;
//Declare the suffix array and hashtable
int suffixArray[MAXN];
unsigned long long hashTable[MAXN], hashPow[MAXN];
//Returns the hash value in O(1)
#define getHash(lo, size) (hashTable[lo] - hashTable[(lo) + (size)] * hashPow[size])
//Comparator used to sort the suffixex using binary search + hashing
inline bool sufCmp(int i, int j)
{
int lo = 1, hi = min(N - i, N - j);
while (lo <= hi)
{
int mid = (lo + hi) >> 1;
if (getHash(i, mid) == getHash(j, mid))
lo = mid + 1;
else
hi = mid - 1;
}
return text[i + hi] <text[j + hi];
}
//Function to build suffix array over the string text
void buildSuffixArray()
{
N = strlen(text);
//Precompute the hashPow array
hashPow[0] = 1;
for (int i = 1; i <= N; ++i)
hashPow[i] = hashPow[i - 1] * Delta;
//Compute the hash table
hashTable[N] = 0;
for (int i = N - 1; i >= 0; --i)
hashTable[i] = hashTable[i + 1] * Delta + text[i], suffixArray[i] = i;
//Run the stable sort
stable_sort(suffixArray, suffixArray + N, sufCmp);
}
int main(){
//Input string
text = "perry";
//Call the function which builds the suffix array
buildSuffixArray();
//Print the builded suffix array
for(int i=0;i<N;i++)
cout << suffixArray[i] << " ";
}
Time Complexity
The time complexity of sorting stays the same as in the naive algorithms i.e. we can use mergesort or quicksort which takes O(NlogN) while the complexity of the comparator is changed from O(N) to O(logN) because we are using binary search with hashes and this will bring the implementation of the comparator down to O(logN) because there will be at most ceil(logN) comparisons before we get our first mismatching character, Hence, the overall time complexity of the approach is O(Nlog^2N).
Space Complexity
We get a linear time complexity O(N) as we are using an extra array of objects and array and O(N) for storing the hashes, hence the overall space complexity is O(N).
Efficient Implementation of Suffix Arrays
- Sorting of suffixes is to be done in lexicographical order.
- Sorting the cyclic substrings instead of actual suffixes will do the job.
- Idea similar to binary lifting, sparase table is used i.e. something realted to 2’s power.
- Rank of the cyclic shift of a substring will decide the suffix array.
- Suffix array is a permutation of all integers 0 to N-1.
While implementing a naive strategy it is explicit that sorting is always required for building suffix arrays with any method possible (as it is clear from the definition of suffix array), but the inefficiency arises due to the comparator used to sort the suffix strings in lexicographical order, it multiplies the sorting complexity O(NlogN) by a factor of N to make it O(N2logN), Hence, we need to modify the implementation such that the complexity due to the comparator is reduced. Let’s see how we can do this:
As we know suffix arrays are just starting indices of non-empty sorted suffix strings, hence our target is to store the starting indices of the non-empty sorted suffix strings.
The idea that we are going to use is that the strings in the suffix array are lexicographically sorted, using this information we can give rank/class to the different suffixes, and based on the rank of smaller suffix strings we can also manipulate the ranks of larger suffix strings as larger suffix strings are just the concatenation of some of the smaller suffix strings.
The idea is shown in the image below:
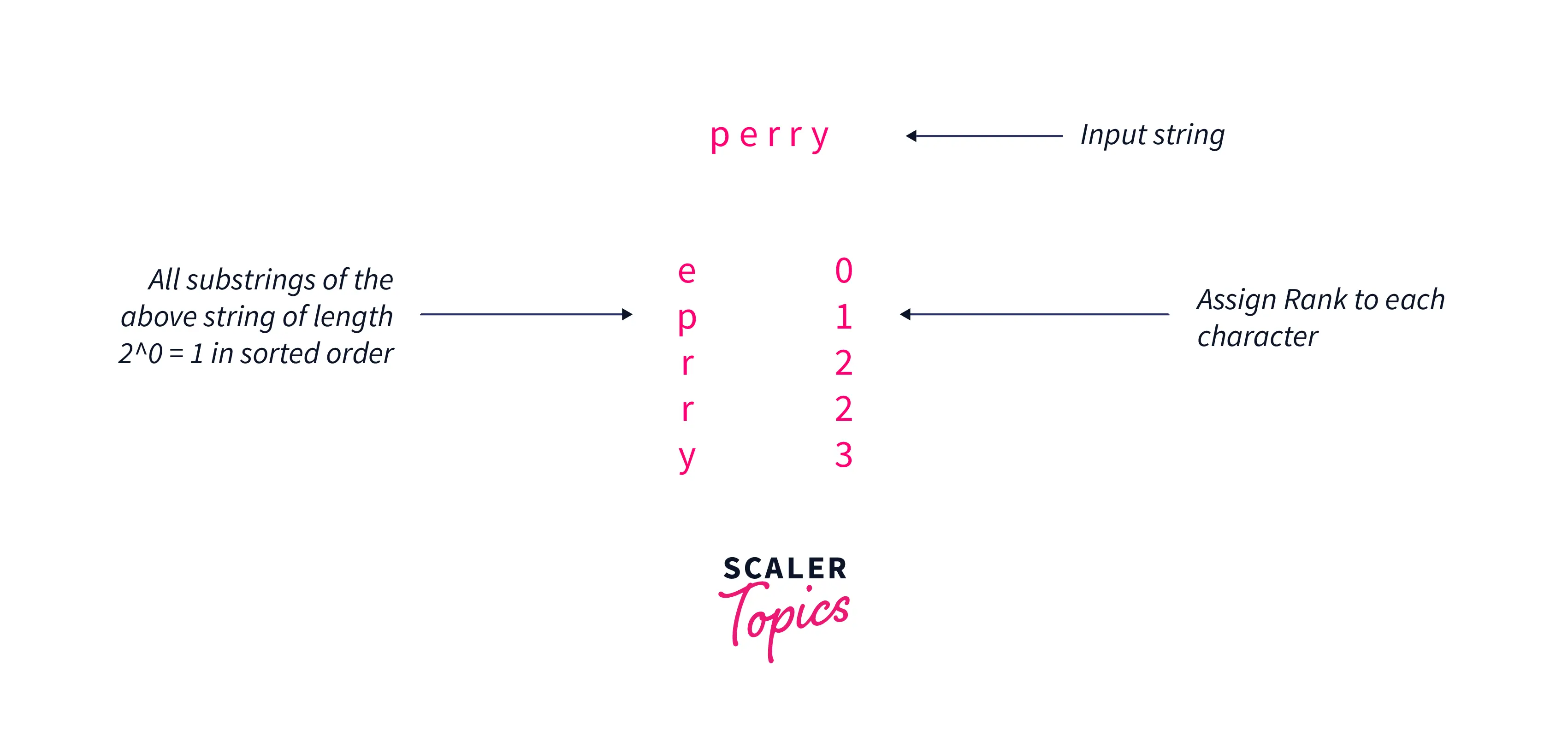
Here, we assigned a rank to each substring of size 2^0 = 1 according to the ASCII values of the characters, Using the rank of the above characters we can find the rank/class of the strings of length 2^1 = 2 as shown below:
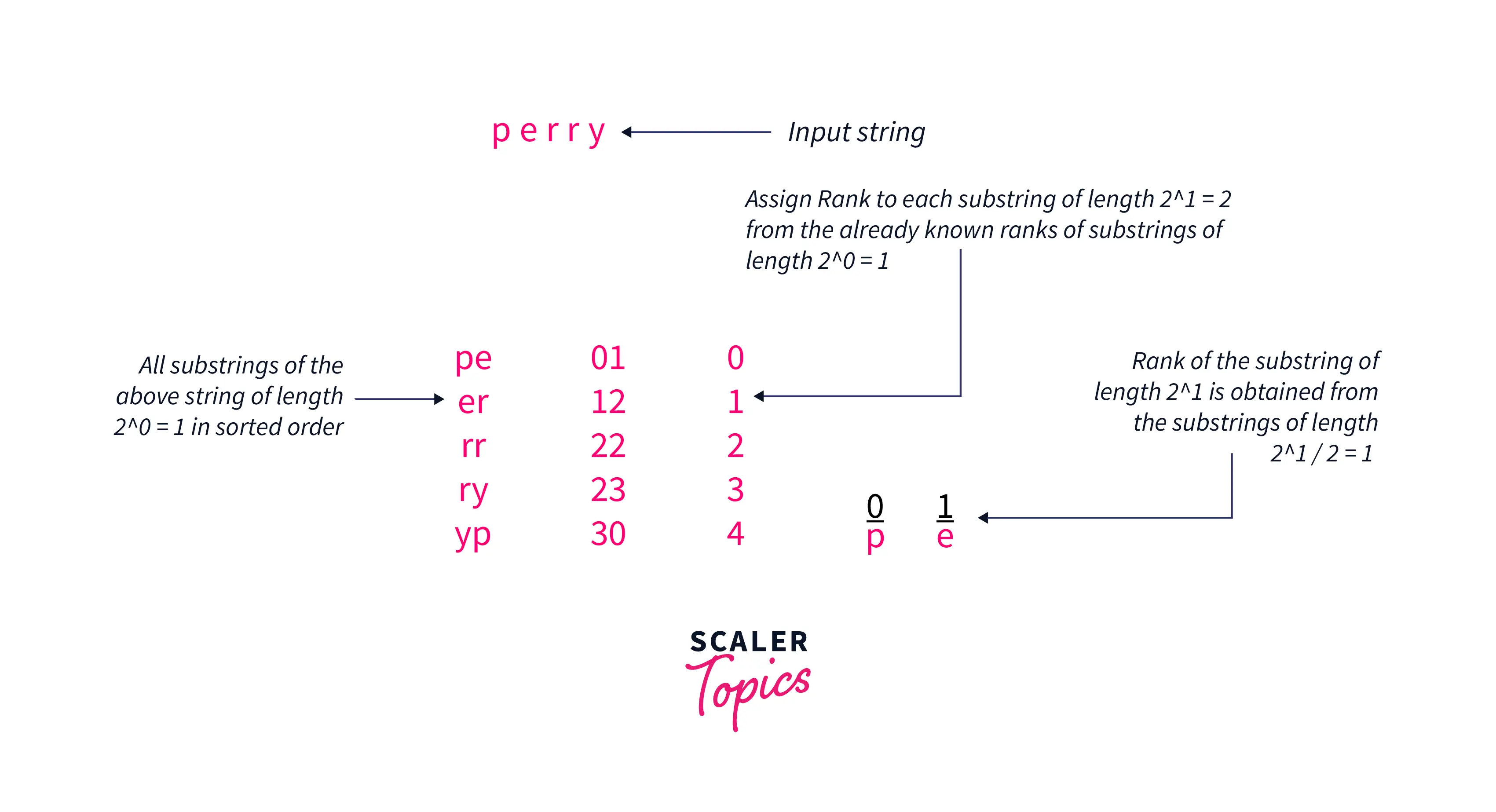
Here, we obtained the ranks of the substrings of length 2^1 = 2 from the substrings of length 2^1 / 2 = 1. Similarly, the ranks of substrings of length 2^2 = 4 can be obtained from the ranks of substrings of length 2^1 = 2.
Note: In general, the rank of a substring of length 2^k can be obtained from the ranks of the substrings of length 2k−12k−1.
Let’s see how this idea can help us to build the suffix arrays in a better way.
Until now, we can conclude that if the suffixes of a string have a length as 2’s power then it is easy to compute their ranks, and based on their ranks (as rank decides the place in the suffix it will exist).
But the question to be answered is how these ranks may help us to obtain the suffix array.
Let’s try to solve the main problem using the above observations and conclusions.
In this technique, we sort the cyclic shifts of the string rather than sorting the suffixes of the string literally, and by doing so we can easily get the sorted suffixes.
First of all, we need to make all the sorted suffixes to have the length as some power of 2 without changing the lexicographical order.
To do this we append a character at the end of each suffix that is smaller than all the characters that may ever appear in the string and then add the cyclic shift of the parent string to make each suffix have a length as the power of 2.
Let’s understand the above scenario with an example as shown below:
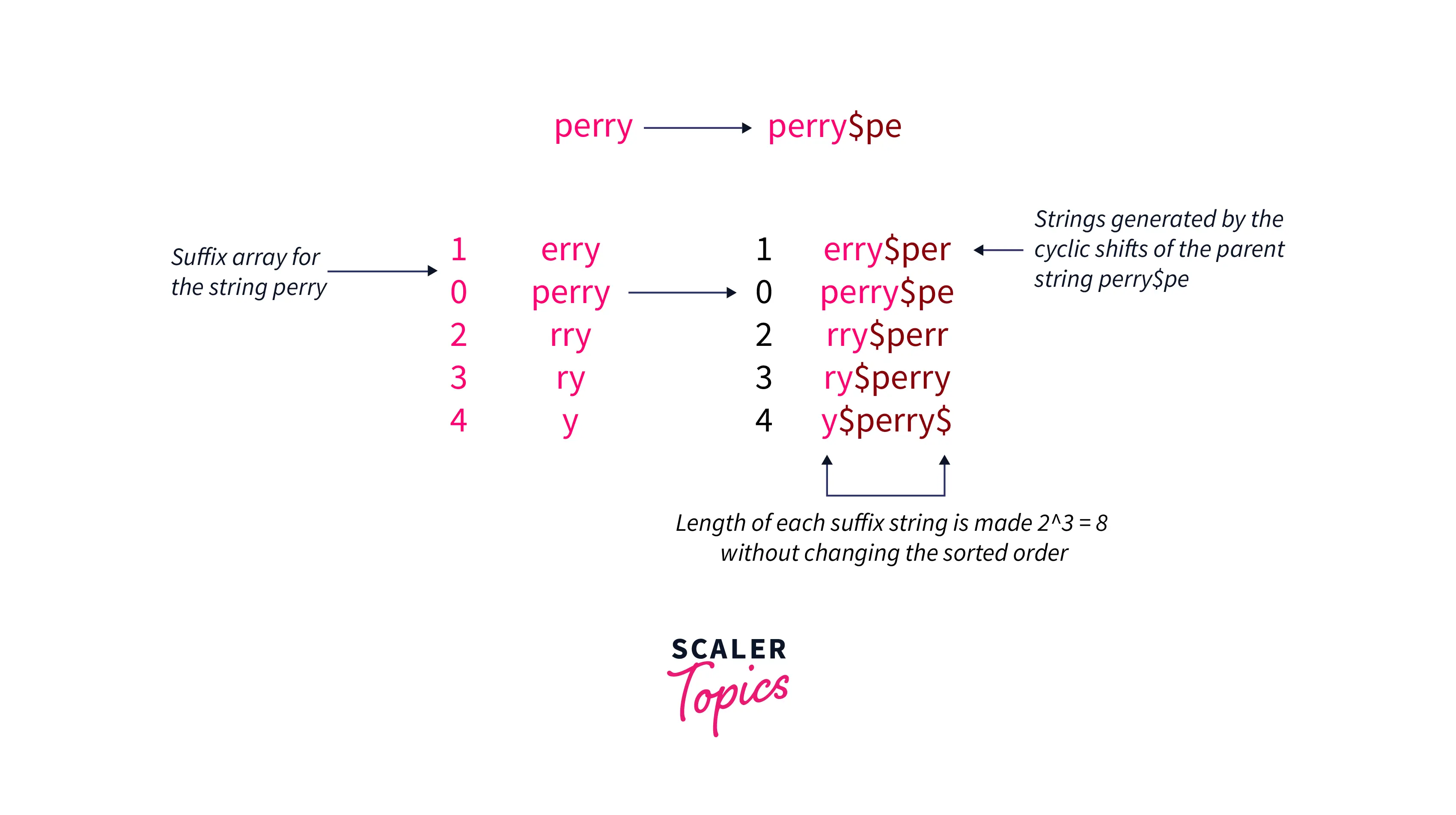
We appended a character $ which is smaller than all the characters that may ever-present in the string, this is because while we add cyclic shifts of the string to each suffix to make its length as 2^k, it will not affect the lexicographical order as shown below:

Now, we shall sort these cyclic shifts of the suffix strings and any cyclic shift can be represented by s[i…j] when i > j it is splitted as s[i..j] = s[i..n-1] + s[0..j].
In this algorithm, we shall sort n cyclic shifts of strings of lengths 2^k, now what should be the range of k, it is obvious that we shall sort all strings starting from each index i.e. i = 0 to i = n-1.
In other words it can be represented as:
Sort s[i, i + 2^k – 1] in cycle where i = 0 to i = n-1
Where k = 0 to k = ceil(logN)
We basically perform k = ceil(logN) phases and in each phase, we generate two arrays p which is a permutation array of length n where p[i] is the index of the ith substring starting at i and has length 2^k.
Also, we shall keep an array c which is the class/rank array where c[i] represents the class/rank to which this substring(ith-substring starting at i with length 2^k) belongs.
Hence, we start from k = 0 and grab all substrings of length 2^k = 2^0 = 1 and sort them and we build array p and array c as follows:
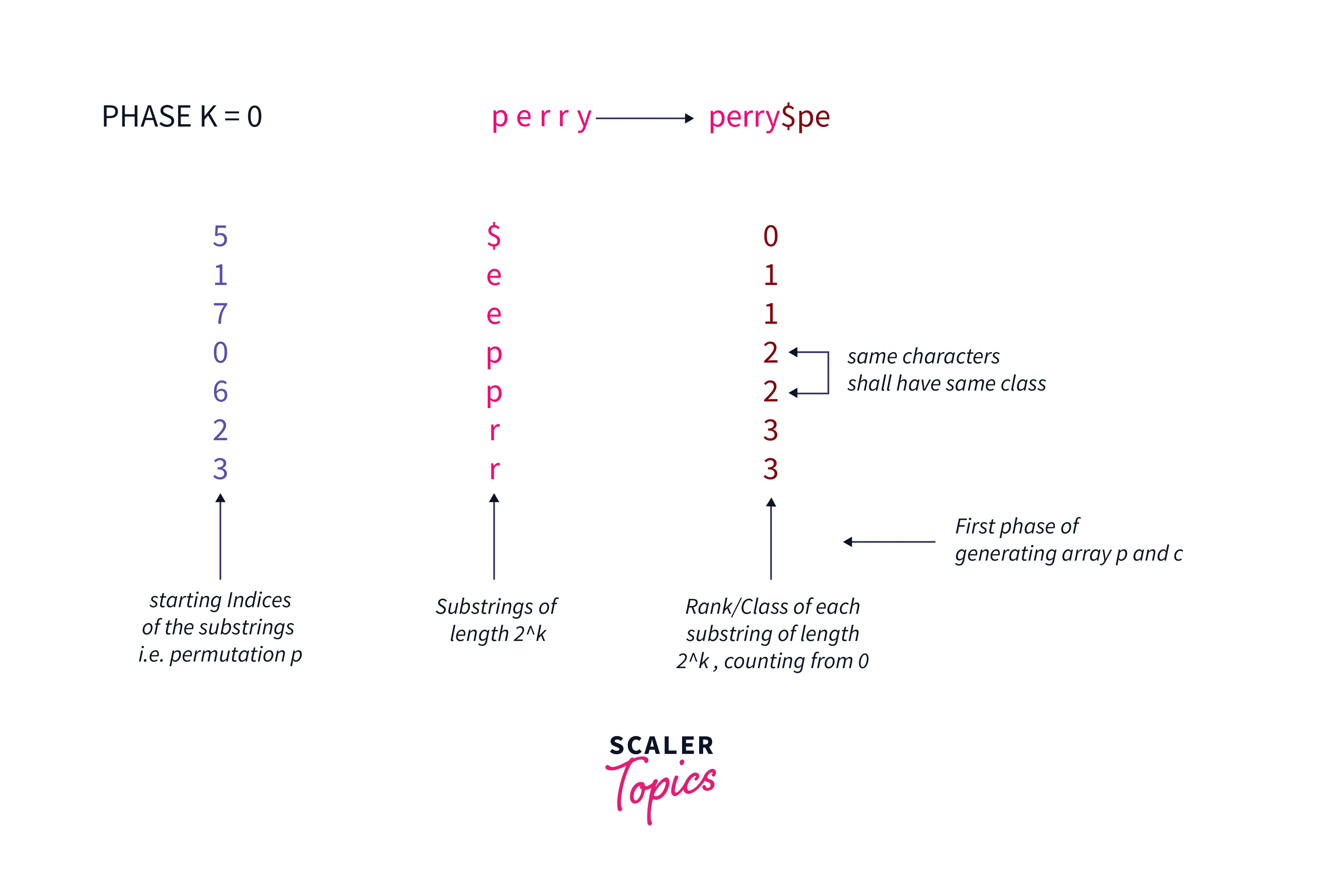
The above image shows the first phase of generating the array p and c and in the next section, we shall learn how we build the suffix array in k = ceil(logN) phases.
Now, after we have our first phase completed, other phases can be generated i.e. the permutation and class arrays p and c respectively can be generated from it.
For phase transition from K to K+1:
To generate the equivalence class for substring starting at i of length 2^k, Since it consists of two substrings of lengths 2^k-1 starting at i and i + 2^k-1 it simply requires the pair (c[i],c[i+2^k-1]) i.e. equivalence classes of the previous phase as shown below.
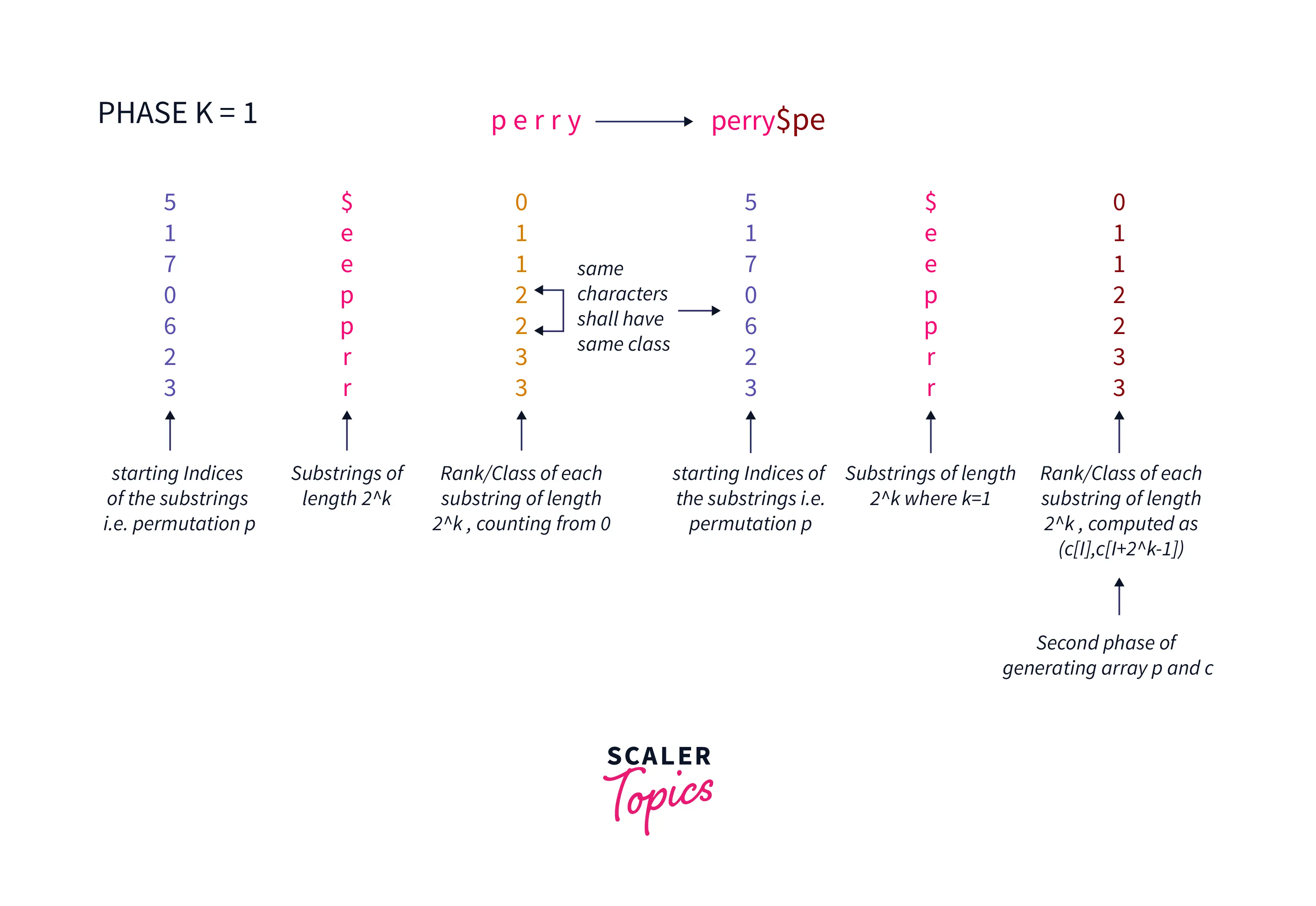
It is explained before that how ranks/classes of substrings of length 2^k are generated from ranks/classes of substrings of length 2^k-1.
Hence, according to these pairs (c[i],c[i+2^k-1]), the substrings are compared in O(1) to get a sorted array of substrings according to the rank/class and it is obvious that this comparison will arrange the substrings in lexicographical order and hence we obtain the array p.
Normal sorting (mergesort or quicksort) will take O(NlogN) and hence this will take O(Nlog^2N) which can be improved by using the fact that all ranks/classes are within the range [0, N] and also the fact that the class c was already sorted for the previous phase i.e. first elements of the pairs are already sorted.
Thus we need to sort the elements just by the second pair, in order to do that we use a trick and here we see the power of this data structure, to sort the pairs by second elements we need to subtract 2^k-1 from the indices given in the permutation p which was computed for the previous phase.
In order to understand this consider that if the smallest substring of length 2^k-1 starts at index i, then to bring this substring to the right side of the next phase i.e. the substring of length 2^k with the smallest second half must start at i – 2^k-1.
By using these substractions we can sort the pairs by second elements and to sort by the first element, we can use counting sort.
Now, we have generated the permutation p for this phase K from the last phase K-1, the next thing is to generate the class c for this phase and it can be generated by simply iterating over pairs that have been generated and comparing them.
After, we complete ceil(logN) phases we have our p array which is a sorted array of substring indices such that p[i] gives the index of the ith substring of length 2^k (here k = ceil(logN)) and it contains the same order of indices as the order of sorted suffixes.
Let’s see the implementation of the above idea in the C++ programming language:
#include<bits/stdc++.h>
using namespace std;
//Function to generate the suffix array p
vector<int> sort_cyclic_shifts(string const&s){
//size of the string
int n = s.size();
//will be used to generate frequency array
const int alphabet = 256;
vector<int>p(n),c(n), count(max(alphabet,n),0);
//count the frequency of each character
for(int i=0;i<n;i++)
count[s[i]]++;
//Preprocess the prefix sum
for(int i=1;i<alphabet;i++)
count[i] += count[i-1];
//Process the permutation array p for the first phase
for (int i = 0; i < n; i++)
p[--count[s[i]]] = i;
//Process the classes array
c[p[0]] = 0;
int rank = 1;
for(int i=1;i<n;i++){
// same characters get the same rank/class
if(s[p[i]] != s[p[i-1]])
rank++;
c[p[i]] = rank-1;
}
//After phase first , we use temporary arrays to build p,c for this phase from previous p and c.
vector<int>pn(n),cn(n);
//Now we process these arrays for each of the k phases
for(int k=0; (1 << k) < n; k++){
//used to get the array p for this phase
for(int i=0; i <n; i++){
pn[i] = p[i] - (1 << k);
if(pn[i] < 0)
pn[i] += n;
}
//Initialize the array cn with 0
fill(count.begin(), count.begin() + rank, 0);
//repeat the same procedure
for (int i = 0; i < n; i++)
count[c[pn[i]]]++;
for (int i = 1; i < rank; i++)
count[i] += count[i-1];
for (int i = n-1; i >= 0; i--)
p[--count[c[pn[i]]]] = pn[i];
cn[p[0]] = 0;
//Reinitialize Rank
rank = 1;
//Compute classes for this phase from the pairs evaluated
for (int i = 1; i < n; i++) {
pair<int, int> cur = {c[p[i]], c[(p[i] + (1 << k)) % n]};
pair<int, int> prev = {c[p[i-1]], c[(p[i-1] + (1 << k)) % n]};
if (cur != prev)
++rank;
cn[p[i]] = rank - 1;
}
//We swap the c for this phase into the previous c
c.swap(cn);
}
//Return the suffix array
return p;
}
//Function to construct the suffix array
vector<int>construct_suffix_array(string s){
// add special character
s += "$";
//Call the function which performs the relevant phases
vector<int>suffix_array = sort_cyclic_shifts(s);
//Erase the first element because it is for the $ sign
suffix_array.erase(suffix_array.begin());
return suffix_array;
}
//Driver program
int main(){
//Input string
string text = "perry";
//Call the construct suffix array function
vector<int>sorted_shifts = construct_suffix_array(text);
//Print the suffix array
for(auto it: sorted_shifts){
cout << it << " ";
}
}
Let’s discuss the time complexity of the above implementation
Time Complexity
We are doing ceil(logN) iterations for building the arrays p and c, where each iteration is also regarded as phase, and in each phase we sort using counting sort which takes O(N) complexity and hence, the overall complexity becomes O(NlogN). The actual power of the data structure is seen when we sort the second elements of the pairs just by subtraction.
Space Complexity
We are processing arrays p, c and other temporary arrays in between the building process and all of them gives a lines time complexity O(N) and hence the overall space complexity is also O(N).
Applications of Suffix Arrays
- Solving the old DNA sequencing problem using suffix arrays.
- Finding a substring in a string using suffix arrays.
- How to compare two strings of same length in O(1) using suffix arrays.
1) DNA Sequencing Problem
This problem as formulated at the beginning of the article requires all longest common sequences in lexicographical order of the two given base sequences provided in the form of strings containing letters a,c,t,g only.
The problem can be easily solved by first concatinating the given two strings of bases and then building suffix arrays and LCP array in O(NlogN) where LCP array is the longest common prefix array and is an auxiliary data structure to the suffix array, It basically stores the lengths of the longest common prefixes between all pairs of consecutive suffixes in a sorted suffix array.
Now, we find those positions in the LCP array where two consecutive suffixes are from two different strings (given initially), Here we take the maximum of these prefixes i.e. LCP, Now we generate string from this position with already computed maximum length value, from these strings print all distinct strings it can be done using a set.
This takes O(NlogN) overall time complexity while we can solve the same problem using O(N^2) LCS dynamic programming approach but that would be inefficient in case of high order input of order say 10^6.
2) Finding a Substring in a String
In some of the programming contest problems we are given the task to search, some patterns say pat in some text for some q online queries say, by online means the result of the ith query will determine the answer to the i+1th query. To do this we first process the suffix array p using the efficient strategy in O(|text|log(|text|)) and observe that the array p contains all the first indices of all suffixes in sorted order of suffixes and the string pattern pat must be a prefix of some suffix of the text and hence there is monotonicity and we can use binary search for finding out the given pattern pat in the array p.
Comparision for the pattern pat for each suffix can be made in O(|pat|) time complexity to give an overall complexity of O(|text|.log|text|.|pat|.log|text|).
However, it can be reduced to O(|text|.log|text|.log|text|) by optimizing the comparing pat process using hashing.
3) Comparing Two Substrings of a String
In this problem category, we are required to compare the two substrings of a string in O(1), by comparing means finding out the right lexicographical order between them. While building the suffix arrays we used equivalence classes or ranks to determine the right order of the strings i.e. the one with a lesser magnitude of class comes first in lexicographical order.
Since we processed the equivalence classes of all substrings which has length as the power of 2, hence to compare two strings that are the power of 2 lengths, it is enough to compare the equivalence classes of the respective strings and for that, we need to store the results of equivalent classes for all intermediate steps and in this ways, we would be able to compare two substrings in O(1).
In the case of substrings having an arbitrary length (i.e. may or may not be a power of 2) and here comes the same magic of binary jumping or sparse table concept, remember we split any integer into the powers of 2 like for 7 = 2^2 + 2^1 + 2^0, Let’s understand how this will help us to compare two substrings of length l starting at index i and j.
We start with the largest number less than equal to l starting at i and j which is a power of 2 i.e. 2^k <= l and we compare the equivalence classes of these two numbers(remember we already have stored equivalence classes) i.e. the comparison of substrings is replaced by the comparison of the overlapping classes of the substrings, if they do not match then we already get the right lexicographical order i.e. the substring with smaller equivalence class will come first. Otherwise, we now compare the blocks ending in positions i + l – 1 and j + l – 1 (notice they will be overlapping with the previous block), now we compare c[i + l – 2^k] and c[j + l – 2^k] and this will give us the right order.Remember same we do with the sparse table when we evaluate some idempotent functions. It is obvious that the above comparison works in O(1) as we are just using two comparisons.
Conclusion
- We conclude that suffix arrays are used in many problems related to strings like pattern searching, DNA sequencing, and many more.
- The power of suffix arrays lies in the fact that they bring the complexity of naive sorting down to O(n).
- Whenever there exists a matching prefix in a group of strings, this monotonotic pattern can be made use to formulate hashing with binary search solution of suffix arrays.
- The idea of suffix arrays is very much similar to binary jumping, sparse table, and segment trees because all of them make use of 2’s powers.