Subsequence of a String

Problem Statement

You are given a string as an input. The task is to print all the possible subsequence of a string in any order.

Note: A subsequence is a string derived from the input string by deleting zero or more elements from the input string without changing the order of the remaining characters.

Example: str=”abcd”

• “ad” is a subsequence of str obtained by deleting ‘b’ and ‘c’.
• “ca” is not a subsequence of str because the order of elements is different from the input string.

Example

Let us understand the subsequence of string problem with the help of examples

Example1: str=”abc”

Output:

a
ab 
abc 
ac 
b 
bc 
c

Example2: str=”dd”

Output:

d
d
dd

Example Explanation

Example1: Subsequence are generated by deleting zero or more characters of the string without changing the order of the remaining elements. So first of all we will try to generate the subsequence by deleting zero characters. So when we delete zero characters then we get only one subsequence i.e “abc”. Now we try to generate the subsequence after deleting one character from the string. So we get three subsequence after deleting one character i.e “ab”,”ac”,”bc”. Now we try to generate the subsequence after deleting two characters from the string. So we get two subsequence after deleting two character i.e “a”,”b”,”c”. And when we try to generate the subsequence by deleting three characters then we get an empty string. So we are not required to print that. So we can delete maximum length-1 characters.

Example2: First of all, we will try to generate the subsequence by deleting zero characters. So when we delete zero characters then we get only one subsequence i.e “dd”. Now we try to generate the subsequence after deleting one character from the string. So we get two subsequence after deleting one character i.e “d”,”d”. And when we try to generate the subsequence by deleting two characters then we get an empty string. So we are not required to print that.

Input

You are given a string str as an input.

Output

You need to display all the subsequences of the input string. There is no restriction on the order of the subsequences, you can display subsequences in any order.

Constraints

0 <= str.length <= 100

Algorithm 1 – Pick and Don’t Pick Concept

Approach

In the Pick and Don’t Pick Concept of this problem, we pick the first character of the input string and append it to the output and call the subsequence function and this continues until the string becomes empty and then again calls the subsequence function without appending the first character in the output. This will also require to do until the input string does not become empty.

Algorithm

1. Given an input string input_str and for output, we use output_str.
2. Now remove the first character of input_str.
3. Call the subsequence function recursively appending the first character of input_str in an output_str.
4. When the input_str become empty then print the output_str and return.
5. After that call the subsequence function recursively by removing the first character of input_str without appending it into output_str.
6. This also continues till the string input_str become empty.

Implementation

C++ Implementation

// C++ program for the pick and don't approach
// of print all the subsequences of the string problem
#include <bits/stdc++.h>
using namespace std;

// Function to print all the subsequences
void printAllSubsequence(string input_str, string output_str){
	// Base Case
	//  If the input string is empty then simply print the output
	if (input_str.empty()) {
		cout << output_str << endl;
		return;
	}

	// output string is passed as a parameter by including first
	// character of the current input string
	// And input string is passed as a parameter 
	// by excluding the first character of current input string
	printAllSubsequence(input_str.substr(1), output_str + input_str[0]);

	// output string is passed as a parameter without 
	// including the first character of the 
	// current input string
	printAllSubsequence(input_str.substr(1), output_str);
}
// Driver code
int main(){
	// output string is declared as the blank
	//  before passing it to the function
	string output_str = "";
	string input_str = "abcd";
        // calling the function for printing
        // all subsequences of the string
	printAllSubsequence(input_str, output_str);

	return 0;
}

Output:

abcd
abc
abd
ab
acd
ac
ad
a
bcd
bc
bd
b
cd
c
d

Java Implementation

// Java program for the pick and don't approach
// of print all the subsequences of the string problem
class FindAllSubsequence{
    // Function to print all the subsequences
    static void printAllSubsequence(String input_str, String output_str){
        // Base Case
        //  If the input string is empty then simply print the output
        if (input_str.length()==0) {
            System.out.println( output_str );
            return;
        }
        // output string is passed as a parameter by including first
        // character of the current input string
        // And input string is passed as a parameter 
        // by excluding the first character of current input string
        printAllSubsequence(input_str.substring(1), output_str + input_str.charAt(0));
        // output string is passed as a parameter without 
        // including the first character of the 
        // current input string
        printAllSubsequence(input_str.substring(1), output_str);
    }
    // Driver code
    public static void main(String args[]){
        // output string is declared as the blank
        //  before passing it to the function
        String output_str = "";
        String input_str = "abcd";
        // calling the function for printing
        // all subsequences of the string
        printAllSubsequence(input_str, output_str);
    }
}

Output:

abcd
abc
abd
ab
acd
ac
ad
a
bcd
bc
bd
b
cd
c
d

Python Implementation

# Python program for the pick and don't approach
# of print all the subsequences of the string problem
# Function to print all the subsequences
def printAllSubsequence(input_str, output_str):
    
    # Base Case
    # If the input string is empty then simply print the output
    if len(input_str) == 0:
        print(output_str, end="\n")
        return
    # output string is passed as parameter by including first
    # character of the current input string
    # And input string is passed as a parameter
    # by excluding the first character of current input string
    printAllSubsequence(input_str[1:], output_str+input_str[0])
    
    # output string is passed as parameter without 
    # including the first character of the 
    # current input string
    printAllSubsequence(input_str[1:], output_str)


# Driver code
# output string is declared as the blank
# before passing it to the function
output_str = ""
input_str = "abcd"
# calling the function for printing
# all subsequences of the string
printAllSubsequence(input_str, output_str)

Output:

abcd
abc
abd
ab
acd
ac
ad
a
bcd
bc
bd
b
cd
c
d

Time Complexity

As the above recursive function is called total $2^{n}$ times as there are total $2^{n}$ subsequences of a string of length n. And in every function, we are doing work which takes a constant amount of time. So the complexity of every function is $O(1)$ and there are total of $2^{n}$ calls. So worst case time complexity of this approach is $O(2^{n})$.

Space Complexity

As we are using no extra space in this approach so space complexity is $O(1)$.

Algorithm 2- Recursive Approach by Removing Kth Character

Approach

In this approach, we will use a set to store all the subsequences. First of all, we will generate all the substrings of the string and then for every substring, we drop characters one by one and if the substring after dropping the character is not in the set then we again call the function recursively.

Algorithm

1. Start iterating over the input string input_str.
2. In every iteration start a nested loop for iterating the string from the end to generate the substrings.
3. Add every substring to the set.
4. Now start dropping characters from the substring.
5. If the string obtained after dropping the kth character is not in the set then recursively call the function.

Implementation

C++ Implementation

// C++ program for the recursive approach
// of print all the subsequences of the string problem
#include <bits/stdc++.h>
using namespace std;
// Declaring the set for storing all the subsequences of the string
unordered_set<string> subseq_store;

// Function to compute all the subsequence of the string
void printAllSubsequence(string input_str){
    // Start iterating over the entire string
    for (int i = 0; i < input_str.length(); i++) {
        // To generate substrings start iterating 
        // from end of the string
        for (int j = input_str.length(); j > i; j--) {
            string sub_string = input_str.substr(i, j);
            // insert every sub_string in the set
            subseq_store.insert(sub_string);
            // Drop kth character from the string
            for (int k = 1; k < sub_string.length(); k++) {
                string sb = sub_string;
                // Dropping kth character from the string
                sb.erase(sb.begin() + k);
                // if current string is not in set then call function
                if(subseq_store.find(sb) == subseq_store.end())
                    printAllSubsequence(sb);
            }
		}
	}
}
// driver code
int main() {
	string input_str = "abcd";
    // calling the function for computing
    // all subsequences of the string
	printAllSubsequence(input_str);
    // printing all the subsequences of the input string
    for(auto s:subseq_store)
        cout<<s<<"\n";
}

Output:

bcd
bc
abcd
acd
ab
a
abd
ad
d
ac
cd
c
b
bd
abc

Java Implementation

// Java program for the recursive approach
// of print all the subsequences of the string problem
import java.util.*;
class FindAllSubsequence{
    // Declaring the set for storing all the subsequences of the string
    static HashSet<String> subseq_store=new HashSet<>();
    // Function to compute all the subsequences of the string
    static void printAllSubsequence(String input_str) {
        // Start iterating over the entire string
        for (int i = 0; i < input_str.length(); i++) {
            // To generate substrings start iterating 
            // from end of the string
            for (int j = input_str.length(); j > i; j--) {
                String sub_string = input_str.substring(i, j);
                // insert every sub_string in the set
                subseq_store.add(sub_string);
                // Drop kth character from the string
                for (int k = 1; k < sub_string.length(); k++) {
                    StringBuilder sb = new StringBuilder(sub_string);
                    // Dropping kth character from the string
                    sb.deleteCharAt(k);
                    // if current string is not in set then call function
                    if(!subseq_store.contains(sb.toString()))
                        printAllSubsequence(sb.toString());
                }
            }
        }
    }
    // driver code
    public static void main(String args[]) {
        String input_str = "abcd";
        // calling the function for computing
        // all subsequences of the string
        printAllSubsequence(input_str);
        // printing all the subsequences of the input string
        for(String s:subseq_store)
            System.out.println(s);
    }
}

Output:

a
cd
ab
bc
ac
abd
b
bd
bcd
acd
ad
c
abc
d
abcd

Python Implementation

# Python program for the recursive approach
# of print all the subsequences of the string problem

# Declaring the set for storing all the subsequences of the string
subseq_store = set()

# Function to compute all the subsequences of the string
def printAllSubsequence(input_str):

	# Start iterating over the entire string
	for i in range(len(input_str)):

		# To generate substrings start iterating 
		# from end of the string
		for j in range(len(input_str),i,-1):
			sub_string = input_str[i: i+j]
                       # insert every sub_string in the set
			subseq_store.add(sub_string)

			# Drop kth character from the substring
			for k in range(1,len(sub_string)):
				sb = sub_string

				# Dropping kth character from the string
				sb = sb.replace(sb[k],"")
				printAllSubsequence(sb)

# Driver Code

input_str = "abcd"
# calling the function for computing
# all subsequences of the string
printAllSubsequence(input_str)
# printing all the subsequences of the input string
for s in subseq_store:
	print(s,end = "\n")

Output:

bd
acd
ad
c
ac
abcd
cd
abd
d
b
abc
bcd
a
ab
bc

Time Complexity

As in the above function, we are iterating over the string of length n and we are using a nested loop for an iterating string from the end. So for iterating two nested loops, the worst-case time complexity is $O(n^{2})$. And in every iteration we are inserting an element into the set, for inserting an element into the set time complexity is $O(logn)$ and we are iterating over substring for dropping character which has $O(n)$ worst-case complexity. So total time complexity of the function is $O(n^{2})O(n)O(logn)$ = $O(n^{3}logn)$ and total $n^{2}$ times function is called. So worst case complexity of this approach is $O(n^{5}logn)$

Space Complexity

As we are storing all subsequences in a set and the total number of subsequences are $2^{n}$. So space complexity is $O(2^{n})$.

Algorithm 3- Recursive Approach – by Fixing One Character and Making Subgroup

Approach

In this approach, we are fixing one character of the string at a time and then adding other characters for generating the subsequence of a string and if the current string length is not equal to zero then we print that string.

Algorithm

1. Start a loop for iterating over the string.
2. Add the present index character to the string and then call the recursive function for the new string.
3. If current string length is not equal to zero then print that string.
4. After returning from the recursive function remove the last character of the current string.

Implementation

C++ Implementation

// C++ program for the recursive approach
// of print all the subsequences of the string problem
#include <bits/stdc++.h>
using namespace std;
// Function to print all the subsequences of the string
void printAllSubsequence(string input_str, int length, int index = -1,string cur_str = ""){
    // base case of the recursive function
    if (index == length)
        return;
    // Printing the subsequence of the string
    if (!cur_str.empty()) {
        cout << cur_str << "\n";
    }
    for (int i = index + 1; i < length; i++) {
        // appending current index character to the cur_str
        cur_str += input_str[i];
        // recursive call for function 
        printAllSubsequence(input_str, length, i, cur_str);
        // backtracking
        cur_str = cur_str.erase(cur_str.size() - 1);
    }
    return;
}
// Driver code
int main(){
    string input_str = "abcd";
    // calling the function for printing
    // all the subsequences of the string
    printAllSubsequence(input_str,input_str.size());
    return 0;
}

Output:

a
ab
abc
abcd
abd
ac
acd
ad
b
bc
bcd
bd
c
cd
d

Java Implementation

// Java program for the recursive approach
// of print all the subsequences of the string problem
class FindAllSubsequence {
    // Function to print all the subsequences of the string
    static void printAllSubsequence(String input_str, int length, int index, String cur_str){
        // base case of the recursive function
        if (index == length) {
            return;
        }
        // Printing the subsequence of the string
        if (cur_str != null && !cur_str.trim().isEmpty()) {
            System.out.println(cur_str);
        }
        int i;
        for (i = index + 1; i < length; i++) {
            // appending current index character to the cur_str
            cur_str += input_str.charAt(i);
            // recursive call for function 
            printAllSubsequence(input_str, length, i, cur_str);
            // backtracking
            cur_str = cur_str.substring(0, cur_str.length() - 1);
        }
    }
    // Driver code
    public static void main(String[] args){
        String input_str = "abcd";
        // calling the function for printing
        // all the subsequences of the string
        printAllSubsequence(input_str,input_str.length(),-1,"");
    }
}

Output:

a
ab
abc
abcd
abd
ac
acd
ad
b
bc
bcd
bd
c
cd
d

Python Implementation

# Python program for the recursive approach
# of print all the subsequences of the string problem
def printAllSubsequence(input_str, length, index, cur_str):
    # base case of the recursive function
    if index == length:
        return
    # Printing the subsequence of the string
    if (not len(cur_str)) == 0:
        print(cur_str, end = "\n")
    for i in range(index + 1, length):
        # appending current index character to the cur_str
        cur_str += input_str[i]
        # recursive call for function 
        printAllSubsequence(input_str, length, i, cur_str)
        # backtracking
        cur_str = cur_str[0:len(cur_str) - 1]
    return
# Driver code
input_str = "abcd"
# calling the function for printing
# all the subsequences of the string
printAllSubsequence(input_str, len(input_str), -1, "")

Output:

a
ab
abc
abcd
abd
ac
acd
ad
b
bc
bcd
bd
c
cd
d

Time Complexity

Here we are using the concept of backtracking for finding the subsequence of a string. The worst-case time complexity of this approach of the subsequence of a string problem is $O(2^{n})$.

Space Complexity

As we are not using any extra space So space complexity of this approach is $O(1)$.

Algorithm 4- Using Bit Manipulation

Approach

In this approach, we are using bit manipulation to print all subsequences of a string. We will consider all the numbers from 0 to $2^{n}$ and for every number, we will check the set bits(1) and we pick only those index characters for which we have set bit. In this, every number gives us a subsequence. And all the subsequence of a string is generated.

Refer to the below image to visualize the bit manipulation approach of the subsequence of a string problem.

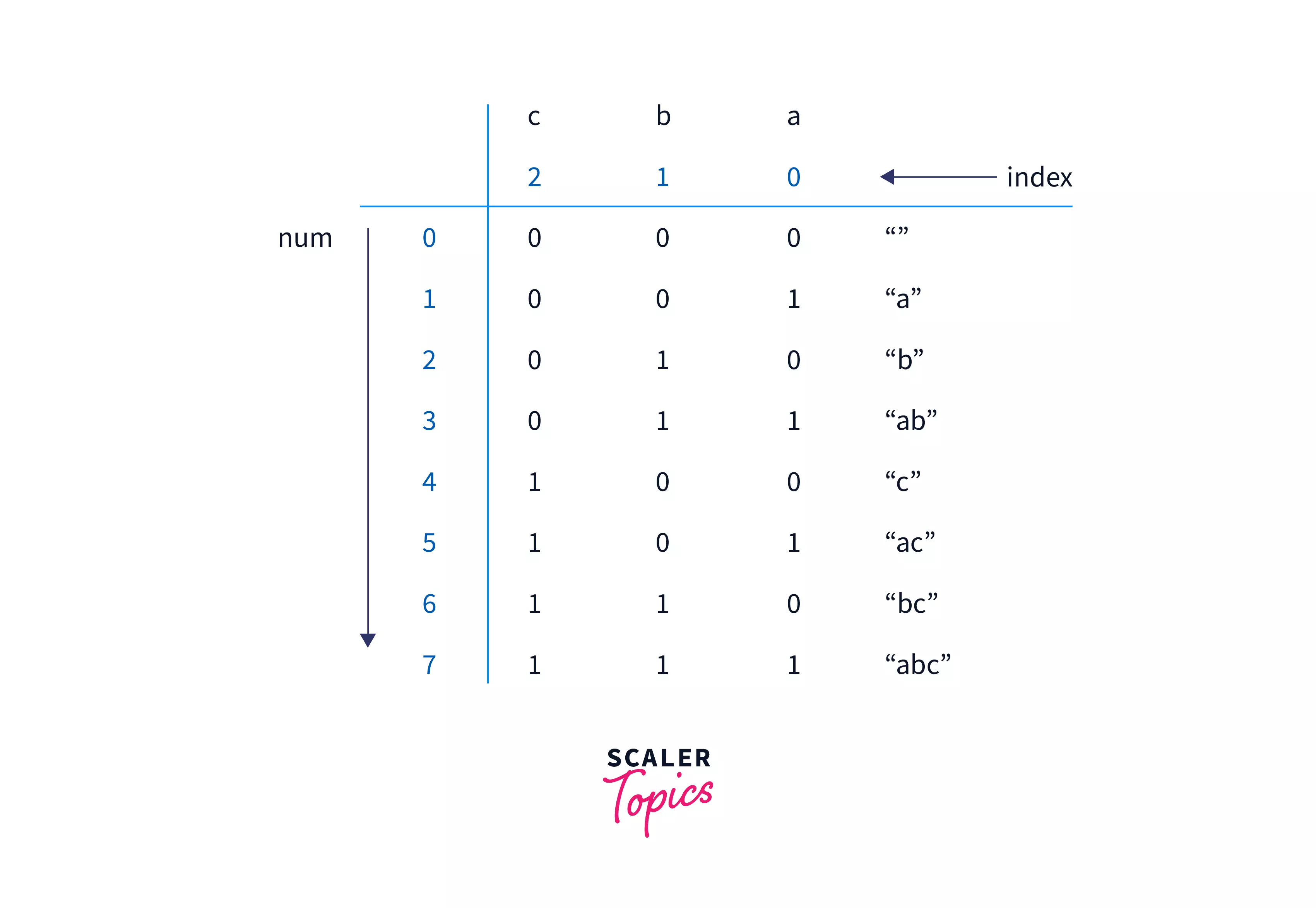
Algorithm

1. Declaring the list output for storing all the substrings.
2. Start a loop from 0 to $2^{len}$ i.e (1<<len) using the variable num.
3. For every value of num iterate a loop for the length of the string to check if the ith bit is set.
4. If the ith bit is set then we will add that character into the string.
5. If the string obtained after the inner loop has a length greater than zero then add that string into the resultant list.

Now first of all let us understand << operator.

Note:
<<
<< is a left shift operator.
x << y left shifts the bits of x operand by y number of places. And left shifting an integer x by y gives us a result equivalent to $x2^{y}$. ::: :::section{.main} Example: 5<<2 = 20 Binary conversion of 5: 00000101 When we left shifts the bits of 5 by 2 places then we get: 00010100 Decimal conversion of result: 20 $1<2^{len}$

Implementation

C++ Implementation

// C++ program for the bit manipulation approach
// of print all the subsequences of the string problem
#include<bits/stdc++.h>
using namespace std;
// Function to compute all the subsequences
vector<string> printAllSubsequence(string input_str) {
    // getting the length of the input string
	int len = input_str.length();
    // creating vector for storing the subsequences of input string.
	vector<string>output;
	for (int num = 0; num < (1 << len); num++) {
        // initializing a string to store sub string
		string sub_str = "";
		for (int i = 0; i < len; i++) {
			// check whether ith bit is set or not
			if (num & (1 << i)) {
				sub_str += input_str[i];
			}
		}
        // if length of sub string is greater than zero then store in output vector
		if (sub_str.length() > 0) {
			output.push_back(sub_str);
		}
	}
    // returning the output vector
	return output;
}
//driver code
int main(){
	string input_str="abcd";
	vector<string> output = printAllSubsequence(input_str);
    // iterating over the vector to
	// print all the subsequence of input string.
	for (auto it : output) {
		cout << it << "\n";
	}

}

Output:

a
b
ab
c
ac
bc
abc
d
ad
bd
abd
cd
acd
bcd
abcd

Java Implementation

// Java program for the bit manipulation approach
// of print all the subsequences of the string problem
import java.util.*;
class Main{
    // Function to compute all the subsequences
    static ArrayList<String> printAllSubsequence(String input_str) {
        // getting the length of the input string
        int len = input_str.length();
        // creating List for storing the subsequences of input string.
        ArrayList<String> output=new ArrayList<>();
        for (int num = 0; num < (1 << len); num++) {
            // initializing a string to store sub string
            String sub_str = "";
            for (int i = 0; i < len; i++) {
                // check whether ith bit is set or not
                if ((num & (1 << i))!=0) {
                    sub_str += input_str.charAt(i);
                }
            }
            // if length of sub string is greater than zero then store in output vector
            if (sub_str.length() > 0) {
                output.add(sub_str);
            }
        }
        // returning the output list
        return output;
    }
    //driver code
    public static void main(String args[]){
        String input_str="abcd";
        ArrayList<String> output = printAllSubsequence(input_str);
        // iterating over the list to
        // print all the subsequence of input string.
        for (String s : output) {
            System.out.println(s);
        }
    }
}

Output:

a
b
ab
c
ac
bc
abc
d
ad
bd
abd
cd
acd
bcd
abcd

Python Implementation

# Python program for the bit manipulation approach
# of print all the subsequences of the string problem
# Function to compute all the subsequences
def printAllSubsequence(input_str):
    # getting the length of the input string
    len1 = len(input_str)
    # creating empty list for storing the subsequences of input string.
    output = []
    num = 0
    while num < (1 << len1):
        # initializing a string to store sub string
        sub_str = ""
        for i in range(0, len1):
            # check whether ith bit is set or not
            if (num & (1 << i)) != 0:
                sub_str += input_str[i]
        # if length of sub string is greater than zero then store in output vector
        if len(sub_str) > 0:
            output.append(sub_str)
        num += 1
    # returning the output list
    return list(output)       
#driver code
input_str = "abcd"
output = printAllSubsequence(input_str)
# iterating over the list to
# print all the subsequence of input string.
for s in output:
    print(s, end = '')
    print("\n", end = '')

Output:

a
b
ab
c
ac
bc
abc
d
ad
bd
abd
cd
acd
bcd
abcd

Time Complexity

As there are two nested loops and the outer loop runs $2^{n}$ times and the inner loop is running n times. Here n is the length of the string. So total time complexity is $O(2^{n})O(n)$. So worst case time complexity of this approach is $O(n2^{n})$.

Space Complexity

As we are storing all the subsequence of a string in a list and there is a total $2^{n}$ of the string of length n. So space complexity of this approach of the subsequence of a string problem is $O(2^{n})$.

Conclusion

• In the subsequence of a string problem we are required to print all the subsequences of the string.
• A subsequence is a string derived from the input string by deleting zero or more elements from the input string without changing the order of the remaining characters.
• In Pick and Don’t Pick Concept of the subsequence of a string, to generate the subsequence we recursively call the function by appending the current character and without appending the current character.
• In fix one character and making a subgroup approach, we are fixing one character of the string at a time and then adding other characters for generating the subsequence of a string.
• In removing Kth character approach, we generate all the substring of the string and then drop characters one by one from the substring to generate subsequences and store each subsequence in the set.
• In the bit manipulation approach of this problem, we set and reset the bits to print the subsequence.

FAQs

Q.Which is the best method among the 4 to get all subsequences of the string?

A.If we talk about the best approach to get all the subsequences of the, then it is dependent on our requirements. If we require to use the optimal solution in terms of time complexity and not to use extra space for storing the subsequence then we can use the pick and don’t pick approach or we can use fix one character and make a subgroup approach.