Strongly connected components (SCC's) are directed graph or a part of a directed graph in which each and every node is reachable from one another or in other words, there is a path between each and every vertex. There are many ways to find strongly connected components in any graph with the most efficient algorithm being Tarjan’s Algorithm which uses DFS to find strongly connected components.
Takeaways
A strongly connected component(SCC) in a directed graph is either a cycle or an individual vertex.
What are Strongly Connected Components?
The directed graph is said to be strongly connected if you can reach any vertex from any other vertex within that component. A single directed graph may contain multiple strongly connected components
Connectivity in a graph represents whether two vertices are reachable from each other or not. Now if we define connectivity in terms of path, then we can say two vertices are connected if there is a path from one vertex to the other.
In the case of an undirected graph, this connectivity is simple as if Vertex_1 is reachable from Vertex_2 then Vertex_2 is also reachable from Vertex_1, but in directed graphs these things are quite different.
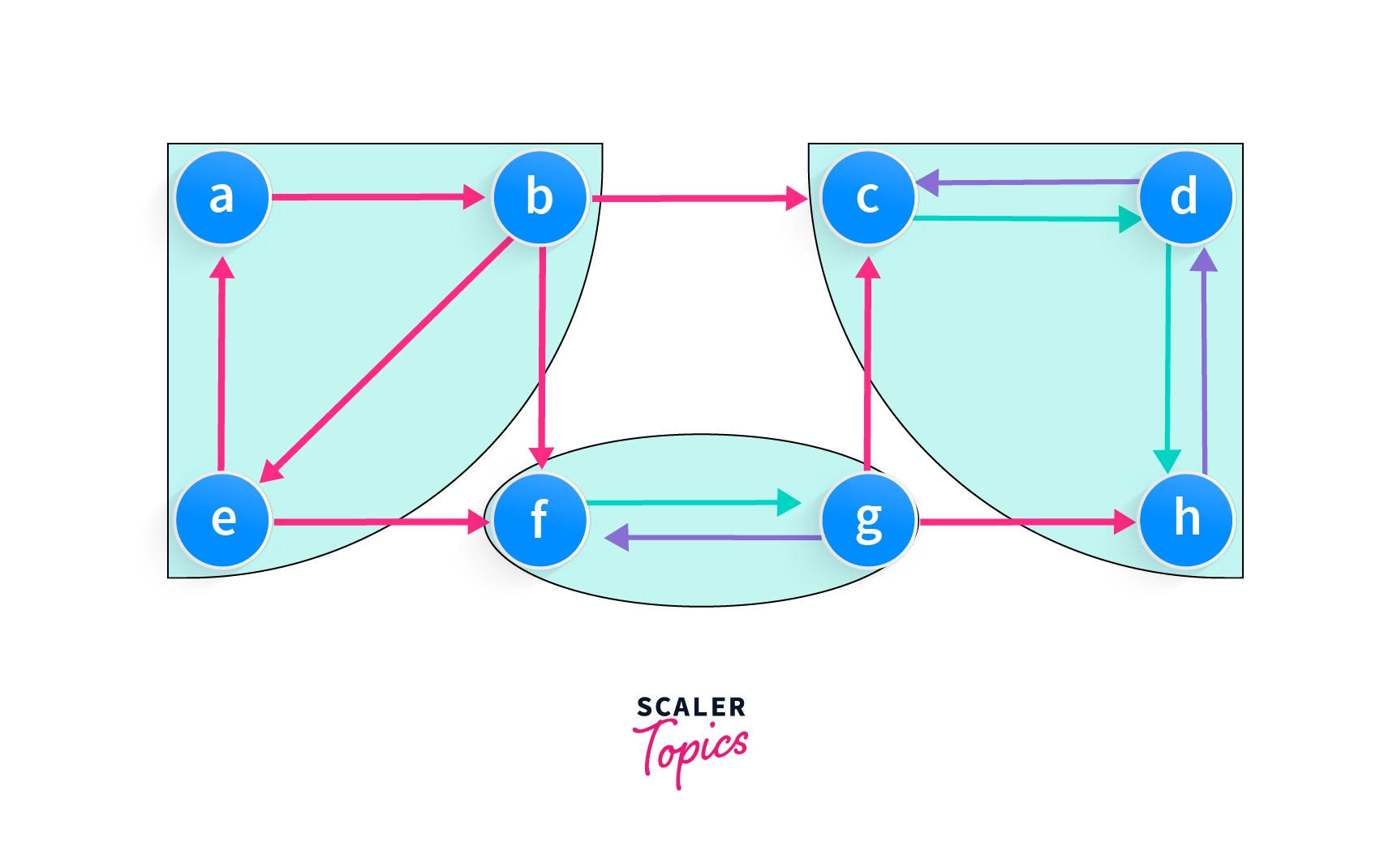
The directed graph is said to be strongly connected if you can reach any vertex from any other vertex within that component. A single directed graph may contain multiple strongly connected components. For example, the below given graph contains 3 strongly
Components(highlighted ones) that are: {a,b,e,f}, {f,g} and {c,d,g,h} because in all of these components there is a path from one vertex to every other vertex.
How to Find Strongly Connected Components
Brute force approach of finding Strongly Connected Components
Now the next question is how to find strongly connected components. Suppose we have a graph with N number of vertices. Now the basic approach is to check for every node 1 to N vertex one by one for strongly connected components since each vertex has a possibilty of being in Strongly Connected Component.
In order to check whether a given element is forming a strongly connected component, we will visit each vertex and then we will perform DFS from that vertex and check wether we are able to reach each vertex from that or not.
For example, suppose we have a graph of N vertices placed on INDEX_1, INDEX_2, INDEX_3 and so on. Now we pick the element at INDEX_1 to check whether it is forming a strongly connected component or not. In order to check that, we will traverse all the elements from INDEX_2 to INDEX_N and check for each element whether we can reach INDEX_1 element or not.
Similarly we will check from the INDEX_1 element that we can reach element INDEX_2 to INDEX_N or not. This will help in finding the strongly connected component having an element at INDEX_1. In order to find all the strongly connected components in the graph, we will have to perform this operation for each vertex.
Time and Space Complexity of Brute Force Approach
Time Complexity:
The time complexity of the above algorithm is O(V^3), where V is the number of vertices in the graph. Since we are iterating upon each vertices three times in order to check wether it is forming a strongly connected component or not.
Space Complexity:
The space complexity will be O(1), since we are not using any extra space.
As we have discussed the time complexity of brute force approach is very high thus we need some optimised algorithm to find strongly connected components. There are multiple ways of finding them but the most efficient is Tarjan’s Algorithm.
Tarjans’s Algorithm
Before coming to the algorithm, we need to take into account two points related to DFS of strongly connected components:
1- In the DFS of a graph containing strongly connected components, the strongly connected components form a subtree of the DFS tree.
2- If we somehow find the head of such a subtree then we can then all the nodes in that subtree will be a part of a strongly connected component.
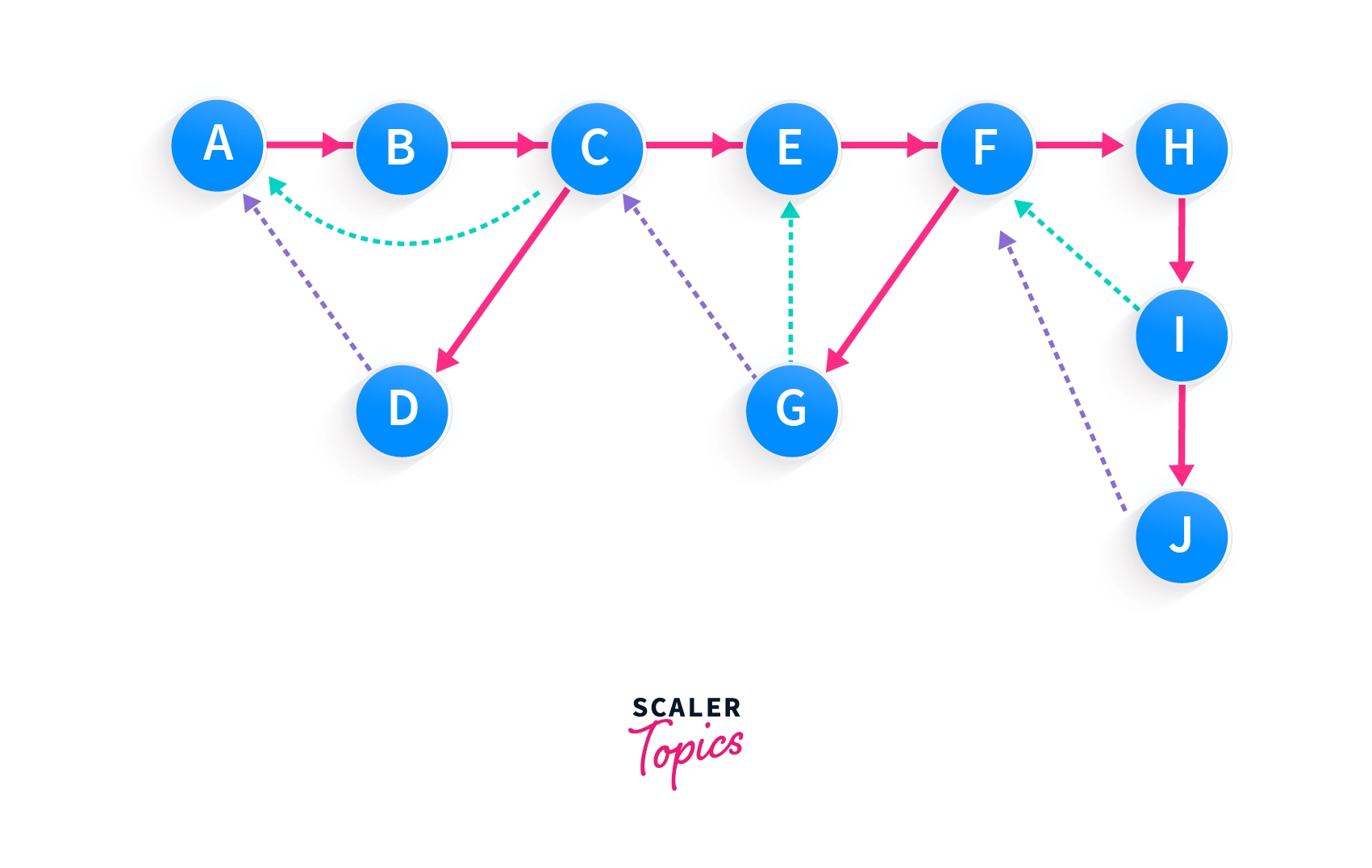
In the diagram given below, if we observe closely we can see that A,C and F are forming 3 roots of DFS tree and by traversing the nodes connected by these roots we can get the strongly connected components associated with the respective roots.
Let us now discuss two termilogies that will be required in the Tarjan's algorithm that is low and disc.
disc represents the instance at which the node entered into DFS traversal for the first time.
In the above example the disc of A,B and J are 1,2 and 10 respectively.
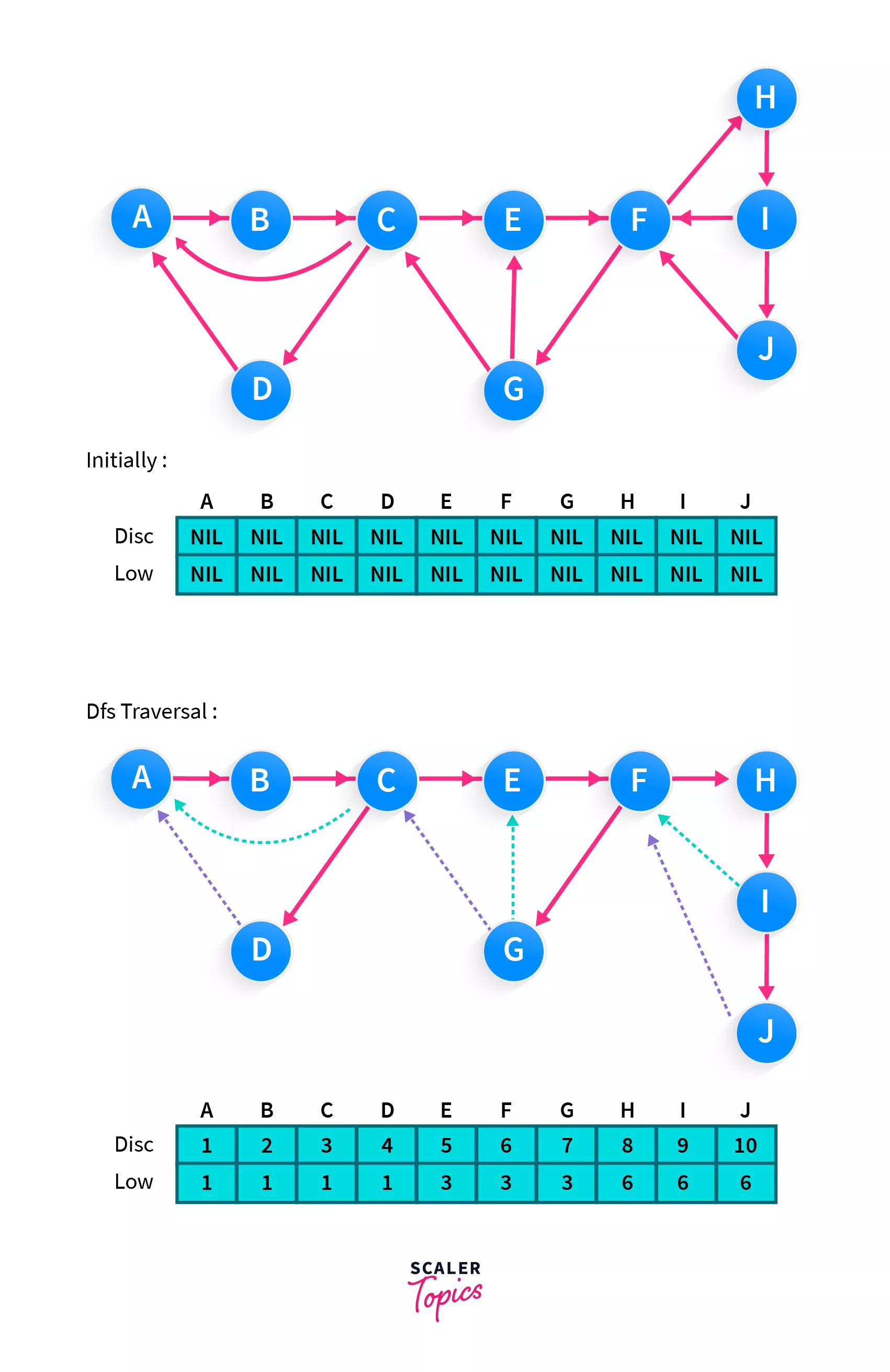
low represents the lowest disc value node that our present node can reach. Initially the low and disc value of all the nodes will be same but it might happen that while doing DFS traversal our node has a path to some node having lower disc value.
Now in that case we will take lowest possible disc value. In the above graph low value of A,B and J will be 1,1 and 6.
Now the next comes that why we need low and disc value. As we discussed earlier we can find the strongly connected components if we get head or root node of DFS substree having strongly connected components. This head node has one special property that is:
low[head]= disc[head]Because, in this case we cannot reach any previously visited nodes from u, thus all the nodes in the subtree rooted at u, can be reached to u and similarly, u can be reached from those nodes.
Now by taking the help of these two arrays we will implement the Tarjan’s algorithm.
Given below is the code of Tarjan's Algorithm. In this code we will use a stack and push the vertices into it as they are discovered in the DFS traversal and will also keep updating the low and disc value of each vertices.
Now whenever we will encounter a situation where low[u]= head[u], we will know that this is the head of one strongly connected component. Thus we will output it in our answer.
Implementation of Tarjan’s Algorithm in C++ and JAVA
C++
#include<iostream>
#include<stack>
#define v 5
using namespace std;
int graph[v][v];
int min(int a, int b) {
return (a < b) ? a : b;
}
void findComponent(int u, int disc[], int lowLink[], stack < int > & stk, bool stkItem[]) {
static int time = 0;
disc[u] = lowLink[u] = ++time;
stk.push(u);
stkItem[u] = true;
for (int v = 0; v < v; v++) {
if (graph[u][v]) {
if (disc[v] == -1) {
findComponent(v, disc, lowLink, stk, stkItem);
lowLink[u] = min(lowLink[u], lowLink[v]);
} else if (stkItem[v])
lowLink[u] = min(lowLink[u], disc[v]);
}
}
int poppedItem = 0;
if (lowLink[u] == disc[u]) {
while (stk.top() != u) {
poppedItem = stk.top();
cout << poppedItem << " ";
stkItem[poppedItem] = false;
stk.pop();
}
poppedItem = stk.top();
cout << poppedItem << endl;
stkItem[poppedItem] = false;
stk.pop();
}
}
void strongConComponent() {
int disc[v], lowLink[v];
bool stkItem[v];
stack < int > stk;
for (int i = 0; i < v; i++) {
disc[i] = lowLink[i] = -1;
stkItem[i] = false;
}
for (int i = 0; i < v; i++)
if (disc[i] == -1)
findComponent(i, disc, lowLink, stk, stkItem);
}
int main() {
strongConComponent();
}JAVA
public List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
int[] disc = new int[n], low = new int[n];
List<Integer>[] graph = new ArrayList[n];
List<List<Integer>> res = new ArrayList<>();
Arrays.fill(disc, -1);
for (int i = 0; i < n; i++) {
graph[i] = new ArrayList<>();
}
// build graph
for (int i = 0; i < connections.size(); i++) {
int from = connections.get(i).get(0), to = connections.get(i).get(1);
graph[from].add(to);
graph[to].add(from);
}
for (int i = 0; i < n; i++) {
if (disc[i] == -1) {
dfs(i, low, disc, graph, res, i);
}
}
return res;
}
int time = 0; // time when discover each vertex
private void dfs(int u, int[] low, int[] disc, List<Integer>[] graph, List<List<Integer>> res, int pre) {
disc[u] = low[u] = ++time; // discover u
for (int j = 0; j < graph[u].size(); j++) {
int v = graph[u].get(j);
if (v == pre) {
continue; // if parent vertex, ignore
}
if (disc[v] == -1) { // if not discovered
dfs(v, low, disc, graph, res, u);
low[u] = Math.min(low[u], low[v]);
if (low[v] > disc[u]) {
// u - v is critical, there is no path for v to reach back to u or previous vertices of u
res.add(Arrays.asList(u, v));
}
} else { // if v discovered and is not parent of u, update low[u], cannot use low[v] because u is not subtree of v
low[u] = Math.min(low[u], disc[v]);
}
}
}Time and Space Complexity of Tarjan’s Algorithm
Time Complexity:
We are performing DFS in this algorithm and then performing a constant amount of work in each iteration. Thus the time complexity will be the same as that of DFS, that is O (V + E), where V is the number of vertices and E is the number of edges in the graph.
Space Complexity:
Talking about the space complexity, since it is a DFS based algorithm thus at any time a maximum number of V nodes will be stored in a stack. Thus space complexity will be O( V ).
Kosaraju’s Algorithm
Kosaraju’s algorithm is a method used to find strongly connected components (SCCs) in a directed graph. The algorithm is named after S. Rao Kosaraju, who described it in 1978. It consists of two main steps:
- First DFS (Depth-First Search): In the first step, the algorithm performs a depth-first search on the given graph and keeps track of the order in which vertices finish their exploration.
- Second DFS: In the second step, the algorithm performs another depth-first search, but this time on the transpose of the original graph (reversed direction of all edges), using the order obtained in the first step. This step helps to identify the strongly connected components.
Here’s a general outline of how Kosaraju’s algorithm works:
- Perform a DFS traversal on the original graph, keeping track of the finishing times of vertices.
- Reverse all the edges of the original graph to obtain the transpose graph.
- Perform DFS on the transpose graph, in the order of decreasing finishing times obtained in step 1.
- Each tree in the DFS forest formed in step 3 represents a strongly connected component.
This algorithm runs in linear time, making it efficient for finding strongly connected components in large graphs.
C++ Code:
#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>
using namespace std;
class Graph {
int V;
vector<vector<int>> adj;
vector<bool> visited;
stack<int> finishedVertices;
public:
Graph(int vertices) : V(vertices) {
adj.resize(V);
visited.resize(V, false);
}
void addEdge(int u, int v) {
adj[u].push_back(v);
}
void DFS1(int v) {
visited[v] = true;
for (int u : adj[v]) {
if (!visited[u]) {
DFS1(u);
}
}
finishedVertices.push(v);
}
void DFS2(int v) {
visited[v] = true;
cout << v << " ";
for (int u : adj[v]) {
if (!visited[u]) {
DFS2(u);
}
}
}
void reverseEdges() {
vector<vector<int>> newAdj(V);
for (int i = 0; i < V; ++i) {
for (int u : adj[i]) {
newAdj[u].push_back(i);
}
}
adj = newAdj;
}
void findSCCs() {
for (int v = 0; v < V; ++v) {
if (!visited[v]) {
DFS1(v);
}
}
fill(visited.begin(), visited.end(), false);
reverseEdges();
while (!finishedVertices.empty()) {
int v = finishedVertices.top();
finishedVertices.pop();
if (!visited[v]) {
cout << "SCC: ";
DFS2(v);
cout << endl;
}
}
}
};
int main() {
Graph g(5);
g.addEdge(1, 0);
g.addEdge(0, 2);
g.addEdge(2, 1);
g.addEdge(0, 3);
g.addEdge(3, 4);
cout << "Strongly Connected Components:\n";
g.findSCCs();
return 0;
}This code defines a Graph class to represent a directed graph. It includes methods to add edges, perform DFS for both steps of Kosaraju’s algorithm, reverse edges, and find strongly connected components. In the main() function, a sample graph is created and SCCs are printed out. You can modify the main() function to create your own graph and test the algorithm.
Time and Space complexity of Kosaraju’s Algorithm
Time Complexity:
In kosaraju algorithm mainly three steps takes place :
DFS is called : Time taken to perform DFS on graph represented by adjacency list is O(V+E).
Graph represented by adjacency list is reversed: For reversing the graph represented using adjacency list we have to iterate over the adjacency list which will take O(V) time.
Again DFS is called : TIme taken for DFS on graph represented by adjacecny list is O(V+E)
So, the total time taken in all the three steps in kosaraju algorithm is O(V+E) +O(V) +O(V+E) = O(V+E)
So, the time comlexity of the kosaraju algorithm is O(V+E).
Space Complexity:
As kosaraju algorithm uses stack to store the vertices while performing first DFS so the space used by stack is equal to size of the vertices of the graph. So, the time complexity of kosaraju’s algorithm is O(N), where N is the total no of vertices in the graph.
Applications of Strongly Connected Components
Strongly connected components are used in many of the algorithms and problems as an immediate step.
Strongly connected componentsare used to solve 2-satisfiability problems.Strongly connected componentsare used to computer Dulmage–Mendelsohn decomposition- In the social networking sites, strongly connected components are used to depict the group of people who are friends of each other or who have any common interest.
- It can also be used to convert a graph into a Direct Acyclic graph of strongly connected components.
Conclusion
Strongly connected componentsrepresents a graph where there is a path between each pair of vertex- Tarjan’s algorithm is the most efficient algorithm to find strongly connected components
- In Tarjan’s algorithm we perform only one DFS traversal thus time complexity is
O(1) Strongly connected componentshave many real life applications like representing groups in social media platforms etc.