State Space Reduction in Dynamic Programming

State space reduction is the process that is used to decrease the number of states in a dynamic programming solution in an optimal way. It is specific to a given problem and usually involves reducing the size of its dimensions by a constant value.

Scope of Article

• The article will help you understand dynamic programming, the concept of state and how state space can be reduced.
• You will also learn how reduction of state space can help provide more optimal solutions to problems.
• This article doesn’t cover every application of state space reduction.

Takeaways

The primary principle of dynamic programming is to prevent repetitive effort by remembering partial outcomes, and this approach is used in a variety of real-world scenarios.

Introduction

Ever played the Memory Train game? The rules are pretty simple. You say a word and the next person adds another word to yours, and the next to that queue. For example, consider the following image. A says the word ‘The’ to B. B adds ‘Brown’ and thus tells C ‘The Brown’. Similarly each child adds a word to the existing queue.

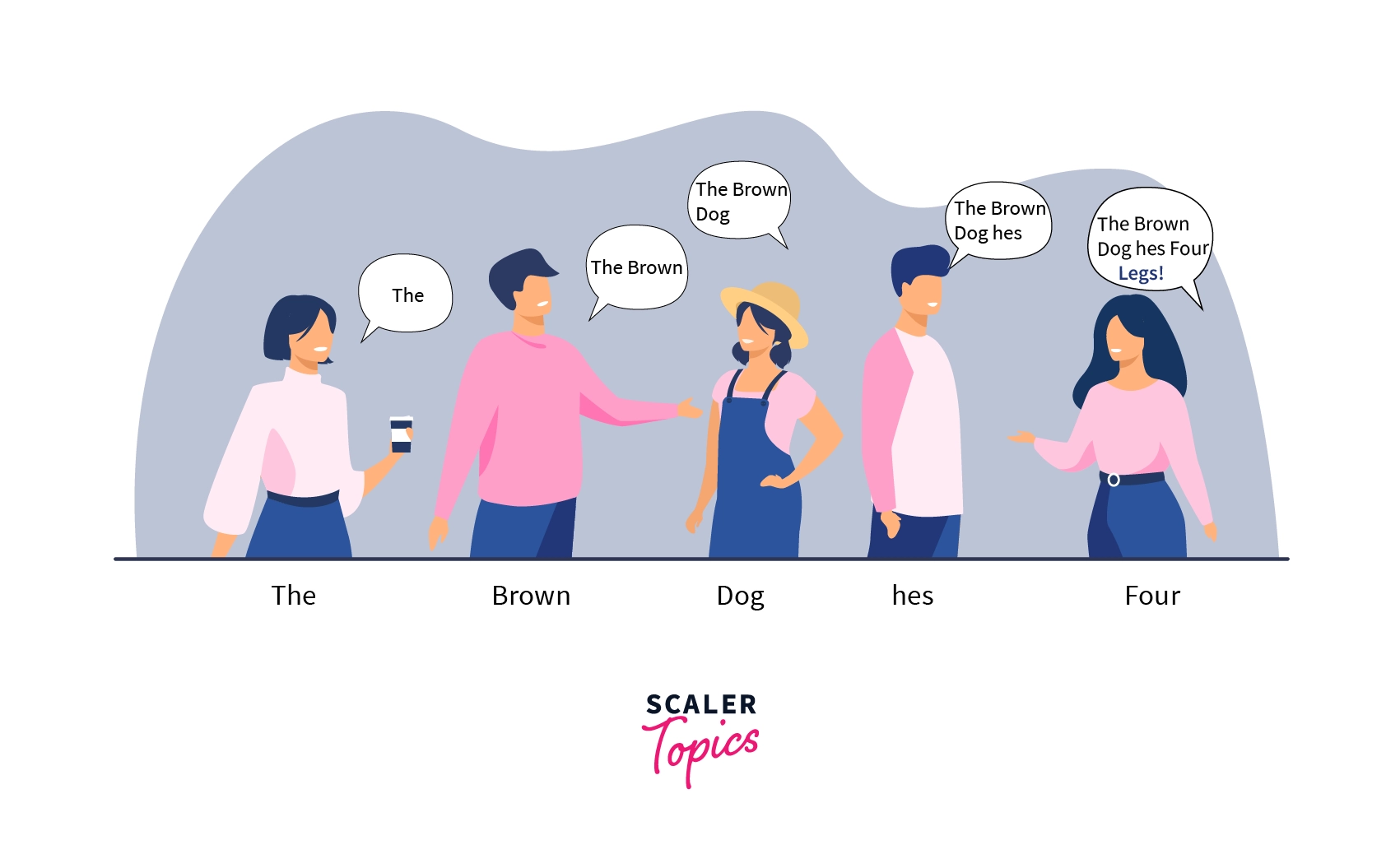
Dynamic programming follows a similar logic. In dynamic programming, we divide a problem into overlapping sub-problems and work our way up to larger and larger sub-problems. In such circumstances, you discover that there are some overlapping sub-problems and then preserve the result so that it may be utilized later in the event of overlapping.

Assume we have a machine, and we have some quantities known as state variables that we may use to identify its state at time t. There will be moments when we must make a decision that impacts the condition of the system, which we may or may not be aware of in advance. These decisions or adjustments are similar to state variable transformations.

The primary principle of Dynamic Programming is to prevent repetitive effort by remembering partial outcomes, and this approach is used in a variety of real-world scenarios. State space reduction is used to improve the space and time complexity of dynamic programming.

Reducing the Number of States

There are several techniques to limit the number of states in a dynamic programming solution. One approach is to try to lower the size of one of the current dimensions. The total time complexity of the solution remains the same when the size is lowered by some amount, but the constant factor improves. The most substantial gain can be obtained by totally eliminating a dimension or lowering its size to a tiny constant.

The exact approach of shrinking the state space varies depending on the task. There is no universal solution that can be applied to all issues. However, one general idea worth mentioning is that the number of dimensions can be reduced if there are some dimensions capturing the same information, or if there is a dimension capturing irrelevant information. The best way to gain intuitions for such ideas to enhance existing dynamic programming solutions is to read more and more combat stories.

Problem

Let’s consider the simple scenario of calculating binomial coefficients. A binomial coefficent C(n,k) gives number of ways in which k objects can be chosen from a set of n objects, irrespective of the order. A binomial coefficient C(n, k) can be defined as the coefficient of x^k in the expansion of (1 + x)^n.

For this problem, we wil have to create a function with 2 parameters n and k that returns the value of Binomial Coefficient C(n,k).

The formula of Binomial Coefficient is as given below:

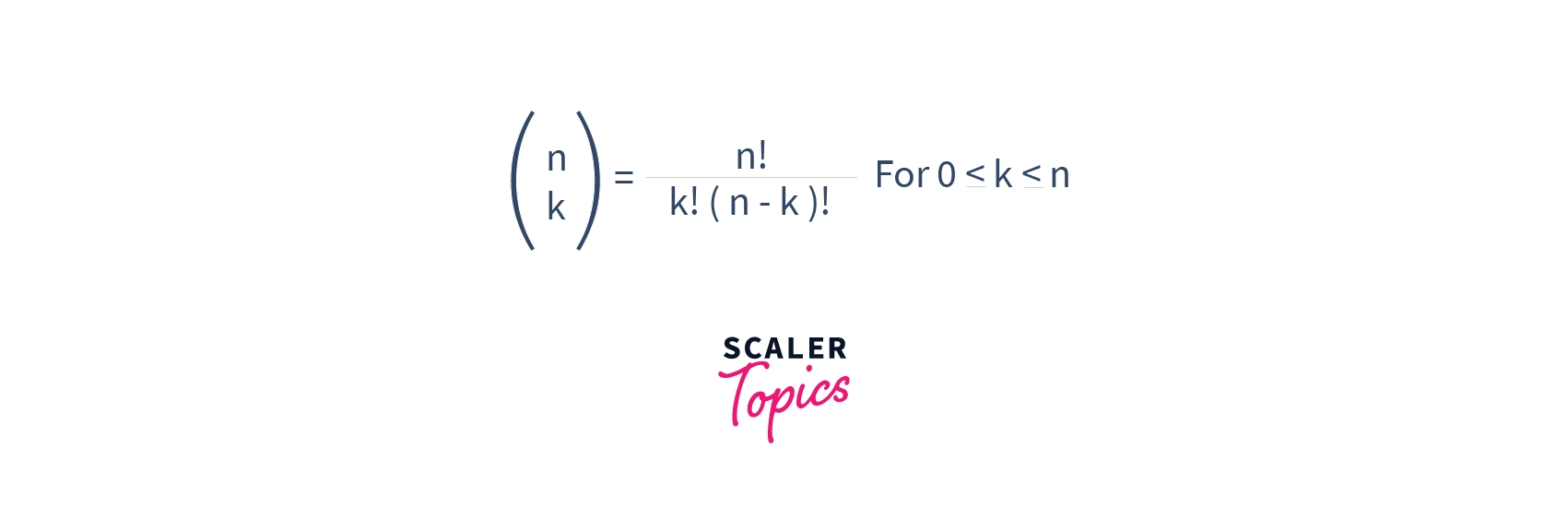
For example, if n=5 and k=3, the function should return a 10.

Initial Solution

When you talk about Binomial Coefficient, the first solution that runs through your mind is that of recursion. If we were to use recursion, the function will calculate binomial coefficient as follows:

C(n, k) = C(n-1, k-1) + C(n-1, k)
C(n, 0) = C(n, n) = 1

We would write the function in C++ as:

int binCoeffrec(int n, int k)
{
    if (k > n)
        return 0;
    if (k == 0 || k == n)
        return 1;

    return binomialCoeff(n - 1, k - 1) + binomialCoeff(n - 1, k);
}

Here, both the time and space complexity depend heavily on the values of k and n and can be given by:
Time Complexity: O(n * max(k,n-k))
Space Complexty: O(n * max(k,n-k))

Solution using Dynamic Programming

If you draw a recursion tree for the code shown above, you will realize that there is a redundancy in subproblems. Whenever there are overlapping subproblems like this, we can use Dynamic Programming to increase the efficiency.

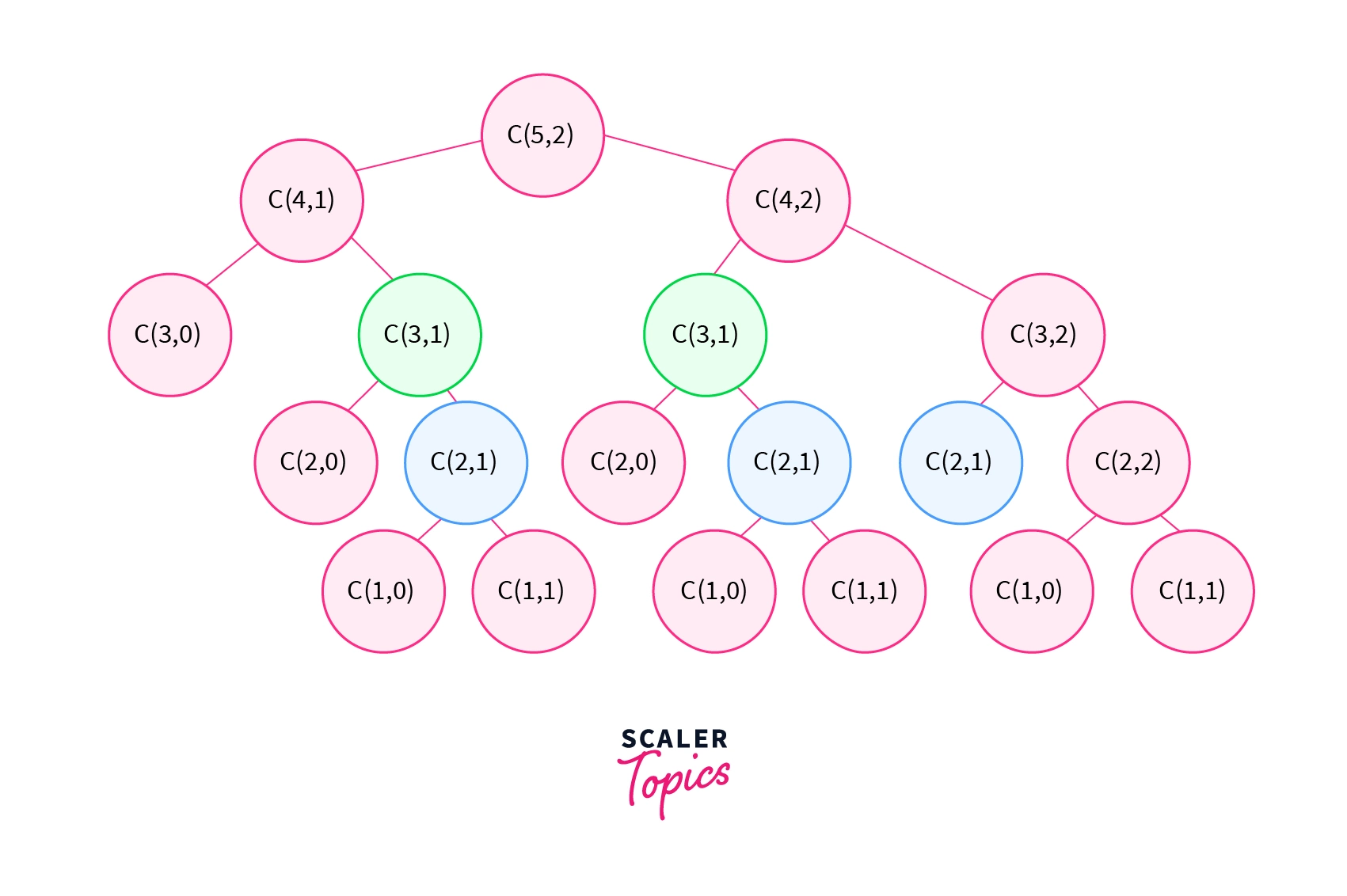
Recomputations of the same problem are avoided in Dynamic Programming by employing a 2D array in a bottom-up fashion. However, the time and space complexity does not differ significantly in either situation.

If you were to write a function for the same purpose, you would write it like follows:

int binCoeffDP(int n, int k)
{
    int C[n + 1][k + 1];
    int i, j;


    for (i = 0; i <= n; i++) {
        for (j = 0; j <= min(i, k); j++) {
            if (j == 0 || j == i)
                C[i][j] = 1;
            else
                C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
        }
    }

    return C[n][k];
}
int min(int a, int b) { return (a < b) ? a : b; }

Here,
Time Complexity: O(n* k)
Space Complexity: O(n* k)

Improving the initial solution by reducing the state space

We may use a 1D array instead of a 2D array to further limit the auxiliary space. This dimension reduction allows us to shrink the state space by a whole dimension.

A Pascal triangle can be used to implement a 1D array to solve this. Consider an i-row pascal triangle. Each row builds on the one before it, i.e. the (i-1)th row.

C[i]=C[i]+C[i-1]

The calculation in this scenario takes place as follows:

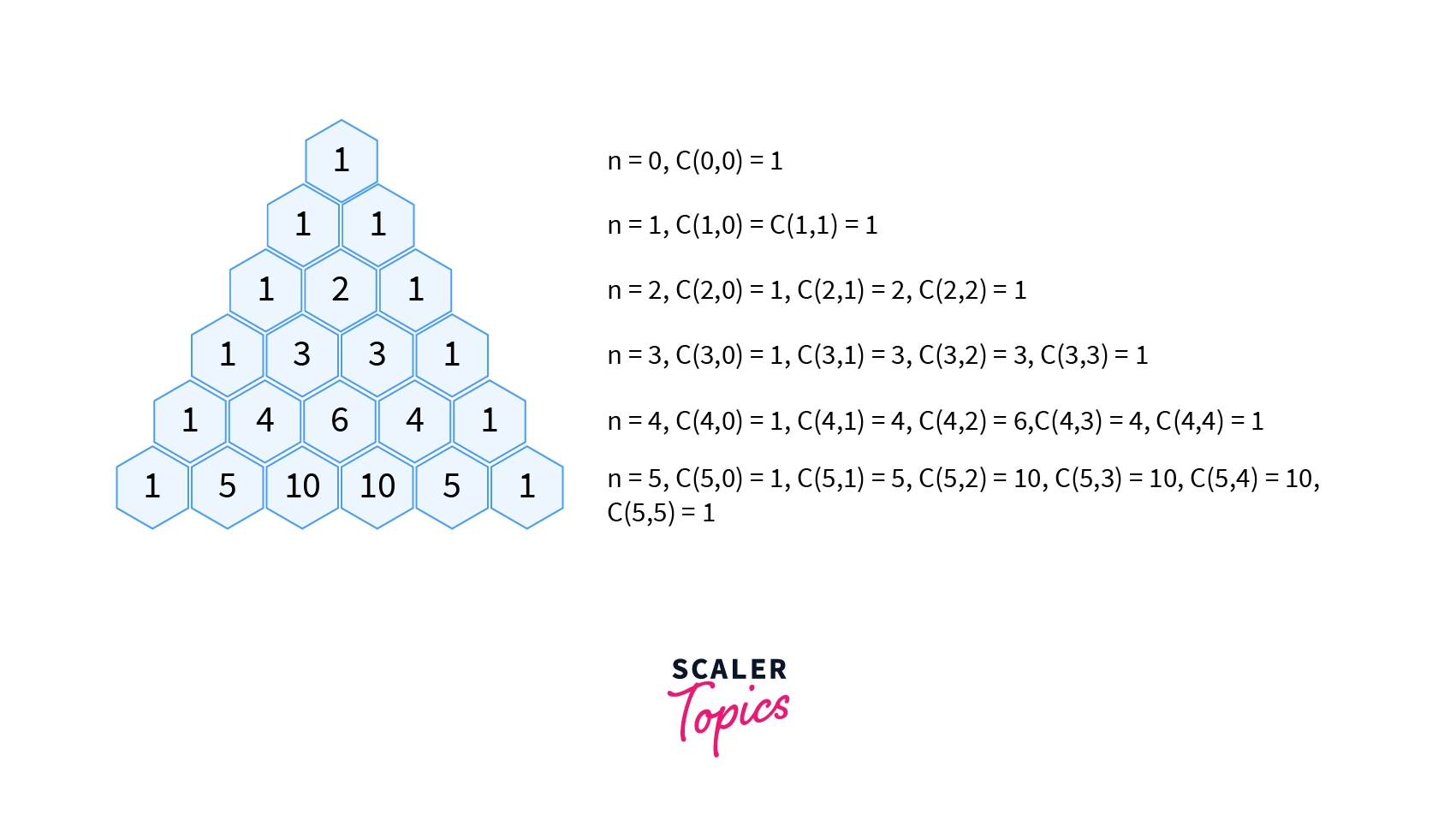
The right-hand side indicates the value from the previous iteration (each row of Pascal’s triangle is dependent on the row before it). The value of the current iteration obtained by this statement is represented on the left-hand side.

Let’s say we want to calculate C(3, 2),
i.e. n=3, k=2:

All elements of array C are
initialized to ZERO.

i.e. C[0] = C[1] = C[2] = C[3] = C[4] = 0;
Then C[0] is set to 1

For i = 1:
C[1] = C[1] + C[0] = 0 + 1 = 1 ==>> C(1,1) = 1

For i = 2:
C[2] = C[2] + C[1] = 0 + 1 = 1 ==>> C(2,2) = 1
C[1] = C[1] + C[0] = 1 + 1 = 2 ==>> C(2,1) = 2

For i=3:
C[3] = C[3] + C[2] = 0 + 1 = 1 ==>> C(3,3) = 1
C[2] = C[2] + C[1] = 1 + 2 = 3 ==>> C(3,2) = 3

C(3,2) = 2 is the answer.

To implement the above solution, consider the following code:

int binCoeffPasc(int n, int k)
{
    int C[k + 1];
    memset(C, 0, sizeof(C));

    C[0] = 1; // nC0 is 1

    for (int i = 1; i <= n; i++)
    {
        for (int j = min(i, k); j > 0; j--)
            C[j] = C[j] + C[j - 1];
    }
    return C[k];
}

Here,
Time Complexity: O(n * k)
Space Complexity: O(k)

This is simply one solution to the problem. There are other more approaches inside dynamic programming that can assist us in achieving the best possible result.

Conclusion

• The primary principle of dynamic Programming is to prevent repetitive effort by remembering partial outcomes, and this approach is used in a variety of real-world scenarios.
• The complexity of dynamic programming is reduced by reducing state space.
• There are various methods for limiting the number of states in a dynamic programming solution, but none is universal.
• The most popular method is to try to reduce the size of one of the existing dimensions. When the size is reduced by a factor of, the overall time complexity of the solution remains the same, but the constant factor improves.