A spanning tree in data structures is a sub-graph, that contains all the vertices of a graph. A spanning tree may or may not be weighted, a spanning tree does not have cycles and it cannot be disconnected. The spanning tree has a minimal set of edges. A single connected graph can have multiple spanning trees.
Graph
A graph can be depicted as a set of vertices connected by edges. The most common types of graphs are as follows:
- Undirected Graph: This type of graph features bidirectional edges, meaning they don’t have a specified direction. It can be viewed as a graph with V vertices and E edges, where each edge connects two distinct vertices.
- Connected Graph: A connected graph is one in which there is always a path between any two vertices. Another way to express this is that a graph is connected if one can reach any vertex from any other vertex by following edges in either direction.
- Directed Graph: A graph is labeled as a directed graph if all the edges between nodes or vertices have a specified direction.
What is Spanning Tree?
A spanning tree is a sub-graph that connects all the vertices of the graph with the minimum possible number of edges. Spanning Trees of a given graph G can also be defined as a minimal set of edges that contains all the vertices of G. A spanning tree does not have any cycle and it can never be disconnected. A spanning tree can be weighted or unweighted.
Example of Spanning Tree
A complete undirected graph G can have a maximum nn-2 number of spanning trees, where n is the number of nodes in a given graph G. Let us Consider a complete graph G with 3 vertices, then the total number of spanning trees this graph can have is 3(3-2)=3 which are shown in the image below.
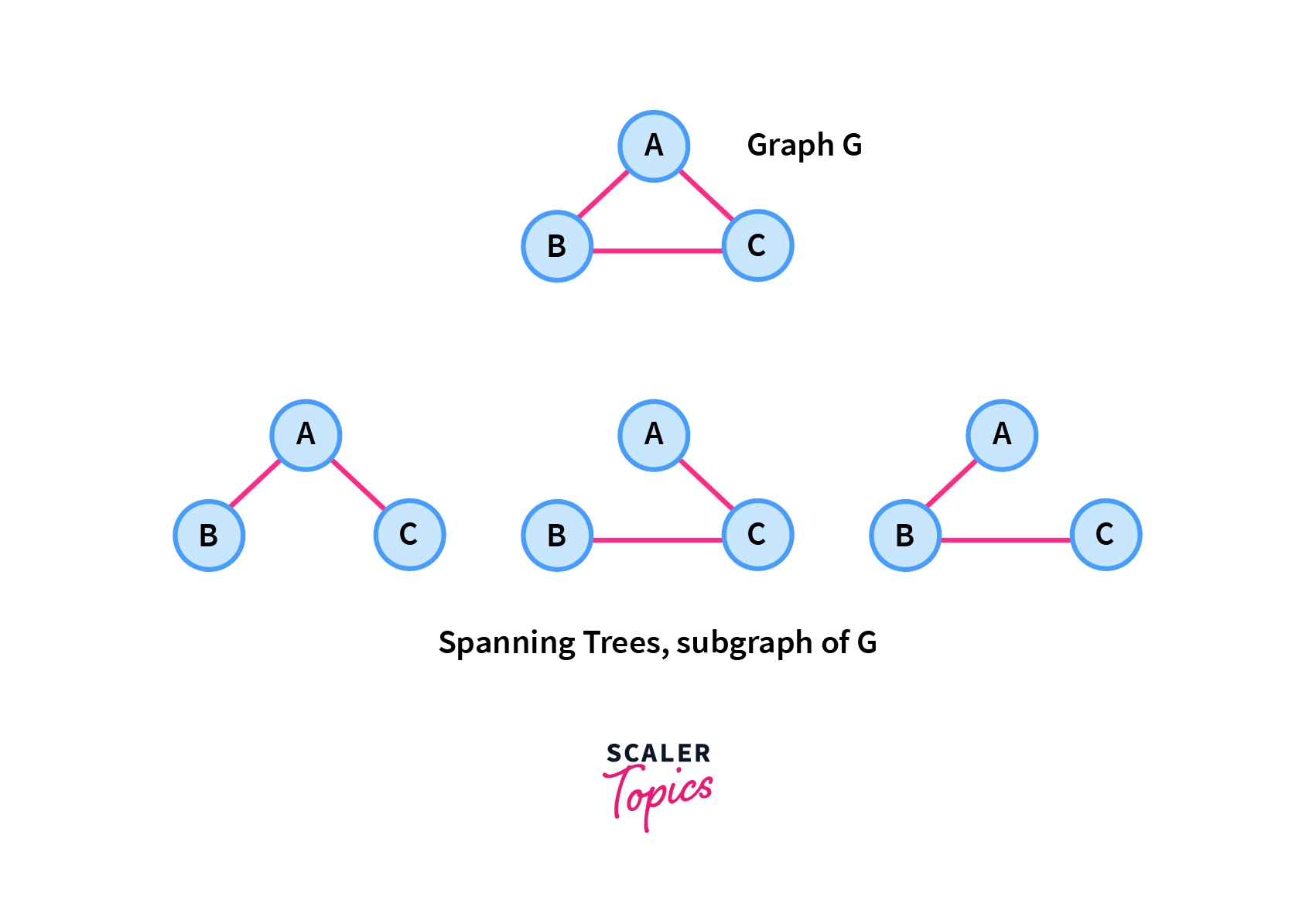
In the above picture, we can see that the tree have no cycles and they are minimally connected so they are all the possible spanning trees of 3 vertices for a given graph G.
Properties of Spanning Tree
Let us discuss some properties of a spanning tree.
- All possible spanning trees for graph G have the same number of edges and vertices.
- Spanning trees do not have any cycles.
- A spanning tree is a minimally connected sub-graph, which means if we remove any edge from the spanning tree then it becomes disconnected.
- A spanning tree is a maximally acyclic sub-graph, which means if we add an edge to the spanning tree then it becomes cyclic.
- A connected graph G can have more than one spanning tree.
- A disconnected graph cannot have a spanning tree.
- In the case of a connected graph with N vertices, the number of edges in its spanning tree is equal to N-1.
- To construct a spanning tree for a complete graph, remove E-N+1 edges, where E is the number of edges, and N is the number of vertices.
- Cayley’s Formula states that the total number of spanning trees that a complete graph of n vertices can have is n(n-2).
Applications of Spanning Tree
Following are a few applications of spanning trees:
- Computer Networking: Spanning trees, especially through protocols like the Spanning Tree Protocol (STP), play a crucial role in optimizing and organizing networks. They ensure efficient data travel without causing loops.
- Electrical Power Systems: Spanning trees assist in identifying the minimum spanning tree, optimizing the distribution of power lines to minimize costs and energy loss.
- Geographic Information Systems (GIS): Spanning trees are used in GIS to design efficient transportation networks, determining the most economical routes for connecting different locations.
- Biology: Spanning trees are employed in biology to model hierarchical structures, such as phylogenetic trees, representing evolutionary relationships among species.
What is Minimum Spanning Tree?
A minimum spanning tree is the spanning tree that has a minimum cost among all the spanning trees. The cost of the spanning tree is the sum of the weights of all the edges in the tree. In real-life situations, this weight can be measured as distance, cost of transportation, manufacturing cost, traffic load, or any arbitrary value denoted by the edges. A minimum spanning tree has (V – 1) edges where V is the number of vertices in the given graph.
For a given graph G, a minimum spanning tree of a graph is unique if the weight of all the edges is distinct. Otherwise, there may be multiple possible minimum spanning trees.
Example of Minimum Spanning Tree
Let us understand the Minimum Spanning Tree with the help of the example below.
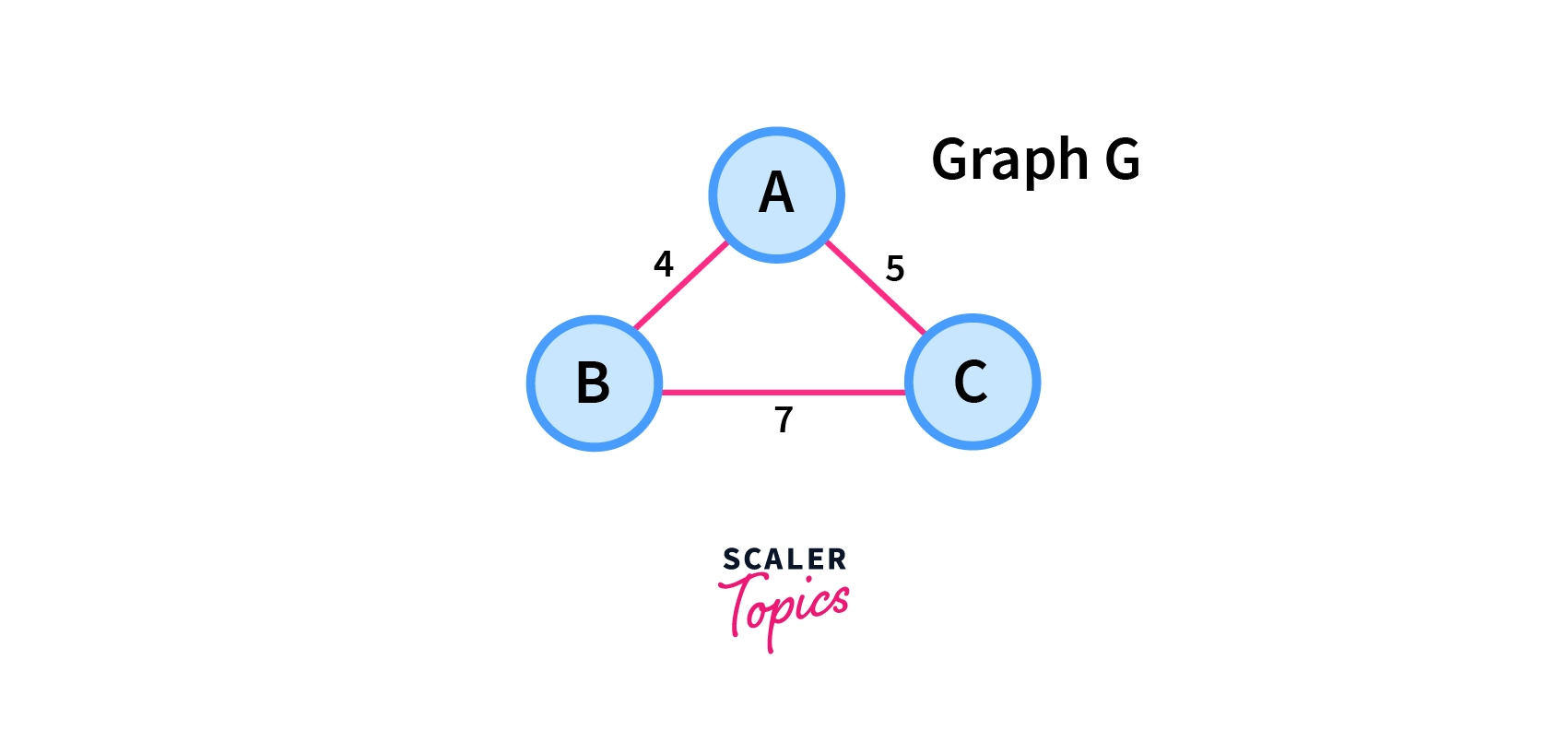
Now let us see some of the spanning trees which are possible with this graph G.
1.
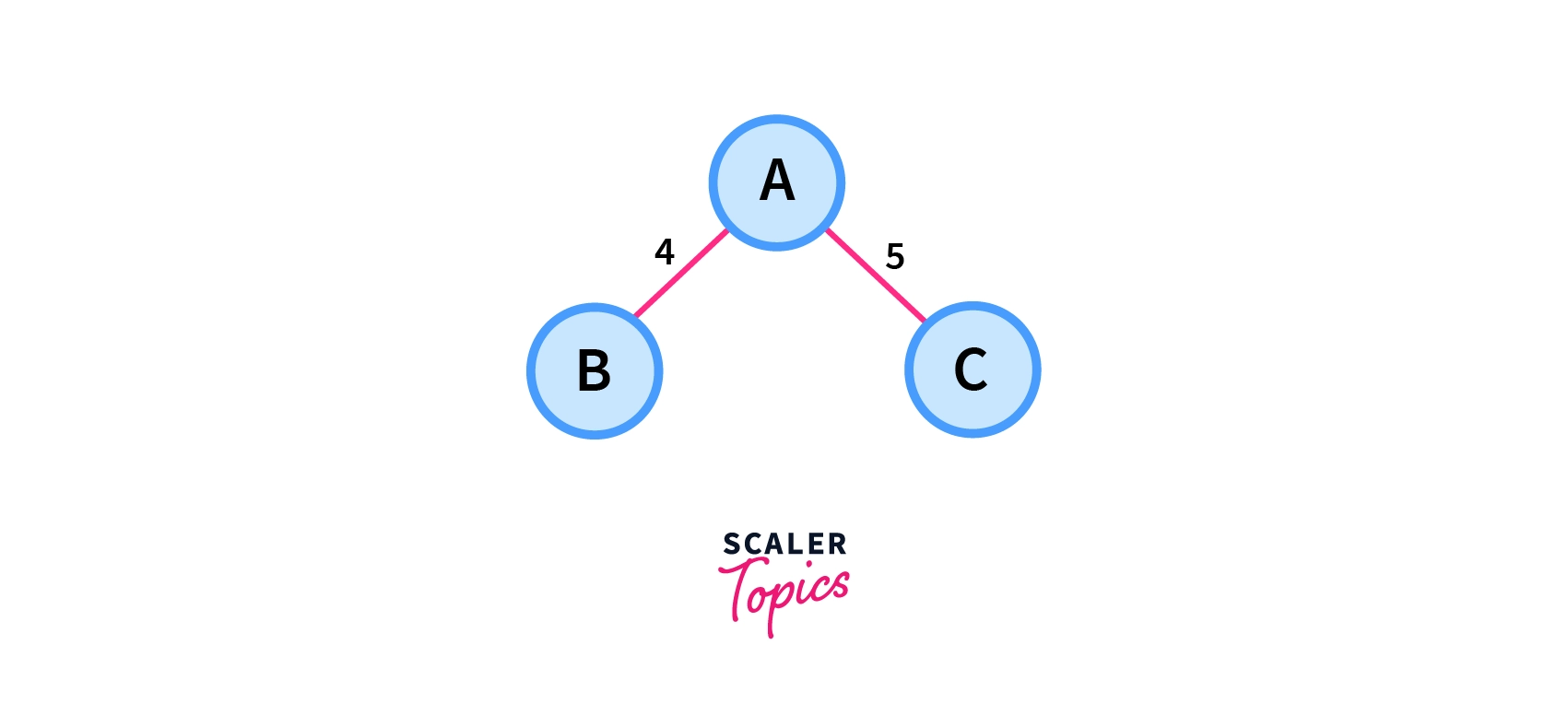
Total Cost=4+5=9
2.
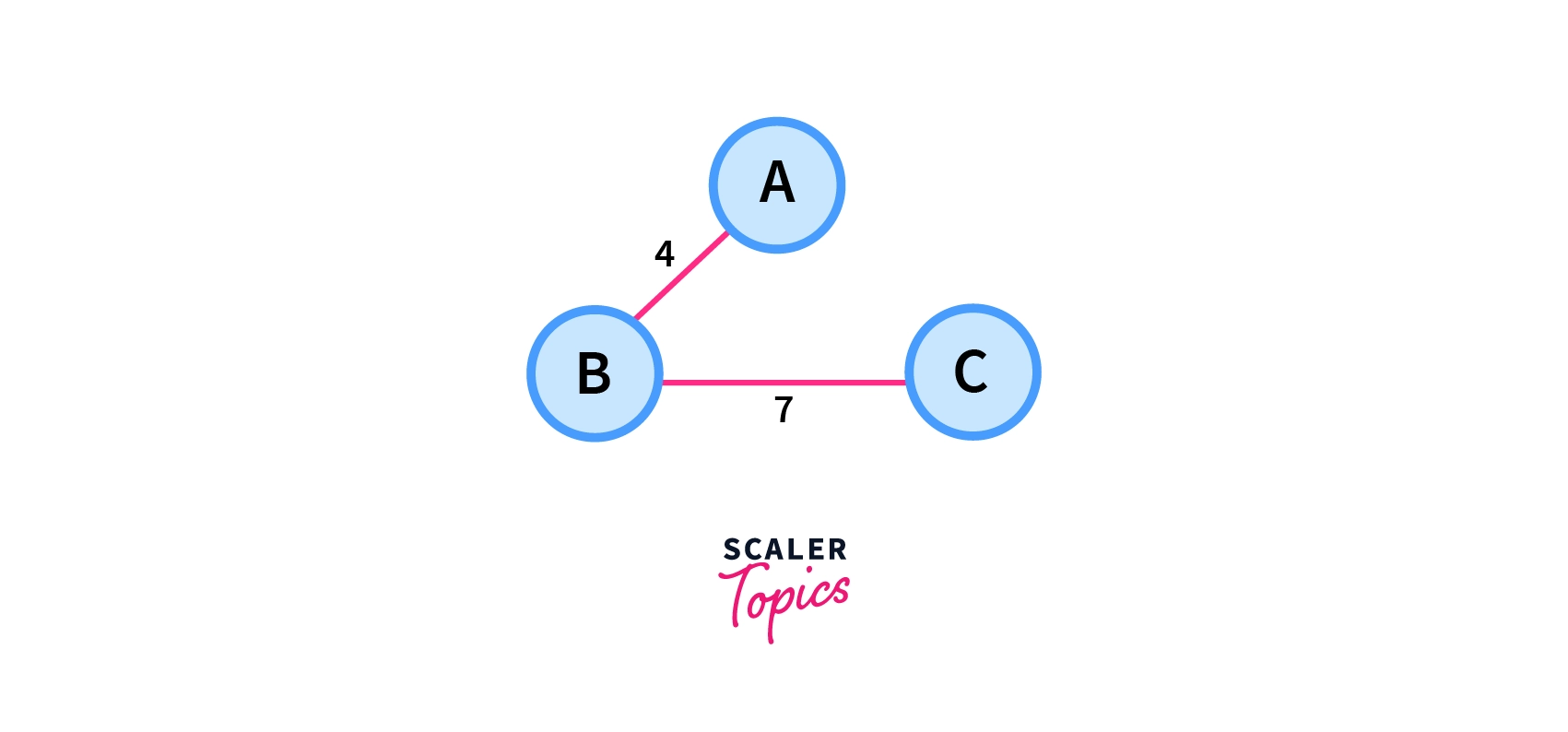
Total Cost=4+7=11
3.
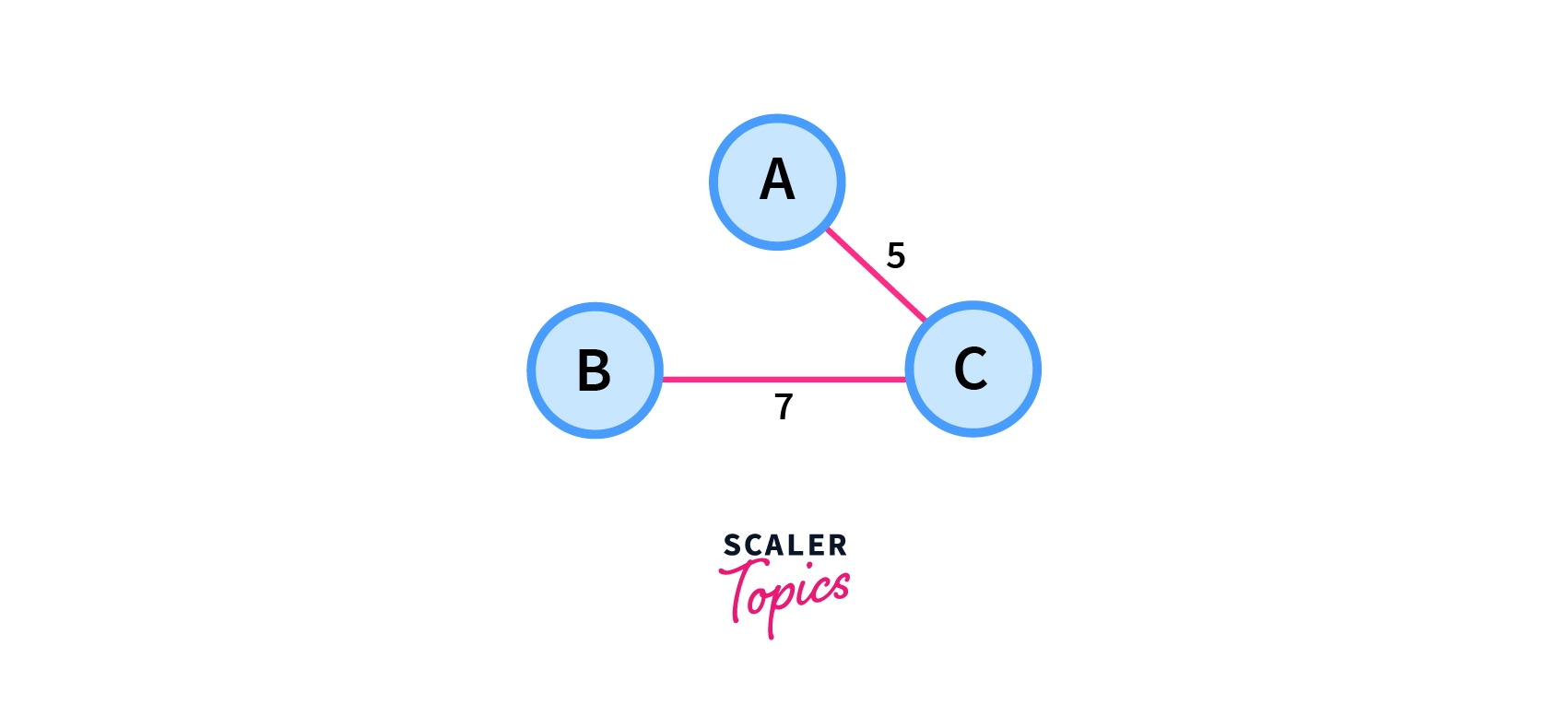
Total Cost=7+5=12
From the above three cases, we can see that among all possible spanning trees figure 1 has the minimum cost, So it is the minimum spanning tree among the given spanning trees.
Properties of Minimum Spanning Tree
Let us discuss some properties of a minimum spanning tree.
- A minimum spanning tree connects all vertices in the graph, providing a path between any pair of nodes.
- An MST is acyclic, ensuring it remains a tree without cycles or loops.
- An MST with
Vvertices (whereVis the number of vertices in the original graph) will have exactlyV – 1edges. - While optimal for minimizing total edge weight, an MST may not be unique.
- The cut property asserts that, for any cut in the original graph (a partition of vertices into two sets), the minimum-weight edge crossing the cut is part of the MST.
Applications of Minimum Spanning Tree
Following are the applications of MSTs:
- Network Design: MSTs contribute to the optimization and efficiency of communication infrastructure in network design. They help establish the most cost-effective and reliable network of cables, particularly in telecommunications, for efficient data transmission.
- Logistics and Transportation Planning: MSTs are utilized in logistics and transportation planning to design the most economical routes for delivery and distribution, thereby minimizing overall costs.
- Circuit Design and Wiring Layout: In circuit design and wiring layout, MSTs assist in minimizing the total length of wires, leading to reduced material and operational expenses.
Minimum Spanning Tree Algorithm
There are two famous algorithms for finding the Minimum Spanning Tree of a graph:
Kruskal’s Algorithm
In Kruskal’s Algorithm, the spanning tree is constructed by adding the edges one by one. Kruskal’s Algorithm is based on the greedy approach because every time we add that edge that has the least weight among all available options.
Algorithm Steps:
- Sort all the edges of the graph in the increasing order of their weight.
- Pick the edge with the smallest weight.
- Check if it forms a cycle with the spanning tree formed so far.
- Include the current edge if it does not form any cycle.
- Otherwise discard it.
- Repeat step
3until thereV-1edges in the spanning tree, where V is the total number of vertices in the graph.
The Kruskal’s algorithm is a Greedy Algorithm. The greedy choice is to pick the smallest weight edge that does not cause a cycle in the MST constructed so far.
To detect if after including the current edge it will form a cycle or not we use the union finds algorithm.
Example
Let us understand the working of Kruskal’s Algorithm with an example.
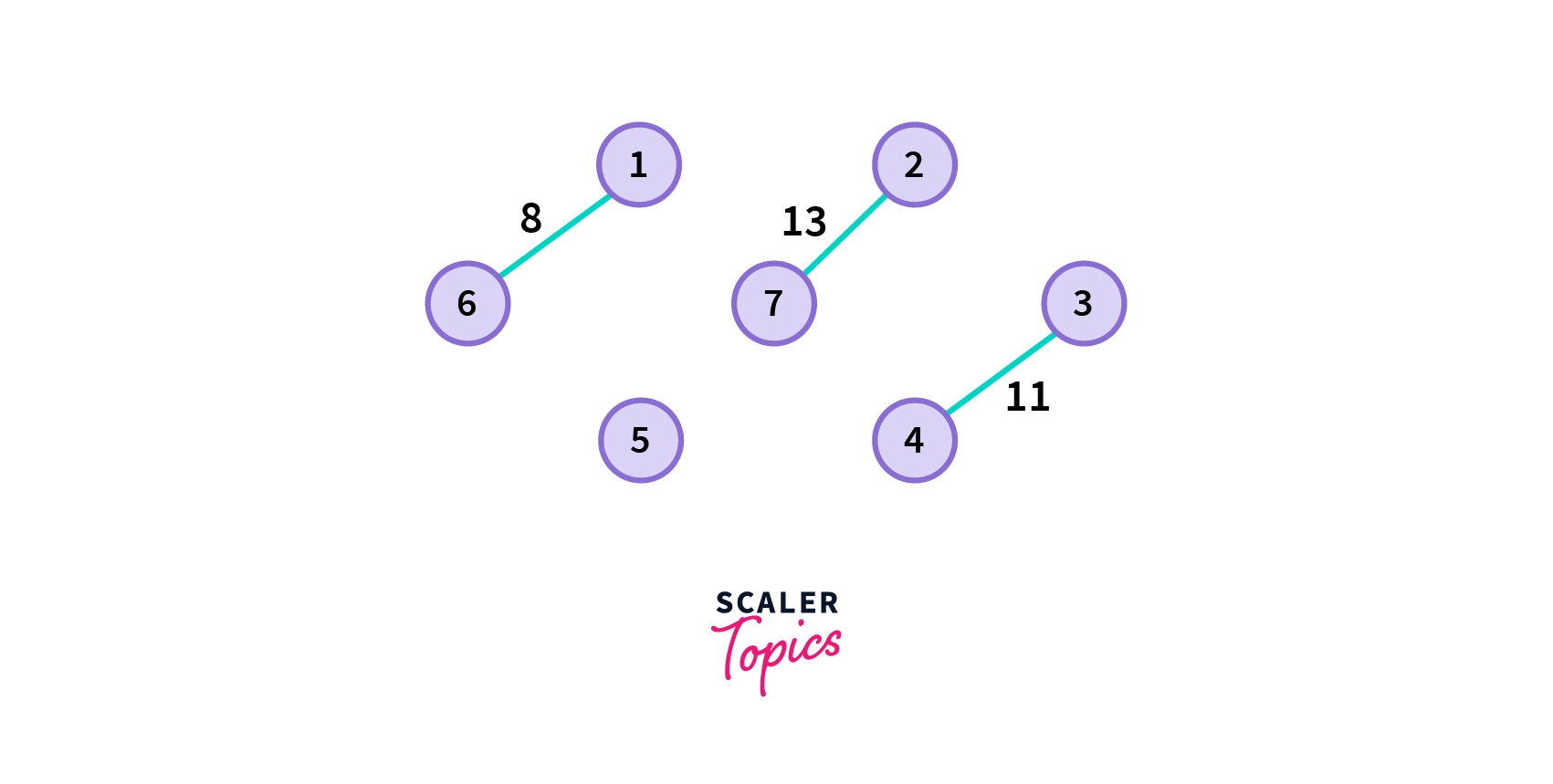
Consider a weighted graph G having seven vertices in the picture below.
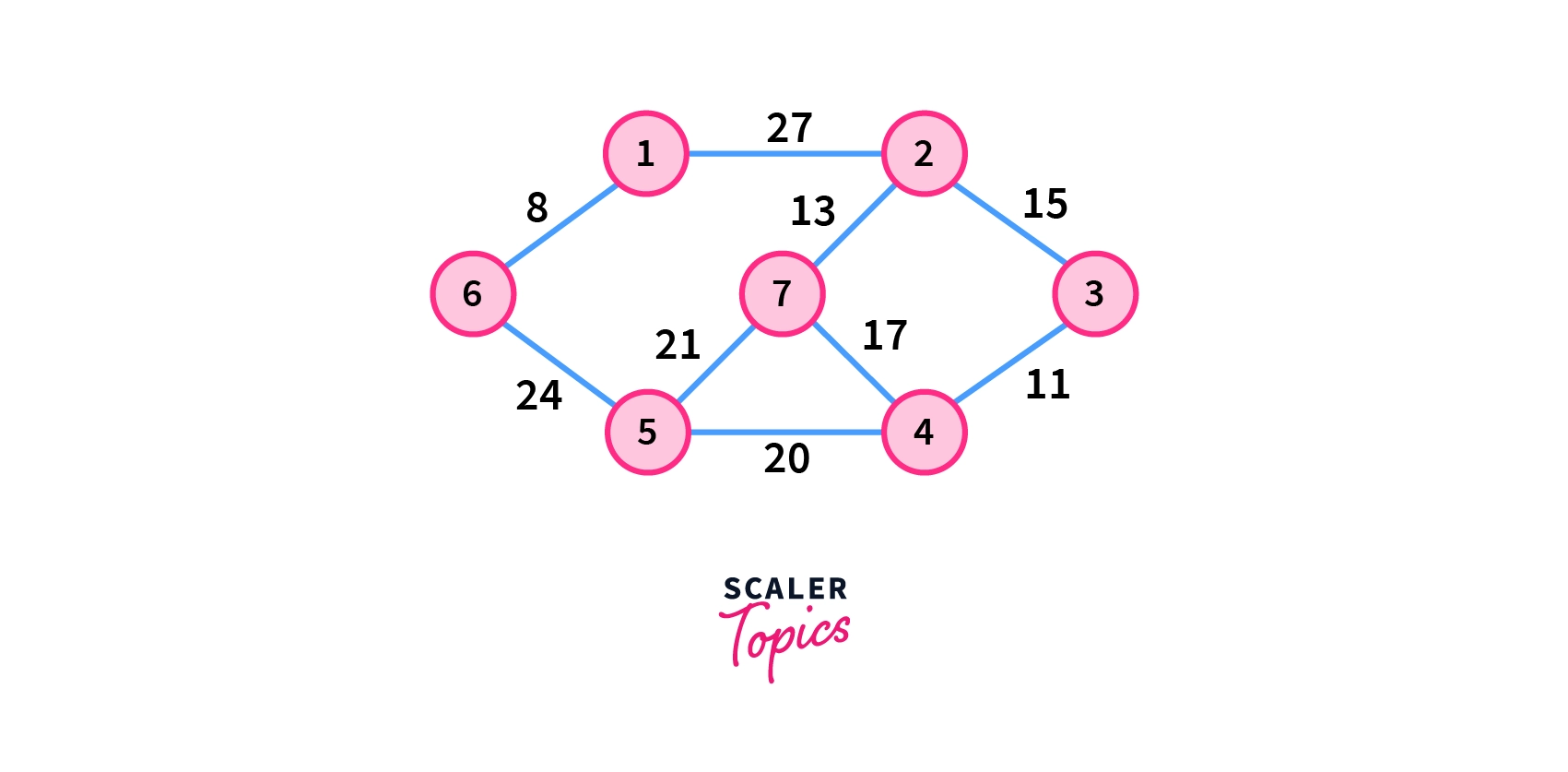
Now to find the minimum spanning tree using Kruskal’s Algorithm, follow the steps below.
- Choose the edge with the minimum weight.
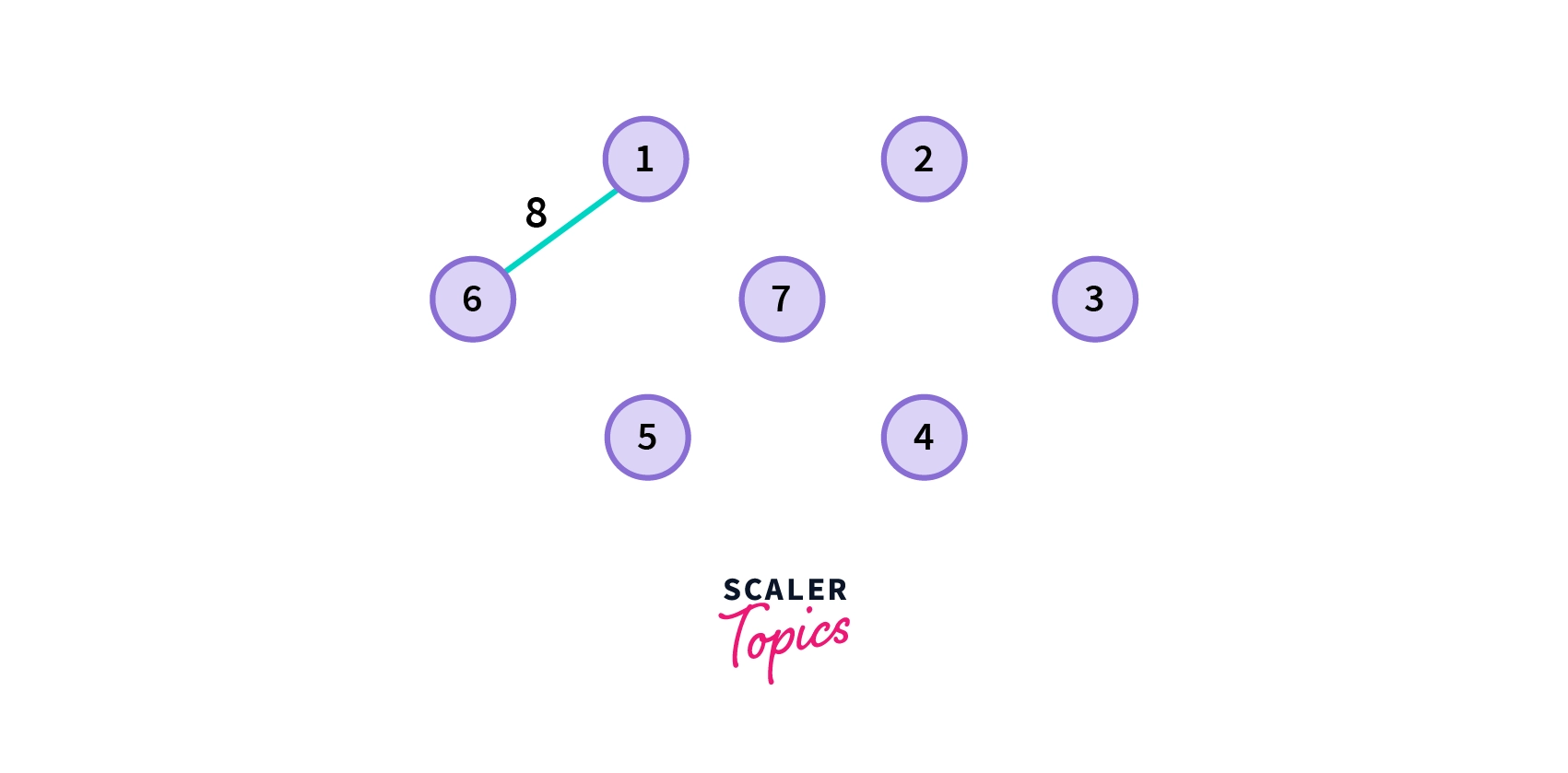
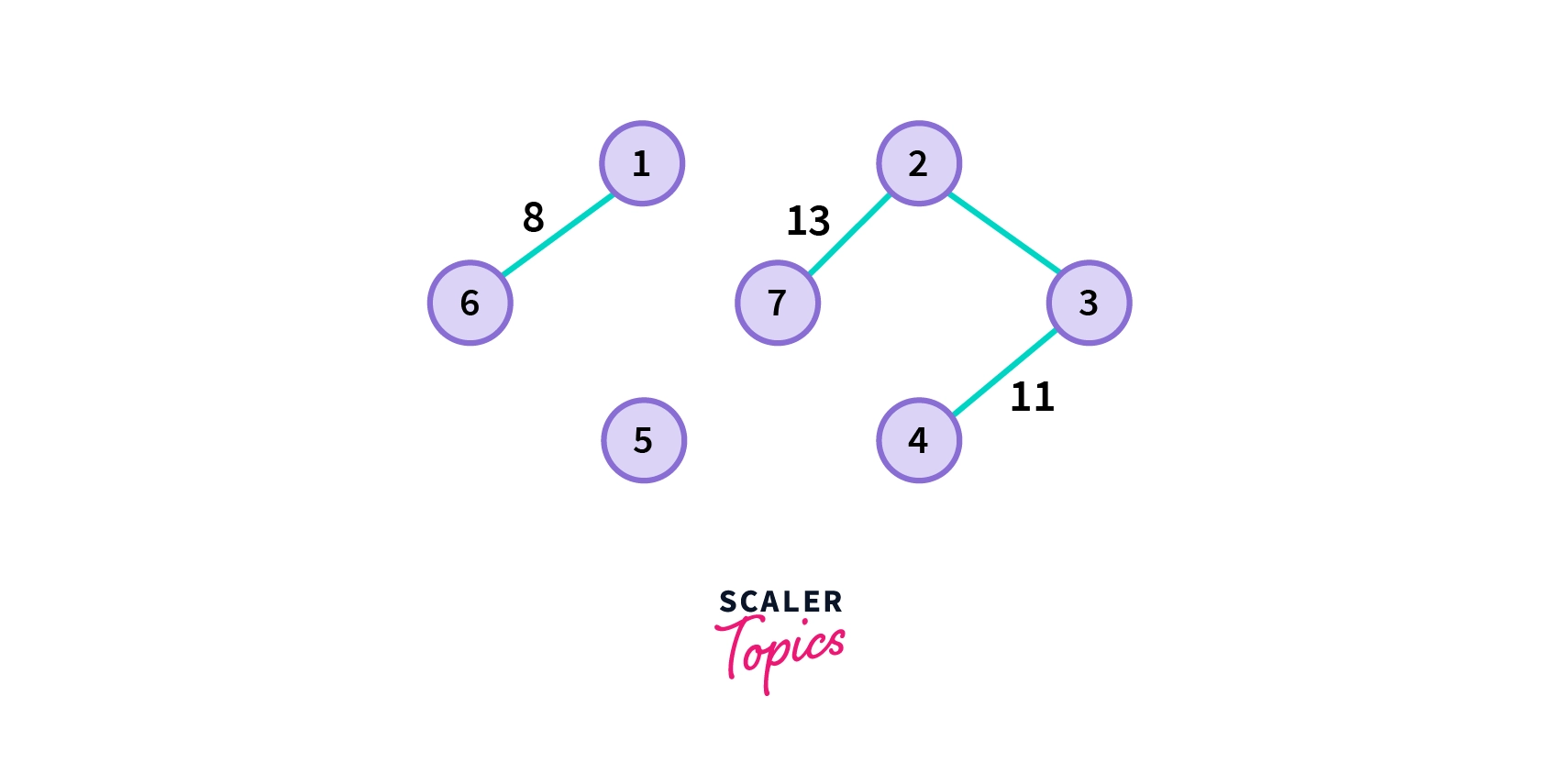
2. Choose the next shortest edge and add it. We can see from the picture below that the next shortest edge cannot be connected to the former one.
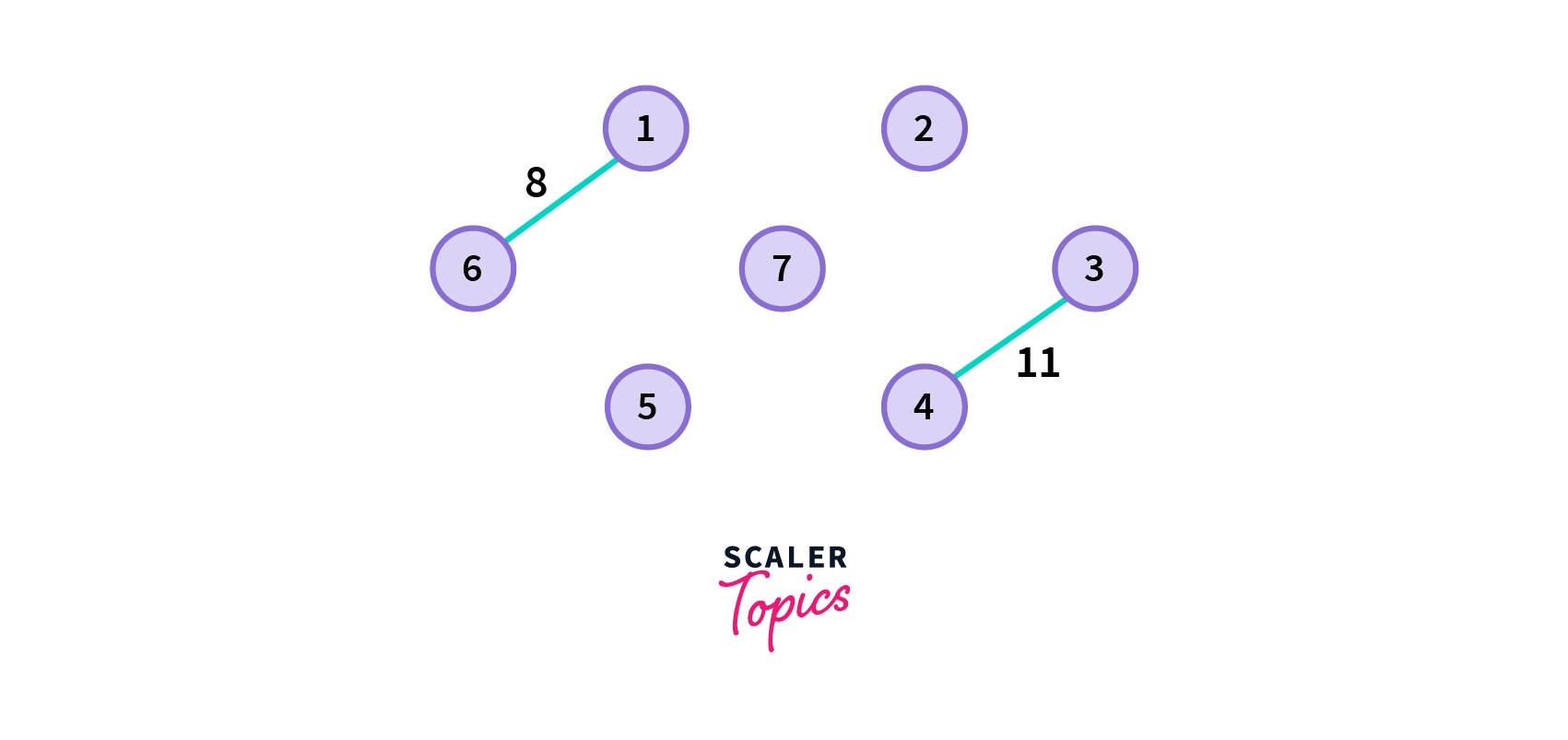
- Choose the next shortest edge that doesn’t create a cycle and add it.
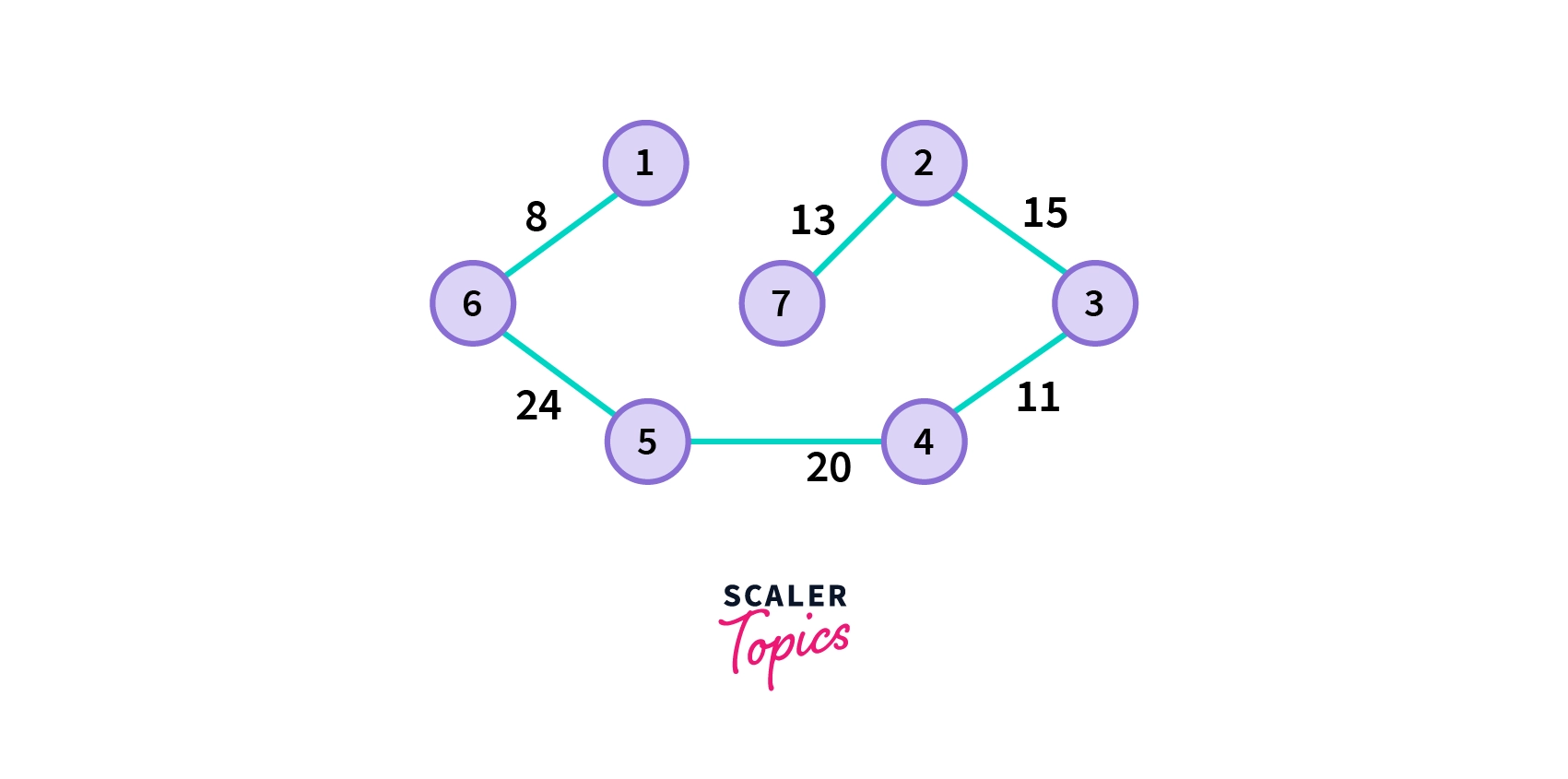
- Choose the next shortest edge that doesn’t create a cycle and add it. If there are more than one such edges, choose anyone from them.
- Choose the next shortest edge that doesn’t create a cycle and add it.

- Repeat step
5until you a spanning tree.
Here is the C++ implementation of the above approach
#include <bits/stdc++.h>
using namespace std;
// Edge class to represent the Graph
class Edge
{
public:
int source;
int dest;
int weight;
};
// Utility function to sort all the edges in the increasing order of their weights.
bool compare(Edge e1,Edge e2)
{
return e1.weight<e2.weight;
}
// Function to find the parent of given vertex
int Find_Parent(int x,int *parent)
{
if (parent[x]==x)
return x;
return Find_Parent(parent[x],parent);
}
// Function to implement the Kruskal's Algorithm
void Kruskals_MST(Edge *input,int V,int E)
{
//Sort the Edges in the increasing order of their weights
sort(input,input+E,compare);
// output array to represent the Minimum Spanning Tree
Edge *output=new Edge[V-1];
// Create parent array to Store the parent of each Vertex
int *parent=new int[V];
// Make Every Vertex parent of itself.
for (int i=0;i<V;i++)
parent[i]=i;
int count=0;
int i=0;
while(count!=V-1)
{
Edge curr_edge=input[i];
// Find the Source and Destination of the Current Edge
int Source_Parent=Find_Parent(curr_edge.source,parent);
int Dest_Parent=Find_Parent(curr_edge.dest,parent);
// If Source Parent is not equal to the Destination Parent
// then adding the Current Edge will not form any Cycle.
if (Source_Parent!=Dest_Parent)
{
output[count]=curr_edge;
count++;
parent[Source_Parent]=Dest_Parent;
}
i++;
}
//Print the Minimum Spanning Tree
cout<<"Source"<<' '<<"Destination"<<' '<<"Weight"<<endl;
for (int i=0;i<V-1;i++)
{
if (output[i].source<output[i].dest)
{
cout<<output[i].source<<"\t\t"<<output[i].dest<<"\t\t\t"<<output[i].weight<<endl;
}
else
{
cout<<output[i].dest<<"\t\t"<<output[i].source<<"\t\t\t"<<output[i].weight<<endl;
}
}
}
int main() {
int V,E;
cin>>V>>E;
// Create input array to store all the Edges of the Graph.
Edge *input=new Edge[E];
int s,d,w;
for (int i=0;i<E;i++)
{
cin>>s>>d>>w;
input[i].source=s;
input[i].dest=d;
input[i].weight=w;
}
Kruskals_MST(input,V,E);
return 0;
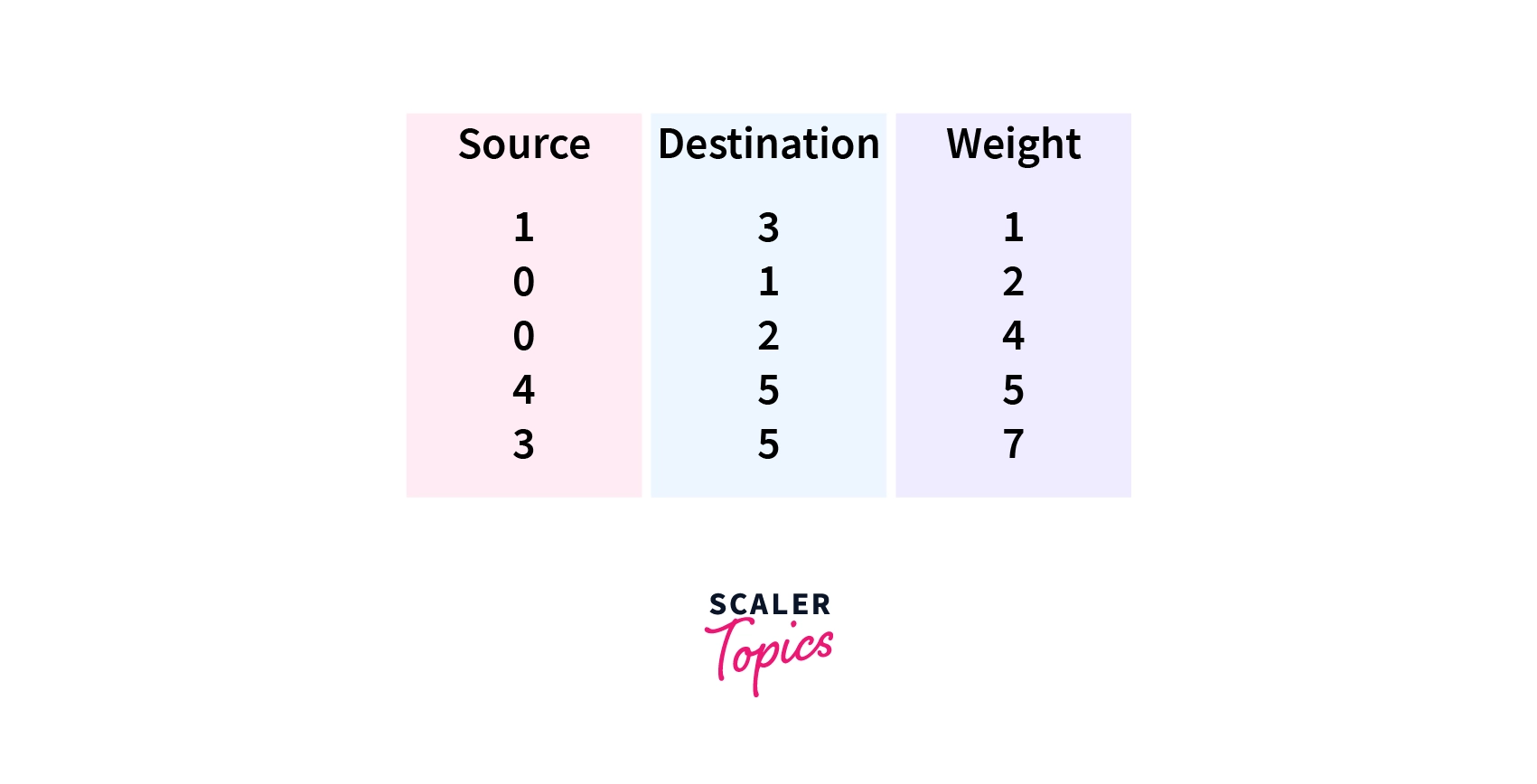
}Input of Above Code
6 11
0 1 2
1 3 1
0 2 4
2 4 9
4 5 5
3 5 7
4 3 11
2 5 10
0 3 3
2 1 8
2 3 6Output of Above Code
Prim’s Algorithm
Like Kruskal’s Algorithm the Prim's Algorithm is also used to find the minimum spanning tree from a graph. In Prim’s algorithm, we find the subset of edges that includes every vertex of the graph in such a manner that the sum of the weights of the edges can be minimized. Unlike Kruskal's algorithm, Prim's algorithm treats the nodes as a single tree and keeps on adding new nodes to the spanning tree from the given graph.
Algorithm Steps:
- Initialize:
- Select an arbitrary starting vertex.
- Create an empty set to keep track of selected vertices, initially containing only the starting vertex.
- Create a priority queue (or Min Heap) to store the edges and their weights.
- Repeat until all vertices are included:
- Select the Minimum Weight Edge:
- Iterate through all the edges connected to the currently selected vertices.
- Add all the edges connecting a selected vertex to an unselected vertex to the priority queue.
- Choose the Minimum Weight Edge:
- Extract the edge with the minimum weight from the priority queue.
- Add the Vertex to the MST:
- Add the destination vertex of the selected edge to the set of selected vertices.
- Update the Priority Queue:
- Remove any edges in the priority queue that connect already selected vertices.
- Select the Minimum Weight Edge:
- Continue until the MST contains all vertices.
Example
Consider a weighted graph G having seven vertices in the picture below.
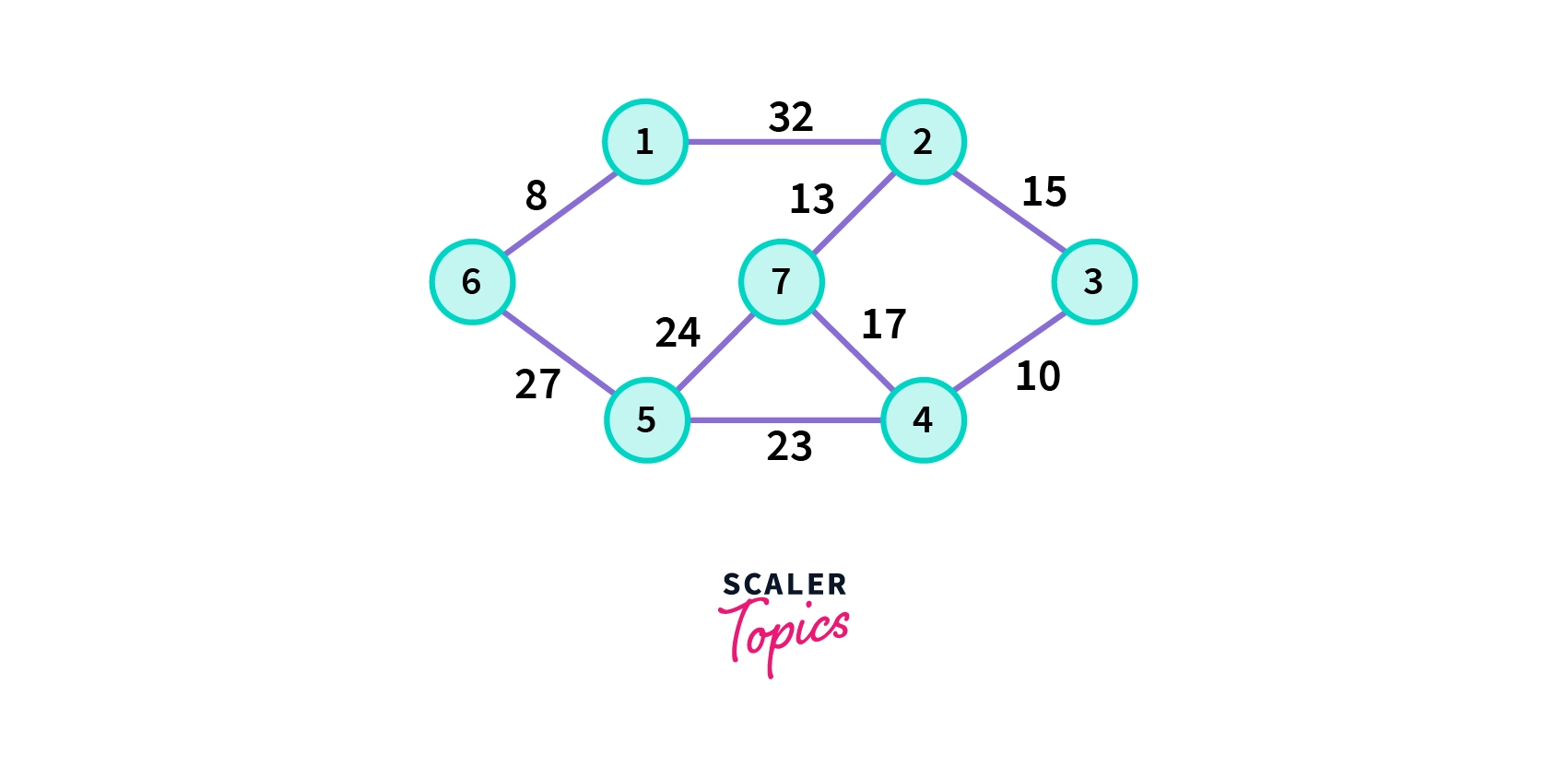
Now to find the minimum spanning tree using Prim’s Algorithm, follow the steps below.
1. Choose any arbitrary vertex , here we are starting from vertex 1 in the given graph G.
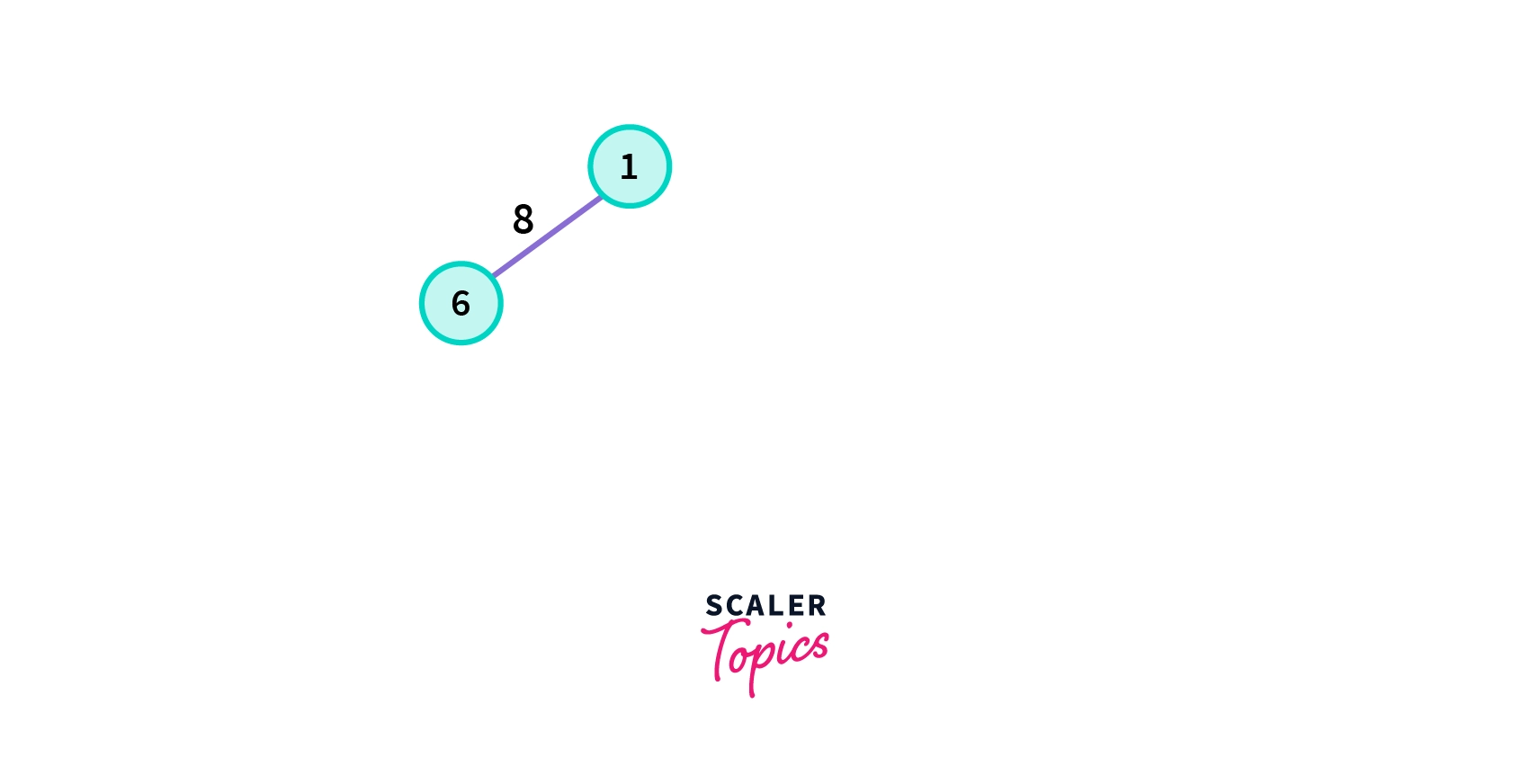
2. Choose the shortest edge from this vertex and add it to the spanning tree so formed.
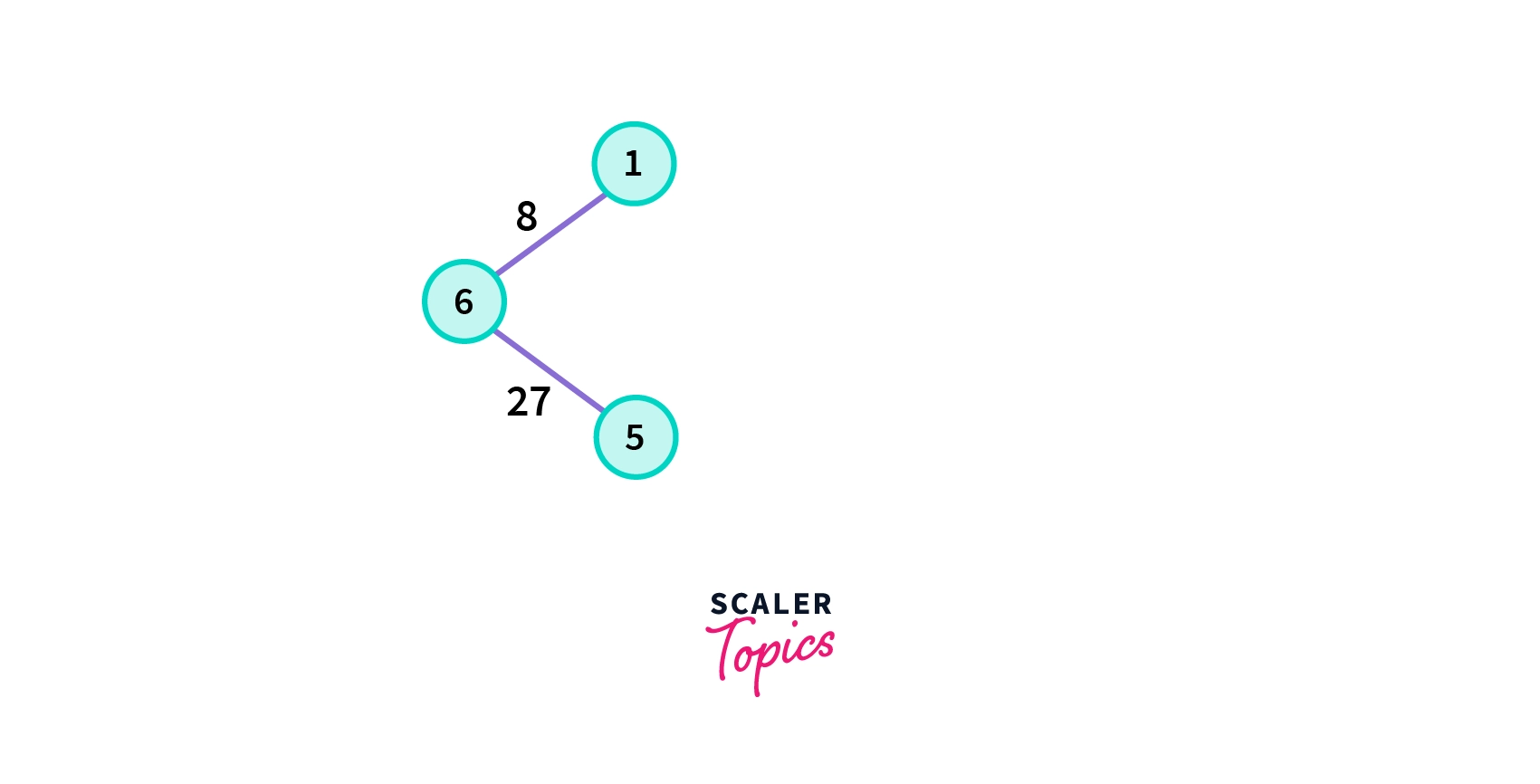
3. Choose the nearest vertex which is not yet included in the solution. In each iteration, we are considering all the respective fringe vertices for a particular vertex.
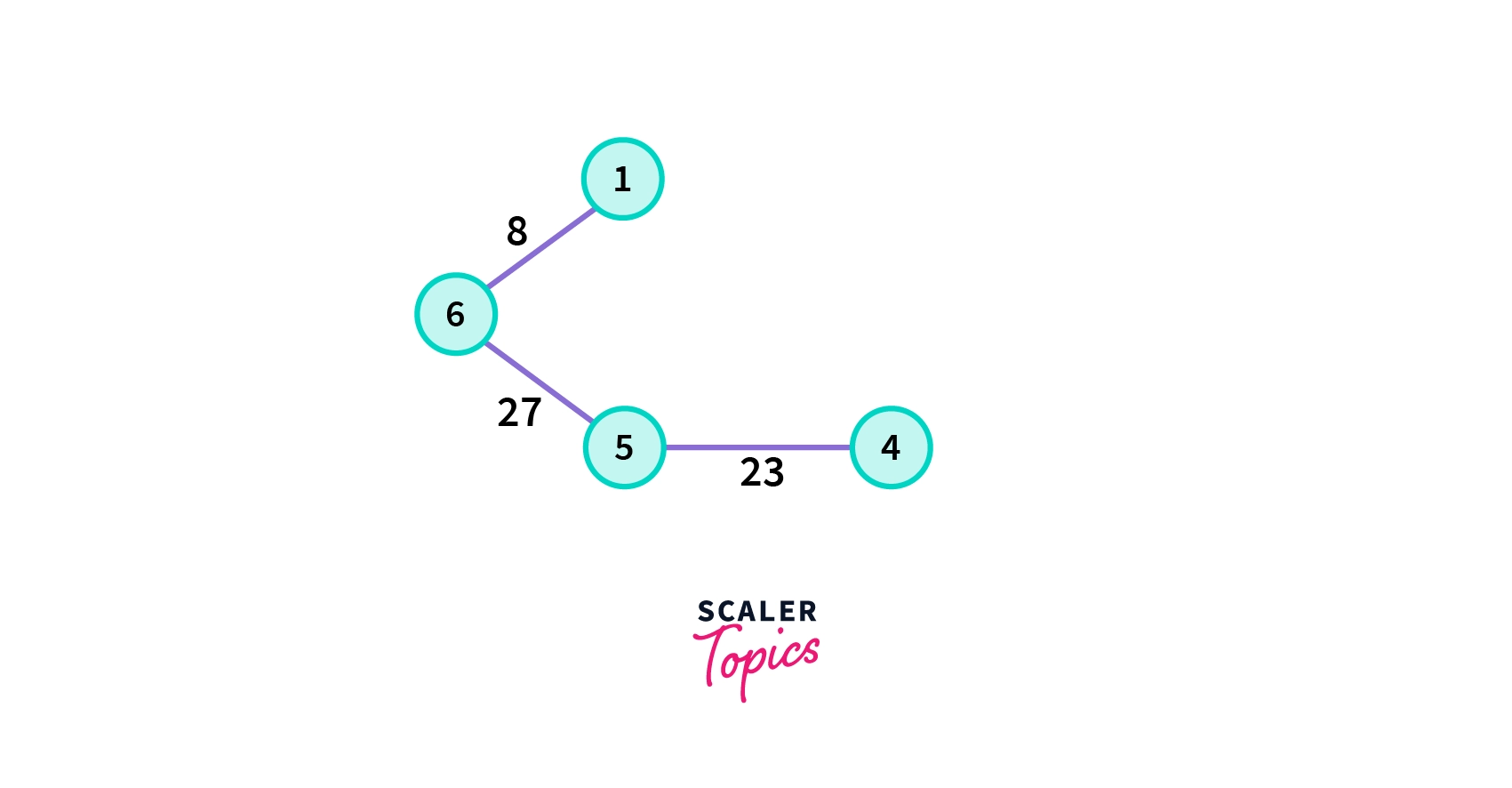
4. Choose the nearest vertex which is not yet included in the solution and does not form any cycle.
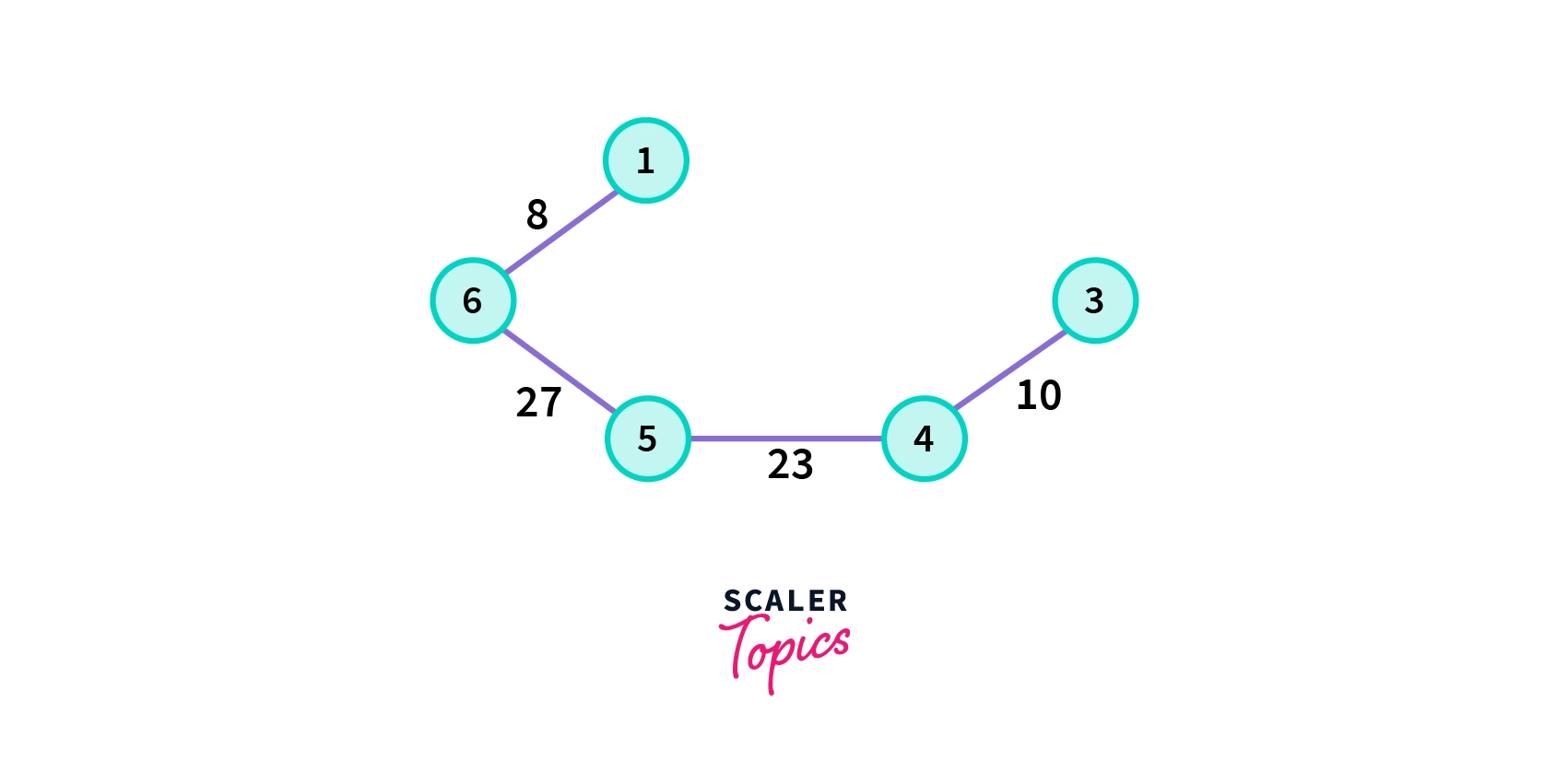
5. Choose the nearest vertex which is not yet included in the solution and does not form any cycle.
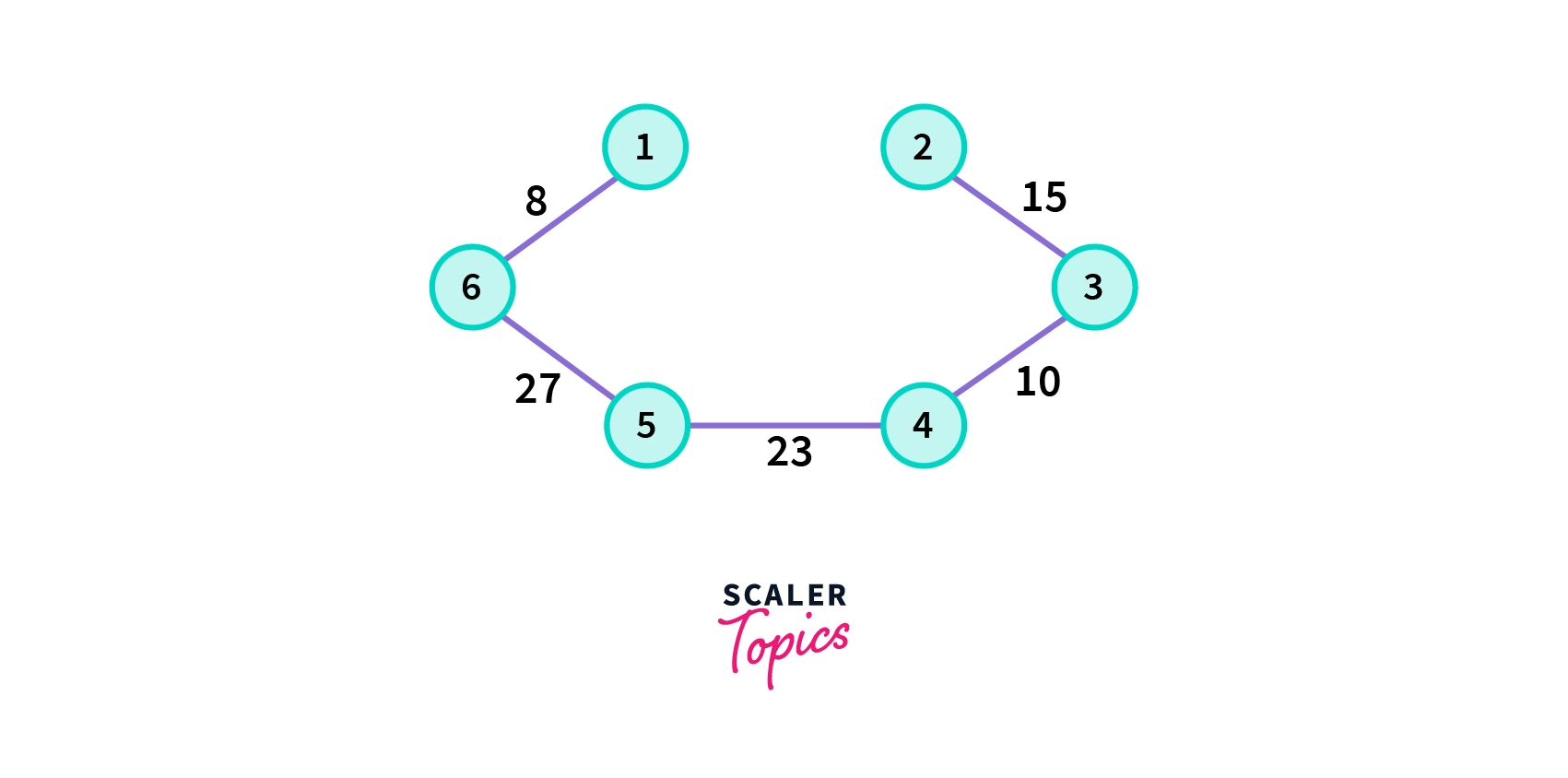
6. Repeat the same process until our minimum spanning tree does not have V-1 vertices, where v is the total number of vertices in the in original graph G.
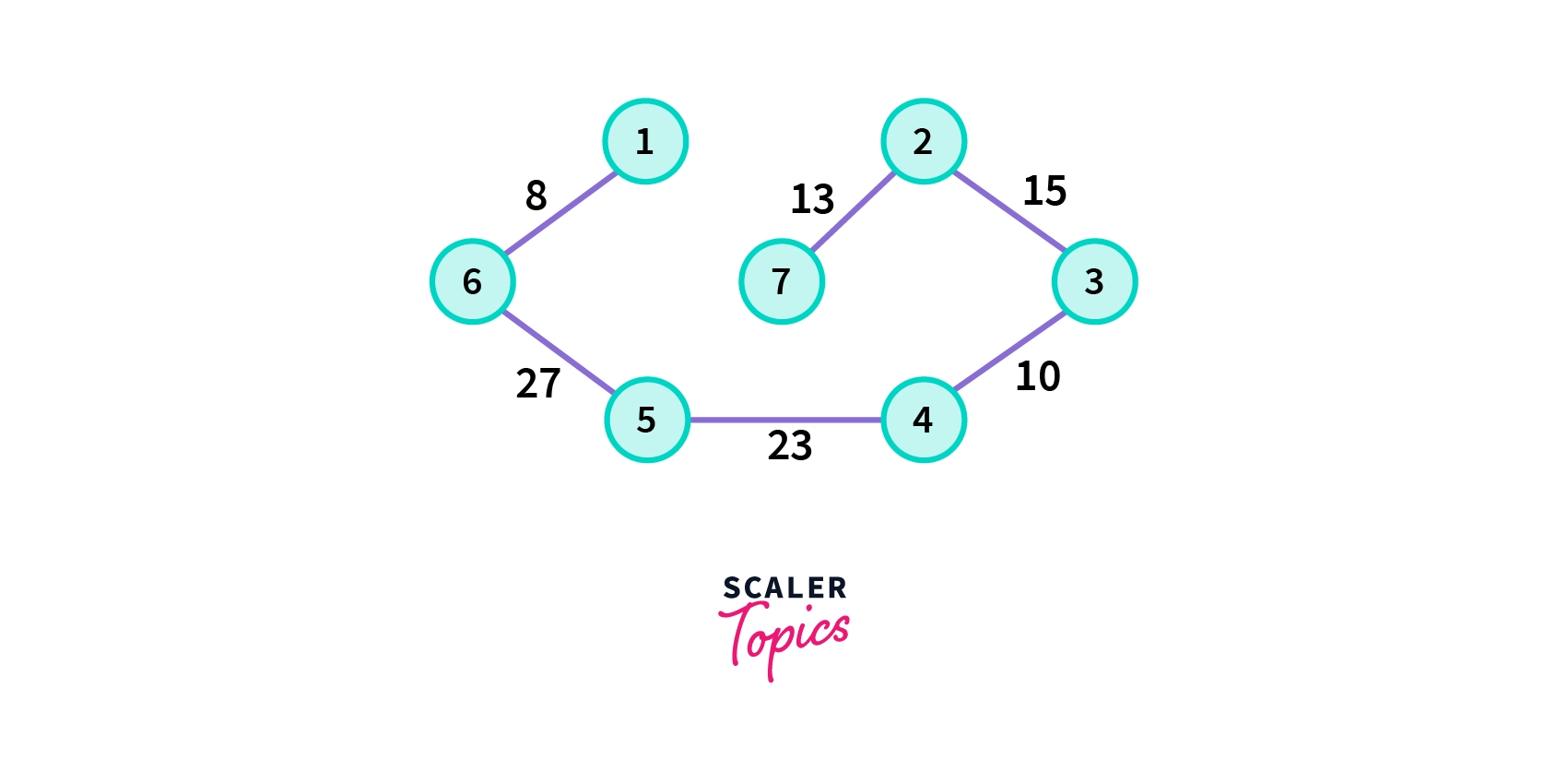
Here is the C++ implementation of the above approach
// Programe to implement the Prim's Algorithm using
// adjacency matrix representation of the graph
#include <bits/stdc++.h>
using namespace std;
// Number of vertices in the graph
#define V 5
// Function to find the vertex having the
// minimum key value, from the set of vertices
// which are not yet included in MST
int minKey(int key[], bool mstSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
// Function to print the
// constructed MST stored in parent[]
void printMST(int parent[], int graph[V][V])
{
cout<<"Edge \tWeight\n\n";
for (int i = 1; i < V; i++)
cout<<parent[i]<<" - "<<i<<" \t"<<graph[i][parent[i]]<<" \n";
}
// Function to construct and print MST for
// a graph represented using the adjacency
// matrix
void primMST(int graph[V][V])
{
// Array to store constructed MST
int parent[V];
// Array to store the Key values used to pick minimum weight edge in cut
int key[V];
// boolean array to check if vertex is included in MST set or not
bool mstSet[V];
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;
// Always include first 1st vertex in MST.
// Make key 0 so that this vertex is picked as first vertex.
key[0] = 0;
parent[0] = -1; // First node is always root of MST
// The MST will have V vertices
for (int count = 0; count < V - 1; count++)
{
// Pick the minimum key vertex from the
// set of vertices not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of
// the adjacent vertices of the picked vertex.
// Consider only those vertices which are not
// yet included in MST
for (int v = 0; v < V; v++)
// graph[u][v] is non zero only for adjacent vertices of m
// mstSet[v] is false for vertices not yet included in MST
// Update the key only if graph[u][v] is smaller than key[v]
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
// print the constructed MST
printMST(parent, graph);
}
// Driver code
int main()
{
int graph[V][V] = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
// Print the solution
primMST(graph);
return 0;
}Output of Above Program
Complexity Analysis
Kruskal’s Algorithm
- Adjacency Matrix Representation:
- Time Complexity: O(V2)
- Space Complexity: O(V2)
- Adjacency List Representation:
- Time Complexity: O(ElogE + ELogV)
- Space Complexity: O(V + E)
Prim’s Algorithm
- Adjacency Matrix Representation:
- Time Complexity: O(V2)
- Space Complexity: O(V2)
- Adjacency List Representation (Using Min Heap):
- Time Complexity: O((V + E)logV)
- Space Complexity: O(V + E)
Note: V is the number of vertices, E is the number of edges in graph G.
Conclusion
- A
spanning treein data structures is a sub-graph that includes all vertices, devoid of cycles, and always connected with a minimal set of edges. - A
Minimum Spanning Tree (MST)in a graph is the smallest tree that connects all vertices while minimizing the total edge weight. Kruskal's Algorithmis a greedy approach which includes sorting edges by weight and adding the smallest non-cycle edges to construct MST.Prim's Algorithmis a greedy approach which includes selecting minimum weight edges and expanding MST from a starting vertex, choosing nearest vertices.