Data structures are formats for organizing, processing, storing, and retrieving data. They can range from simple integer or character data types to more complex structures such as trees and maps. When we run a computer program, we might need to sort the data in a certain order. This is where sorting algorithms come into use. In this article, we shall discuss well-known sorting approaches and some commonly used sorting algorithms.
Scope
- This introductory article discusses sorting values in data structures.
- The article also introduces the idea of complexity: a way to compare the efficiencies of different sorting algorithms.
- Categories of sorting approaches, as well as examples of common sorting algorithms, are shown.
- Very short descriptions of common sorting techniques are tabulated. Implementation of algorithms using code is not shown.
Takeaways
- Time Complexity and Space complexity are standard ways to judge efficiency of a sorting algorithm.
- Appropriate sorting algorithm is choosen based on available resource constraints.
Introduction
When sorting large quantities of data, it is not enough for an algorithm to be accurate. It must minimize both the time required and the space required to perform the sorting operations.
Imagine you are the owner of a new cafe that opened a month ago. You want to figure out what’s the usual number of customers who visit your cafe on any given day. You look into your computer, and it has records of the daily customer footfall from the last 30 days. You can’t take the average, because on the opening day of the cafe, you invited a movie star to inaugurate the cafe and so, the average is distorted by the many hundreds of customers who showed up on the opening day. What do you do? You need to get your computer to calculate the median daily footfall.
How does it calculate the median? The computer algorithm needs to first sort the footfall data from the past 30 days in ascending order, temporarily store this sorted list of numbers somewhere, and then scan this sorted list for the median (middle) number.
Sounds a bit cumbersome, but okay! Shouldn’t be a problem for a computer.
Now imagine, if Facebook decided to find the median age of all of its ~3 billion users, or if the Indian Government, in its census, wanted to calculate the median income of the country’s ~300 million households. Think of the massive amounts of processing time, computer memory space, and complexity such an exercise would require! Most computers would not be able to run such an operation.
Sorting numerical data in ascending order is just one type of requirement. Other programs or other applications might need to sort large amounts of disorganized data (of different types) into chronological order, alphabetical order, or some other kind of order. The algorithms we design to do such sorting, must be efficient even as the size of the inputs scale. Just being accurate isn’t enough. When dealing with large amounts of data, it is important for algorithms to minimize both the time required and the space required to perform the sorting operations.
Or else, running any such algorithm might get very costly (in time and money terms).
The Complexity of Sorting Algorithms
- As input sizes of algorithms increase, the degree of increase in execution time and in runtime space used are mathematically called Time Complexity and Space Complexity, respectively.
- Comparing these two complexities of different algorithms can help us choose the right algorithm for our use case, based on our priorities
When we design a sorting algorithm for a particular use case, we must keep in mind the cost of running the algorithm in terms of time required, space required and other applicable factors (money, an effort to code, etc).
Depending on which algorithm you choose, the processing time or memory (space) required during execution may shoot up significantly as input sizes (number of elements to sort) get larger and larger.
For some sorting algorithms, this increase in time or space required may be linear; i.e. it proportionally increases with the number of inputs given (N). In some other algorithms, the increase in time or space required shoots up polynomially (N^2 or a higher factor).
This degree of increase in “execution time” and in “runtime space used” are mathematically called Time Complexity and Space Complexity, respectively.
You may observe mathematical notations of complexity such as O(N) or O(logN). We will not discuss the math in this article.
We may also notice that some algorithms are efficient in their space usage, while not being efficient in their time usage. Or we may observe the reverse. If we need to compare several algorithms to choose from, depending on our priorities (minimising time or minimizing space), it helps to compare the Time and Space complexities of the algorithms.
Types of Sorting Techniques
(1) In-place Sorting and Not-in-Place Sorting
In some sorting techniques, the elements to be sorted don’t require any additional space or memory to perform the sorting. Such a technique of sorting is called in-place sorting.
- For example, if you have a stack of
10answer scripts in your hands, and you want them sorted in ascending order of student roll numbers, it is possible to rearrange them in your hands, without you having to move the answer scripts to an additional workspace such as a table. - Examples: Insertion Sort, Quick Sort
In other techniques, the elements to be sorted may be stored in a temporary additional space, and then the . Since the elements are moved or copied to a different memory location during the process, the technique is called not-in-place sorting
- For example, if you have three cars parked one-behind-the-other inside a narrow, closed garage, and if you want to rearrange the cars in a different order, you’ll have to move the cars into a temporary space outside the garage, before you can re-park the cars inside the garage, in the desired order
- Example: Merge Sort
(2) Adaptive and Non-Adaptive Sorting
An adaptive sorting algorithm can take advantage of the fact that some part (subset) of the input elements are already sorted or in the desired order, and thus is able to reduce the overall effort of sorting
- For instance if you need to sort the numbers
[2,3,4,5,1]in ascending order, and you realise that part[2,3,4,5]is already sorted, then you may reduce the overall effort by shifting only the element[1]to the beginning of the list - Example: Shell Sort
A non-adaptive sorting algorithm runs the same way, irrespective of the pre-existing order of elements
- Examples: Bubble Sort, Merge Sort
(3) Stable and Unstable Sorting
Imagine you have a data table stored in Excel or Google Sheets, which contains information about all the lectures that were conducted in a college in the month of March. Two of the columns in the table are “Lecture_Date” and “Instructor_Name”. Assume that at first, all the records in the table are in random order.
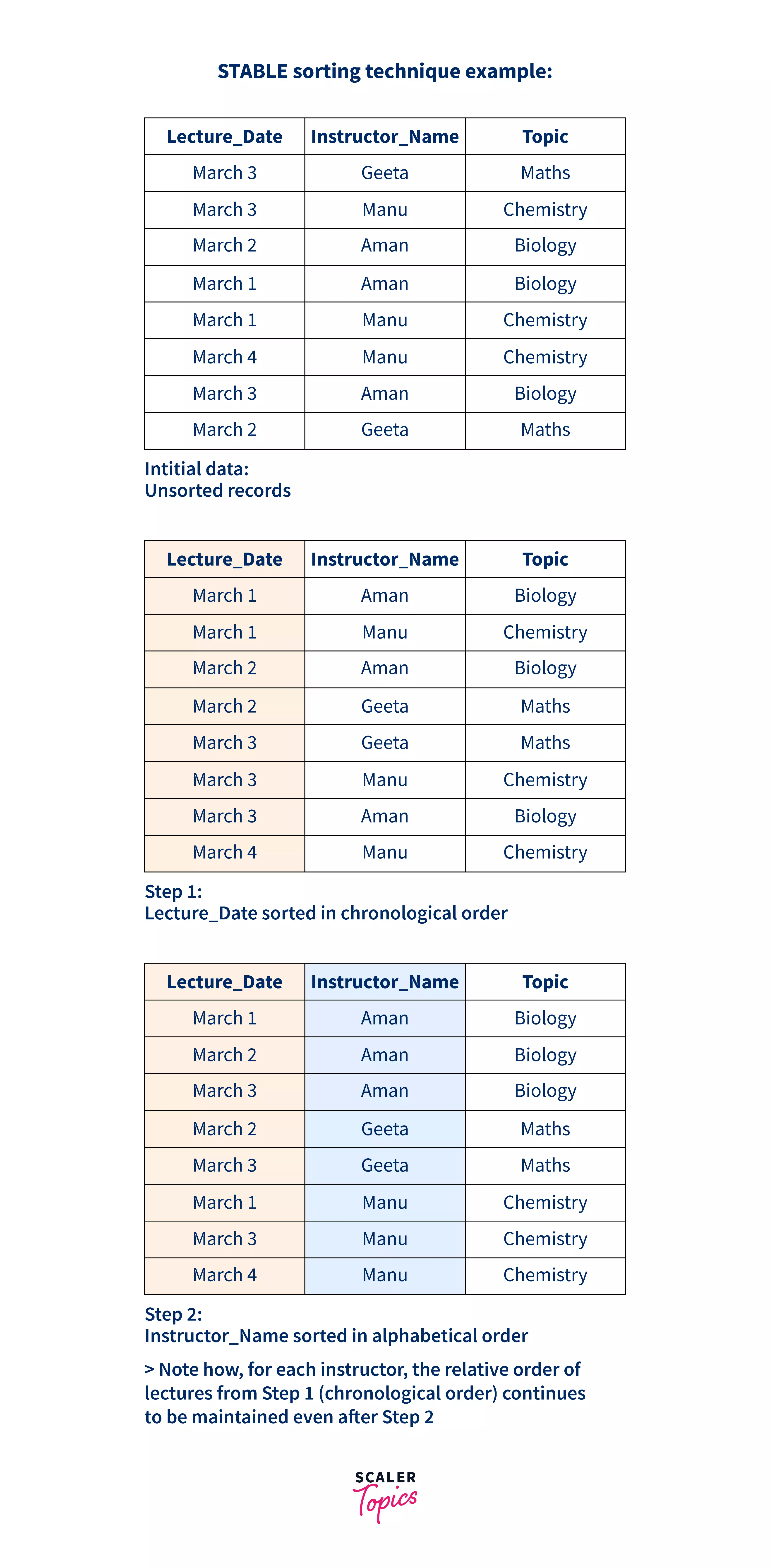
In the above image, if you sort the LectureDate column in chronological order (Step 1), and after this you sort the InstructorName column in alphabetical order (Step 2), you will see that Step 2 is accomplished, and among the rows of data for any particular Instructor, the lectures continue to be sorted in chronological order (sorting order from Step 1 is retained). Such a sorting technique is called a Stable sorting Technique, and in this, similar (or equal) elements from the sort list retain their relative order of appearance from prior to the sorting process.
- Examples: Bubble Sort, Insertion Sort, Merge Sort
(3b) Below is an example of an unstable sorting technique:
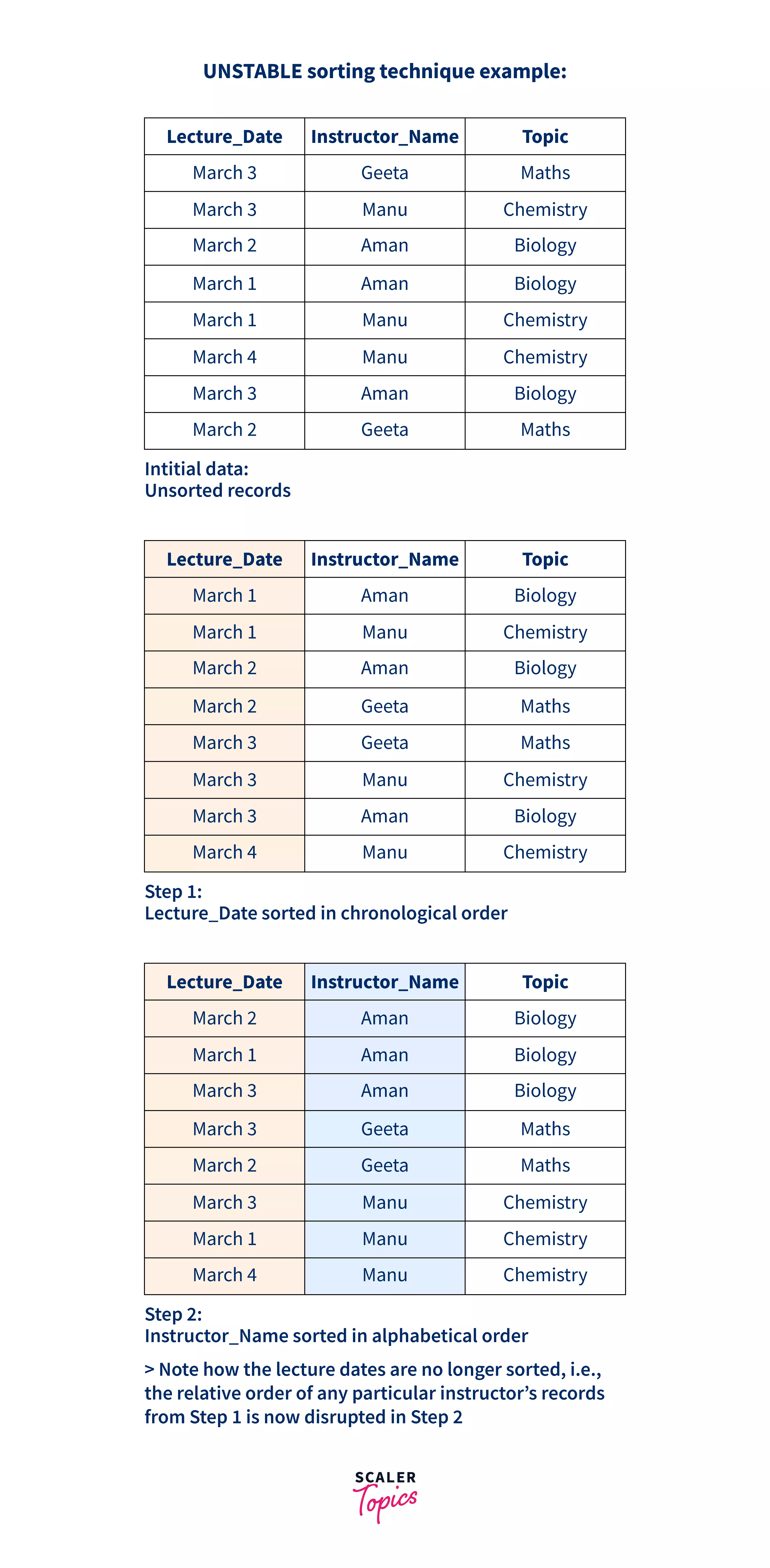
As you can observe, the similar (equal) elements in sorting step 2 did not retain their relative order from before the sort (before step 2, they were all in chronological order). Step 2 succeeded, but the relative order which existed prior to Step 2 is lost.
- Examples: Quick Sort, Heap Sort
Common Sorting Algorithms
| Algorithm | Description |
|---|---|
| Bubble Sort | Bubble sort is a comparison sort technique, where pairs of elements are compared at a time, across multiple iterations; and in the process, smaller (or larger) elements “bubble up” to the top of the list until the whole list is sorted |
| Selection Sort | Selection sort is an in-place sort technique, which divides the input into a sorted region and an unsorted region. In each iteration, the algorithm picks an appropriate element from the unsorted region and appends it to the sorted region |
| Insertion Sort | Insertion sort in another in-place technique. In each iteration, one element is chosen and inserted in its rightful place as per the desired sorted list |
| Merge Sort | Merge Sort is a recursive divide-and-conquer technique, where the original list is, in multiple iterations, broken down into smaller and smaller sub-lists until there are only single element sub-lists. Now, the algorithm reverses direction and stitches up smaller sub-lists into larger sorted lists, until we come back up to one single sorted list. |
| Quick Sort | Quick Sort is another recursive divide-and-conquer algorithm which also works like a comparison sort. In each iteration, a pivot element is chosen, and the remaining elements are partitioned into two sub-lists |
| Shell Sort | Shell sort is a comparison sort technique, which compares two elements on the outer edges of the list, swaps them based on a comparison rule, and progressively moves inwards while continuing to compare and swap pairs of elements. While Shell sort is not a stable algorithm, it is an adaptive algorithm which works better on partially sorted inputs |
Conclusion
- Sorting algorithms are used to sort data in various ways.
- Every sorting algorithm comes at a cost: it may use up lots of time or lots of extra space, or both.
- Time Complexity and Space Complexity are standard ways to compare costs.
- We should choose the most appropriate algorithm based on our resource constraints.