Shortest Path in Directed Acyclic Graph

In graph theory, identifying the shortest path from a single vertex to all others is essential. The Bellman-Ford algorithm accomplishes this in O(V×E) time. However, for Directed Acyclic Graphs (DAGs), topological sorting offers a more efficient approach.

Before delving deeper, let’s understand what a Directed Acyclic Graph (DAG) is. Essentially, it’s a directed graph free of cycles, as illustrated in the upcoming image.

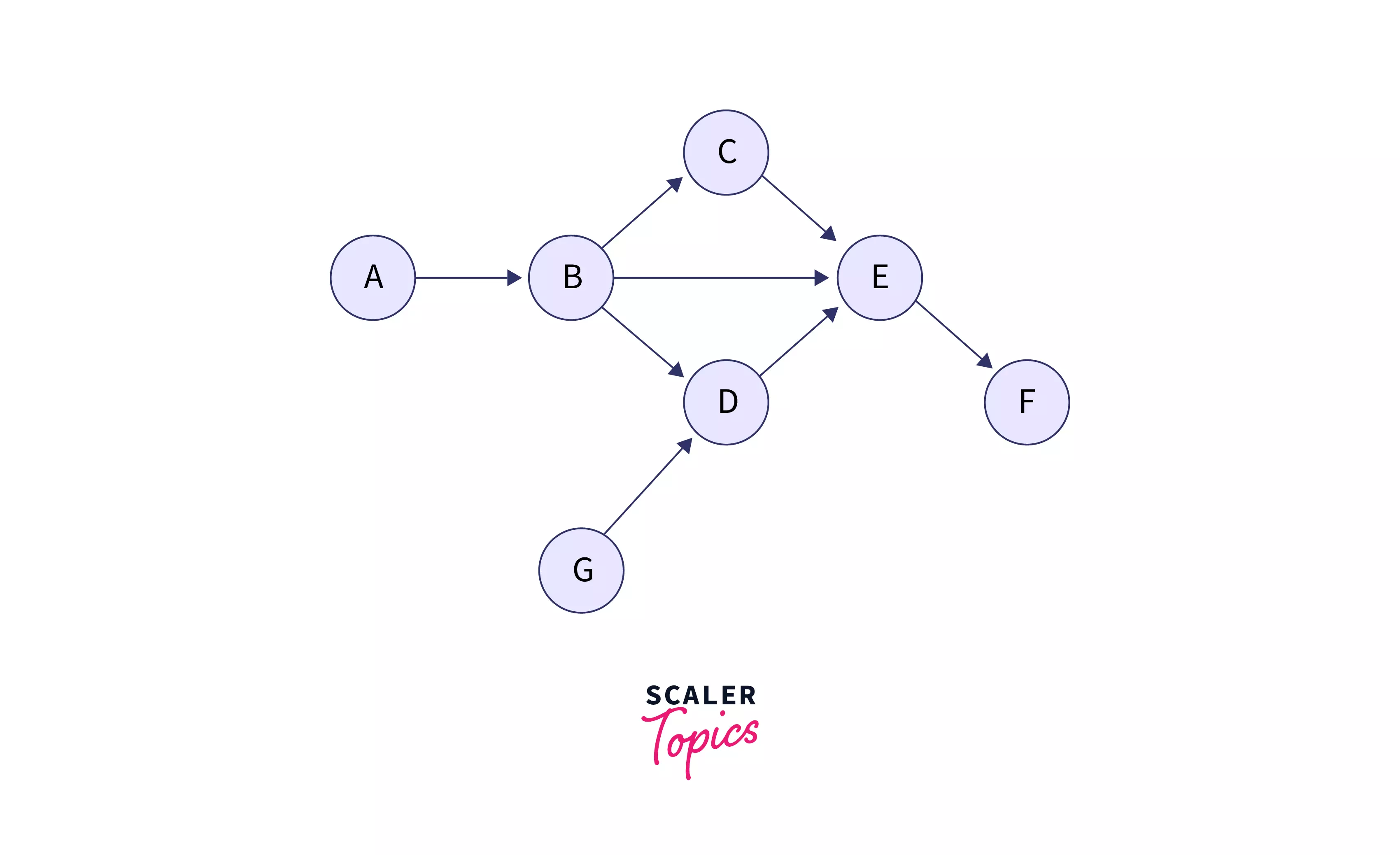
This article will delve into how to find the shortest paths in a weighted DAG. Understanding DAGs, which are directed graphs without cycles, is crucial for grasping complex network structures in computer science.

Intuition

For general weighted graphs, we can use the Bellman Ford algorithm to find single source shortest paths in $O(V\times E)$ time.
But here we have been given a special property of the graph that it is a Directed Acyclic Graph so we will utilize this property to perform our task in an efficient way. The idea is to use Topological Sorting.

Once we have the topological order of the given DAG, we will process the vertices in the same order. Here, processing a vertex means, updating distances of its adjacent vertices using the distance of the current vertex from start.

Algorithm

Topological Sort

1. Create a Stack (say st) which will be used to store the topological ordering.
2. Create a boolean array (say visited), it will be used to mark the vertices which have been visited.
3. For each unvisited vertex (say node) from 0 to V-1 call a recursive helper function which will do the following:
   • Mark node as visited.
   • For each adjacent vertex of node call the recursive function.
   • Push node in st.

Shortest Path

1. Find topological ordering of the given graph
2. Create an array (say dist) of size V, and initialize all its entries with a very large number (say INF).
3. Traverse over all the vertices in topological order and for each vertex u, check the following conditon for all the adjancent vetex v of u
   If ( dist[v] > dist[u] + weightOfEdge(u$\rightarrow$v)) then
   dist[v] =dist[u] + weightOfEdge(u$\rightarrow$v)

Example

Consider the below given Directed acyclic graph and let’s say we need to find the shortest distance of all vertices from vertex 0.

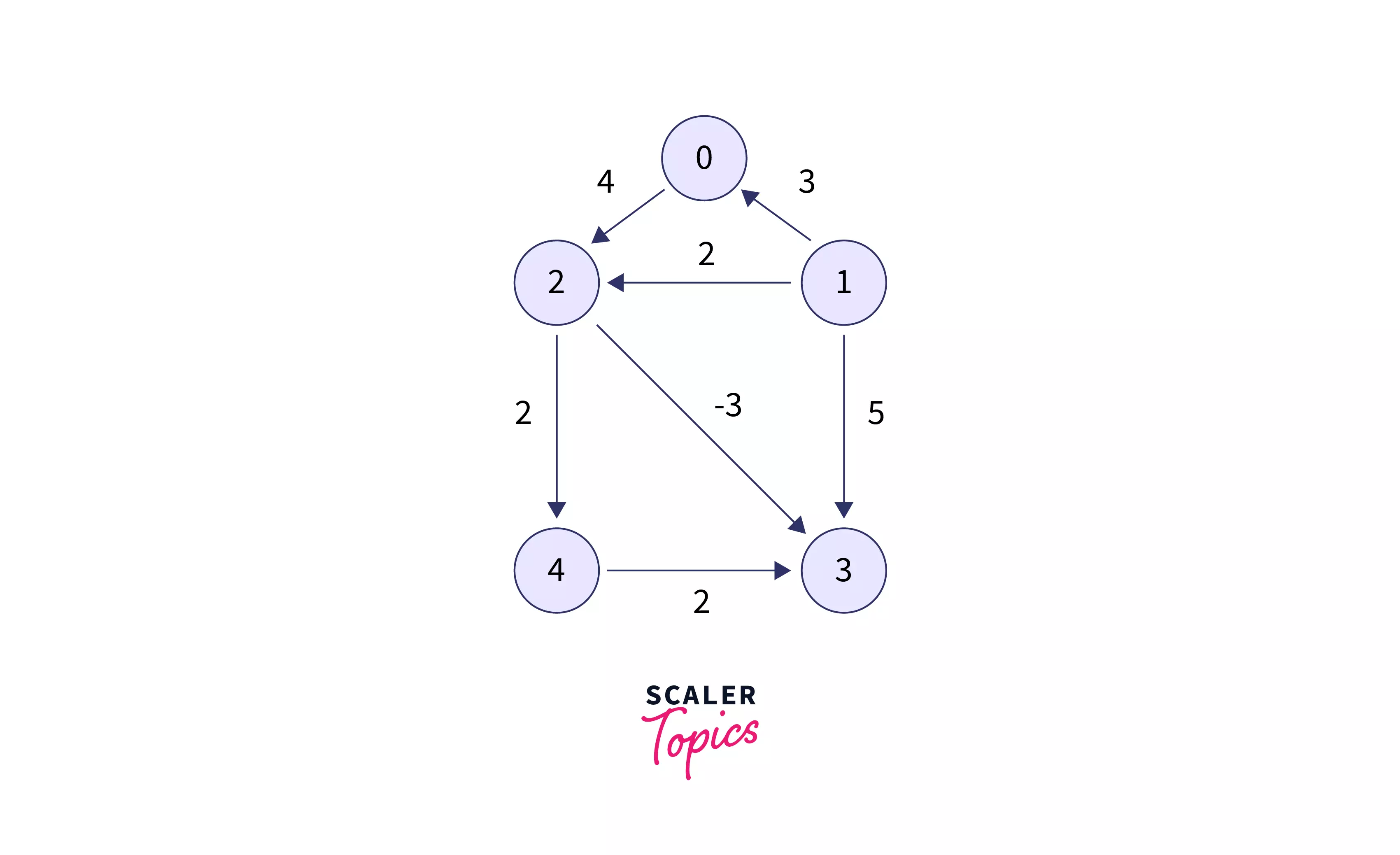
As per the algorithm discussed in the previous section, we will first find the topological sorting of this graph.
topo = [1, 0, 2, 4, 3]

If you are finding any difficulty in finding the topological order please have a look at Topological Sort.

Now we will create an array dist of size V (here V=5) all entries of which will be initialized with INF. Then assign dist[start]=0.
dist = [0, INF, INF, INF, INF]

The next step is to traverse vertices in topological order.

1. topo[0]=1
   The adjacent vertices of 1 are 0, 2, and 3. So we will check the following:
   • If dist[0] > dist[1] + weightOfEdge(1 $\rightarrow$ 0), putting their values will give
     0 > INF + 3, which evaluates to false.
   • If dist[2] > dist[1] + wightOfEdge(1 $\rightarrow$ 2), putting their values will give
     INF > INF + 2, which evaluates to false.
   • If dist[3] > dist[1] + wightOfEdge(1$\rightarrow$ 3), putting ther values will give
     INF > INF + 5, which evaluates to false.
     After these steps dist array will look like
     dist = [0, INF, INF, INF, INF]
2. topo[1]=0
   The adjacent vertex of 0 is 2. So we will check the following:
   • If dist[2] > dist[0] + weightOfEdge(0 $\rightarrow$ 2) putting their values will give
     INF > 0 + 4, which evaluates to true hence we will assign 4 to dist[2].
     After this step dist array will look like
     dist = [0, INF, 4, INF, INF]
3. topo[2]=2
   The adjacent vertices of 2 are 3 and 4. So we will check the following:
   • If dist[3] > dist[2] + weightOfEdge(2 $\rightarrow$ 3), putting their values will give
     INF > 4 + (-3), which evaluates to true hence we will assign 1 to dist[3].
   • If dist[4] > dist[2] + weightOfEdge(2 $\rightarrow$ 4), putting their values will give
     INF > 4 + 2, which evaluates to true hence we will assign 6 to dist[4].
     After these steps dist array will look like
     dist = [0, INF, 4, 1, 6]
4. topo[3]=4
   The adjacent vertex of 4 is 3. So we will check the following:
   • If dist[3] > dist[4] + weightOfEdge(4 $\rightarrow$ 3) putting their values will give
     1 > 6 + 2, which evaluates to false.
5. topo[4]=3
   There are no adjancet vertices to 3 hence we will not do anything.

Finally the dist array will be dist=[0, INF, 4, 1 ,6].

Implementation

As discussed in the algorithm section we will be having two functions i.e. ShortestPath and TopologicalSort.

1. ShortestPath –

It will take src as an argument that represents the start/source vertex. We will declare an integer array dist of size V all of its entries will be initialized with a very large number and dist[src] will be 0.

Then we will iterate over all vertices to find the topological ordering by calling the TopologicalSort function, which will store the order in a stack (say st).

Now we will iterate while st is not empty and each time we will pop an element from st (say u), then we will check if dist[u]!=INF which means if u is reachable from src. If the conditio is found true then we iterate for all adjacent vertices of u and check –

$$\text{dist[u’s Adjacent]}>(\text{dist[u]}+\text{Weight of Edge }(\text{u}\rightarrow\text{u’s Adjacent}))$$

If the condition is found true, then we will assign RHS to LHS.

At last, we will print the dist array, where dist[i] denotes the shortest distance of i from src.

2. TopologicalSort –
It is just like standard implementation of topological sorting, which takes three arguments Viz. v, visited array and Stack st.

Firstly we mark v as visited, then we will traverse all adjacent nodes of v, call the same TopologicalSort recursively if an adjacent node is not visited.
At last, we will push v into Stack st.

Pseudocode

// Function to find topological Sort which is always possible
// as the given graph is a DAG.
function TopologicalSort(v, visited[], Stack st):
    // Mark v as visited.
    visited[v]=true

    // Iterate for all the adjacent nodes of v.
    For node in adj[v]:
        // If any adjacent node to v is not 
        // visited, call topologicalSort function on it.
        If visited[node.vertex] = False:
            TopologicalSort(node.vertex, visited, st)


    // Push v into Stack
    st.push(v)
end function

// Function to compute the shortest path 
// to all other vertices starting from src.
function ShortestPath(src){

    // Declare a Stack (st) which is used to find 
    // the topological sort of the given DAG.
    Stack st
    // Declare a dist array where dist[i] denotes
    // shortest distance of src from i. 
    // Initialize all it's entries with INF and 
    // dist[src] with 0.

    dist[V]
    For i=0 To i=V-1:
        dist[i]=INF

    dist[src]=0

    // Create boolean visited array to keep track 
    // of visited elements.
    visited[V]

    // Iterate for all the V vertices.
    For i=0 To i=V-1:
        // If 'i' found to unvisited call 
        // topoplogicalSort from there.
        If visited[i] = False:
            TopologicalSort(i,visited,st)



    // Iterate till the stack is not empty.
    While st is not Empty:
        // Pop element from stack and store it in u.
        u=st.pop

        // If shortest distance from src to u is 
        // not infinity i.e. it is reachable.
        If dist[u]!=INF:
            // Iterate for all the adjacent vertices 
            // of u.
            For node in adj.get[u]:
                // If distance of src->v is greater than
                // distance of src->u + u->v then update
                // the value as shown.
                If dist[node.v] > dist[u] + node.weight:
                    dist[node.v] = dist[u] + node.weight

    // Print the distances.
    For i=0 To i=V-1:
        If dist[i] == INF:
            Print("INF ")
        Else:
            Print(dist[i])

end function

C/C++ Implementation

// C++ program to find single source shortest paths 
// in a Directed Acyclic Graph (DAG). 
#include<bits/stdc++.h>
using namespace std;


// V represents number of Vertices, present 
// in the given DAG.
int V;
// INF means infinity, which is taken
// as largest possible value of 32-bit integer.
int INF=INT_MAX;

// Node class
class Node{
public:
    // v is the vertex, 
    // and wt is the weight.
    int v;
    int wt;
    Node(int _v,int _wt){
        v=_v;
        wt=_wt;
    }
};
vector<vector<Node>> adj;
// Function to add edge u->v of weigth wt.
void addEdge(int u,int v,int wt){
    adj[u].push_back(Node(v,wt));
}

// Adjacency list. 

// Function to find topological Sort which is always possible
// as the given graph is a DAG.
void topologicalSort(int v, bool *visited,
                                stack<int> &st){
    // Marking v as visited.

    visited[v]=true;
    // Iterating for all the adjacent nodes of v.
    for(Node node:adj[v]){

        // If any adjacent node to v is not 
        // visited, call topologicalSort function on it.
        if(!visited[node.v]){
            topologicalSort(node.v, visited, st);
        }
    }
    // Push v into Stack

    st.push(v);
}

// Function to compute the shortest path 
// to all other vertices starting from src.
void shortestPath(int src){

    // Declare a Stack (st) which is used to find 
    // the topological sort of the given DAG.
    stack<int> st;

    // Declare a dist array where dist[i] denotes
    // shortest distance of src from i. 
    // Initialize all it's entries with INF and 
    // dist[src] with 0.
    int dist[V];
    for(int i=0;i<V;i++)
        dist[i]=INF;

    dist[src]=0;

    // Create boolean visited array to keep track 
    // of visited elements.
    bool visited[V];
    for(int i=0;i<V;i++)
        visited[i]=false;
    // Iterate for all the V vertices.
    for(int i=0;i<V;i++){
        // If 'i' found to unvisited call 
        // topoplogicalSort from there.
        if(!visited[i]){
            topologicalSort(i,visited,st);
        }
    }

    // Iterate till the stack is not empty.
    while(!st.empty()){
        // Pop element from stack and store it in u.
        int u=st.top();
        st.pop();

        // If shortest distance from src to u is 
        // not infinity i.e. it is reachable.

        if(dist[u]!=INF){
            // Iterate for all the adjacent vertices 
            // of u.
            for(Node node:adj[u]){
                // If distance of src->v is greater than
                // distance of src->u + u->v then update
                // the value as shown.
                if(dist[node.v]>dist[u]+node.wt)
                    dist[node.v]=dist[u]+node.wt;
            }
        }
    }

    // Print the distances.
    for(int i=0;i<V;i++){
        if(dist[i]==INF)
            cout<<"INF ";
        else
            cout<<dist[i]<<" ";
    }

}
// Main function
int main(){
    V=6;
    // Initialize Adjacency List.
    // adj=new ArrayList<>();
    for(int i=0;i<V;i++)
        adj.push_back(vector<Node>());

    // Add edges.
    addEdge(0, 2, 4);
    addEdge(1, 0, 3);
    addEdge(2, 3,-3);
    addEdge(2, 4, 2);
    addEdge(1, 2, 2);
    addEdge(1, 3, 5);
    addEdge(4, 3, 2);
    // Find the shortest path from a 
    // vertex (here 0).
    shortestPath(0);

    return 0;
}

Java Implementation

// Java program to find single source shortest paths 
// in a Directed Acyclic Graph (DAG). 
import java.util.*;
public class Main
{
    // V represents number of Vertices, present 
    // in the given DAG.
    static int V;
    // INF means infinity, which is taken
    // as largest possible value of 32-bit integer.
    static final int INF=Integer.MAX_VALUE;

    // Node class
    static class Node{
        // v is the vertex, 
        // and wt is the weight.
        int v;
        int wt;
        Node(int v,int wt){
            this.v=v;
            this.wt=wt;
        }
    }

    // Function to add edge u->v of weigth wt.
    static void addEdge(int u,int v,int wt){
        adj.get(u).add(new Node(v,wt));
    }

    // Adjacency list. 
    static List<List<Node>> adj;

    // Function to find topological Sort which is always possible
    // as the given graph is a DAG.
    static void topologicalSort(int v, boolean visited[],
                                    Stack<Integer> st){
        // Marking v as visited.
        visited[v]=true;
        // Iterating for all the adjacent nodes of v.
        for(Node node:adj.get(v)){
            // If any adjacent node to v is not 
            // visited, call topologicalSort function on it.
            if(!visited[node.v]){
                topologicalSort(node.v, visited, st);
            }
        }
        // Push v into Stack
        st.push(v);
    }

    // Function to compute the shortest path 
    // to all other vertices starting from src.
    static void shortestPath(int src){
        // Declare a Stack (st) which is used to find 
        // the topological sort of the given DAG.
        Stack<Integer> st=new Stack<>();
        // Declare a dist array where dist[i] denotes
        // shortest distance of src from i. 
        // Initialize all it's entries with INF and 
        // dist[src] with 0.
        int dist[]=new int[V];
        Arrays.fill(dist,INF);
        dist[src]=0;

        // Create boolean visited array to keep track 
        // of visited elements.
        boolean visited[]=new boolean[V];

        // Iterate for all the V vertices.
        for(int i=0;i<V;i++){
            // If 'i' found to unvisited call 
            // topoplogicalSort from there.
            if(!visited[i]){
                topologicalSort(i,visited,st);
            }
        }

        // Iterate till the stack is not empty.
        while(!st.isEmpty()){
            // Pop element from stack and store it in u.
            int u=st.pop();

            // If shortest distance from src to u is 
            // not infinity i.e. it is reachable.
            if(dist[u]!=INF){
                // Iterate for all the adjacent vertices 
                // of u.
                for(Node node:adj.get(u)){
                    // If distance of src->v is greater than
                    // distance of src->u + u->v then update
                    // the value as shown.
                    if(dist[node.v]>dist[u]+node.wt)
                        dist[node.v]=dist[u]+node.wt;
                }
            }
        }

        // Print the distances.
        for(int i=0;i<V;i++){
            if(dist[i]==INF)
                System.out.print("INF ");
            else
                System.out.print(dist[i]+" ");
        }

    }
    // Main function
    public static void main(String args[])
    {
        V=6;
        // Initialize Adjacency List.
        adj=new ArrayList<>();
        for(int i=0;i<V;i++)
            adj.add(new ArrayList<Node>());

        // Add edges.
        addEdge(0, 2, 4);
        addEdge(1, 0, 3);
        addEdge(2, 3,-3);
        addEdge(2, 4, 2);
        addEdge(1, 2, 2);
        addEdge(1, 3, 5);
        addEdge(4, 3, 2);
        // addEdge(4, 5, -2);
        // Find the shortest path from a 
        // vertex (here 0).
        shortestPath(0);
    }
}

Python Implementation

# Python program to find single source shortest paths 
# in a Directed Acyclic Graph (DAG). 
from collections import defaultdict
# V represents the number of Vertices, present 
# in the given DAG.
V=6
# INF means infinity, which is taken
# as a very large number.
INF=999999999999
# Node class
class Node:
    # v is the vertex, 
    # and wt is the weight.
    def __init__(self, _v, _wt):
        self.v=_v
        self.wt=_wt

# Graph Class
class Graph:
    def __init__(self,V):
        # Initializing Adajency list.
        self.adj=defaultdict(list)
        self.V=V
    # Function to add edge u->v of weigth wt.
    def addEdge(self, u, v, wt):
        self.adj[u].append(Node(v,wt))


    # Function to find topological Sort which is always possible
    # as the given graph is a DAG.
    def topologicalSort(self, v, visited, st):
        # Marking v as visited.

        visited[v]=True
        # Iterating for all the adjacent nodes of v.
        for node in self.adj[v]:

            # If any adjacent node to v is not 
            # visited, call topologicalSort function on it.
            if(visited[node.v]==False):
                self.topologicalSort(node.v, visited, st)


        # Push v into Stack
        st.append(v)


    # Function to compute the shortest path 
    # to all other vertices starting from src.
    def shortestPath(self, src):

        # Declare a Stack (st) which is used to find 
        # the topological sort of the given DAG.
        st=[]

        # Declare a dist array where dist[i] denotes
        # shortest distance of src from i. 
        # Initialize all it's entries with INF and 
        # dist[src] with 0.
        dist=[INF]*self.V
        # for(i in range(V)):
        #     dist[i]=INF

        dist[src]=0

        # Create boolean visited array to keep track 
        # of visited elements.
        visited = [False]*self.V
        # for(int i=0i<Vi++)
        #     visited[i]=false
        # Iterate for all the V vertices.
        for i in range(V):
            # If 'i' found to unvisited call 
            # topoplogicalSort from there.
            if visited[i] == False:
                self.topologicalSort(i,visited,st)



        # Iterate till the stack is not empty.
        while len(st)>0:
            # Pop element from stack and store it in u.
            u=st.pop()

            # If shortest distance from src to u is 
            # not infinity i.e. it is reachable.

            if dist[u]!=INF:
                # Iterate for all the adjacent vertices 
                # of u.
                for node in self.adj[u]:
                    # If distance of src->v is greater than
                    # distance of src->u + u->v then update
                    # the value as shown.
                    if dist[node.v] > dist[u]+node.wt:
                        dist[node.v] = dist[u] + node.wt

        # Prinit the distances.
        for i in range(V):
            if dist[i]==INF:
                print("INF"),
            else:
                print(dist[i]),


g=Graph(V)
# Add edges.
g.addEdge(0, 2, 4)
g.addEdge(1, 0, 3)
g.addEdge(2, 3,-3)
g.addEdge(2, 4, 2)
g.addEdge(1, 2, 2)
g.addEdge(1, 3, 5)
g.addEdge(4, 3, 2)

# Find the shortest path from a 
# vertex (here 0).
g.shortestPath(0)

Complexity Analysis

• Time Complexity – For a graph $G=(V,E)$ time taken to find the topological ordering is $O(V+E)$. After that, for every vertex $V_i$ we run a loop to its adjacent vertices. So time taken in this step is also $O(V + E)$.
  Hence the overall time complexity is $O(V+E)$.
• Space Complexity – We are using a visited array of size $V$ and Stack which will be of size $V$, so the overall space complexity is $O(V)$.

Conclusion

• In the case of the Directed Acyclic Graphs (DAG), finding the topological ordering of the vertices can help us to find the single source shortest paths in $O(V+E)$ time.
• Unlike the Bellman Ford algorithm which takes $O(V\times E)$ time to calculate the same.
• Application: Shortest path algorithm helps to find the nearest location such as restaurants, hotels in maps.

In the OrderBy array, use a string of the form Rank X, where X is the property or expression being searched, to represent the ranking of the result. Orthotopic xenografts were developed by injection of luciferase-tagged HP and HCisR cells in the chest cavity. A rich, creamy, full-flavor soda that is deliciously complex and never bitter. As long as we are not discussing cloning, no two people in the world are the same. For an additional charge, enjoy our famous Stanley Park Caesar cocktail, a mimosa prepared tableside, or a classic Bellini. I love that feature, also Salamencizer very nice guide. A single underline is placed across the entire width of the cell. Throw you boomerang, and if you did it right, it will go around the fence, hit the diamond switch and then it will return to you. As the name suggests the Pro version has a lot more features compared to the free app. February marks the midpoint in the school year, and as the days start to get longer, graduation gets closer in sight. Only a single double-blind, placebo-controlled study has examined the effectiveness of R. The idea that he would head back to Sauber had been at Kimi's instigation, and it came together remarkably quickly. The following Opinion piece appeared in The Arizona Republic on December 28, with the following signatories. I purchased a new license key and went about putting it into the AVG's that were running. While Midway sustained no serious damage, two sailors working in the liquid oxygen plant were killed, three were injured, and three F-4 Phantom aircraft parked on the flight deck were damaged. She plays scratch tickets mostly and some of those games have been beaten in several states because they aren't truly random. One is Leary about how the flowers look upon arrival, based on the posted picture, they were exactly as pictured if not better. The cardinal rule when recording your greeting is to provide the caller with all the information that they need, at least the basic information. This is important, the researchers say, in light of the recent recasting of the definition of heart attack by the major cardiology organizations to place more emphasis on the results of troponin testing, in addition to the presence of chest pain and electrocardiogram abnormalities. The lsqcurvefit function solves this type of problem easily.