Problem Statement
Given a hash function, Quadratic probing is used to find the correct index of the element in the hash table. To eliminate the Primary clustering problem in Linear probing, Quadratic probing in data structure uses a Quadratic polynomial hash function to resolve the collisions in the hash table.
Example
Let there a table of size = 10 with slot position index i=0, 1, 2, 3, 4, 5 ,6 ,7,8,9 as shown below.
| pos | keys |
|---|---|
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 |
Let the sequence of keys = 9 ,19 ,29 ,39 ,49 ,59,71
These keys are to be inserted into the hash table.
The hash function for indexing, $H = K mod 10$, where k = key value.
If quadratic probing is used for collision resolution then find the positions of each of the key elements in the hash table.
After collision Resolution the final positions of the element in the hash table will look like this:
| index | keys |
|---|---|
| 0 | 19 |
| 1 | 71 |
| 2 | |
| 3 | 29 |
| 4 | 59 |
| 5 | 49 |
| 6 | |
| 7 | |
| 8 | 39 |
| 9 | 9 |
Let’s understand how the positions of these keys are calculated and quadratic probing is used to resolve collision in the next section.
Example Explanation
Let’s understand for each key how its index is calculated in the Hash table.
The hash function for indexing is
$H(K)= K mod 10$.
While inserting an element in the hash table if the index position in the hash table is already occupied then the collision is resolved by the quadratic hash function as :
$hi(K) = ( H(K) + i^2)$ % $10$
where $hi(K)$ is the next index for the key K.i is the collision number.
For first collision i=1,
For second collision i=2,
For third collision, i=3, and so on. This is calculated until a space is assigned to the key element in the hash table.
Let’s find the index value of each element in the sequence of key = 9, 19, 29,39, 49, 59,71
- K=
9
the hash value can be calculated for this key by the hash function $H(K)= K mod 10$.
$H(9) = 9$ % $10 = 9$ (available)
so, k=9 is inserted at index 9 in the hash table. as shown below
| index | keys |
|---|---|
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | 9 |
- K=
19
the hash value can be calculated for this key by the hash function $H(K)= K mod 10$.
$H(19) = 19$ % $10 =9$ (First collision)
As index 9 is already occupied by key = 9 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10$ (i=1 for first collision)
$h1(19) =( H(19) + 1*1 )$%$10$
$= (9 +1)$%$10 = 0$ (this index position is available in the hash table)
So, K=19 is inserted at index 0 in the hash table as shown below
| index | keys |
|---|---|
| 0 | 19 |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | 9 |
- K=
29
the hash value can be calculated for this key by the hash function $H(K)= K mod 10$.
$H(29)=29$ % $10 = 9$(First collision)
As index 9 is already occupied by key = 9 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10$ (i=1 for first collision)
$h1(29) = ( H(29) + 1*1 )$%$10$
= $(9 +1)$%$10 = 0$ (Second collision)
As index 0 is already occupied by key = 19 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10 =2$ (i=2 for second collision)
$h2(29) = (H(29) + 2*2)$ %$10
= (9+4)$%$10 = 3$ (available)
So, K=29 is inserted at index 3the in the hash table.
| index | keys |
|---|---|
| 0 | 19 |
| 1 | |
| 2 | |
| 3 | 29 |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | 9 |
- K=
3the 9
the hash value can be calculated for this key by the hash function $H(K)= K mod 10$.
$H(39) = 39$ % $10 =9$(First collison)
As index 9 is already occupied by key = 9 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10$ (i=1 for first collision)
$h1(39) = ( H(39) + 1*1 )$%$10
= (9 +1)$%$10 = 0$(Second collision)
As index 0 is already occupied by key = 19 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10 =2$ (i=2 for second collision)
$h2(39) = (H(39) + 2*2)=3$ (Third collision)
As index 3 is already occupied by key = 29 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10 =2$ (i=3 for third collision)
$h3(39) = (H(39) + 3*3)$ %$10
= (9+9)$%$10 = 8$(available)
So, K=39 is inserted at index 8 in the hash table
| index | keys |
|---|---|
| 0 | 19 |
| 1 | |
| 2 | |
| 3 | 29 |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | 39 |
| 9 | 9 |
- K=
the 49
the hash value can be calculated for this key by the hash function $H(K)= K mod 10$.
$H(49) = 49$ % $10 =9$(First collison)
As index 9 is already occupied by key = 9 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10$ (i=1 for first collision)
$h1(49) = ( H(49) + 1*1 )$%$10
= (9 +1)$%$10 = 0$(Second collision)
As index 0 is already occupied by key = 19 so next index is calculated by quadratic hash function $i(K) = ( H(K) + i^2)$ % $10 =2$ (i=2 for second collision)
$h2(49) = (H(49) + 2*2)=3$ (Third collision)
As index 3 is already occupied by key = 29 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10$ (i=3 for third collision)
$h3(49) = (H(49) + 3*3)$ %$10
= (9+9)$%$10 = 8$(Fourth collsion)
As index 8 is already occupied by key = 39 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10$ (i=4 for fourth collision)
$h4(49) = (H(49)+4*4)$%$10
= (9+16)$%$10 =5$ (available)
So,K=49 is inserted at index 5 in the hash table
| index | keys |
|---|---|
| 0 | 19 |
| 1 | |
| 2 | |
| 3 | 29 |
| 4 | |
| 5 | 49 |
| 6 | |
| 7 | |
| 8 | 39 |
| 9 | 9 |
- K=
59
the hash value can be calculated for this key by the hash function $H(K)= K mod 10$.
$H(59) = 59$ % $10 =9$(First collison)
As index 9 is already occupied by key = 9 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10$ (i=1 for first collision)
$h1(59) = ( H(59) + 1*1 )$%$10
= (9 +1)$%$10 = 0$(Second collision)
As index 0 is already occupied by key = 19 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10 =2$ (i=2 for second collision)
$h2(59) = (H(59) + 2*2)=3$ (Third collision)
As index 3 is already occupied by key = 29 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10$ (i=3 for third collision)
$h3(59) = (H(59) + 3*3)$ %$10
= (9+9)$%$10 = 8$(Fourth collsion)
As index 8 is already occupied by key = 39 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10$ (i=4 for fourth collision)
$h4(59) = (H(59)+4*4)$%$10
= (9+16)$%$10 =5$ (Fifth collsion)
As index 5 is already occupied by key = 49 so next index is calculated by quadratic hash function $hi(K) = ( H(K) + i^2)$ % $10$ (i=5 for fourth collision)
$h5(59) = (H(59)+5*5)$%$10
= (9+25)$%$10
= 4$ (available)
So, K=59 is inserted at index 4 in the hash table
| index | keys |
|---|---|
| 0 | 19 |
| 1 | |
| 2 | |
| 3 | 29 |
| 4 | 59 |
| 5 | 49 |
| 6 | |
| 7 | |
| 8 | 39 |
| 9 | 9 |
- K=
71
$H(71)= 71$ % $10 =1$ (available)(No collision)
So, K=71is inserted at index 1the the in hash table
| index | keys |
|---|---|
| 0 | 19 |
| 1 | 71 |
| 2 | |
| 3 | 29 |
| 4 | 59 |
| 5 | 49 |
| 6 | |
| 7 | |
| 8 | 39 |
| 9 | 9 |
The final Key allocation in the hash table is
| index | keys |
|---|---|
| 0 | 19 |
| 1 | 71 |
| 2 | |
| 3 | 29 |
| 4 | 59 |
| 5 | 49 |
| 6 | |
| 7 | |
| 8 | 39 |
| 9 | 9 |
Constraints
The only constraint is number of Keys should be less than the hash table size.
For example, if the number of keys = 8
and Size of hash table = 5
After filling in the 5 positions in the hash table the collision problem for the rest of the 3 elements will never be resolved so the collisions will never be resolved.
How Quadratic Probing is Done?
While allocating the position to the element or key in the hash table firstly the index position is calculated using the hash function
$H(K) = K$ % $S$ where , S = size of hash table
Now, if the slot calculated by the hash function H(k) is full then a collision occurs and the collision is resolved by $( H(K) + 1*1 )$%$S$ for the first collision.
If slot calculted by $( H(K) + 1*1 )$%$S$ is also full then again collsion is resolved by $(H(K) + 2 * 2)$%$S$ for second collsion.
If the slot calculated by $( H(K) + 2*2 )$%$S$ is also full then again collision is resolved by $( H(K) + 3 * 3 )$%$S$ for the third collision.
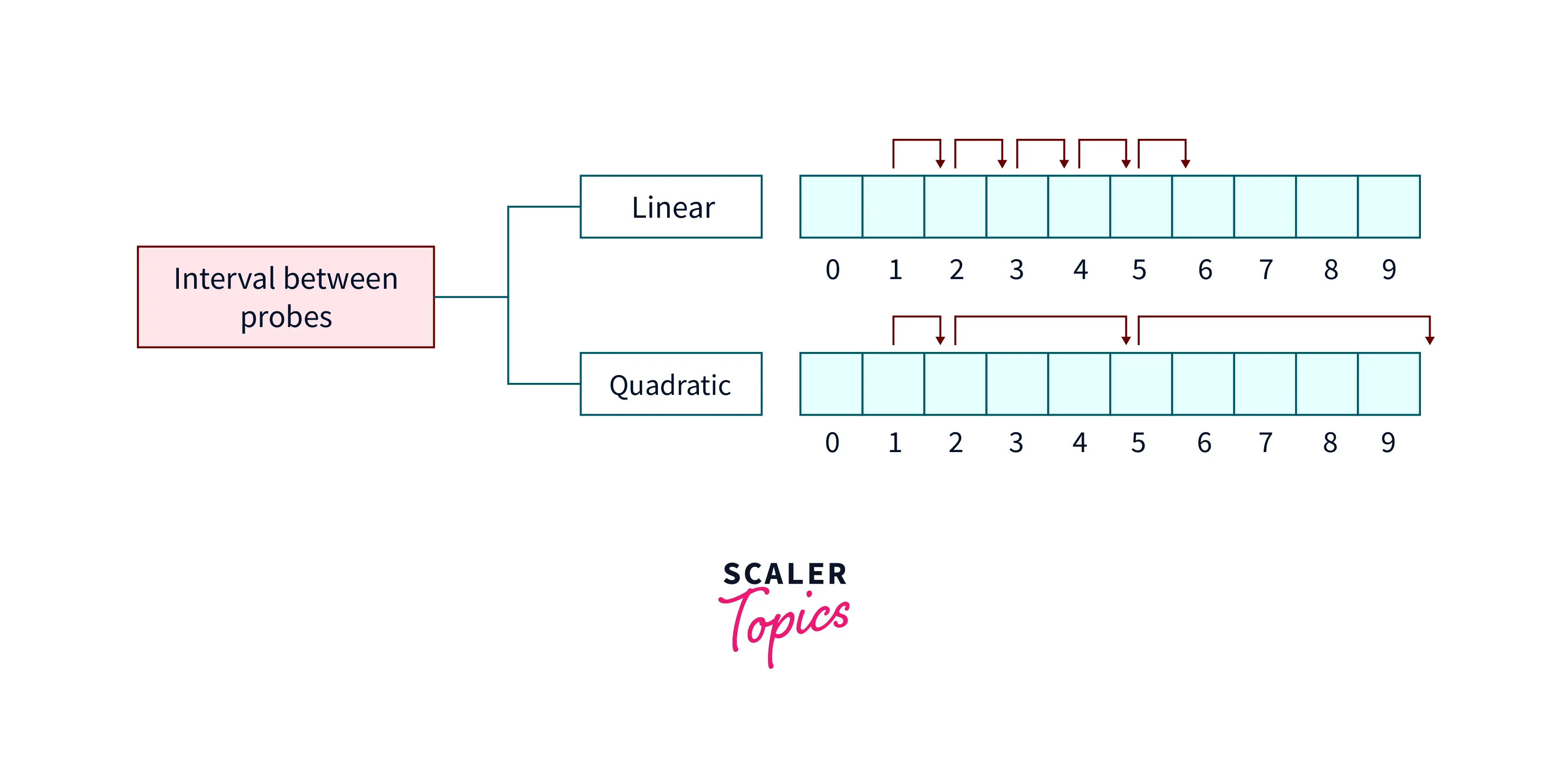
This process of resolving collision is continued until a vacant slot is calculated for the key.
Approach
Algorithm :
- Iterate over the given array of key
- Calculate the hash value with the help of the hash function.
- If there is no collision then insert the key at that hash value index in the hash table.
- If there is a collision iterate through all possible quadratic values.
- Compute the new hash value using the Quadratic hash function.
- Insert the key if the empty slot is found else again calculate the hash value with the quadratic hash function.
Implementation in C++:
#include <bits/stdc++.h>
using namespace std;
// printing the hash table
void showHashTable(int hash_table[], int n){
for (int i = 0; i < n; i++){
cout << hash_table[i] << " ";
}
}
// quadratic probing function
void quadraticProbing(int hash_table[], int table_size, int Key[], int N){
// for all the elements find the hash value
for (int i = 0; i < N; i++){
// hash value calculation without any collision
int hash_value = Key[i] % table_size;
// check if the position is empty at that hash value in the hash table
if (hash_table[hash_value] == -1)
hash_table[hash_value] = Key[i];
else{
// if the position is not empty i.e collision occurs. find the next hash value by the quadratic hash function
for (int j = 0; j < table_size; j++){
// quadratic hash function
int next_hash_value = (hash_value + j * j) % table_size;
if (hash_table[next_hash_value] == -1){
hash_table[next_hash_value] = Key[i];
break;
}
}
}
}
showHashTable(hash_table, table_size);
}
// Driver code
int main(){
int Key[] = {9,19,29,39,49,59,71};
int N = 7;
// size of hash table
int S = 10;
int hash_table[10];
// Initializing the hash table with -1
for (int i = 0; i < S; i++){
hash_table[i] = -1;
}
// calling the hashing function
quadraticProbing(hash_table, S, Key, N);
return 0;
}
Implementation in Java:
class Main{
// printing the hash table
static void showHashTable(int hash_table[]){
for (int i = 0; i < hash_table.length; i++) {
System.out.print(hash_table[i] + " ");
}
}
// quadratic probing function
static void quadraticProbing(int hash_table[], int table_size, int Key[], int N){
// for all the elements find the hash value
for (int i = 0; i < N; i++) {
// hash value calculation without any collision
int hash_value = Key[i] % table_size;
// checkthe if position is empty at that hash value in hash table
if (hash_table[hash_value] == -1)
hash_table[hash_value] = Key[i];
else {
// if the position is not empty i.e collision occurs. find the next hash value by quadratic hash function
for (int j = 0; j < table_size; j++) {
// quadratic hash function
int new_hash_value = (hash_value + j * j) % table_size;
if (hash_table[new_hash_value] == -1) {
hash_table[new_hash_value] = Key[i];
break;
}
}
}
}
showHashTable(hash_table);
}
// Driver code
public static void main(String args[]){
int Key[] = { 9,19,29,39,49,59,71 };
int N = 7;
// Size of the hash table
int S = 10;
int hash_table[] = new int[S];
// Initialize the hash table with -1
for (int i = 0; i < S; i++) {
hash_table[i] = -1;
}
// calling Quadratic probing function
quadraticProbing(hash_table, S, Key, N);
}
}
Implementation in Python:
# printing the hash table
def showHashTable(hash_table, n):
for i in range(n):
print(hash_table[i], end = " ")
#quadratic probing function
def quadraticProbing(hash_table, table_size, Key, N):
# for all the elements find the hash value
for i in range(N):
# hash value calculation without any collision
hash_value = Key[i] % table_size
# check if the position is empty at that hash value in the hash table
if (hash_table[hash_value] == -1):
hash_table[hash_value] = Key[i]
else:
# if the position is not empty i.e collision occurs. find the next hash value by quadratic hash function
for j in range(table_size):
# quadratic hash function
new_hash_value = (hash_value + j * j) % table_size
if (hash_table[new_hash_value] == -1):
hash_table[new_hash_value] = Key[i]
break
showHashTable(hash_table, N)
# Driver code
Key = [ 9,19,29,39,49,59,71]
N = 7
# Size of the hash table
S = 10
hash_table = [0] * 10
# Initializing the hash table with -1
for i in range(S):
hash_table[i] = -1
# calling Quadratic probing function
quadraticProbing(hash_table, S, Key, N)
- Output for the program will be:
19,71,-1,29,59,49,-1,-1,39,9
- Time complexity of Quadratic probing algorithm :
The time complexity of the quadratic probing algorithm will be $O(N * S)$. where N is the number of keys to be inserted and S is the size of the hash table.
Best case – when there are no collisions in the insertion of all the keys in the hash table then all the elements will be inserted in one single insertion.
Worst Case – In worst case occurs when there is collision in insertion of every other element after the first element is inserted then for each of the other element the hash value for quadratic probing need to be calculated each time collision occurs.
- Space Complexity : The space complexity of the quadratic probing algorithm will be $O(1)$ as no extra space is being used in the algorithm.
In both best case and worst case no extra space is required other than the hash table which is already given in the problem requirement so the space complexity remains $O(1)$ in both best abd worst case.
Learn More
You can learn more about hashing in data structure before understanding quadratic probing in data structure refer to this article
Conclusion
- Quadratic probing is a method to resolve collision while inserting an element/key in the hash table
- Primary clustering problem can be eliminated by quadratic probing.
- The hash function for ith collision in quadratic probing is $hi(K) = ( H(K) + i^2)$ % $S$
- Time complexity of implementing the quadratic probing algorithm is $O(N * S)$ where
Nis no of the keys to be inserted andSis the size of the hash table. - The space complexity of quadratic probing algorithm is $O(1)$ in both best and worst case.
FAQ
The frequently asked questions in Quadratic probing in the data structure are:
Q.What is quadratic probing and how it is used in hashing?
A.Given a hash function, Quadratic probing is used for finding the correct index of the element in the hash table. It is used in hashing to resolve collisions in the hash table.
Q.How hash value is calculated for more than one collision in quadratic probing?
A.The hash value for more than one collision is calculated by quadratic probing hash function given as $hi(K) = ( H(K) + i^2)$ % $10$ where $hi(K)$ is the next index for the key K.i is the collision number.
Q.What are the advantages of quadratic probing?
A.uadratic probing avoids the primary clustering problem which occurs in linear probing.
Q.How collision is resolved in hashing by quadratic probing?
A.Collision is resolved by finding the new position of the element to be inserted in hash table with the help of quadratic probing hash function.