The left view of a binary tree corresponds to the nodes of the tree, which would be visible to someone seeing the tree from its left side, as shown in the image below –
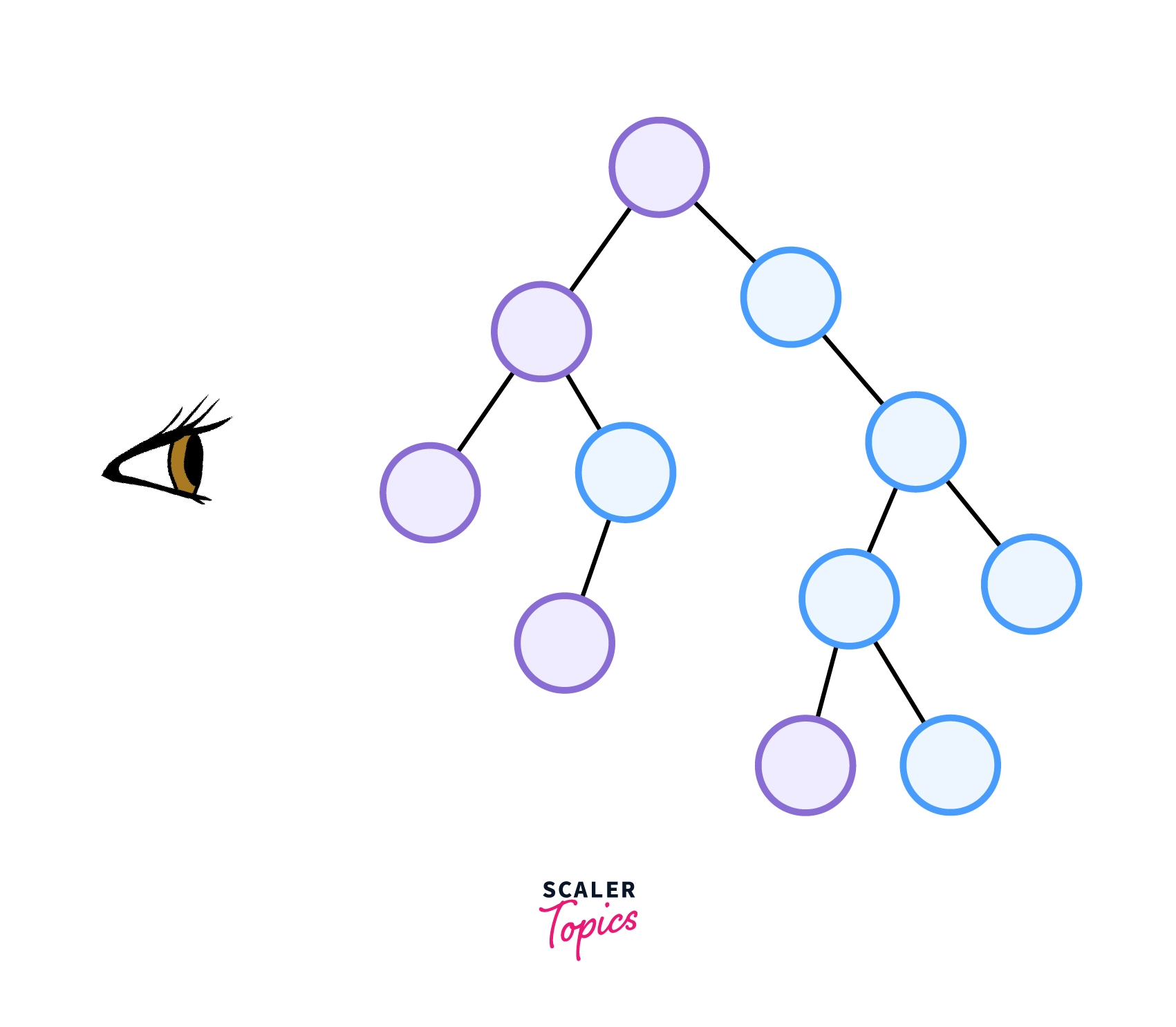
To print the left view of a binary tree, it’s essential to recognize that the leftmost node at each level is visible from the left side.
Approach-1: Using Recursion
We can print a binary tree’s left view using recursion.
Below is the implementation of the above approach –
The blueprint of code will be –
Variables –
- maxLevel – Global variable, which denotes the maxLevel traversed till now.
- level – Local variable, denoting the current level.
Methods –
- leftView – This wrapper function will call the leftView_Helper function passing root with the current level as 0.
- leftView_Helper – It will check whether the current level is greater than maxLevel. If yes, we will include the node in the answer and update the maxLevel. At last, we will recurse for the left subtree and then for the right subtree.
C/C++
#include<bits/stdc++.h>
using namespace std;
// TreeNode class
class TreeNode{
public:
int val;
TreeNode *left, *right;
// Constructor
TreeNode(int val){
this->val=val;
left=right=NULL;
}
};
// Taking maxLevel initially as -1.
int maxLevel=-1;
// Helper function to print
// left view of a Binary Tree
void leftView_Helper(TreeNode *node, int level){
// Base case i->e-> if node is
// NULL then return
if(node==NULL)
return;
// If the current level is greater than maxLevel so far.
if(level>maxLevel)
{
// Print value of the node->
cout<<node->val<<" ";
// Update maxLevel as level
maxLevel=level;
}
// Call for the left subtree and
// increasing the level by 1.
leftView_Helper(node->left, 1 + level);
// Call for the right subtree and
// increasing the level by 1.
leftView_Helper(node->right, 1 + level);
}
// Wrapper over leftView_Helper
void leftView(TreeNode *root){
// Calling leftView_Helper with
// current level as 0->
leftView_Helper(root, 0);
}
int main(){
/*
Building the following Binary Tree
1
/ \
2 3
/ / \
4 5 6
\ \ \
7 8 9
/
10
*/
TreeNode *root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->right->left = new TreeNode(5);
root->right->right = new TreeNode(6);
root->left->left->right = new TreeNode(7);
root->right->left->right = new TreeNode(8);
root->right->right->right = new TreeNode(9);
root->right->left->right->left = new TreeNode(10);
// Calling the leftView function
leftView(root);
return 0;
}Java
import java.util.*;
public class Main{
// TreeNode class
static class TreeNode{
int val;
TreeNode left, right;
// Constructor
TreeNode(int val){
this.val=val;
left=right=null;
}
}
// Taking maxLevel initially as -1.
static int maxLevel=-1;
// Helper function to print
// left view of a Binary Tree
static void leftView_Helper(TreeNode node, int level){
// Base case i.e. if node is
// null then return
if(node==null)
return;
// If the current level is greater
// than maxLevel so far.
if(level>maxLevel)
{
// Print value of the node.
System.out.print(node.val+" ");
// Update maxLevel as level
maxLevel=level;
}
// Call for the left subtree and
// increasing the level by 1.
leftView_Helper(node.left, 1 + level);
// Call for the right subtree and
// increasing the level by 1.
leftView_Helper(node.right, 1 + level);
}
// Wrapper over leftView_Helper
static void leftView(TreeNode root){
// Calling leftView_Helper with
// current level as 0.
leftView_Helper(root, 0);
}
public static void main(String args[]){
/*
Building the following Binary Tree
1
/ \
2 3
/ / \
4 5 6
\ \ \
7 8 9
/
10
*/
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.right.left = new TreeNode(5);
root.right.right = new TreeNode(6);
root.left.left.right = new TreeNode(7);
root.right.left.right = new TreeNode(8);
root.right.right.right = new TreeNode(9);
root.right.left.right.left = new TreeNode(10);
// Calling the leftView function
leftView(root);
}
}Output:
1 2 4 7 10- Time Complexity – Since we are traversing all the nodes of the tree, time complexity is $O(n)$.
- Space Complexity – $O(n)$, though we don’t use any array or auxiliary data structure, we must consider the recursive stack space used.
Approach-2: Using Level Order Traversal
The concept revolves around identifying and including all nodes in the left view that appear first in their respective levels. An effective strategy is to execute a level order traversal, ensuring the initial node at each level is noted.
To apply this concept, follow these steps:
- Execute a level order traversal across the tree.
- Maintain a record of the traversed level, noting the first node encountered at each level.
- Proceed to the subsequent level.
C/C++
#include <bits/stdc++.h>
using namespace std;
// TreeNode class
class TreeNode {
public:
int val;
TreeNode *left, *right;
// Constructor
TreeNode(int val) {
this->val = val;
left = right = NULL;
}
};
// Function to print the left view of Binary Tree
void leftView(TreeNode *root) {
if (root == NULL) return;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
// Number of nodes at current level
int n = q.size();
// Traverse all nodes of current level
for(int i = 1; i <= n; i++) {
TreeNode* temp = q.front();
q.pop();
// Print the left most element at
// the level
if (i == 1) cout << temp->val << " ";
// Add left node to queue
if (temp->left != NULL)
q.push(temp->left);
// Add right node to queue
if (temp->right != NULL)
q.push(temp->right);
}
}
}
int main() {
// Building the following Binary Tree
// 1
// / \
// 2 3
// / \ / \
// 4 5 6 7
TreeNode *root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
root->right->left = new TreeNode(6);
root->right->right = new TreeNode(7);
// Calling the leftView function
leftView(root);
return 0;
}Java
import java.util.*;
public class Main {
// TreeNode class
static class TreeNode {
int val;
TreeNode left, right;
// Constructor
TreeNode(int val) {
this.val = val;
left = right = null;
}
}
// Function to print the left view of Binary Tree
static void leftView(TreeNode root) {
if (root == null) return;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
// Number of nodes at the current level
int size = queue.size();
// Traverse all nodes of the current level
for (int i = 0; i < size; i++) {
TreeNode current = queue.poll();
// Print the first node (leftmost) of each level
if (i == 0) System.out.print(current.val + " ");
// Add left node to the queue
if (current.left != null) queue.add(current.left);
// Add right node to the queue
if (current.right != null) queue.add(current.right);
}
}
}
public static void main(String args[]) {
/*
Building the following Binary Tree
1
/ \
2 3
/ \ / \
4 5 6 7
*/
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.left = new TreeNode(6);
root.right.right = new TreeNode(7);
// Calling the leftView function
leftView(root);
}
}Output:
1 2 4 - Time Complexity – Since we are traversing all tree nodes, the time complexity is $O(n)$.
- Space Complexity – Since we have used a queue data structure to store the given tree’s left view, the space complexity is $O(n)$.
Approach -3 : Using Queue and a Null Pointer
The solution to this problem involves utilizing a queue and a null pointer to signify the beginning of each level. By placing a null pointer initially and, when encountering one, set a boolean flag to true, indicating that the subsequent element should be considered part of the left view.
Following is the execution based on the outlined strategy:
C/C++
#include <bits/stdc++.h>
using namespace std;
// TreeNode class
class TreeNode {
public:
int val;
TreeNode *left, *right;
// Constructor
TreeNode(int val) {
this->val = val;
left = right = NULL;
}
};
// Function to print the left view of Binary Tree
void leftView(TreeNode *root) {
if (root == NULL) return;
queue<TreeNode*> q;
q.push(root);
q.push(NULL); // Add NULL marker to indicate end of the first level
bool isFirstNode = true; // Flag to check if the node is the first node of the level
while (!q.empty()) {
TreeNode* temp = q.front();
q.pop();
if (temp != NULL) {
if (isFirstNode) {
// Print the first node at this level
cout << temp->val << " ";
isFirstNode = false; // Reset flag for the next level
}
// Add left child to the queue
if (temp->left != NULL)
q.push(temp->left);
// Add right child to the queue
if (temp->right != NULL)
q.push(temp->right);
} else {
// End of the current level
if (!q.empty()) {
// Only add a NULL marker if the queue is not empty to prevent infinite loop
q.push(NULL);
isFirstNode = true; // Reset flag for the new level
}
}
}
}
int main() {
// Building the following Binary Tree
// 1
// / \
// 2 3
// / \ / \
// 4 5 6 7
TreeNode *root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
root->right->left = new TreeNode(6);
root->right->right = new TreeNode(7);
// Calling the leftView function
leftView(root);
return 0;
}Java
import java.util.*;
public class Main {
// TreeNode class
static class TreeNode {
int val;
TreeNode left, right;
// Constructor
TreeNode(int val) {
this.val = val;
left = right = null;
}
}
// Function to print the left view of Binary Tree
static void leftView(TreeNode root) {
if (root == null) return;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
queue.add(null); // Add null marker to indicate end of the first level
boolean isFirstNode = true; // Flag to check if the node is the first node of the level
while (!queue.isEmpty()) {
TreeNode temp = queue.poll();
if (temp != null) {
if (isFirstNode) {
// Print the first node at this level
System.out.print(temp.val + " ");
isFirstNode = false; // Reset flag for the next level
}
// Add left child to the queue
if (temp.left != null)
queue.add(temp.left);
// Add right child to the queue
if (temp.right != null)
queue.add(temp.right);
} else {
// End of the current level
if (!queue.isEmpty()) {
// Only add a null marker if the queue is not empty to prevent infinite loop
queue.add(null);
isFirstNode = true; // Reset flag for the new level
}
}
}
}
public static void main(String args[]) {
/*
Building the following Binary Tree
1
/ \
2 3
/ \ / \
4 5 6 7
*/
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.left = new TreeNode(6);
root.right.right = new TreeNode(7);
// Calling the leftView function
leftView(root);
}
}Output:
1 2 4 - Time Complexity – Since we are traversing all the tree nodes, the time complexity is $O(n)$.
- Space Complexity – $O(n)$, because we have used the queue, which stores the information about the nodes in the tree.
Conclusion
- In this article, we have seen what is meant by the
left view of binary treethrough a detailed example. - We have discussed two recursive approaches to print the
left view of binary tree. Both of them were traversing the tree in preorder fashion. - Also, we have seen an iterative implementation using a queue data structure. In this approach, we were traversing the tree in the level order fashion.