The Principle of Inclusion and Exclusion (PIE) is a fundamental counting tool in combinatorics and probability theory. It adeptly determines the total elements that fulfill one or multiple criteria while eliminating redundancies. By aggregating individual counts and deducting shared elements, PIE ensures accurate outcomes.
For instance, in quantifying individuals who own either a cat or a dog, PIE involves summing cat owners with dog owners and subtracting those with both pets. This methodology is indispensable for intricate probability and combinatorial problems, providing a streamlined approach to prevent overcounting and ensure precision in calculations.
Mathematically we can define the principle of Inclusion and Exclusion as below:
For any two finite sets S1 and S2, which are subsets of a Universal set, then (S1-S2), (S2-S1) and (S1 ∩ S2) are the disjoint sets.
Then
$$
n(S1 ∪ S2) = n(S1) + n(S2) – n(S1 ∩ S2)
$$
For three finite sets A_1 , A_2 and A_3, which are subsets of a Universal set, then
Then
$$
n(S1 U S2 U S3) = n(S1) + n(S2) + n(S3) -n(S1 ∩ S2) – n(S2 ∩ S3) – n(S3 ∩ S1) + n(S1 ∩ S2 ∩ S3)
$$
It is so called as for two sets T, S then we calculate the union, the formula goes as
$$
n (T ∪ S) = n (T) + n (S) – n (T ∩ S)
$$
As we see here we are "INCLUDING" n(T) and n(S) and like wise we are "EXCLUDING" n(T ∪ S).
Basic Set Theory
Before we learn more about the the principle of inclusion and exclusion, let us first cover some basics of set theory which play an important role to understand same.
We can define a set as a collection of correlated elements, such as cat owners, or books in a discrete library section here an element is a member of the set that must be contained in the set.
let us consider an example to grasp the concept better:
Suppose we have a set S, for elements which are contained in this set will be denoted as |S| and this is called as the cardinality of S.
Now suppose we have two such sets S and T.
To find out the union of S and T which will be a set that contains the elements present in either S or T or both, and can be presented as:
$$
S ∪ T
$$
To find out the intersection of S and T which will be a set that contains the elements present in both S and T, and can be presented as:
$$
S ∩ T
$$
To find out the number of elements in the union of the two sets S and T is as below:
$$
|S ∪ T|
$$
To find out the number of elements in the intersection of the two sets S and T is as below:
$$
|S ∩ T|
$$
Finally to define the universe or U we need to consider all the elements present in S or T or even outside of S and T.
Inclusion-Exclusion with Two Sets
Now we shall understand the principle of Inclusion and Exclusion with Two Sets.
Consider two sets S and T , for counting the total elements in the union of two sets (S and T) , we will need to know the number of items in set S and the number of items in set T and then we need to know the number of items in both S and T that is , the intersection of set S and T as shown below.
Now if we keep adding the elements in both sets S and T together , we shall be counting the elements in the intersection part twice and hence we need to avoid it. With that being said we need to subtract the intersection of S and T to obtain the correct number of elements in the union of S and T.
We can mathematically put this as:
$$
|S ∪ T| = |S| + |T| – |S ∩ T|
$$
For visualizing this concept we shall be using the Venn diagram to analyse the visual representation of sets.
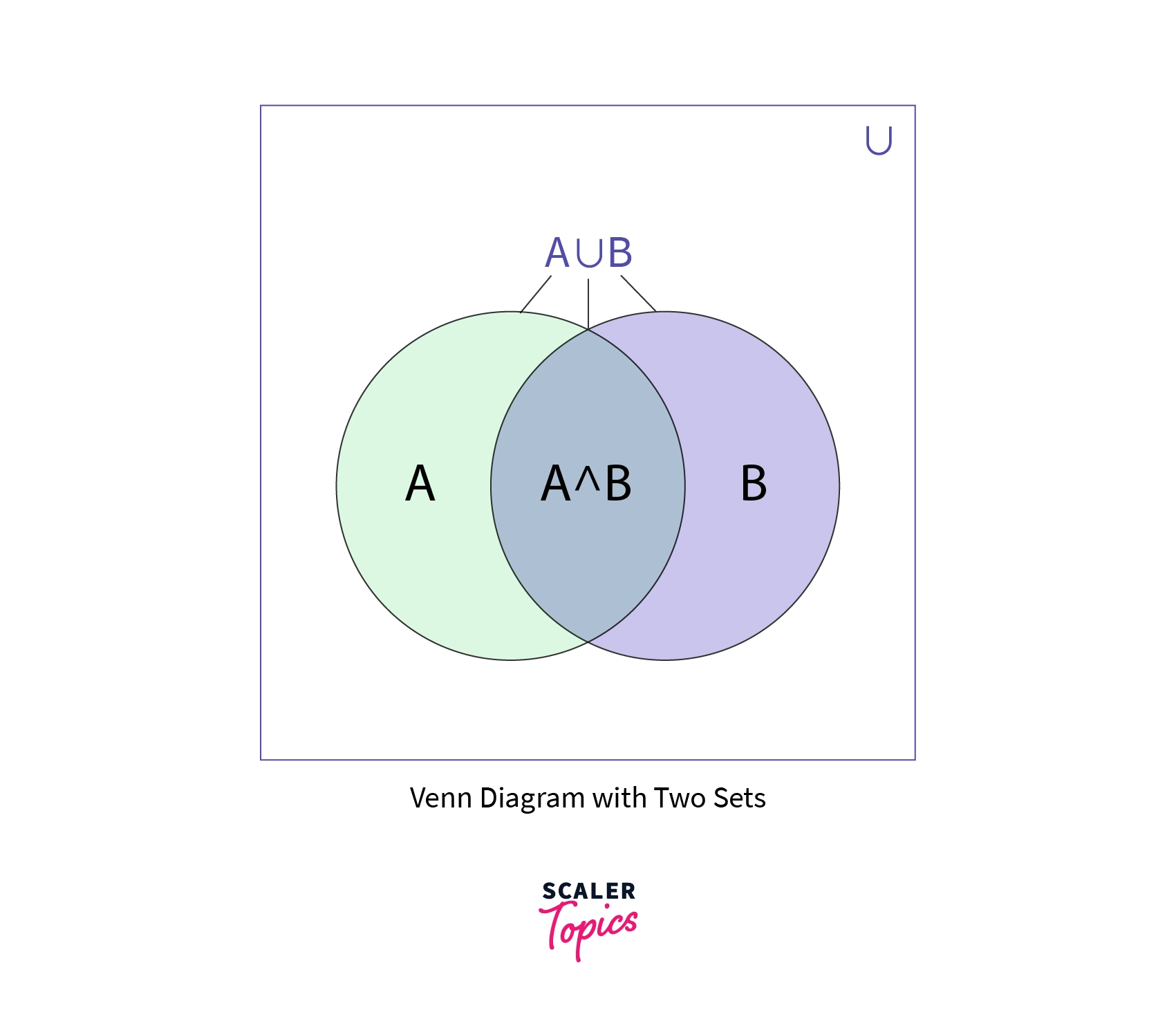
As we see below, the left circle is set S and the right circle is set T, and the middle overlaped part is the intersection of S and T.
Now to understand the union of these two sets all the elements that are contained within circle S or circle T represents the union. Now as we understood from above, as the intersection is contained for both circles which is twice, we must subtract in order to count it once. Also, the entire box represents the universe U that is, everything which lies in the box is a part of universe.
Venn Diagram with Two Sets:
Examples with Two Sets
Let us dive deep into the example to understand better the union of two sets and broden the understanding of the principle of inclusion and exclusion for same. Consider a group of students out of which 15 study Physics, 8 study Chemistry and the common number of students who study both are 5.Now we have to calculate how many students study either (Physics or Chemistry) or both.
Lets us use P for Physics and C for Chemistry, we get the following formula:
$$
|P ∪ C| = |P| + |C| – |P ∩ C|
$$
Now let us plug the values given as part of the problem statement:
$$
|P ∪ C| = |15| + |8| – |5|
$$
$$
|P ∪ C| = |18|
$$
There are 18 students that study either Physics or Chemistry or both.
Now let us understand the concept where we shall calculate the number of elements that are not in a certain set.
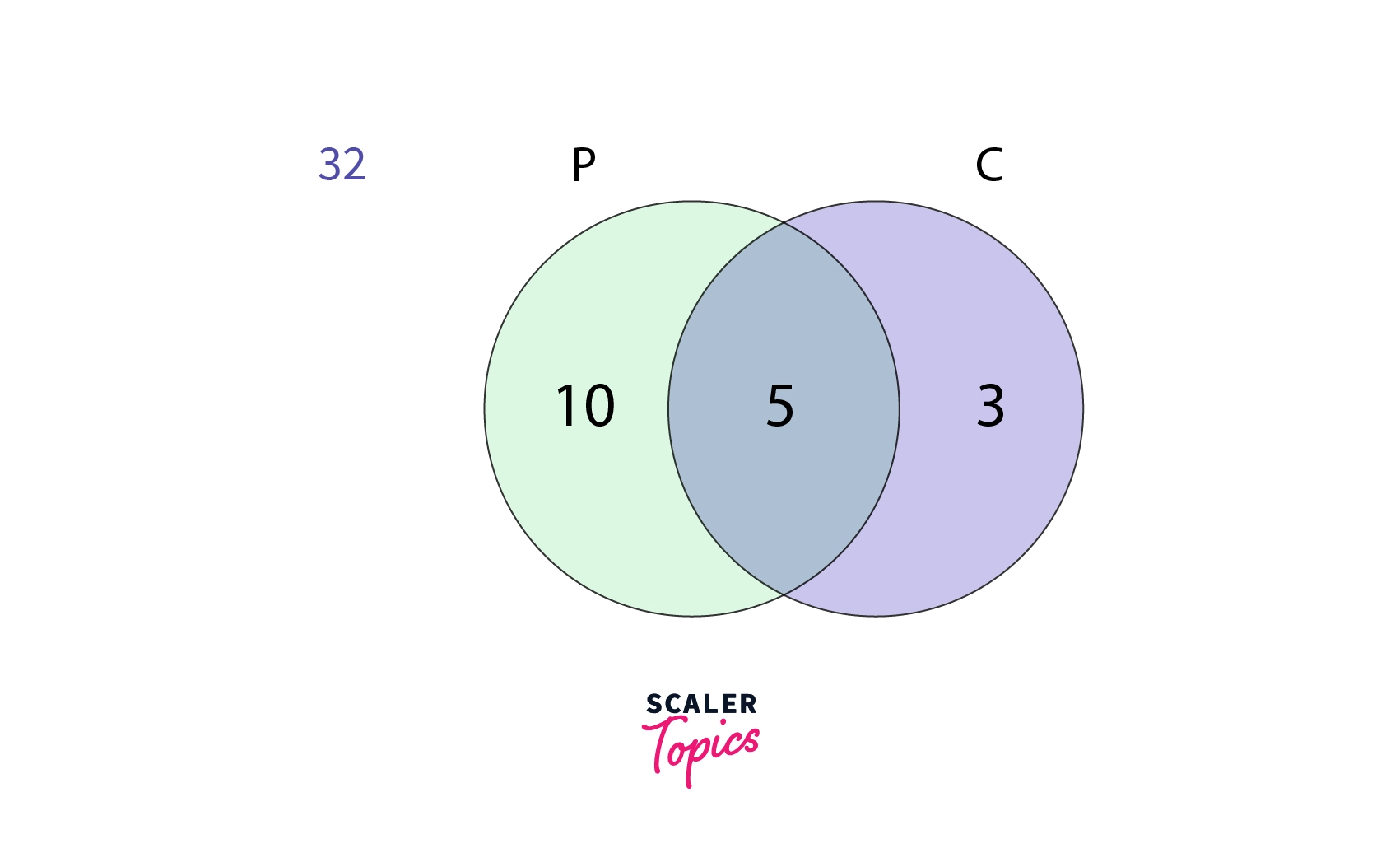
Suppose we had total of 50 students out of which 15 study Physics, 8 study Chemistry and the common number of students who study both are 5.
Then as per above we have 18 students that study either Physics or Chemistry or both.
Now we shall subtract 18 from 50 to obtain the number of students that is, 32 are the students who study neither of the both and are said to be outside the union and inside the entire box as can be seen below.
Inclusion-Exclusion with Three Sets
Now we shall understand the principle of Inclusion and Exclusion with Three Sets.
Consider two sets S1, S2 and S3 , for counting the total elements in the union of three sets (S1, S2 and S3) , we will need to know the number of items in set S1, the number of items in set S2, the number of items in set S3 and then we need to know the number of items in all the three sets S1, S2 and S3 (overlapping of all the three sets) as can be seen below.
Now we shall observe that if we keep adding the elements in all the three sets S1, S2 and S3 , we shall be counting the elements in the intersection part of the three sets for all sets S1, S2 and S3 which will lead to addition of elements incorrectly. With that being said we will need to subtract the intersection of (S1 and S2), (S2 and S3) and ( S3 and S1) to obtain the correct number of elements in the union of S1, S2 and T.
We can mathematically put this as:
$$
|S1 U S2 U S3| = |S1| + |S2| + |S3| – |S1 ∩ S2| – |S2 ∩ S3| – |S3 ∩ S1| + |S1 ∩ S2 ∩ S3|
$$
For visualizing this concept we shall be using the Venn diagram to analyse the visual representation of sets.
As we see below, the three circles S1, S2 and S3 are all intersected by one another. The middle overlaped part is the intersection of S1, S2 and S3. And we can also see that the two sets are intersecating as well three times for the three sets S1, S2 and S3.
Now to understand the union of these three sets all the elements that are contained within circle S1, S2 or circle S3 represents the union. Now as we understood from above, the intersection for two circles are happening thrice and we must subtract in order to count the elements once. Also, the entire box represents the universe U that is, everything which lies in the box is a part of universe.
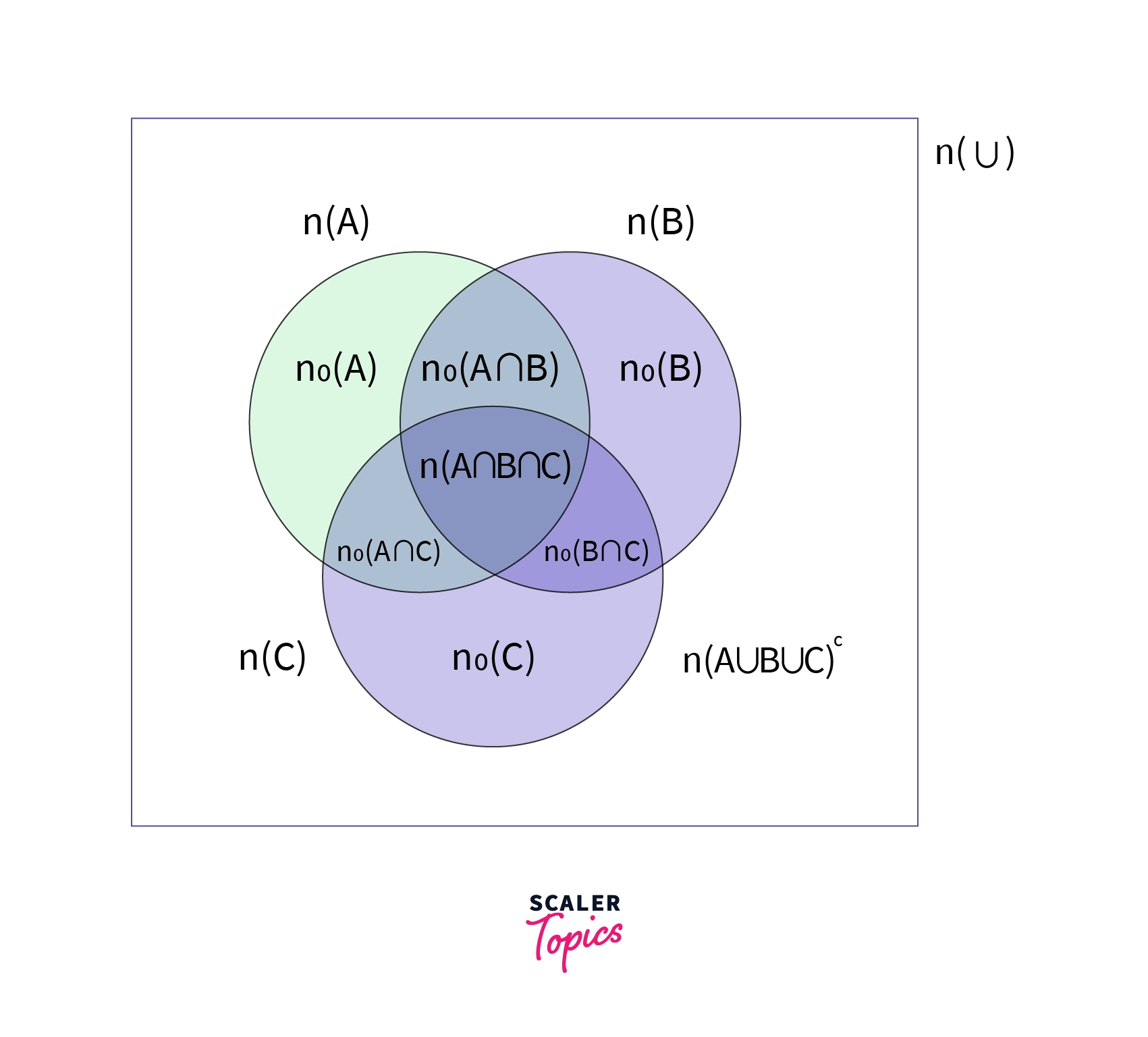
Venn Diagram with Three Sets:
Examples with Three Sets
Let us dive deep into the example to understand better the union of three sets and broden the understanding of the principle of inclusion and exclusion for same. Consider a group of students out of which 15 study Physics, 11 study Chemistry and 13 study English. The number of students who study all three are 4. The number of students who study both Physics and Chemistry are 6, The number of students who study both English and Physics are 8 and The number of students who study both English and Chemistry are 7.
Considering the above scenario we need to find out how many students study either (Physics or Chemistry or English) or all.
Lets us use P for Physics and C for Chemistry and E for English, we get the following formula:
$$
|P U C U E| = |P| + |C| + |E| – |P ∩ C| – |C ∩ E| – |E ∩ P| + |P ∩ C ∩ E|
$$
Now let us plug the values given as part of the problem statement:
$$
|P U C U E| = |15| + |11| + |13| – |6| – |7| – |8| + |4|
$$
$$
|P ∪ C| = |22|
$$
There are 22 students that study either Physics or Chemistry or English or all three.
Now let us understand the concept where we shall calculate the number of elements that are not in a certain set.
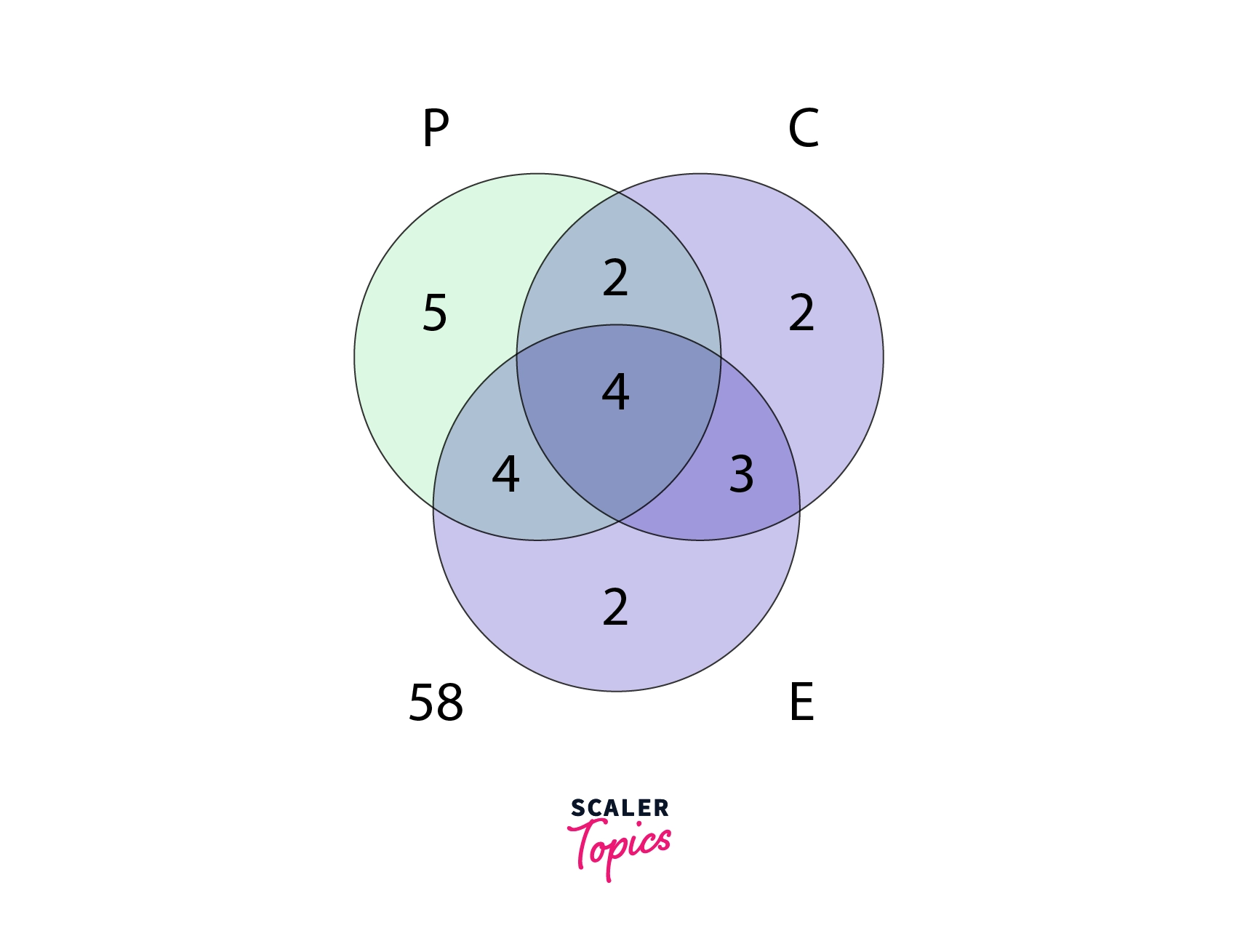
Suppose we had total of 80 students out of which 15 study Physics, 11 study Chemistry and 13 study English as mentioned above.
Then as per above we have 22 students that study either Physics or or English or all three.
Now we shall subtract 22 from 80 to obtain the number of students that is, 58 are the students who study neither of the three subjects and are said to be outside the union and inside the entire box as can be seen below.
Principle of Inclusion-Exclusion
Below we shall be understanding the Principle of Inclusion and Exclusion:
Suppose we have random number finite sets like S1, S2, S3 … Sn, then the union of this set can be found out by ->
Sum of sizes of all the single sets – Sum of all 2-set intersections + Sum of all the 3-set intersections – Sum of all 4-set intersections .. + (-1)^{n+1} Sum of all the n-set intersections.
Mathematically it can be represented as below:
$$
|A1\cup A2\cup A3…\cup Ai| = \sum_{1<k<i}|Ak| + (-1)\sum_{1<k1<k2<i}|Ak1\cap Ak2| +(-1)^2\sum_{1<k1<k2<k3<i}|Ak1\cap Ak2\cap Ak3| + (-1)^i+1\sum_{1<k1<k2<k3…<ki<i}|Ak1\cap Ak2\cap Ak3….\cap Aki|
$$
Properties of Inclusion-Exclusion
The properties that defines the Inclusion-Exclusion concepts are as below:
Helps to find the total number of elements.Easier approach to avoid the double counting problems.
Conclusion
- The
principle of Inclusion-Exclusionis an effective way to calculate the size of the individual set related to its union. - It is so called as for two sets
T, Sthen we calculate the union, the formula goes as
$$
n (T ∪ S) = n (T) + n (S) – n (T ∩ S)
$$
As we see here we are “INCLUDING“ n (T) and n (S) and like wise we are “EXCLUDING“n(T ∪ S). - The union of sets
SandTcan be presented asS ∪ Tand the number of elements in the union can be given by|S ∪ T| - The intersection of sets
SandTcan be presented asS ∩ Tand the number of elements in the union can be given by|S ∩ T| - The principle of
inclusion and exclusionprinciple is mathematically represented as :
Sum of sizes of all the single sets – Sum of all 2-set intersections + Sum of all the 3-set intersections – Sum of all 4-set intersections .. + (-1)^{n+1}Sum of all the n-set intersections. - The properties that defines the Inclusion-Exclusion concepts are as below:
a. Helps to find the total number of elements.
B. Easier approach to avoid the double counting problems.
- The Union for Two sets are given by:
$$
|S ∪ T| = |S| + |T| – |S ∩ T|
$$ - The Union for Three sets are given by:
$$
|S1 U S2 U S3| = |S1| + |S2| + |S3| – |S1 ∩ S2| – |S2 ∩ S3| – |S3 ∩ S1| + |S1 ∩ S2 ∩ S3|
$$