Prim’s Algorithm offers a strategic approach to constructing a minimum spanning tree from a given graph, ensuring every vertex is connected with the least total edge weight. This efficient method begins with a single vertex, expanding by selecting the lowest weight edges connecting to unvisited nodes, thus weaving a path that covers all without excess.
Let us try to break down this definition by understanding each word.
Terminologies
Graph: A collection of nodes and edges. You can think of nodes as cities and edges as the roads connecting the cities.
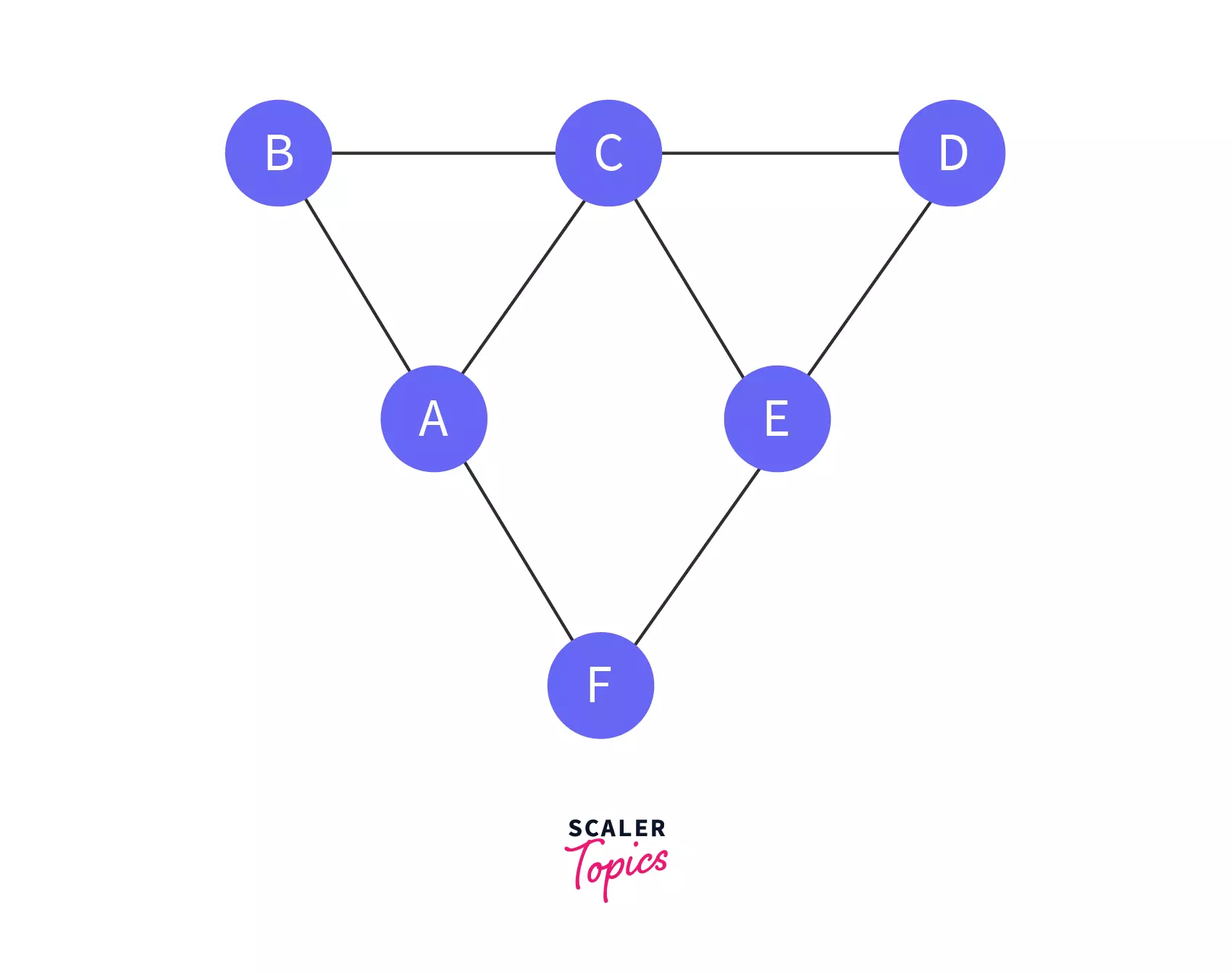
Tree: A tree is a graph without cycles. A cycle is formed when there is more than one way to reach from one city to another.
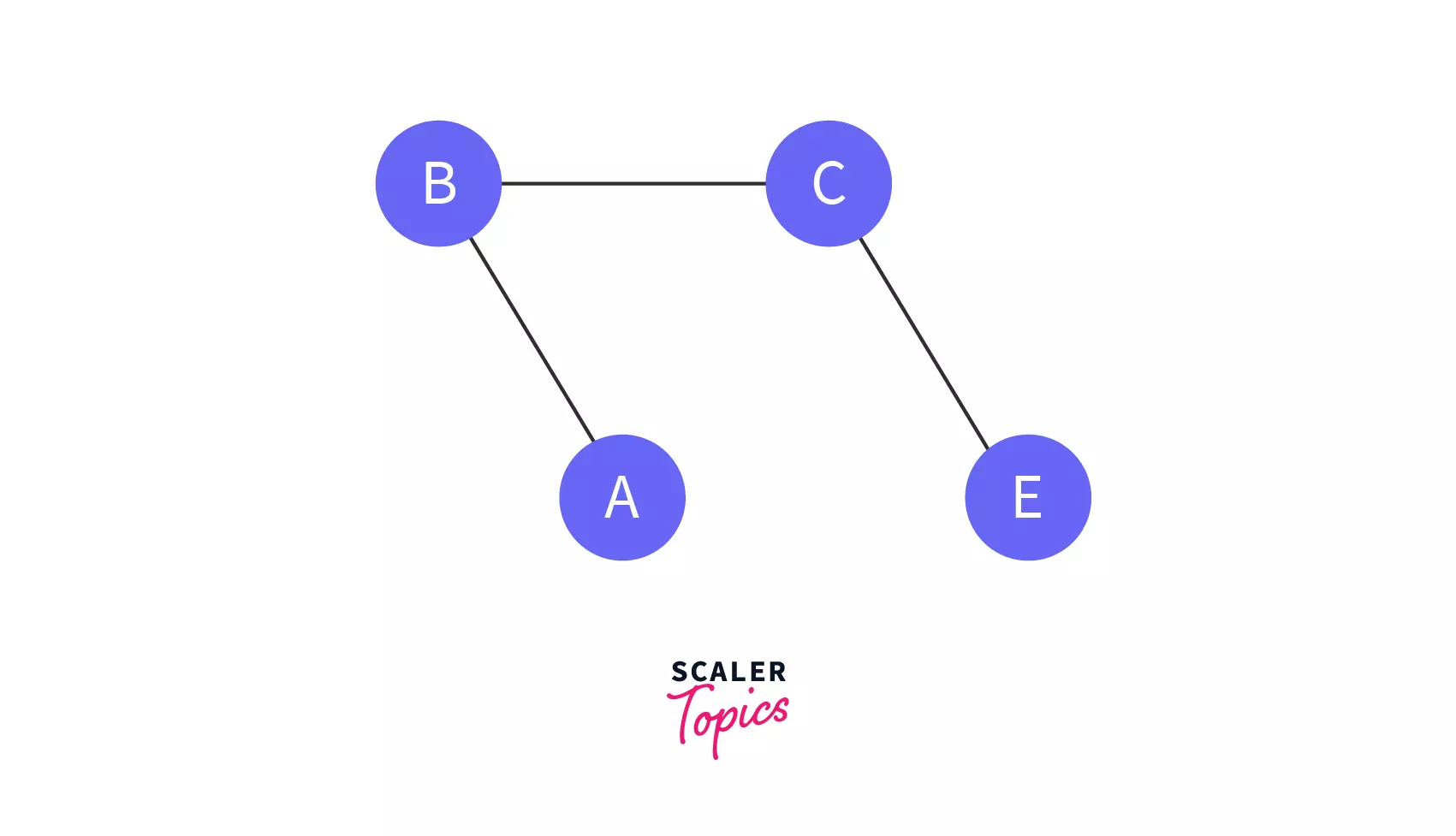
Weighted graph: Weighted graph is a graph with a value associated with each of its edges. This value is called theweight of that edge.
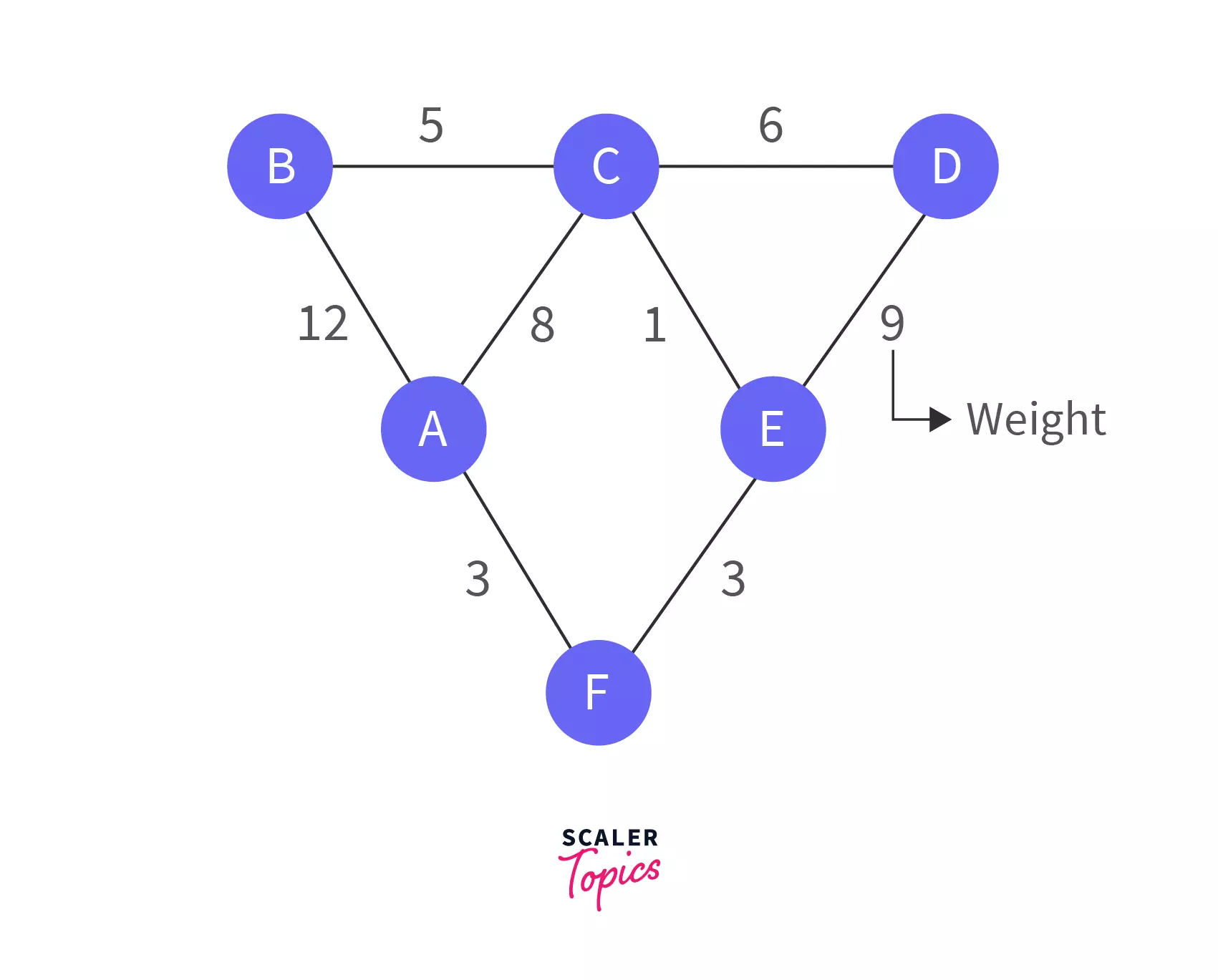
Spanning Tree: Spanning tree of a graph is a tree that includes all the vertices. There are roads that connect every city. Below are some of the possible spanning trees
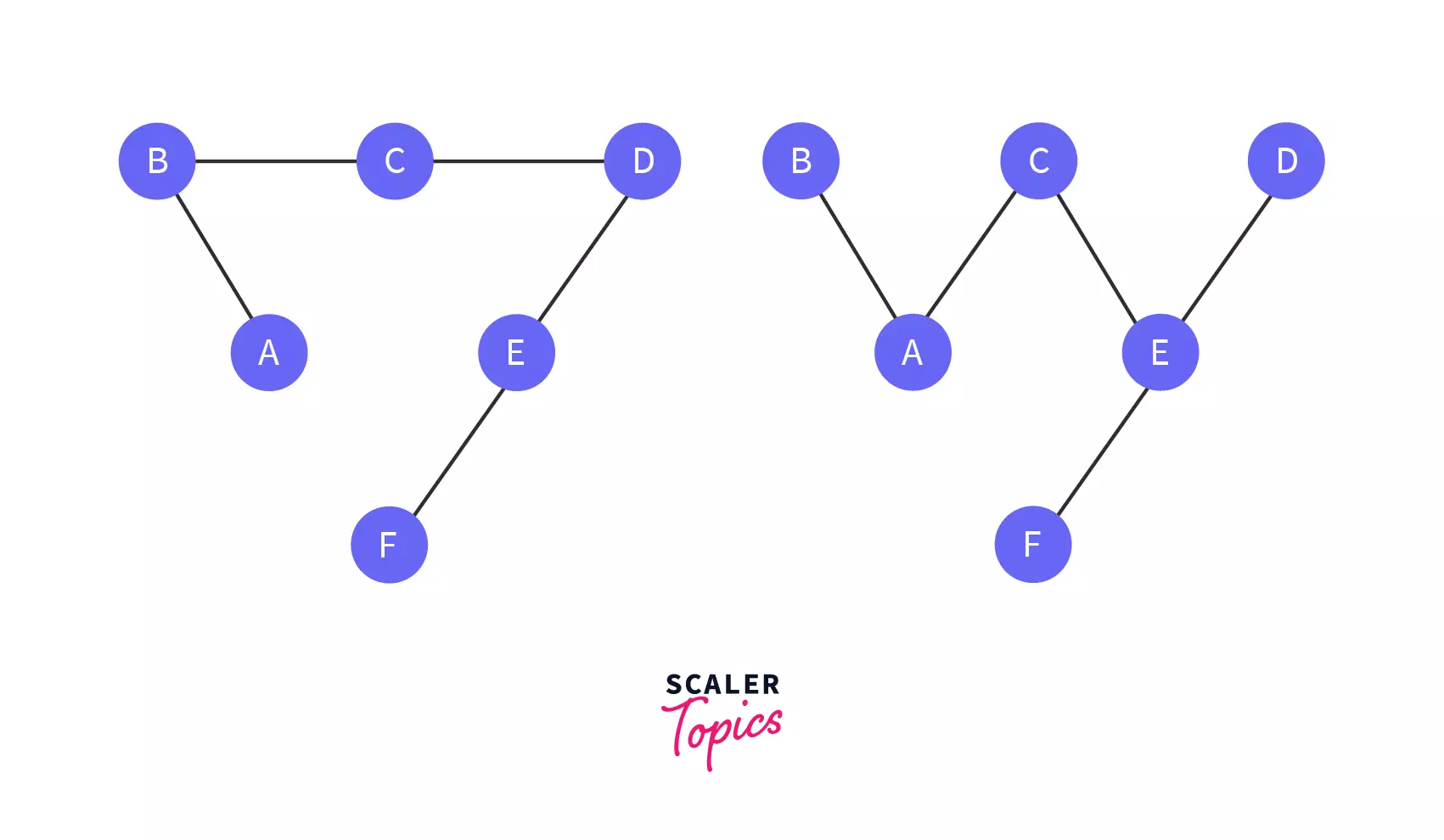
Minimum Spanning Tree: Minimum Spanning Tree of a weighted graph is a spanning tree such that the sum of all the weights of the spanning tree is minimum. Of all the possible spanning trees we pick the one with minimum weight sum as shown below:
How Prim’s Algorithm works?
Prim’s algorithm builds a minimum spanning tree (MST) by adding vertices from a starting vertex. It follows these steps:
- Initialize MST: Begins with a single vertex from the graph.
- Find Minimum Edge: Selects the least weight edge connecting the MST to another vertex.
- Update Edges: Modifies the edge set to avoid cycles by including new edges from the MST and excluding any that form loops.
- Complete MST: Continues until all vertices are incorporated, each time adding the smallest edge to expand the MST without forming cycles.
Prim’s Algorithm Implementation
Prims Algorithm belongs to the Greedy class of algorithms. This simply means that at every step, the algorithm will make a decision depending on what is the best choice at that point.
In other words at each step, it solves the current problem in the best way and assumes the complete problem will be solved eventually in the best way.
Let’s take a look at the steps of the algorithm:
- Start with a random vertex in the graph and mark it as visited
- Iterate over all the visited vertices and pick the minimum weight edge that is not yet processed
- Keep repeating step
2until all the nodes are visited.
The below graphic shows Prims algorithm in action. The blue line at each step is the smallest edge of all the edges connected to the current set of vertices.
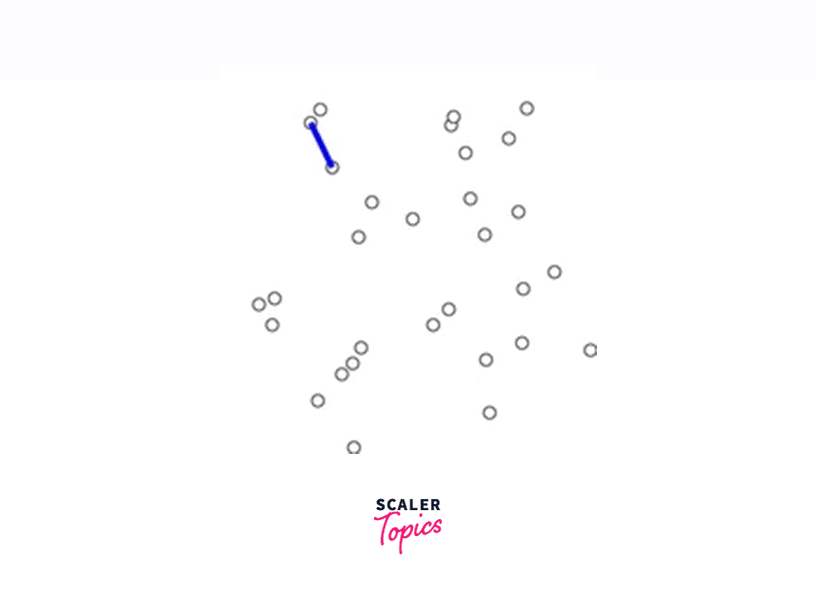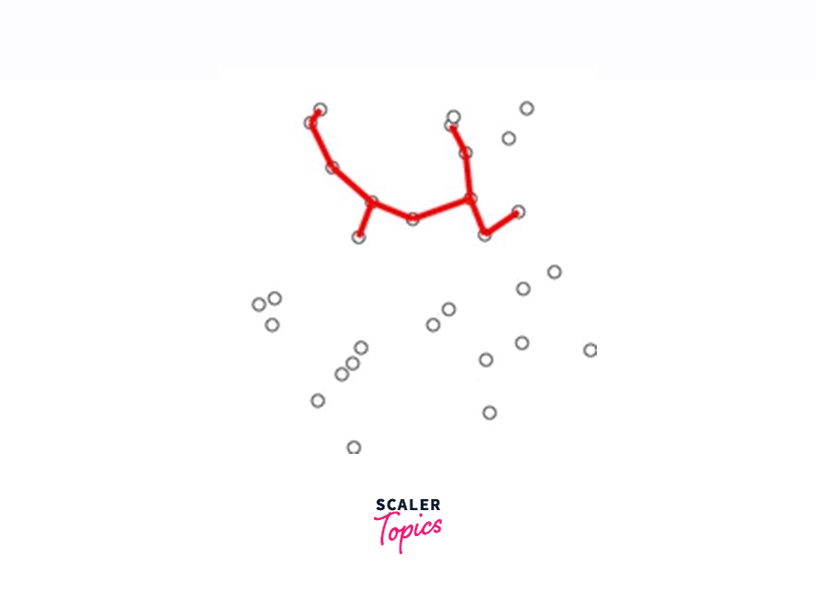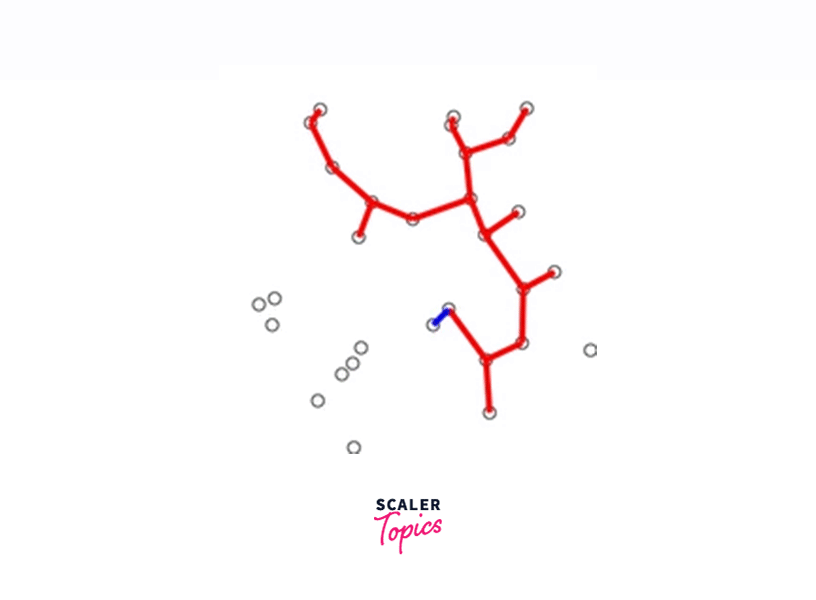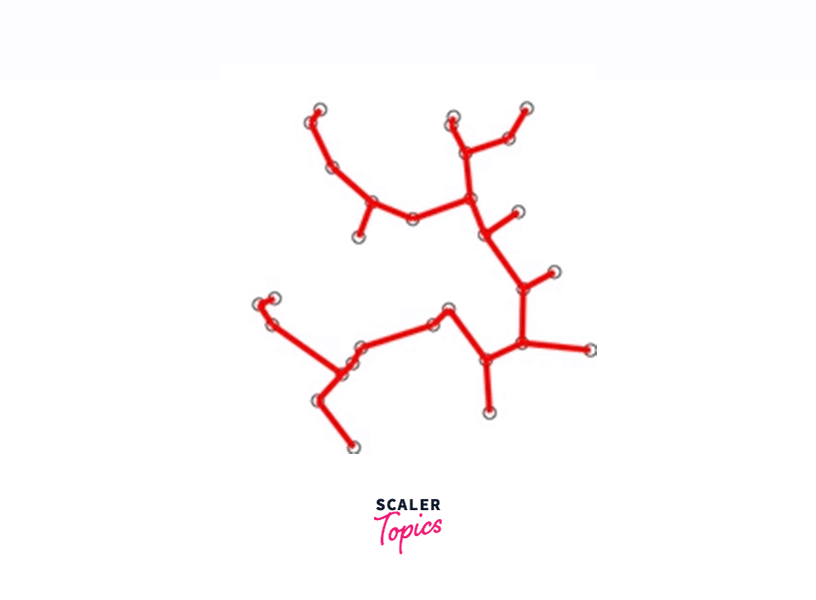
Prim’s Algorithm Example
Let’s see a step-by-step walkthrough of the algorithm:
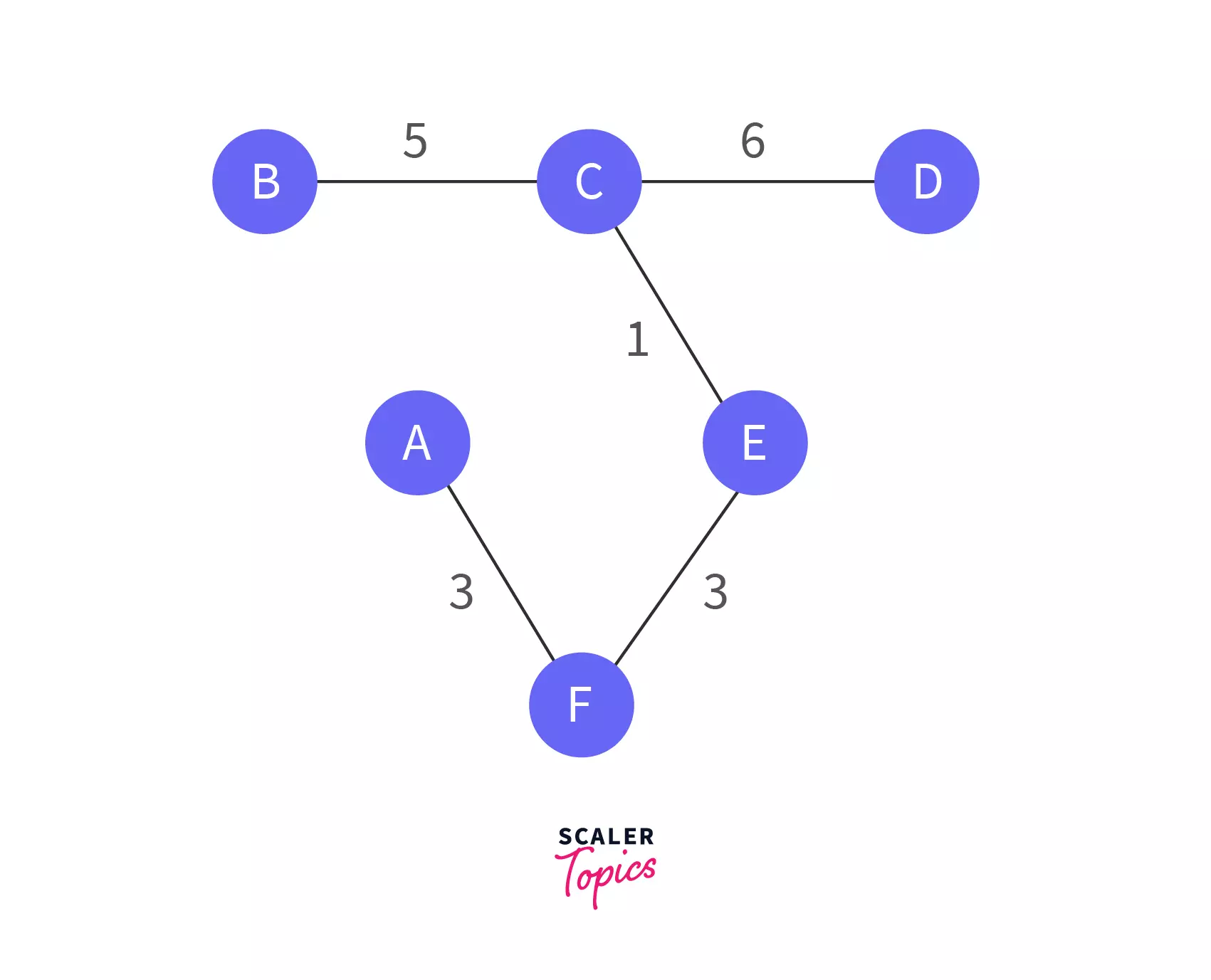
Consider the below table with all source and destination vertices along with their weights. We want to find the minimum spanning tree for this graph.
| Source | Destination | Weight |
|---|---|---|
C (2) | E (4) | 1 |
A (0) | F (5) | 3 |
E (4) | F (5) | 3 |
B (1) | C (2) | 5 |
C (2) | D (3) | 6 |
A (0) | C (2) | 8 |
D (3) | E (4) | 9 |
A (0) | B (1) | 12 |
We can represent this table in the form of a diagram as shown in the first figure below:
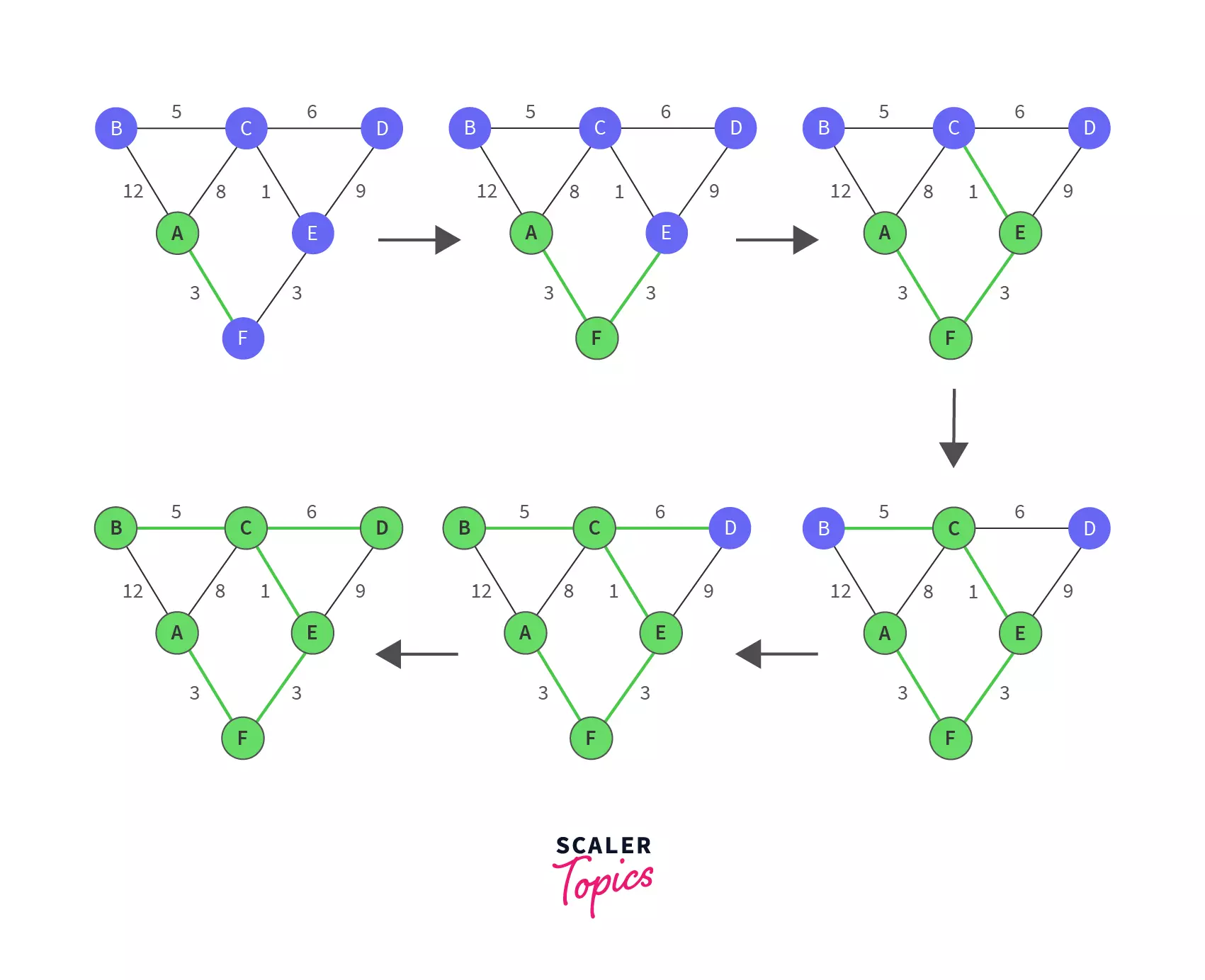
Figure-1: We pick a random vertex (A in our case). The smallest edge from A is AF having a weight of 3.
Figure-2: Now A and F are the vertices in our answer set. The edges for these vertices which are not yet selected are (AB, AC, and FE). Of these FE has the smallest weight of 3.
Figure-3: Now the answer set has A, F, and E. Among the edges connected to all these vertices, EC has the next minimum cost.
Figure-4: Vertices A, F, E, and C are visited. The not selected edges for these vertices are CB, CA, AB, CD, ED. Of these, edge CB has the minimum cost.
Figure-5: The next minimum cost edge is CD.
Figure-6: We stop the algorithm as all the vertices are visited.
Java and C++ Example of Prim’s Algorithm
1. Java
import java.io.*;
import java.lang.*;
import java.util.*;
public class Solution{
//selects the vertex which has the least weight edge of all unselected vertices.
static int selectMinVertex(int[] value, boolean[] setMST){
int minimum = Integer.MAX_VALUE;
int vertex = 0;
for(int i = 0; i < value.length; i++){
if(setMST[i] == false && value[i] < minimum) {
vertex = i;
minimum = value[i];
}
}
return vertex;
}
//Print the minimum spanning tree
static void printMst(int[] parent, int[][] graph){
System.out.println("Src.\tDest.\tWeight\n");
for(int i = 1; i < parent.length; i++){
System.out.println(i + "\t" + parent[i] + "\t" + graph[i][parent[i]] + "\n");
}
}
static void findMST(int graph[][]){
int V = graph.length;
int[] parent = new int[V];
int[] value = new int[V];
boolean[] setMST = new boolean[V];
for(int i = 0; i < V; i++){
value[i] = Integer.MAX_VALUE;
}
parent[0] = -1;
value[0] = 0;
//Iterate through all the vertices of the graph
for(int i = 0; i < V-1; i++){
/**
* From all vertices connecting the currently chosen vertices,
* select a vertex that adds minimum edge
**/
int U = selectMinVertex(value, setMST);
setMST[U] = true;
/**
* Add newly added vertex as the parent of all the vertices
* it connects to except those that are already chosen.
* This would help us print the tree later.
**/
for(int j = 0; j < V; j++){
if(graph[U][j] != 0 && setMST[j] == false && graph[U][j] < value[j]){
value[j] = graph[U][j];
parent[j] = U;
}
}
}
printMst(parent, graph);
}
public static void main(String[] args) {
/**
* This is the adjacency matrix representation of graph where
* the weight for the edge i,i is stored in ith row and jth column
* **/
int[][] graph = {
{0, 4, 6, 0, 0, 0},
{4, 0, 6, 3, 4, 0},
{6, 6, 0, 1, 8, 0},
{0, 3, 1, 0, 2, 3},
{0, 4, 8, 2, 0, 7},
{0, 0, 0, 3, 7, 0},
};
findMST(graph);
}
}2. C++
#include<bits/stdc++.h>
using namespace std;
#define V 6
//Selects the vertex which has the least weight edge of all unselected vertices.
int selectMinVertex(vector<int> &value, vector<bool>& setMST){
int minimum = INT_MAX;
int vertex;
for(int i = 0; i < V; i++){
if(setMST[i] == false && value[i] < minimum){
vertex = i;
minimum = value[i];
}
}
return vertex;
}
//Print the minimum spanning tree
void printMst(int[] parent, int graph[V][V]){
cout << "Src.\tDest.\tWeight\n";
for(int i = 1; i < parent.length; i++){
cout << i << "\t" << parent[i] << "\t" << graph[i][parent[i]] << "\n";
}
}
void findMST(int graph[V][V]){
int parent[V];
vector<int> value(V, INT_MAX);
vector<bool> setMST(V, false);
parent[0] = -1;
value[0] = 0;
//Iterate through all the vertices of the graph
for(int i = 0; i < V-1; i++){
/** from all vertices connecting the currently chosen vertices,
* select a vertex which adds minimum edge
**/
int U = selectMinVertex(value, setMST);
setMST[U] = true;
/**
* Add newly added vertex as parent of all the vertices
* it connects to except those that are already chosen.
* This would help us print the tree later.
**/
for(int j = 0; j < V; j++){
if(graph[U][j] != 0 && setMST[j] == false && graph[U][j] < value[j]){
value[j] = graph[U][j];
parent[j] = U;
}
}
}
printMst(parent, graph);
}
int main(){
/**
* This is the adjacency matrix representation of graph where
* the weight for the edge i,i is stored in ith row and jth column
* **/
int graph[V][V] = {
{0, 4, 6, 0, 0, 0},
{4, 0, 6, 3, 4, 0},
{6, 6, 0, 1, 8, 0},
{0, 3, 1, 0, 2, 3},
{0, 4, 8, 2, 0, 7},
{0, 0, 0, 3, 7, 0},
};
findMST(graph);
return 0;
}Complexity Analysis of Prim’s Algorithm
Time Complexity
The time complexity of Prim’s Algorithm primarily depends on the data structure used. With an adjacency matrix, it stands at O(V^2), but employing a binary heap with an adjacency list reduces it to (O(E *log V)). A Fibonacci heap, despite its complex nature, can further optimize this to O(E + V *log V), enhancing efficiency in selecting the minimum weight vertex during each step of the algorithm.
Space Complexity
The space complexity of Prim’s algorithm is O(V), where V is the number of vertices in the graph.
Difference between Prim’s and Kruskal Algorithm
Both Prim and Kruskal follow the greedy approach. The difference is, Prim's greedily chooses vertices while Krushkal's greedily chooses edges.
In Kruskal, we sort through the edges first so that we can select them later one by one from minimum to maximum. This sorting is a costly operation.
Prim's on the other hand goes vertex by vertex only considering edges with minimum cost. So Prim’s does not have to worry even if the number of edges increases as it is never going to process every edge.
Hence, Prims Algorithm is better than Kruskal’s when the graph is dense. i.e. the number of edges is close to the maximal number of edges possible.
Applications of Prim’s Algorithm
- Maze generation: For a randomly weighted graph prims algorithm can be used to generate a maze. Any two nodes can act as the entry and exit nodes of the maze.
- Cable laying, electric grids layout, LAN networks, especially cases where the graphs are dense – In these cases, we need to find connect all the nodes while ensuring the minimum amount of cable is being used exactly the problem statement for Prim’s algorithm.
Prim’s Mantra
Keep the best(minimum cost) edge for every vertex.
Become a master of data structures with our Data Structures in C++ Certification Course. Start your journey today!
Conclusion
- Prim’s Algorithm efficiently constructs a minimum spanning tree, ensuring connectivity with minimal edge weight.
- It employs a greedy approach, progressively adding the lowest weight edges, optimizing for minimal total weight.
- The algorithm’s efficiency varies with data structure choice; using a binary or Fibonacci heap can significantly reduce time complexity.
- Prim’s Algorithm proves superior for dense graphs, offering an optimal solution for scenarios like network design and maze generation.