Persistent Segment Tree

A persistent data structure is a data structure that can retain its past forms when an update operation is applied to it. A Persistent Segment Tree is used when we want to implement persistency in a Segment Tree. A persistent segment tree can can preserve its past states and can handle updates at the same time. Persistent data structures are used in version controls like Git and others which enables multiple users to make branches from the current version and make changes without affecting the older versions.

Scope of article

• This article defines a Persistent Segment Tree and explains the intuitive logic behind this data structure.
• The article also shows the C++ implementation for solving range sum queries while handling point updates using a Persistent Segment Tree.

Takeaways

• In Persistent Segment Tree, the time complexity of
  • Update – $O(log N)$
  • Range query – $O(log N)$
• Persistent Segment Tree is used when we want to store the previous results as well as handle point updates and answer range queries on the segment tree after the Kth update efficiently.

Introduction

A Segment tree is a highly versatile and efficient data structure used to solve problems involving range queries and is flexible enough to handle update queries over a range as well as point update queries in $O(log N)$ time complexity. We would recommend everyone to refer to the article Segment Tree, as a prerequisite to this article where we discussed how we can use a Segment Tree to handle point updates. In this post, we will see how we can introduce persistency in a segment tree.

Let us suppose you have a segment tree, say SegmentTree1. After performing an update query in SegmentTree1 the segment tree changes, say becomes SegmentTree2.

If we use a simple segment tree then we will lose the data present in the SegmentTree1. Hence, there will be no way for us to perform any query in SegmentTree1 after the update operation. Thus we need to use a persistent data structure to solve the problem as we need to preserve the past states after the update operations.

We can use a Persistent Segment Tree to solve the given problem in an efficient way. Let us discuss how we can implement persistency in a Segment Tree and the basic idea behind it.

Basic Idea Behind a Persistent Segment Tree

Since we want to preserve the previous state after each update operation we can build a new version of the segment tree each time an update operation is performed.

We can store all the previous versions of the Segment Tree in a two-dimensional array or in a vector of vectors depending on whether we have used an array or a vector to build the Segment Tree.

However, as the build query takes $O(N)$ time and space complexity. Thus, if there are Q update queries it will take $O(Q*N)$ time and space complexity to get performed. We can use a persistent segment to solve the problem much efficiently where each update operation can be done in $O(log N)$ time and space complexity. Let us see how we can implement the same.

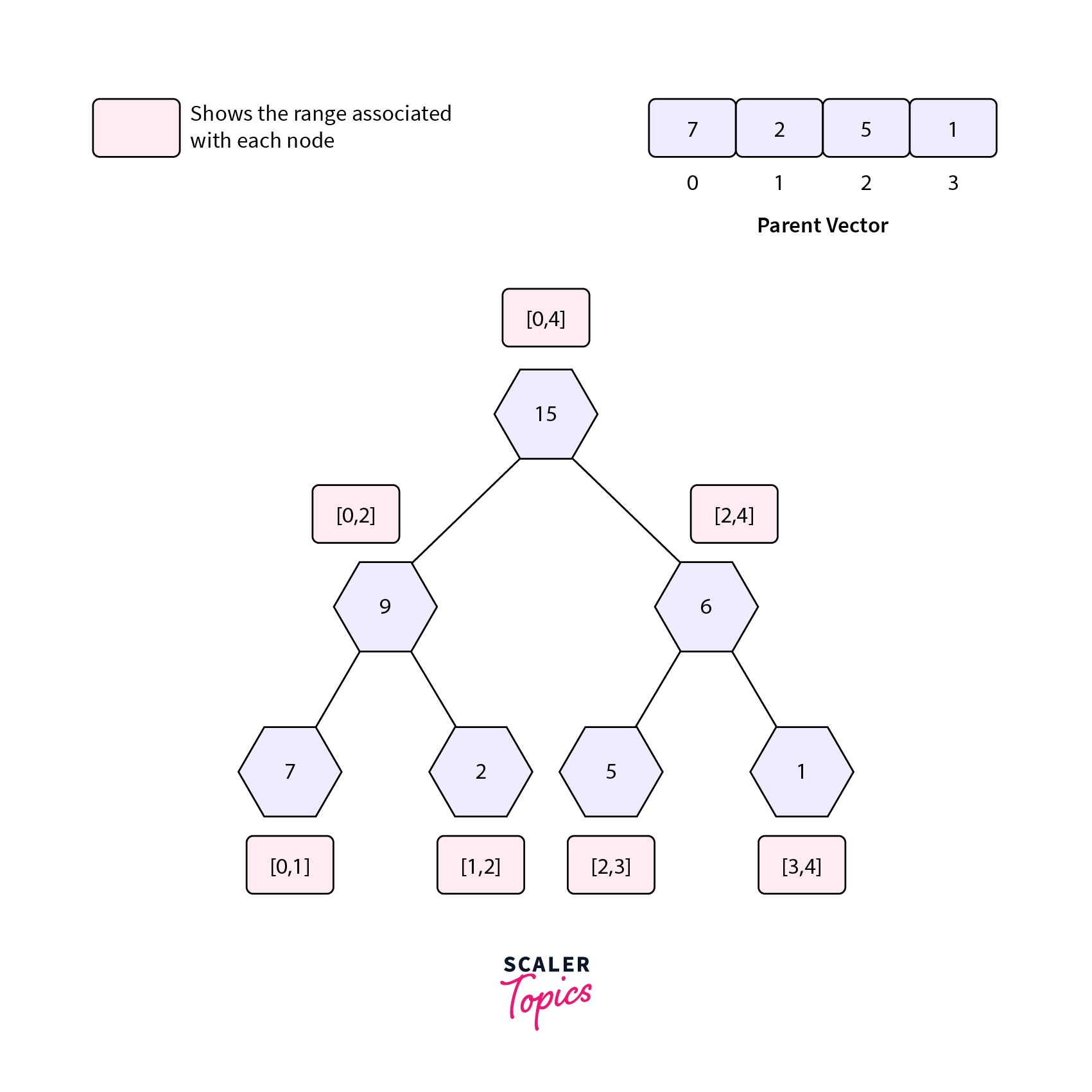
Consider the segment tree used for range sum queries shown below,

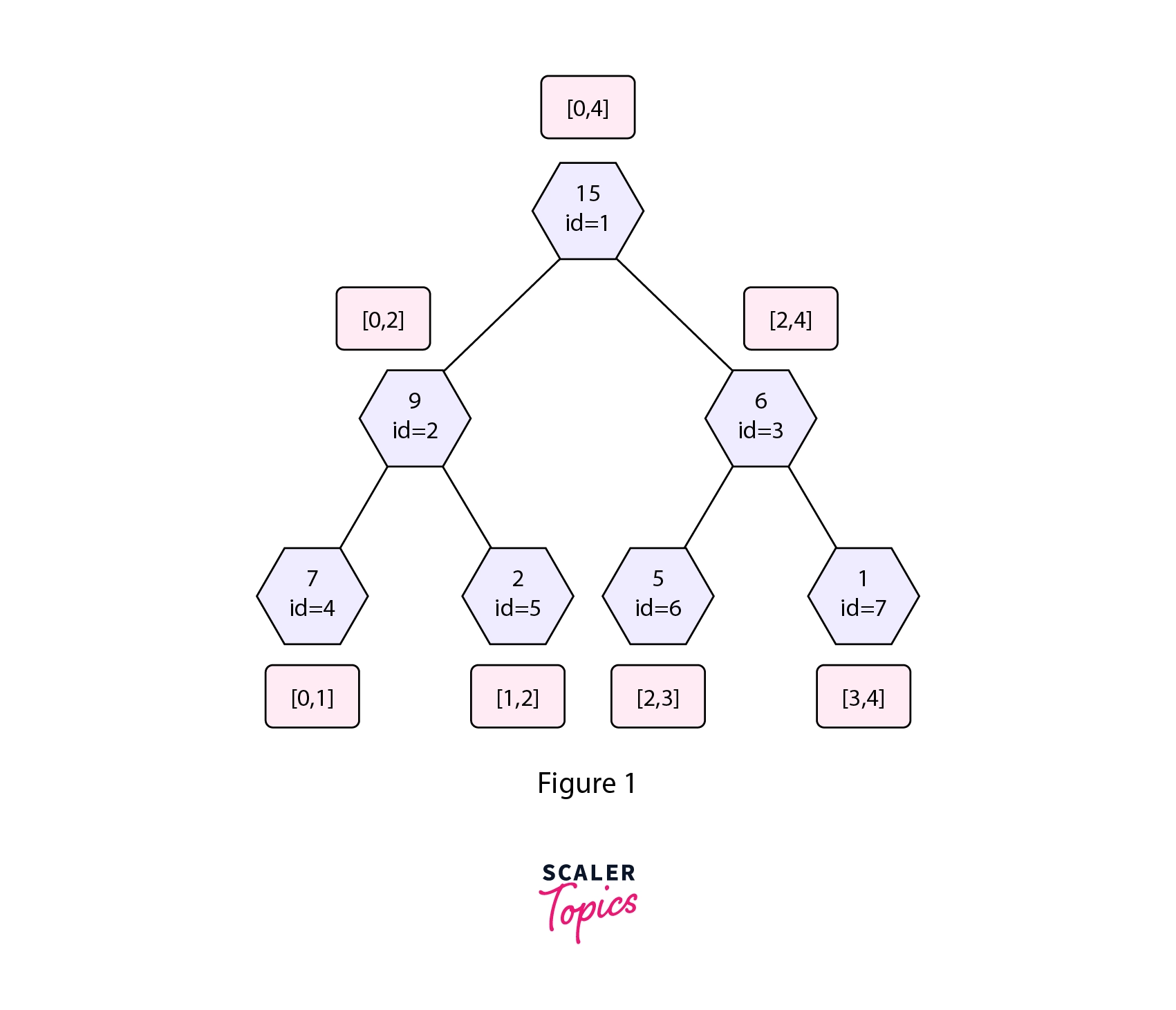
The diagram above shows the structure of a simple segment tree used to find the sum in given range queries.

• Each node stores the sum of a particular interval of the parent array (the array from which the segment tree is built).
• The id associated with each node helps to uniquely identify a particular node in the simple segment tree.
• The leaf nodes represent a particular element from the parent array.
• The blue boxes represent the interval associated with a given node (left range as inclusive and right range as exclusive). The range [LeftRange, RightRange) is same as [LeftRange,RightRange-1].

Say, we want to update the value present in the 3rd index of the original array to value=3 (0 based indexing). Let’s briefly discuss the approach we use to solve the point update operation in a Simple Segment Tree.

In the Segment Tree shown in figure 1 the node with id=7 represents the node to be updated in the given update operation. Thus we make a dfs call from the root node to the node with id=7 in the Segment Tree. We update the value present in the Segment Tree and also update the value present in the parent array.

While backtracking we update all the nodes in the path from the root node to that leaf node in the Segment Tree. In the given update operation nodes with id=1,3,7 will get affected by the given update operation as the interval we updated falls completely inside the interval associated with these nodes. Refer to the diagram shown below.

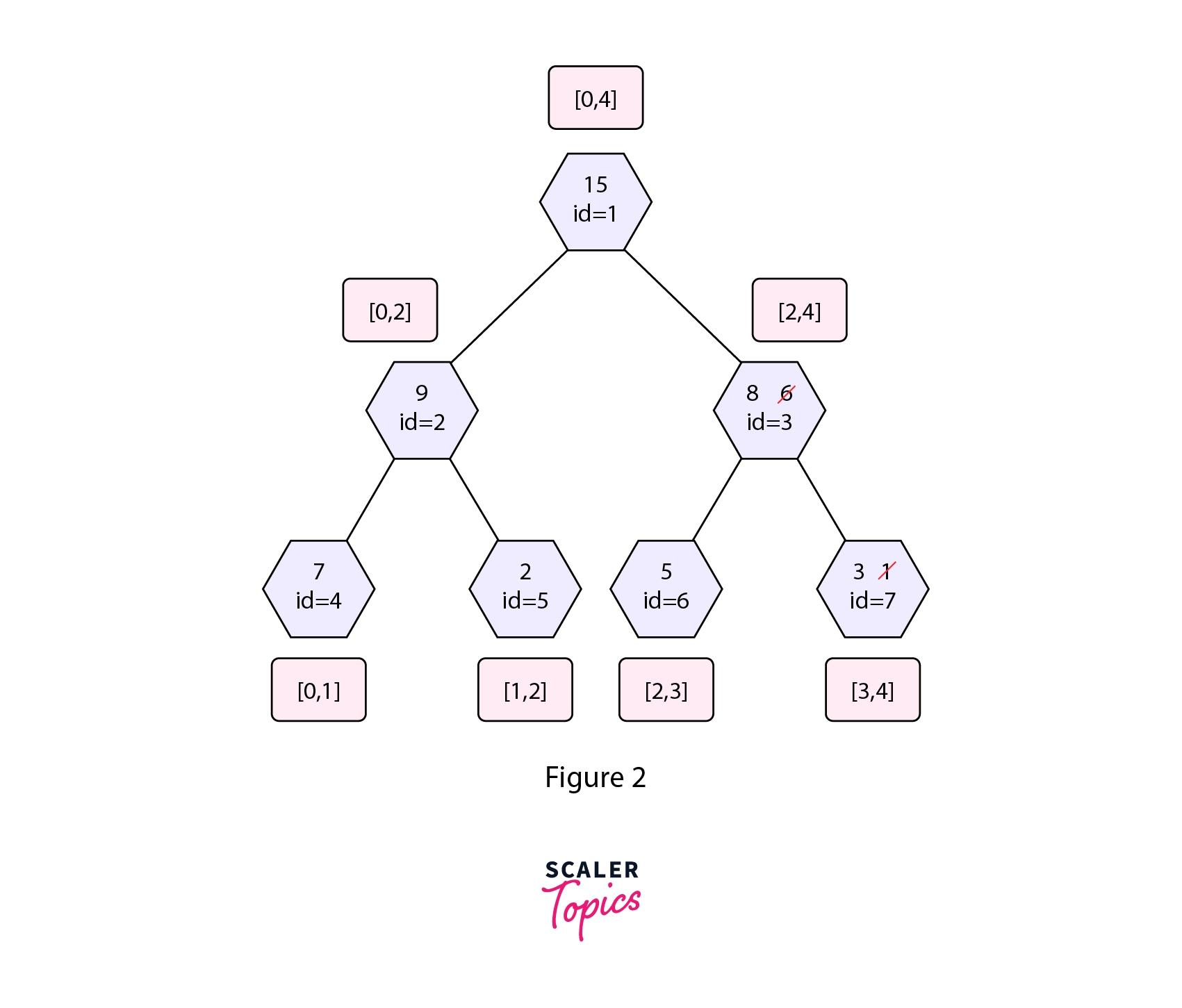
In the segment tree shown in figure 2, we can see that only three nodes get affected while the value in the other nodes remains the same. These three nodes fall in the path from the root to the leaf node that we updated.

In a Persistent Segment Tree, we use the fact that the height of a Segment Tree can’t be more than $O(log n)$. Since in a point update query we move to a leaf node and update all the nodes in its path from the root to that leaf node. There can’t exist more than $O(log n)$ number of nodes that we need to update in an update operation as the height of a Segment Tree can’t exceed $O(log n)$. Thus we only make an $O(log n)$ number of nodes and store it in the new version of the Segment Tree. While rest of the nodes in the new version are shared from the previous version as they remain unchanged in the update operation.

The basic idea behind a Persistent Segment Tree is that in the new version of our segment tree, we only create $O(log n)$ number of nodes that are updated and the rest of the nodes are shared from the previous version.

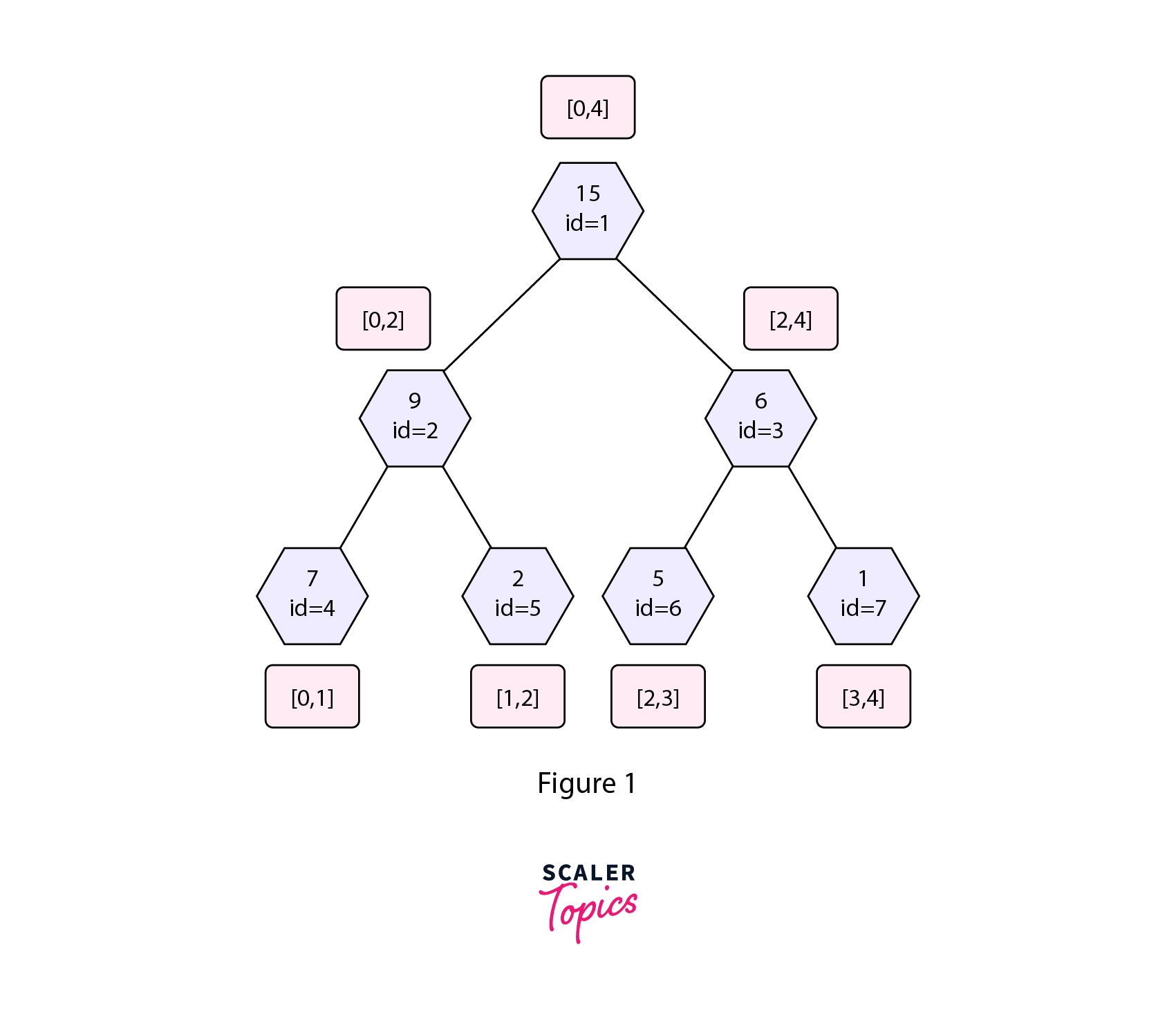
The diagram above shows the structure of a Persistent Segment Tree used for range sum queries.

As in the update operation discussed above only three nodes were changing, i.e the nodes with value= 15, 6, 1. Thus we only make three new nodes in the new version of the segment tree. These new nodes are shown by red color in the Persistent Segment Tree shown above. The new nodes in Version-1 shares nodes with Version-0 of the Segment Tree. This way we are able to do the update operation in $O(log n)$ space complexity as we only make an $O(log n)$ new nodes in an update query.

After the update query, we have preserved the past state, i.e Version-0. We build Version-1 of the segment tree by creating only those nodes that were modified while sharing the other nodes from the previous version. In a similar way, we can build the Version-2 with help of the Version-1 of the Segment Tree and so on.

Thus a Persistent Segment Tree can consist of multiple versions depending on the number of update operations. Let us understand how we can solve the problem discussed below using a Persistent Segment Tree.

Problem Statement

You are given an array arr[ ] and you have to handle point updates in the given array and solve range sum queries or find the sum in a given range after the Kth update operation. You have to achieve this using $O(log n)$ extra space for each update operation and $O(log n)$ time complexity for each query operation.

How We Can Efficiently Solve The Problem Using a Persistent Segment Tree

We can use a Persistent Segment Tree to solve the above problem in an efficient way. We build the Segment tree using the data present in the array arr[ ]. Lets name this version of the segment tree as Version-0. Now as the update operations are performed we upgrade the most recently updated version of the segment tree to a new version using the idea discussed above. This way we can perform an update operation in $O(log n)$ time and space complexity. Finally we can solve range sum queries in the required version of the Segment Tree using the same technique we use for a simple segment tree. Lets us discuss in detail how we can implement the build query, the upgrade query and the range sum query in a Persistent Segment Tree.

Build Function for a Persistent Segment Tree

The BuildPersistentSegmentTree function takes a pointer to the root node, left range and the right range associated with the node, and the parent vector (a vector or an array that stores the data from which the Version-0 of Segment tree is built) as parameters. Note that while assigning ranges to the nodes we will use LeftRange as inclusive and RightRange as exclusive. Using the BuildPersisitentSegmentTree function we build Version-0 of our persistent segment tree (0 based indexing).

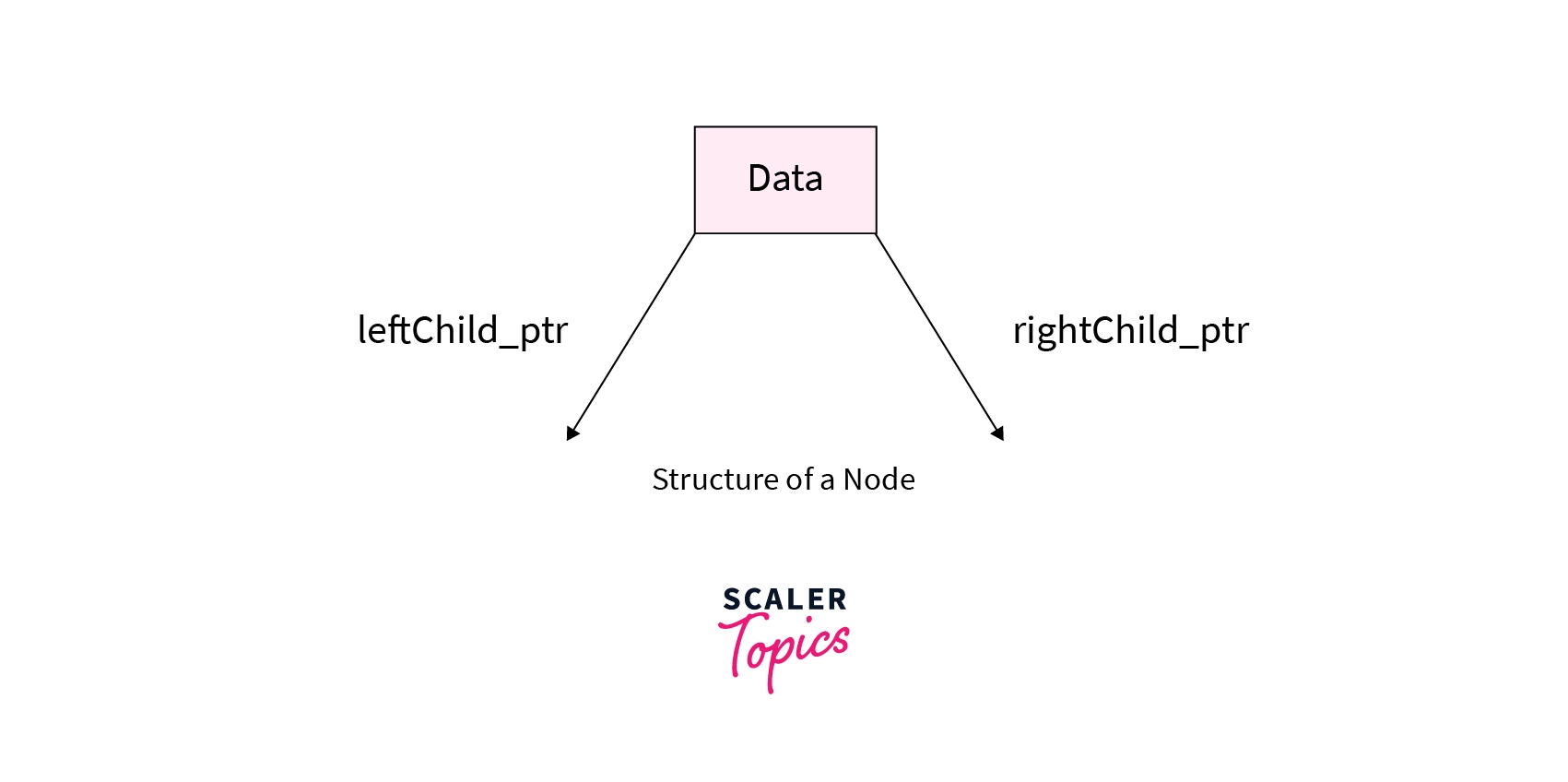
We build a structure of a node with three fields.

• The first field stores the data present in the node. Let’s name this variable data.
• The second field is a pointer that points to the left child of the current node. Let’s name this pointer leftChild_ptr.
• The third field is also a pointer that points to the right child of the current node. Let’s name this pointer rightChild_ptr.

The diagram below shows the structure of a node in a Persistent Segment Tree.

Let’s define a function BuildPersistentSegmentTree(current_node, parentVector, leftRange, rightRange) that will build the segment tree from the data present in the parentVector. Note that we can also use an array instead of a vector. The leftRange and rightRange variables will store the left and the right ranges associated with the current_node (LeftRange as inclusive and RightRange as exclusive). We make a new root node for Version-0 of the Segment Tree and initialize the leftChildptr and rightChildPtr of the root node with NULL. We initially pass the root node of Version-0 to the current_node variable in the BuildPersistentSegmentTree function.

We start the dfs call from the root node of the Segment Tree. The range associated with the root node will be [0,n) (LeftRange as inclusive and RightRange as exclusive). Where n is the number of elements in the parentVector. We reach a leaf node whenever we get a condition of RightRange-LeftRange equal to 1 for any node. We build the Segment Tree recursively using the bottom-up recursion technique.

In the case of a non-leaf node, we assign new nodes to the leftChildPtr and rightChildPtr of the current_node. Then we recursively build the segment tree for both the right and left halves of the current_node. While backtracking we store the sum of the values present in the left and the right child in the current_node.

In the case of a leaf node, i.e when RightRange-LeftRange for any node will be equal to 1. We assign the value present at the LeftRange index of parentVector in the current_node. As because this is the node in the segment tree that represents that element in the parentVector. Then we return from the dfs call. The diagram below shows the structure of a Segment Tree used for finding sum in a given range after the build query where each node stores the sum associated with a particular range of the parent vector.

Pseudocode For The Build Operation

Refer to the pseudocode below for the build function of a range sum persistent segment tree-

//Make the structure for a node
struct Node {
    int data;
    //points to left child of current node
    Node *leftChildPtr;
    //points to right child of current node
    Node *rightChildPtr;
    //default constructor
    Node() {}
    //constructor to assign values to a node
    Node(int _data, Node *_left, Node *_right)
    {
        data = _data;
        leftChildPtr = _left;
        rightChildPtr = _right;
    }
};
// start the dfs traversal from the root node
void BuildPersistentSegmentTree(Node *currentNode,int LeftRange,int RightRange,vector<int>&parentVector)
{
    //if leafnode
    if(RightRange-LeftRange==1)
    {
        currrentNode->data=parentVector[leftRange];
        // Assign the value indicated by leftRange in the ParentVector
        return;
    }

    Assign the Left and Right child of the currentNode.

    Recursively Build the Left half.
    Recursively Build the Right half.

    Store the sum of the left and right child in the currentNode.
}

Upgrade Function for a Persistent Segment Tree

Let’s say we want to update a particular node in Version-k of the Segment Tree (where k is any non-negative integer). But since we are using a Persistent Segment Tree we will not update that node directly. We will make a new version of the segment tree, say Version-(k+1) that will share nodes from the previous version, i.e Version-k of the Segment Tree. Since we are making a new version we also make a new root node for the Version-(k+1) of the Segment Tree. We initialize the leftChildPtr and rightChildPtr of the root node of Version-(k+1) with NULL.

Let’s define a function
UpgradePersistentSegmentTree(root_Version-k,root_Version-k+1,updatePos,updateValue) that will upgrade the Version-k of the segment tree to Version-(k+1) by making a point upgrade operation in Version-k of the Segment Tree. By point upgrade operation we mean that we will first upgrade the Version-k of the segment tree to Version-k+1 and then make the point update operation in Version-k+1 of the segment tree in a single operation. Initially, we pass the root nodes of version k and k+1 to the UpgradePersistentSegmentTree function.The updatePos variable will store the index of the parent vector that needs to be updated. Parent vector here refers to the vector from which Version-0 of the segment tree was built. The updateValue will store the updated value for the point upgrade operation.

Refer to the segment tree shown in figure 1. Let’s suppose we want to update the leaf node with value=1 to value=3. As we are building a new version, say Version-1 we will also need a new root node. The nodes that will be affected by this update operation are nodes with values=15, 6, 1. Let’s understand the approach we will use for building the Version-1 of the Segment Tree.

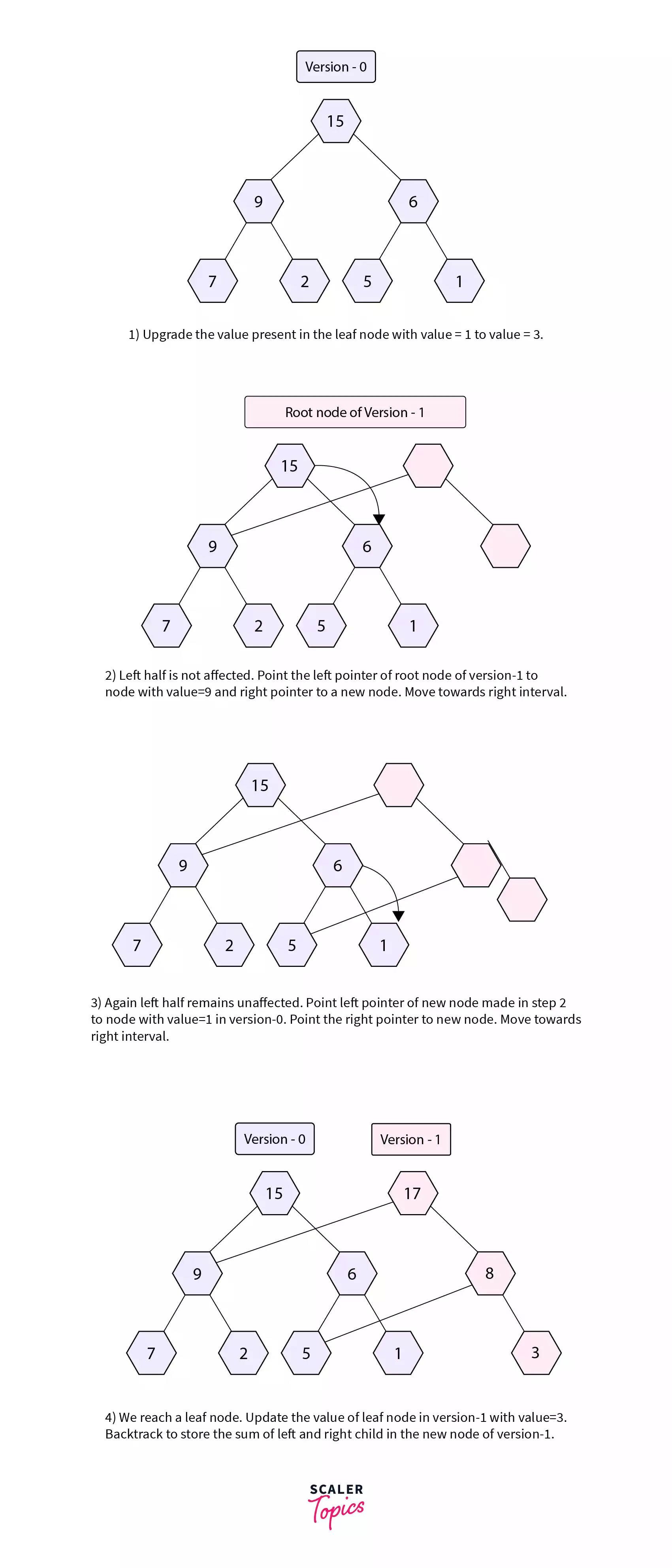
We start the dfs traversal from the root node of the segment tree of Version-0. This is shown by step 1 in the diagram shown above.

In step 2, we check whether the right or the left half associated with the root node remains unaffected by the given update operation. In the given update operation the left half will remain unaffected. This is because the node to be updated falls in the right interval of the current node which is the root node. Thus we point the leftChildPtr of the root node of Version-1 to the node with value=9 in Version-0 as this half will not be affected with the given update operation.

We make a new node and point the rightChildPtr of the root node of Version-1 to the new node. We then recursively move towards the right half of the root node of Version-0 as the left half is unaffected.

In step 3, we again check which half will remain unaffected by the given update operation. As the node to be updated falls in the right interval of the node with value=6 in Version-0 the left half will again remain unaffected by the given update operation. Thus we point the leftChildPtr of the node with value=8 in Version-1 to the node with value=5 in Version-0. The rightChildPtr will be pointed to a new node. We again recursively move towards the right of the node with value=6 in Version-0 and reach a leaf node.

When we reach a leaf node we get the node we want to update. We assign the updated value in the leaf node of Version-1 and return from the dfs call. While backtracking we update the value of the non-leaf nodes in Version-1 with the sum of the right and left child of the current node in Version-1. This is shown by step 4 of the diagram shown above.

After the upgrade operation, the segment tree will look like the one shown in figure 3. The red nodes represent the new nodes that were created in the upgrade operation. The rest of the nodes were shared from the previous version that is Version-0 of the segment tree.

How do we keep track of all the versions of the Segment Tree ?

To keep track of all the previous versions of the segment tree we can store the root nodes of all the previous versions in an array or a vector. With the help of the root node, we can access all the nodes that are associated with that root node of the Segment Tree.

We create a new root node every time we apply an upgrade operation in our Segment Tree. Thus before applying the upgrade operation we make a new root node then store it in a vector or an array. We will use a vector to store root nodes of all the previous versions of the segment tree. Let’s name this vector as version, version[0] will store the root node of the 0th version of the Persistent Segment tree and so on.

We pass the new root node and the root node of the previous version to the UpgradePersistentSegmentTree function. Let us look at the pseudocode for UpgradePersistentSegmentTree function.

Pseudocode For The Upgrade Operation

The UpgradePersistentSegmentTree function takes 6 parameters –

• A pointer that will point to the nodes of the current version that is to be built.
• A pointer that points to the nodes of the previous version of the segment tree, i.e one version less than the current version. We initially pass the root node of the previous version to this pointer.
• The left and right range associated with nodes of the segment tree ( Left range inclusive and Right range exclusive).
• The update position (0 based indexing), i.e the position of the parent array that needs to be updated. Parent array refers to the array from which the Version-0 of the segment tree was built.
• The update value for the update operation.

Let us now look at the pseudocode for upgrade operation in a Persistent Segment tree. Note that we will look at the entire implementation of the algorithm later in this article.

//Make a dfs call from the root node of the previous version.
void UpgradePersistentSegmentTree(Node *prevNode, Node *currentNode, int LeftRange, int RightRange, int updatePosition, int updateData)
{
//if leaf node
if(RightRange-LeftRange==1)
{
//we get the leaf node we want to update
update the leaf node of the current version with updateValue
return;
}

int mid=(LeftRange+RightRange)/2;

//check the half which will get affected
if(updatePosition < mid)
{
    //Right half nodes will remain unaffected
    Point the rightChildPtr of currentNode to the rightChildPtr of the prevNode.
    Make a new node and point the leftChildPtr of the currentNode to the new node.

    Recursively call the UpgradePersistentSegmentTree for the left interval only.
}
else
{
    //Left half nodes will remain unaffected
    Point the leftChildPtr of currentNode to the leftChildPtr of the prevNode.
    Make a new node and point the rightChildPtr of the currentNode to the new node.

    Recursively call the UpgradePersistentSegmentTree for the right interval only.
}
Set the data for the non-leaf nodes with the sum of the value present in its left and right child.

}

Query Function For a Persistent Segment Tree

The conditions of `No Overlap`, `Partial Overlap`, and `Complete Overlap` will be the same as those discussed for a Simple Segment Tree used for range queries. Let us briefly discuss each of them.

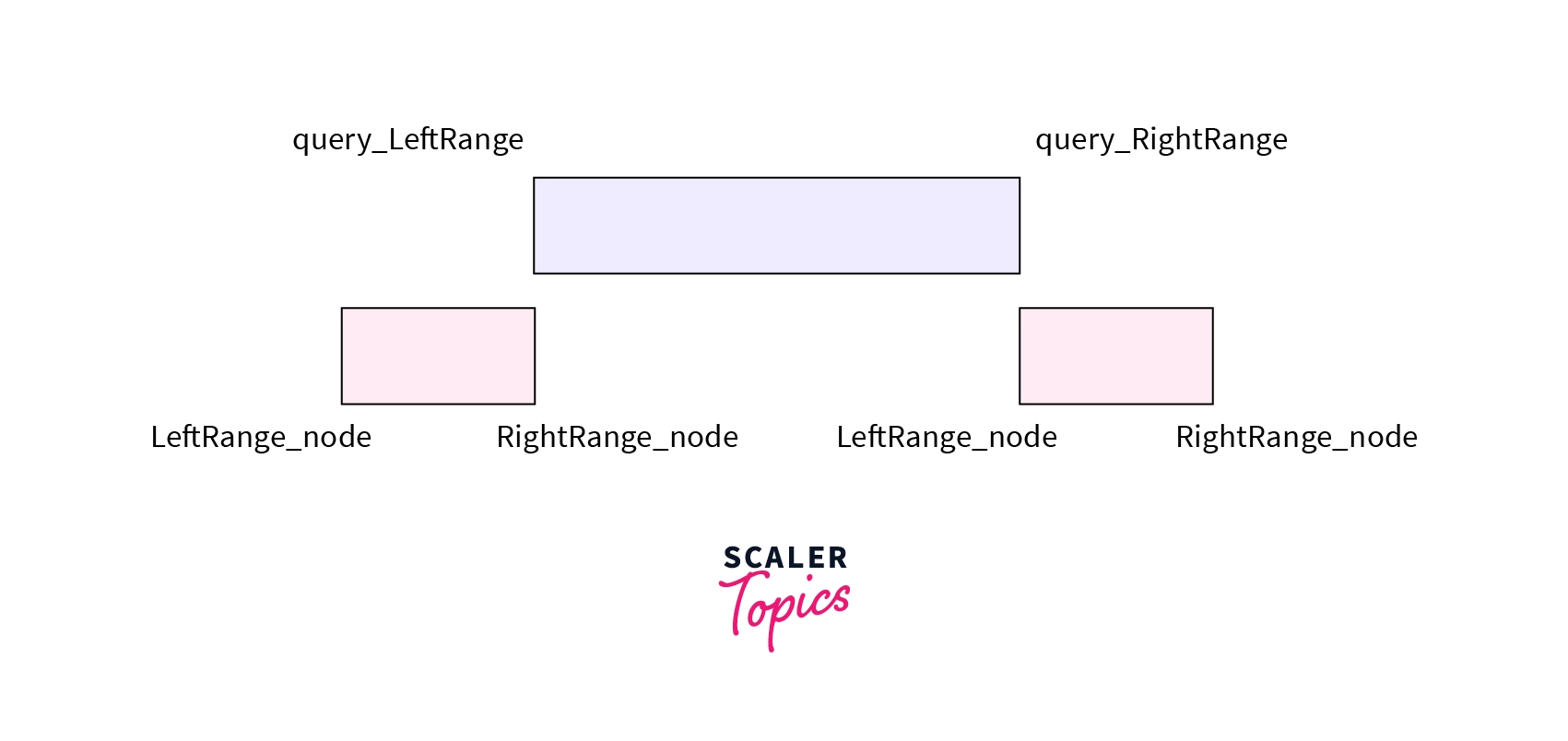
* **No Overlap** – The range associated with node falls completely outside the range asked in the query. i.e `RightRange_node <= query_LeftRange or LeftRange_node >= query_RightRange`. Note that we are taking `equal to` as we are taking the ranges as `right range exclusive and left range inclusive` manner.


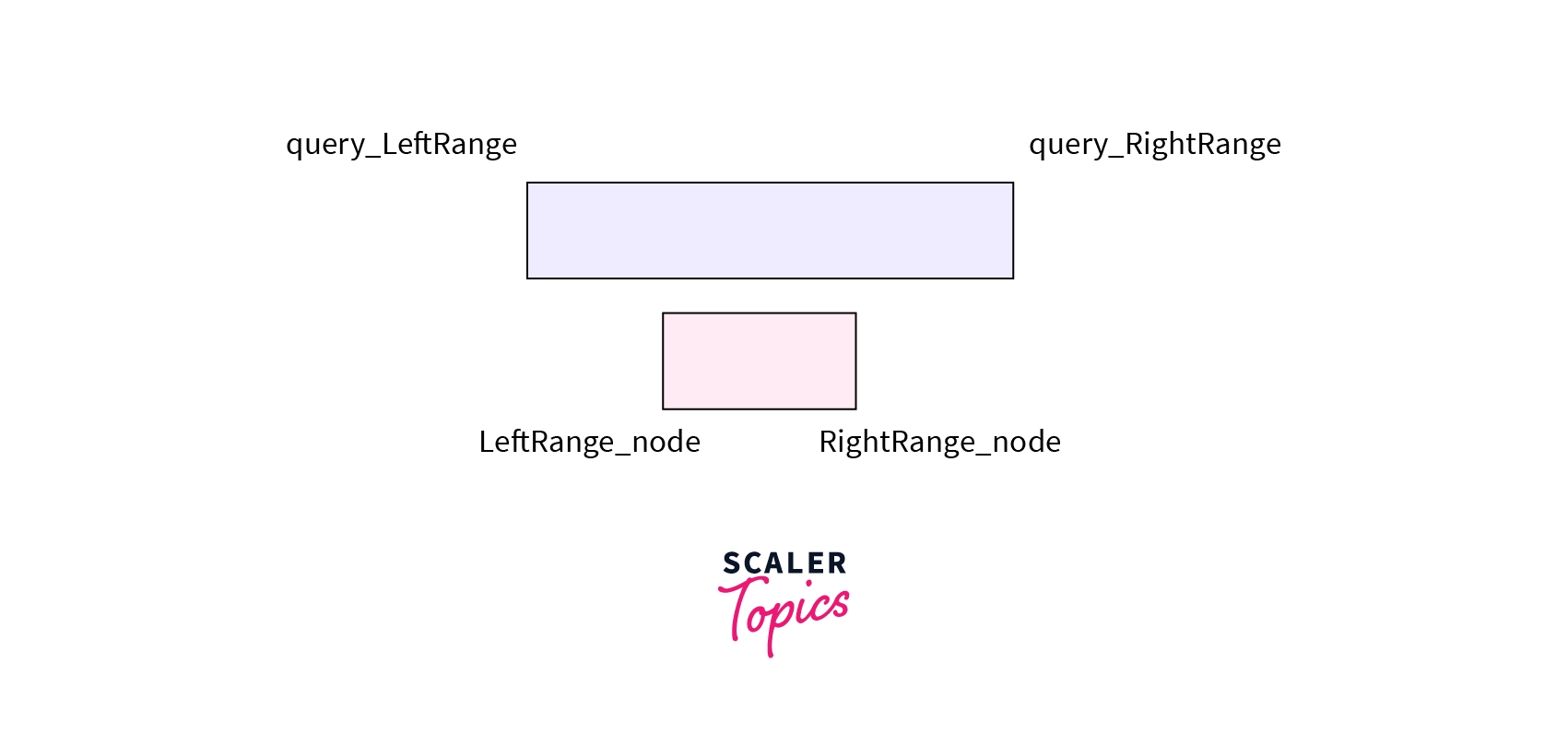
* **Complete Overlap** – The range associated with node falls completely inside the range asked in the query. i.e `LeftRange_node >= query_LeftRange and RightRange_node <= query_RightRange`.


* **Partial Overlap** – The range associated with the node falls partially inside and partially outside the range asked in the query. If both the above condition fails it will be a case of partial overlap.



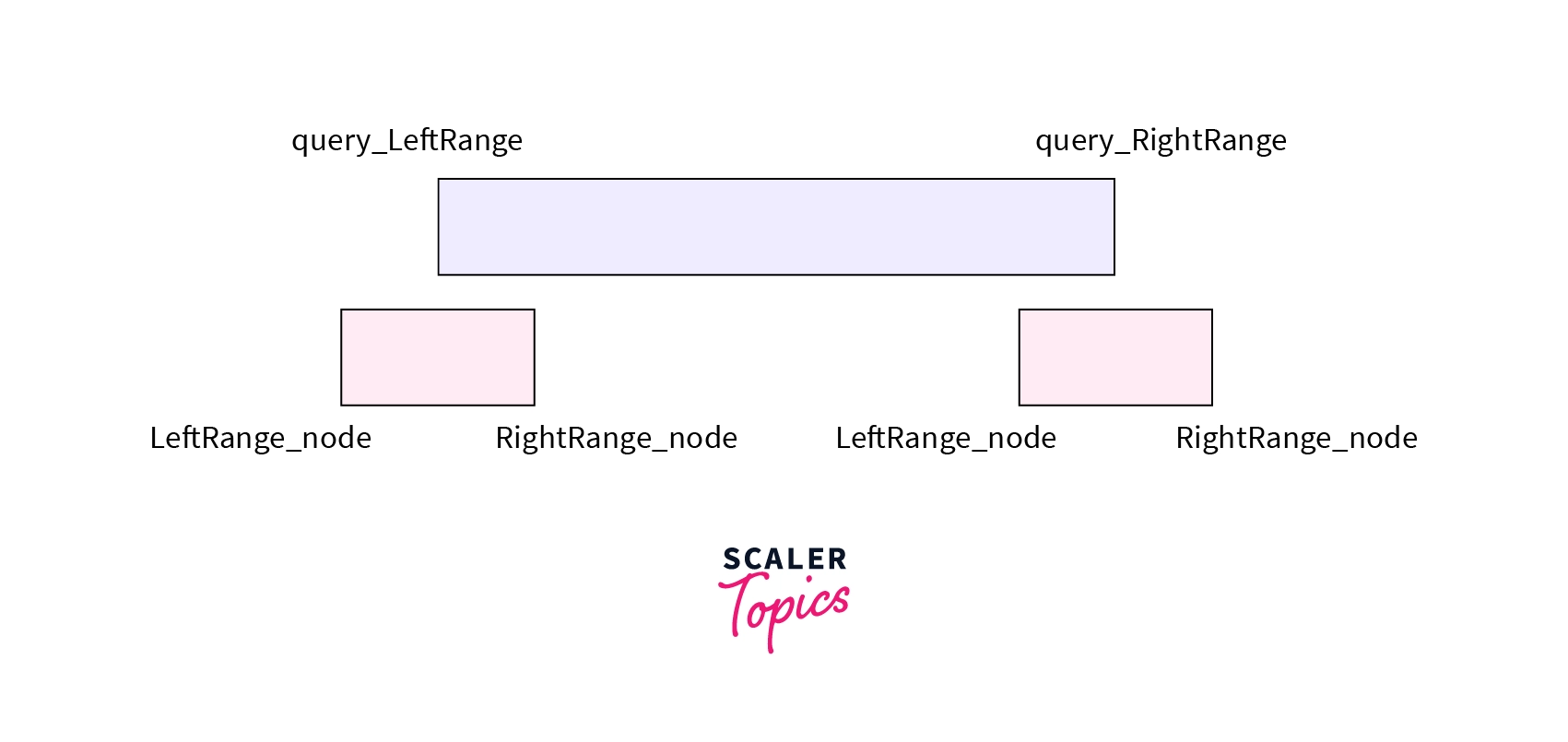
The query function takes the root node of the required version, the left and the right range associated with the current node and the range asked in the query, i.e `query_LeftRange & query_RightRange` as parameters.

We run a dfs traversal from the root node of the required version of the segment tree. In the dfs traversal, we check for the condition of complete overlap, no overlap, and partial overlap. When we get a condition of `complete overlap` we `return the value present in that node` of the segment tree as our answer. In the case of `no overlap`, we `return 0` as this will never affect our answer in the case of addition. In case of `partial overlap`, we recursively look for the answer in both the right and the left half. Then we `return the combined` answer from both the `left and right halves`. Let us look at the pseudocode for the query function in a Persistent Segment tree.

Pseudocode for Query Function in a Persistent Segment Tree

Let’s define a function `RangeSumPersistentSegementTree(Version-k, query_LeftRange, query_RightRange)` as the sum in the range from `query_LeftRange to query_RightRange-1`, i.e `[query_LeftRange , query_RightRange-1]` in the `Version-k` of the Segment Tree. We pass the root node of the required version of the segment tree to the query function. Refer to the pseudocode for the `RangeSumPersistentSegementTree` function shown below.

//Make a dfs call from the root node of the required version of the segment tree
//Initially pass the root of the required version to the currentNode pointer.
int RangeSumPersistentSegementTree(Node *currentNode, int LeftRange, int RightRange, int query_LeftRange, int query_RightRange)
{
if(condition of complete overlap)
{
return the value present in the currentNode of the Segment Tree.
}
else if(condition of no overlap)
{
// return 0 as it will not affect the answer in case of addition operation.
return 0;
}
//if both the above condition fails we will get the condition of Partial Overlap.

Recursively get the answer from its left child.
Recursively get the answer from its right child.

return the combined answer or 
the sum of the value obtained from left and right child.

}

Implementation Of a Persistent Segment Tree

Let us now look at the implementation of a Persistent Segment Tree.
* At first, we build `Version-0` of our persistent segment tree using the `BuildPersistentSegmentTree` function with the data present in the vector, `parentVector`.
* Then we build `Version-1` and `Version-2` of the segment tree using the `UpgradePersistentSegmentTree` function with the help of its previous versions.
* We will use the `version` vector to store the root node of all the versions of the segment tree.
* Finally, we solve range sum queries in all three versions using the `RangeSumPersistentSegementTree` function.

C++ Implementation –

#include<bits/stdc++.h>
using namespace std;

struct Node {
	int data;
	Node *leftChildPtr;
	Node *rightChildPtr;

	Node() {}
	Node(int _data, Node *_left, Node *_right)
	{
		data = _data;
		leftChildPtr = _left;
		rightChildPtr = _right;
	}
};


void BuildPersistentSegmentTree(vector<int>&parentVector, Node *currentNode, int LeftRange, int RightRange)
{
    //if leaf node store the data in the current node
	if (RightRange - LeftRange == 1)
	{
		currentNode->data = parentVector[LeftRange];
		return;
	}

	int mid = (LeftRange + RightRange) / 2;
	currentNode->leftChildPtr = new Node(0, NULL, NULL);
	currentNode->rightChildPtr = new Node(0, NULL, NULL);
    
    //recursively build the left half
	BuildPersistentSegmentTree(parentVector, currentNode->leftChildPtr, LeftRange, mid);
    //recursively build the right half
	BuildPersistentSegmentTree(parentVector, currentNode->rightChildPtr, mid, RightRange);
    
    //store the sum of left and right child in the current node
	currentNode->data = currentNode->leftChildPtr->data + currentNode->rightChildPtr->data;
}

void UpgradePersistentSegmentTree(Node *pastNode, Node *currentNode, int LeftRange, int RightRange, int updatePosition, int updateData)
{

	if (RightRange - LeftRange == 1)
	{
		currentNode->data = updateData;
		return;
	}
	int mid = (LeftRange + RightRange) / 2;
    //check which half will remain unaffected with the update operation
	if (updatePosition < mid)
	{
        //right half will not be affected
		currentNode->rightChildPtr = pastNode->rightChildPtr;

		currentNode->leftChildPtr = new Node(0, NULL, NULL);
        
        //recursively solve for the left half only
		UpgradePersistentSegmentTree(pastNode->leftChildPtr, currentNode->leftChildPtr, LeftRange, mid, updatePosition, updateData);
	}
	else
	{
        //left half will not be affected
		currentNode->leftChildPtr = pastNode->leftChildPtr;

		currentNode->rightChildPtr = new Node(0, NULL, NULL);
        
        //recursively solve for the right half only
		UpgradePersistentSegmentTree(pastNode->rightChildPtr, currentNode->rightChildPtr, mid, RightRange, updatePosition, updateData);
	}
	currentNode->data = currentNode->leftChildPtr->data + currentNode->rightChildPtr->data;
}

int RangeSumPersistentSegementTree(Node *currentNode, int LeftRange, int RightRange, int query_LeftRange, int query_RightRange)
{

	if (LeftRange >= query_RightRange || RightRange <= query_LeftRange || LeftRange >= RightRange || !currentNode)
	{
        //condition of no overlap
		return 0;
	}
	if (LeftRange >= query_LeftRange && RightRange <= query_RightRange)
	{
        //condition of total overlap

		return currentNode->data;
	}
    // condition of partial overlap
	int mid = (LeftRange + RightRange) / 2;
    // recursively solve for the left half
	int leftSegmentSum = RangeSumPersistentSegementTree(currentNode->leftChildPtr, LeftRange, mid, query_LeftRange, query_RightRange);
    //recursively solve for the right half
	int rightSegmentSum = RangeSumPersistentSegementTree(currentNode->rightChildPtr, mid, RightRange, query_LeftRange, query_RightRange);
    
    //return the sum obtained from the left and right halves
	return leftSegmentSum + rightSegmentSum;
}

int main()
{
	int num_nodes;

	num_nodes = 4;

	vector<int>parentVector(num_nodes);

	parentVector = {7, 2, 5, 1};
    
    //Build the Version-0 of the Segment Tree
	Node *root = new Node(0, NULL, NULL);

	BuildPersistentSegmentTree(parentVector, root, 0, num_nodes);

	vector<Node *>version(100);
    
    //store the root node of version-0 in the version vector.
	version[0] = root;

    // make root nodes for Version-1 and Version-2 and store them in the version vector
	version[1] = new Node(0, NULL, NULL);
	version[2] = new Node(0, NULL, NULL);
    
    //upgrade the version-0 of the Segment tree to version-1 
    //by passing the root node of version-0 in prevNode poniter 
    //and root node of version-1 in currentNode pointer. 
	UpgradePersistentSegmentTree(version[0], version[1], 0, num_nodes, 3, 3);
    
    //upgrade the version-1 of the Segment tree to version-2 
    //by passing the root node of version-1 in prevNode poniter 
    //and root node of version-2 in currentNode pointer. 
	UpgradePersistentSegmentTree(version[1], version[2], 0, num_nodes, 1, 10);

    //solve range sum queries
	cout << "RangeSumPersistentSegementTree(0,5) on Version 1 = ";
	cout << RangeSumPersistentSegementTree(version[1], 0, num_nodes, 0, 4) << "\n";
	cout << "RangeSumPersistentSegementTree(3,5) on Version 2 = ";
	cout << RangeSumPersistentSegementTree(version[2], 0, num_nodes, 3, 4) << "\n";
	cout << "RangeSumPersistentSegementTree(0,4) on Version 0 = ";
	cout << RangeSumPersistentSegementTree(version[0], 0, num_nodes, 0, 4) << "\n";
}

Time Complexity

Build Query

A Segment tree can contain a maximum of $4*n+1$ nodes (1 based indexing). As we visit every node once in the dfs traversal while building the Segment Tree. Hence the time complexity of the build function is $O(n)$. Note that here we consider that the making of new nodes is done in $O(1)$ time complexity.

Upgrade Query

In an upgrade query, we move to the leaf node that needs to be updated. While backtracking we update the value in the non-leaf nodes of the newer version of the segment tree with the sum of the value present in its left and right child. As the height of a Segment Tree can’t be more than $ceil(log n)$ (where n is the number of elements in the parent array). Thus we only move to a depth of $O(log n)$ to reach the leaf node in our dfs traversal. Hence the time complexity for the upgrade query is $O(log n)$. Here also we consider that the making of new nodes is done in $O(1)$ time complexity.

Range Sum Query

The time complexity for a range sum query in a Persistent Segment Tree is the same as that in a Simple Segment Tree. As the addition of two numbers is done in $O(1)$ time complexity thus a Range Sum Query in a Persistent Segment Tree takes a time complexity of $O(log n)$.

Applications of a Persistent Segment Tree.

• We use a Persistent Segment Tree when we want to store the previous results as well as handle point updates and answer range queries on the segment tree after the Kth update efficiently.
• A Persistent Segment Tree can also be used to find the Kth minimum or maximum over a given range efficiently.

Conclusion

• Persistent Data Structures are mainly used in Version Controls like Git and others. It enables multiple users to work in a particular version and to make updates without affecting the old version.
• A Persistent Segment Tree enables us to make new versions from the older versions efficiently. The new version of the Persistent Segment Tree shares nodes from the previous version. New nodes are created for only those nodes that were changed by the update operation in the previous version of the Segment Tree.