The Nim Game is a combinatorial game that involves a number of piles of stones/coins and two players playing the game. In each turn, one player chooses a pile and removes a non-zero number of stones/coins from the pile. The person who cannot make a move loses in the end. We explore the Nim Game in this article and also define its solution.
Scope of the Article
- This article provides a detailed intuition and solution behind the
Nim Game. Apart from the solution this article also looks at various examples and the working of the solution for a better understanding of the Nim Game. - This article discusses the solution to Nim Game in C++.
Takeaways
Time Complexity and Space complexity of the Nim game solution is $O(n)$
What is Game of Nim?
The Game of Nim or Nim game is a mathematical combinatorial game in which we have a pile of some objects, say coins in this case, and two players who will take turns one after the other. In each turn, a player must pick at least one object(coin in this case), and may remove any number of objects(coins) given that they all belong to the same pile. The game is won by the one who picks the last object(coin).
The game of Nim was initially developed to be played as a misère game, which means the player to take the last object losses the game. Nowadays the game has been modified to be played as a typical normal game which means the player taking the last object wins. In this article, we shall consider the game of nim to be a normal game and discuss the version in which the player picking the last object wins.
Problem Statement
Let us formally state the problem before moving on to the approach and solution.
Given some number of piles that contain one or more coins/stones. In each turn, a player will select a pile and remove at least one or more coins/stones from the chosen pile. The player who cannot make a move in the end loses.
Let us look at an example before we explore how it can be solved.
Example
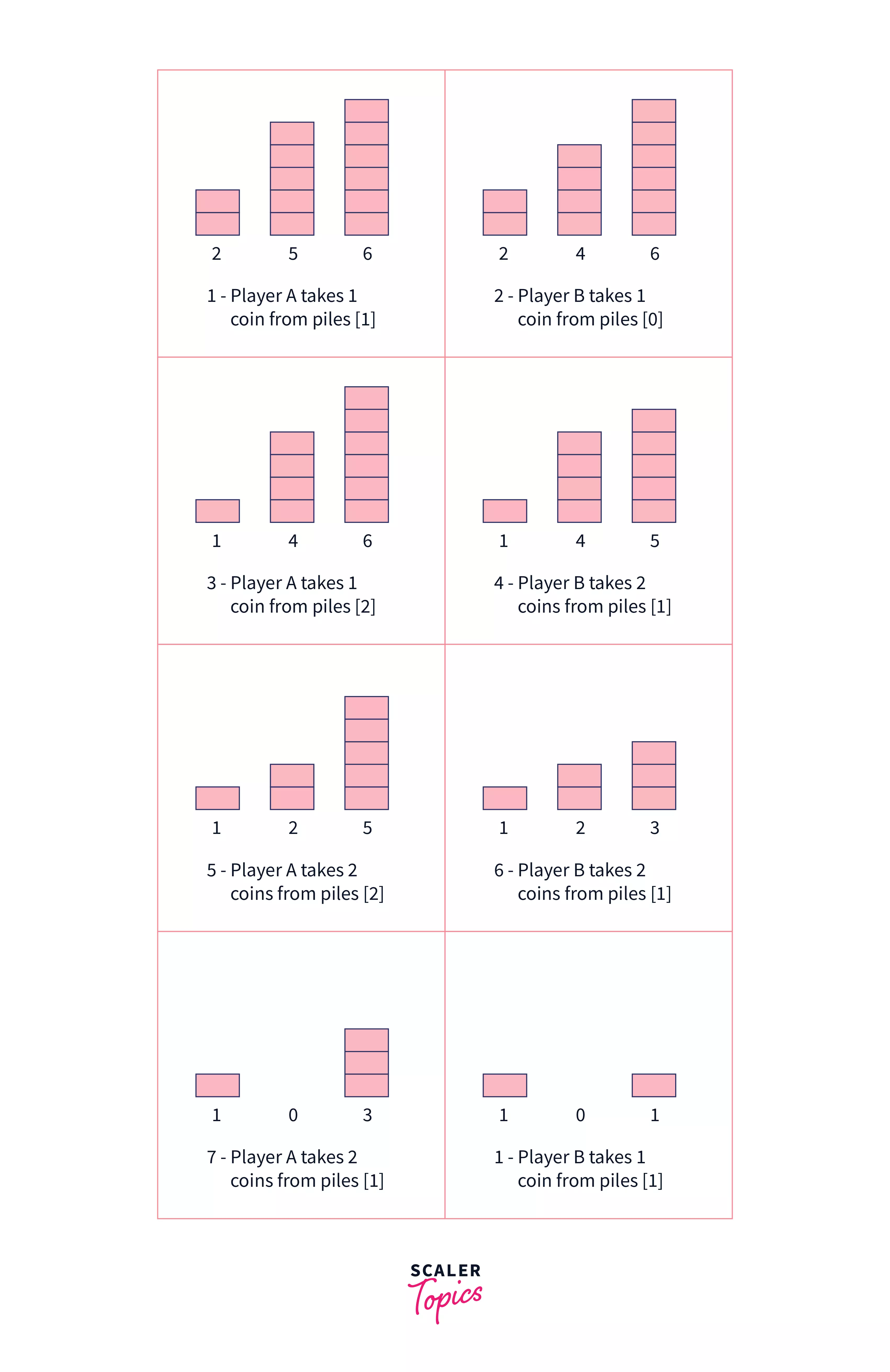
Given piles of coins are:
$Piles[] = { 2, 5, 6}$
Let us look at the step by step process in which the game will proceed if Player A starts first.
| Piles[0] | Piles[1] | Piles[2] | Move |
|---|---|---|---|
| 2 | 5 | 6 | Initial configuration of the game |
| 2 | 4 | 6 | Player A picks 1 coin from piles[1] |
| 1 | 4 | 6 | Player B picks 1 coin from piles[0] |
| 1 | 4 | 5 | Player A picks 1 coin from piles[2] |
| 1 | 2 | 5 | Player B picks 2 coins from piles[1] |
| 1 | 2 | 3 | Player A picks 2 coins from piles[2] |
| 1 | 0 | 3 | Player B picks 2 coins from piles[1] |
| 1 | 0 | 1 | Player A picks 2 coins from piles[2] |
| 1 | 0 | 0 | Player B picks 1 coin from piles[2] |
| 0 | 0 | 0 | Player A picks 1 coin from piles[0] and wins the game |
As shown in the example, Player A takes the last coin and is the winner.
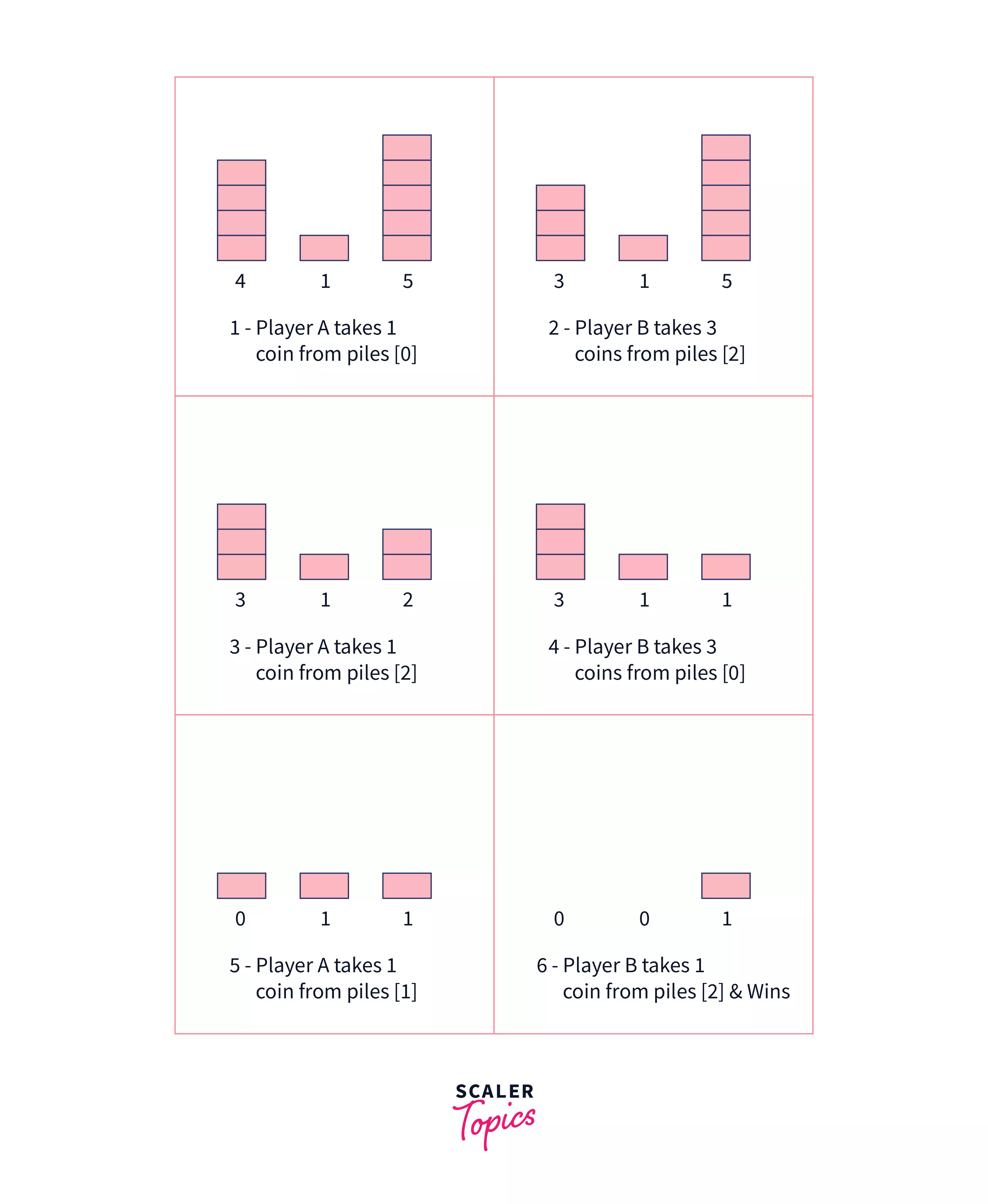
Let us take a look at another example
$Piles[] = { 4, 1, 5}$
| Piles[0] | Piles[1] | Piles[2] | Move |
|---|---|---|---|
| 4 | 1 | 5 | Initial configuration of the game |
| 3 | 1 | 5 | Player A picks 1 coin from piles[0] |
| 3 | 1 | 2 | Player B picks 3 coins from piles[2] |
| 3 | 1 | 1 | Player A picks 1 coin from piles[2] |
| 0 | 1 | 1 | Player B picks 3 coins from piles[0] |
| 0 | 0 | 1 | Player A picks 1 coin from piles[1] |
| 0 | 0 | 0 | Player B picks 1 coin from piles[2] and wins the game |
This time Player B wins the game as he takes the last coin.
Approaching Solution
We need to understand the fact that both the players will play the game optimally and would not make a mistake that will hamper their chances of winning while finding a solution. Let us now introduce some terms and representations that we’ll be using ahead for the solution.
To represent the number of coins in the ith pile, we’ll say piles[i] ( 0 <= i < n) which also means that there is an array named piles of length n. We shall call the first player as Player A and the second player as Player B.
From the example that we saw above, we can say that the winner of the game surely depends on the configuration of the piles and the player who starts first.
Let us now introduce a new term called Nim Sum which will play an important role in finding out the final solution and we’ll see how.
Nim-Sum
At any point of time during the duration of the game, we define the Nim sum as the cumulative Exclusive-OR (XOR) value of all the coins in each pile.
We now know what Nim-Sum(cumulative XOR or XOR sum) is, but why do we need it? It is necessary to know about Nim-Sum as it is a part of a lemma that gives the solution to the Nim Game. We’ll now state the lemma and prove it later.
Lemma: If both the player’s A and B are playing the game optimally, which means that they don’t make any moves that may hamper their chances of winning. In that case, if the Nim sum of the initial configuration is non-zero, the player making the first move is guaranteed to win the game and if the Nim sum of the initial configuration is zero the second player will win the game.
Let us look at why this lemma is true, and in turn, find out what is the optimal strategy to be followed.
Optimal Strategy
The Game of Nim or Nim Game can be mathematically solved for any initial configuration of piles of coins and the winner of the game be computed beforehand with the constraint that both the players play optimally and do not make any mistakes that may hamper their chances of winning the game.
To solve the game of Nim we will use the mathematical operation known as the “Exclusive-Or” or XOR.
Let us note down some of the facts about Exclusive-Or (XOR) to understand the optimal strategy:
- If the Nim sum or
XOR sum(cumulative XOR)of N numbers is already Zero, then we can never make theXOR sumzero by reducing asingle number once.
Example: Consider an initial configuration of 3 piles having coins 1,4 and 5 respectively having cumulative XOR(Nim Sum) as 0.

Removing some number of coins from any of the piles can be treated as flipping some finite (single or multiple) amounts of bits in the binary representation of any one of the piles. This operation will always result in a non-zero cumulative XOR(Nim Sum).
- If the Nim sum or XOR sum(cumulative XOR) of N numbers is non-zero, then there is at least one number, which when reduced makes the
XOR sum equal to Zero.
Example: Consider an initial configuration of 3 piles having coins 3,4 and 5 respectively and having non-zero cumulative XOR.
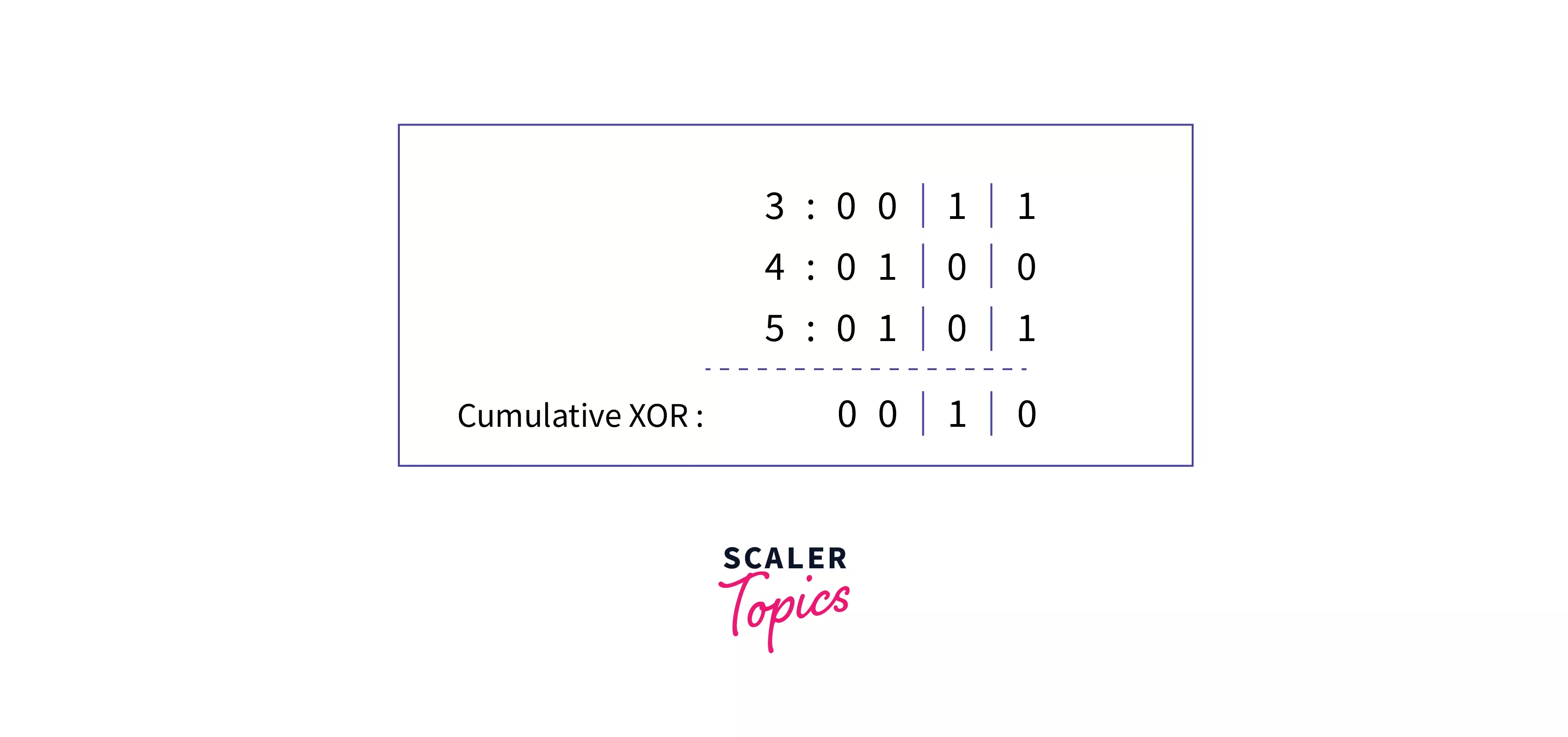
In this case, that is the Cumulative XOR or the Nim sum is non-zero, then you can always remove some ${x}$ number of coins from some pile such that the new cumulative XOR(Nim sum) becomes $0$. In this example you can remove 2 coins from any of the piles of the coin and the resultant Cumulative XOR or the Nim sum will be equal to zero.
Now that we are done with facts, representation, and terms, let us try to prove the lemma.
Two Cases with the Nim Sum:
Case 1: Initial Configuration of the Piles Have the XOR-sum or the Nim Sum Equal to Zero.
If the Nim sum(cumulative XOR) is already zero then as explained above B will win, let us see why this will happen.
A must pick at least one coin from any of the piles and the Nim Sum was initially zero, then whatever the number of items A removes the new Nim Sum(Xor Sum) would become non-zero ( as we explained above that choosing to remove any number of items will make the Nim Sum non-zero if it was originally zero).
Now it will be B’s turn and B would prefer that his move makes the Nim Sum zero as he is playing optimally, B then would play a move to pick some number of items to remove such that the Nim Sum becomes zero again ( as we explained above that this will always be true that we can make a non zero Nim Sum to a zero Nim Sum).
Now the game will run as long as there are coins remaining in any of the piles to be picked, in each of their turns, A would make the Nim Sum non zero and then B would make the Nim Sum zero if played optimally since the Nim Sum has to be non zero before being the zero( in the end to represent no coins remaining) and we know that B picks whenever the Nim sum is non zero, thus B would win the game by picking the last coins and making the Nim Sum zero.
Let us now discuss the other case where Nim sum was initially non-zero.
Case 2: Initial Configuration of the Piles Has the XOR-sum or the Nim Sum Equal to NonZero.
Now if the Nim sum(cumulative XOR) is initially non zero then A would win the game. Let us try to understand why this would happen, Since initially, the Nim sum is non zero then A would try to make the Nim sum equal to zero by picking the required amount of coins( as we explained above that this will always be true, that we can make a non zero Nim Sum equal to a zero Nim Sum in one move).
Now in B’s turn, as the Nim sum is already zero, it would not matter whatever amount of coins from whichever pile B chooses it will make the Nim sum non zero. Now it will be A’s turn and A would pick the number of coins to make the nim sum equal to zero since he is playing the game optimally and will not make a move to hamper his chances of winning.
The game moves forward in this manner until all the coins from every pile have been removed. Now that we know that in this case whenever the nim sum is non zero A makes a move thus before the last set of coins is picked the nim sum must be non zero which means that A will make the last move and win the game.
Now as we just discussed above in the two cases, it should be clear that the optimal strategy for anyone is to try to make the nim sum zero in their turn if it is possible(that is if the nim sum is non-zero) and if the nim sum cannot be made zero then it wouldn’t matter what move the player makes as it can be easily countered by the other player by making the nim sum zero in his turn(which would be next).
Let us try to implement a solution from the facts that we proved and discussed above.
Implementation
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
void game(vector<int>& piles)
{
// For storing the Nim sum of the initial configuration of all piles
int Nimsum = 0;
for (int i = 0; i < piles.size(); i++)
{
Nimsum ^= piles[i];
}
// If the Nim sum is non-zero then A will win the game
if (Nimsum != 0)
{
cout << "The winner is player A" << endl;
}
// If the Nim sum is zero then B will win the game
else
{
cout << "The winner is player B" << endl;
}
return;
}
int main()
{
// An intial configuration of piles with nim sum equal to zero
vector<int> piles_1 = {1, 2, 3};
game(piles_1);
// An intial configuration of piles with nim sum equal to non zero
vector<int> piles_2 = {3, 4, 5};
game(piles_2);
return 0;
}
Output:
The winner is player B
The winner is player A
As we can see in this solution, the function game() is a void function that prints the winner of the game given the array of piles considering that player A starts first. As explained above, we just need to calculate the Nim-Sum(cumulative XOR) as the XOR of all the integers in the array piles[]. If the resulting value of Nim-Sum is non zero, player A wins else player B wins as discussed in the previous section.
Time and Space Complexity
The Time Complexity of the above-defined solution is $O(n)$ where n is the size of the piles’ array. Similarly, the space complexity is also $O(n)$, where n is the size of the array, for storing the elements in the array piles[]. The additional space complexity, that is the extra space required other than storing the input is $O(1)$ as we just need one variable to store the Nim sum(cumulative XOR).
Conclusion
- The Nim game is a
mathematical combinatorial gamein which we have a pile of some objects and two players who will take turns one after the other to pick some number of objects from one pile. The person who cannot make a move loses. - The Nim sum is defined as the
cumulative Exclusive-OR (XOR)value of all the coins in each pile. - If both players play
optimallyif the Nim sum of the initial configuration is zero, the player making the first move will win else the second player will win. - The
timeandspacecomplexity of the solution is ${O(n)}$ where $n$ is the number of object piles given in the question.
