An N-ary tree or Generic Tree is a tree that can have at most N children. If we replace N with 2 then we get a binary tree. In other words, an n-ary tree node can have between 0 to N child nodes. N-ary trees are used in various use cases but moreover, these are useful where we are required to represent hierarchical data with multiple branching points at each level, for example, family trees, file system directories, etc.
N-ary Tree in Data Structures
The N-ary Tree allows a node to have up to N children, unlike Binary Trees which allow only up to 2 children nodes. Generic trees are usually used where multiple branching is required at each level like in family trees, decision trees, organizational charts, etc.
To implement an N-ary tree we can use multiple data structures such as arrays, linked lists, dynamic arrays, etc. Different data structures have their advantages and disadvantages.
Example
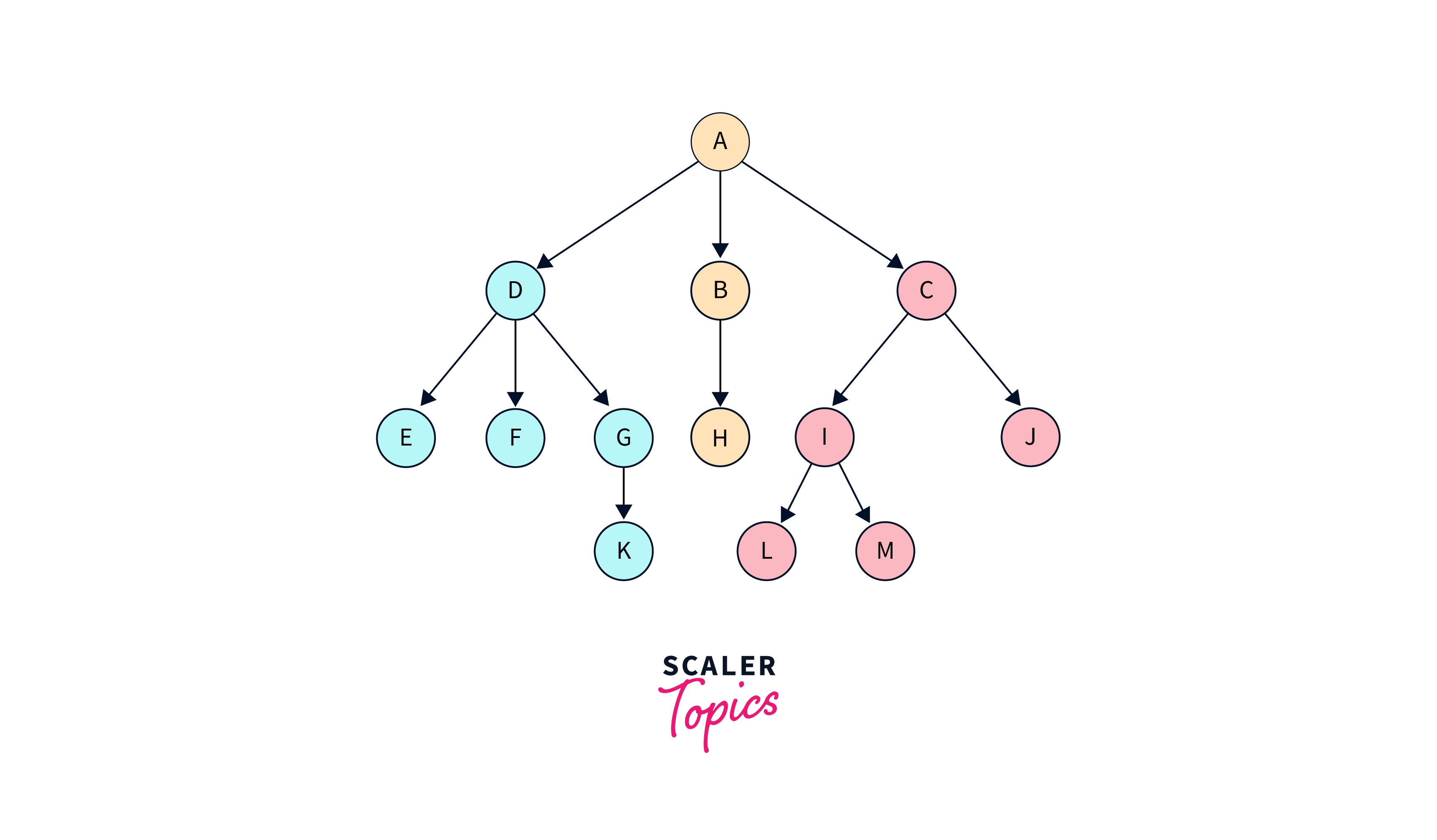
Let us look at an example of an N-ary tree with N = 3. All the nodes have at most three children. We cannot predict how many child nodes are connected to a given node.
Basic Approach
The primary approach to implement N-array is using LinkedList or Arrays. We will store the data of the current node and address it to all of its child nodes.
What to store stored:
- the value of the current node
- address of all its children nodes.
We can build a class or structure to store data and addresses. Here, to store the addresses we can either use an array or a LinkedList.
- Array:
Arrays are fixed-size data structures. Even if the node has no children, space for six addresses will be occupied as in the case of leaf nodes. This is very inefficient if N is large, the depth of the tree is greater as compared to the width, or the number of child nodes differs too much. - LinkedList:
If we will use LinkedList then we will only have to store the address of the first child of the node. But random access to children is not possible, we are required to traverse the LinkedList to get to any child except first. The space complexity of the tree reduces but in the worst case, to access a child node time complexity increases to O(N).
Improved Approach
To improve the shortcomings of arrays and LinkedLists we can use dynamic arrays like ArrayList or vectors. The shortcoming of the array is resolved, if we have the child node then only we reserve the space as memory allocation is dynamic. The shortcoming of the LinkedList is also resolved, we can use indexing to access the child nodes in dynamic arrays.
Implementation
We can create a new class called N_aryNode. This class has an integer data value and a vector that will store the address to all of its child nodes.
CPP:
class N_aryNode {
int value;
vector<TreeNode*> childNodes;
};
Java:
class N_aryNode {
int value;
ArrayList<TreeNode> childNodes;
};
Most Efficient Approach for N-ary Tree in Data Structure
The above given method is better than the naive approach but we can still improve the performance of the N-ary Tree. The optimal approach can be where each node stores the data, the address of its first child, and the address of the next sibling.
We won’t be using an array to store all the child nodes of the parent node. Parent will only store the address of the first child node and this node can be used to get to other child nodes. Therefore, it is also called First Child / Next Sibling Representation.
The node stores the following information:
- Data value
- Address of the first child
- Address of the next sibling
Implementation
To implement the above First child/ Next sibling representation we will create a class called N_aryNode. It will have three properties data, nextSibling, and firstChild.
CPP:
struct Node {
int data;
Node *firstChild;
Node *nextSibling;
};
Java:
class Node{
int data;
Node firstChild;
Node nextSibling;
}
Advantages of Using this Approach
- Reduced Space Complexity:
The brute force approach stores pointers to all of its child nodes. This consumes a lot of space, especially if the tree is sparse (i.e., nodes have varying numbers of children). In contrast, the first child / next sibling representation only requires two pointers per node, majorly reducing memory consumption. - Easier Traversal:
This approach makes the Traversal of an N-ary more straightforward and efficient. It is easy to traverse in any order, such as, preorder, inorder, or postorder. We can easily move to the first child or the next sibling without requiring to iterate through an array of pointers. - Improved Insertions and Deletions:
Insertions and Deletions are comparatively very efficient in the case of first child / next sibling representation. In the case of arrays, if we wish to insert or remove a node in between then we are required to shift the rest of the nodes. This is not the case here, we can simply add a new node and make it point to the next sibling. The parent-child-sibling representation makes the updation of the tree quick and simpler without affecting the rest of the nodes. - Better Cache Performance:
The first child / next sibling representation can be more cache-friendly in accessing nodes and their data since related nodes (first child, and next sibling) are likely to be stored close to each other in memory, improving cache locality. - Dynamic Sibling Management:
Unlike arrays we can insert siblings in any order in this representation. With the next sibling pointer, we can efficiently manage the order of siblings while inserting or removing a node without having to reorder.
FAQs
Q. What are the advantages of using the first child-next sibling representation in N-ary trees?
A. The first child-next sibling representation offers advantages such as reduced space complexity, efficient traversal, simplified insertions and deletions, better cache performance, and dynamic sibling management.
Q. Why might the naive approach be suitable for certain scenarios?
A. The naive approach can be suitable when the tree structure is relatively fixed, and memory usage is not a significant concern. In such cases, it can be straightforward to implement and work with.
Q. Can you efficiently insert or delete nodes in an N-ary tree using the first child / next sibling representation?
A. Yes, inserting or deleting nodes can be more efficient with this representation compared to the naive approach. You can easily update the parent’s “first child” and “next sibling” pointers to perform insertions and deletions without extensive pointer manipulation.
Conclusion
- N-ary Tree or Generic Tree is a tree that can have several child nodes in the range of 0 to N. For example, a 5-ary tree can have at most 5 child nodes.
- To implement the N-ary tree naive approach use an array that stores the address of all the child nodes.
- The above approach is not very space efficient as even the leaf node occupies an array with N space. Also, it is not suitable for the tree node having a varying number of child nodes.
- Another naive approach uses LinkedList. The LinkedList will store the child nodes. This is also inefficient as to get data of a node we are required to traverse the LinkedList resulting in increased space complexity.
- Considering the drawbacks of using arrays and LinkedList, we can make use of dynamic arrays such as ArrayLists or vectors.
- But a more efficient method is using the first child / next sibling representation of the N-ary Tree.
- In this approach a node stores the data, the pointer to the first child, and the pointer to the next sibling.
- This reduces time complexity, improves space utilization, and also makes insertions and deletions faster, simpler, and in any order.