Problem Statement
Given a binary tree, we need to traverse the tree (visit and print the nodes of the need) without using a stack or recursion.
Note: Use the Morris traversal to traverse the binary tree without using any extra data structure and recursion.
Example
Input tree is:
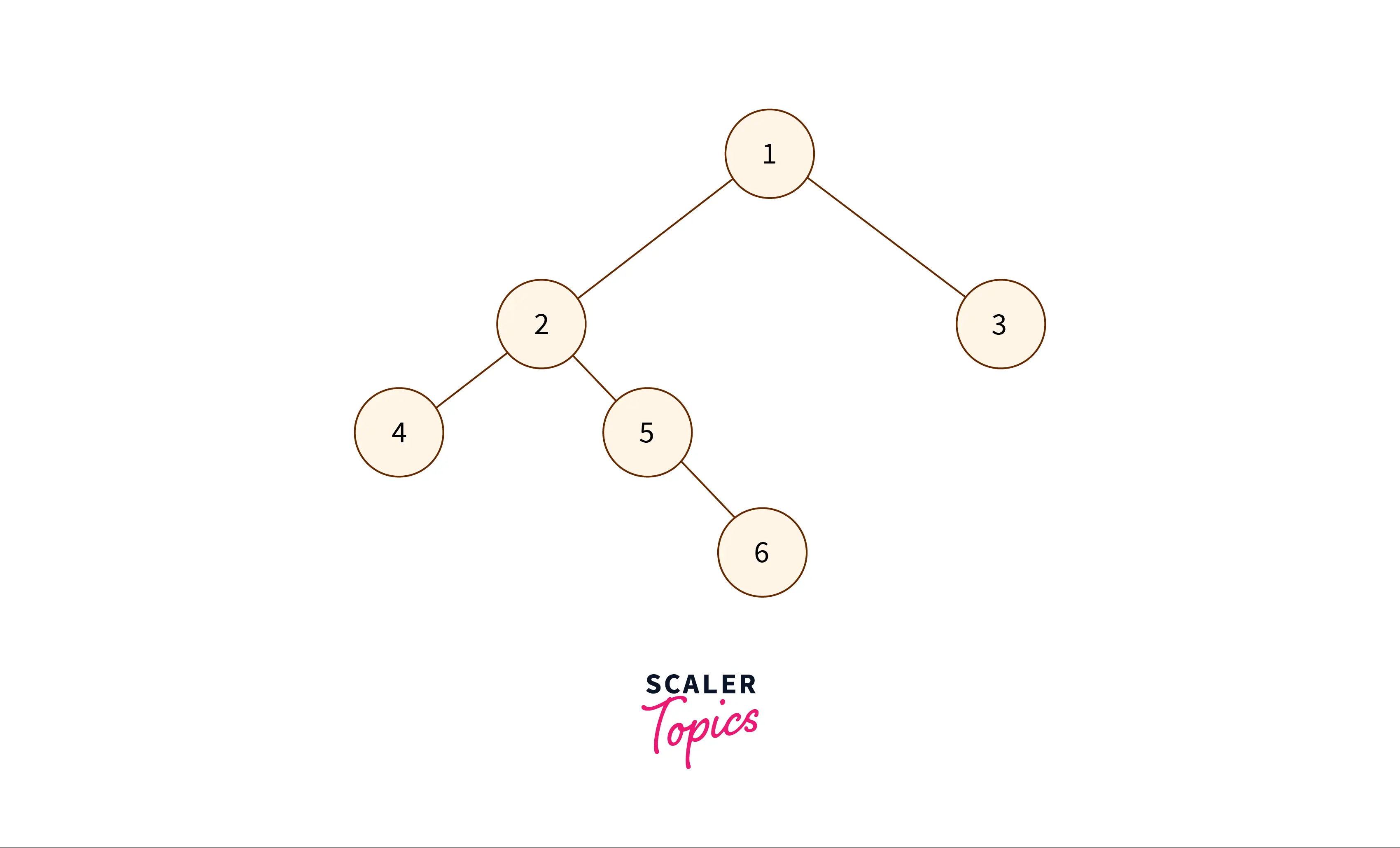
Output: The Morris traversal (in order) of the binary tree is: 4, 2, 5, 6, 1, 3.
Example Explanation
Before getting into the example explanation of how the Morris traversal is performed, let us first get a brief introduction about the in-order and pre-order traversal algorithms as we will be using both of them further.
In the in-order tree traversal we first traverse the left subtree, then the root node, and finally the right subtree. The pseudo-code for the in-order traversal can be:
- If the current node has a left child, recursively visit the left subtree (until NULL is found).
- Visit the root node.
- If the current node has the right child, recursively visit the right subtree (until NULL is found).
On the other hand, in the pre-order tree traversal, we first traverse the root node, then the left subtree, and finally the right subtree.
The pseudo-code for the pre-order traversal can be:
- Visit the root node.
- If the current node has a left child, recursively visit the left subtree (until NULL is found).
- If the current node has the right child, recursively visit the right subtree (until NULL is found).
Let us take the above tree and see how the Morris traversal is performed.
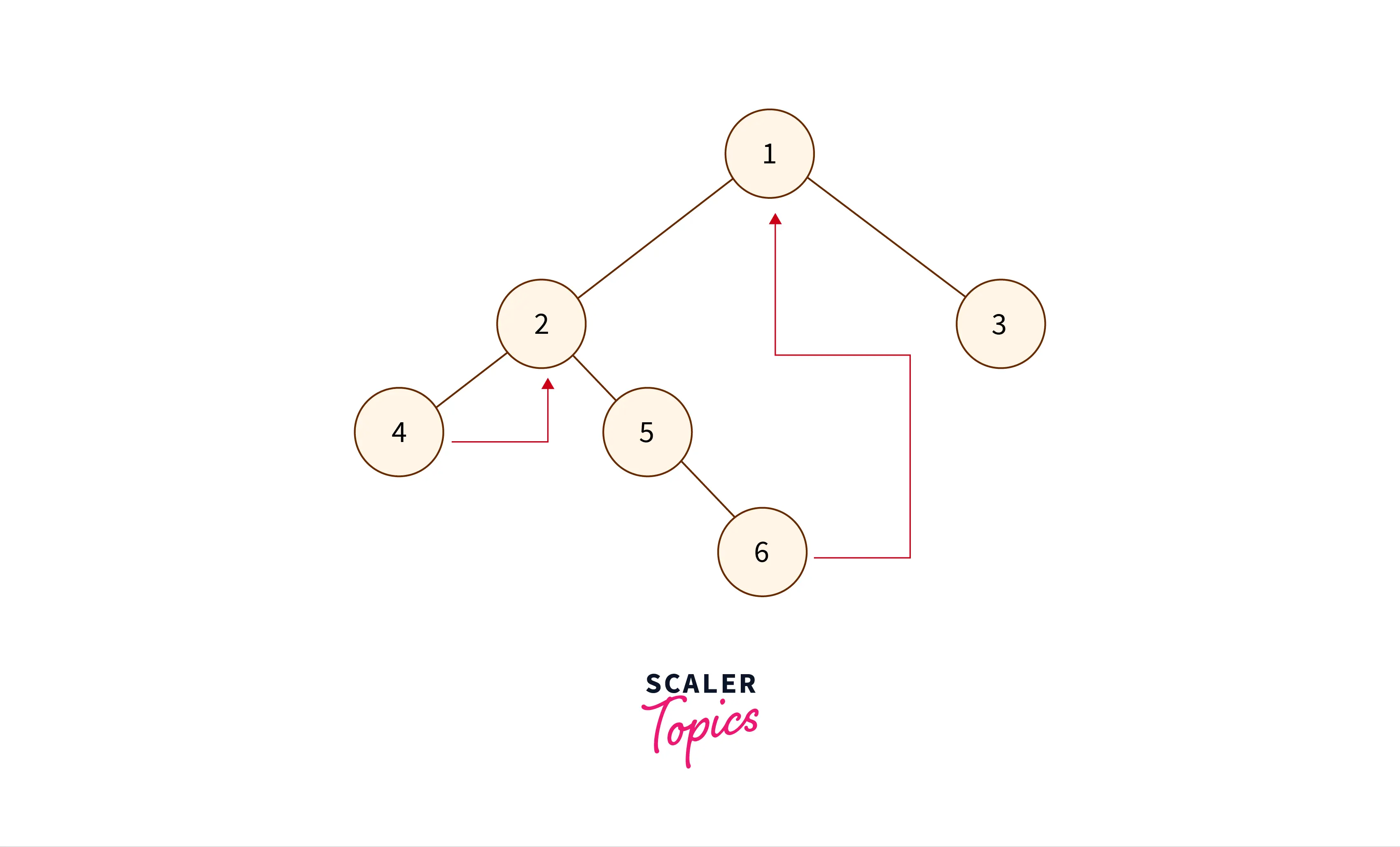
Morris traversal (whether pre-order or in-order or post-order) is performed on a threaded binary tree. A threaded binary tree has a thread or link that points to some ancestor node. Due to this thread linkage, we do not need to use any extra data structure or recursion to traverse the entire tree. Refer to the image provided below to see how the threaded binary tree will look.
Now, if we break the tree into smaller subtrees then we can traverse the tree without using recursion. Let us divide the tree and build the analogy.
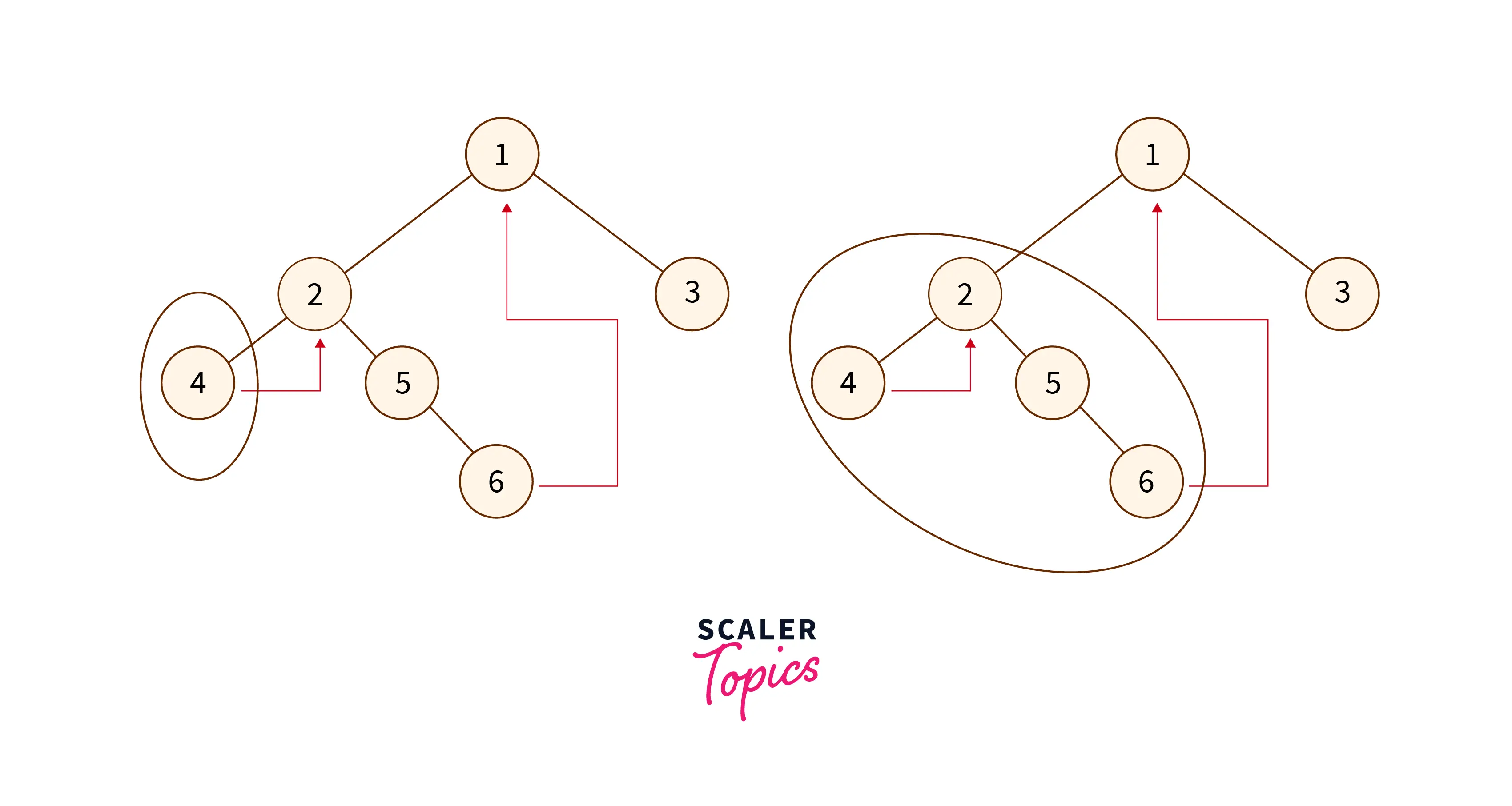
Suppose that we are currently at the node-6, as we can see that the node does not have any left or right child so we can move back to its major parent using thread i.e move back to the node-1. Hence, we do not require any recursive approach, a link is there that will help us to get back to the place where we started.
Note: We can notice that if the current node is the last node of the subtree i.e. its right child is pointing to NULL or None, then we would move back to the parent of the subtree using the thread.
Input/Output
Input: The provided binary tree is:
1
/ \
2 3
/ \
4 5
Output: The Morris traversal (pre-order) of the binary tree is: 1, 2, 4, 5, 3.
Constraints
- 1 <= Number of nodes <= 104
- 0 <= Data of a node <= 105
In some problems, you may find the number of test cases represented by t. So, we only need to call the MorrisTraversal() function t-times.
Algorithm – Morris Traversal for Pre-order Without Using Recursion and Stack
We have already discussed how we can traverse the entire binary tree without using any extra data structure or recursion with the help of the thread binary tree concept. We will create links to the successor nodes and after traversing we will modify the links to get back to the original binary tree.
Let us see the pseudo-code to understand the algorithm better.
Algorithm
- Initialize the root node as the current node (currentNode).
- If the left child of the current node is null then print the data of the current node and move to the right child.
- Else (current node has a left child), make the right child of the in-order predecessor point to the current node.
- Now, if the right child of the in-order predecessor is already pointing to the current node then make the right child NULL and move to the right child of the current node.
- Else (the right child of the in-order predecessor is NULL) then sets the right child as the current node. Now, print the data of the current node and move to the left child of the current node.
- Perform the above-mentioned steps until the current node does not become NULL.
Code Implementation
C++ Code:
#include <bits/stdc++.h>
using namespace std;
// defining the node of the tree.
class Node {
public:
int data;
Node *left, *right;
};
// a function that will add nodes to the tree.
Node *insertNode(int data) {
Node *temp = new Node();
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
// A function that will perform the pre-order Morris traversal without using recursion or extra data structure.
void MorrisTraversal(Node *root) {
// traversing, while the root node does not, becomes NULL.
while (root) {
// When the left child is null, we will print the data and move to the right child
if (root->left == NULL) {
cout << root->data << " ";
root = root->right;
}
else {
/*
Else we will first find the in-order predecessor of the root node and then check the right child of the node.
*/
Node *current = root->left;
while (current->right && current->right != root)
current = current->right;
/*
If the right child of the predecessor points to the root node then make the right child point to null and move to the right child of the root node.
*/
if (current->right == root) {
current->right = NULL;
root = root->right;
}
else {
/*
Otherwise, print the data of the root and make the right child of the predecessor point to the root node. At last move to the left child of the root node.
*/
cout << root->data << " ";
current->right = root;
root = root->left;
}
}
}
}
int main() {
Node *root = NULL;
root = insertNode(1);
root->left = insertNode(2);
root->right = insertNode(3);
root->left->left = insertNode(4);
root->left->right = insertNode(5);
MorrisTraversal(root);
return 0;
}
Java Code:
class Node {
int data;
Node left, right;
Node(int item) {
data = item;
left = right = null;
}
}
public class Main {
// creating the root node
Node root;
// A function that will perform the pre-order Morris traversal without using recursion or extra data structure.
void MorrisTraversal()
{
MorrisTraversal(root);
}
void MorrisTraversal(Node node) {
// traversing, while the root node does not, becomes NULL.
while (node != null) {
// When the left child is null, we will print the data and move to the right child
if (node.left == null) {
System.out.print(node.data + " ");
node = node.right;
} else {
/*
Else we will first find the in-order predecessor of the root node and then check the right child of the node.
*/
Node current = node.left;
while (current.right != null && current.right != node) {
current = current.right;
}
/*
If the right child of the predecessor points to the root node then make the right child point to null and move to the right child of the root node.
*/
if (current.right == node) {
current.right = null;
node = node.right;
}
/*
Otherwise, print the data of the root and make the right child of the predecessor point to the root node. At last move to the left child of the root node.
*/
else {
System.out.print(node.data + " ");
current.right = node;
node = node.left;
}
}
}
}
public static void main(String args[]) {
Main tree = new Main();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.MorrisTraversal();
}
}
Python code:
# defining the node of the tree.
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# A function that will perform the pre-order Morris traversal without using recursion or extra data structure.
def MorrisTraversal(root):
# traversing while the currentNode node does not becomes NULL.
currentNode = root
while currentNode:
# When the left child is null, we will print the data and move to the right child
if currentNode.left is None:
print(currentNode.data, end=" ")
currentNode = currentNode.right
else:
"""
Else we will first find the in-order predecessor of the root node and then check the right child of the node.
"""
previous = currentNode.left
while previous.right is not None and previous.right is not currentNode:
previous = previous.right
"""
If the right child of the predecessor points to the root node then make the right child point to null and move to the right child of the root node.
"""
if previous.right is currentNode:
previous.right = None
currentNode = currentNode.right
else:
"""
Otherwise, print the data of the root and make the right child of the predecessor point to the root node. At last move to the left child of the root node.
"""
print(currentNode.data, end=" ")
previous.right = currentNode
currentNode = currentNode.left
if __name__ == "__main__":
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
MorrisTraversal(root)
Output
1 2 4 5 3
In the Morris traversal, we are traversing the entire binary tree only once. In the traversal, we are not using any extra data structure like a stack. We are following the iterative approach.
Time Complexity
In the Morris traversal, we are traversing the binary tree only once. So, the time complexity of the Morris traversal comes out to be O(n), where n is the size of the binary tree or the number of nodes present in the binary tree.
Space Complexity
In the Morris traversal, we are traversing the binary tree only once and for the traversal, we are not using any extra data structure, we are only using an extra pointer. So, the space complexity of the Morris traversal comes out to be O(1).
Conclusion
- Morris traversal is performed on a threaded binary tree. A threaded binary tree has a thread or link that points to some ancestor node.
- Due to the threaded linkage present in the threaded binary tree, we do not need to use any extra data structure or recursion to traverse the entire tree.
- In the Morris traversal, we create links to the successor nodes, and after traversing we will modify the links to get back to the original binary tree.
- In Morris traversal, we are iteratively traversing the entire binary tree only once. In the traversal, we are not using any extra data structure like a stack.
- The time complexity of the Morris traversal comes out to be O(n), where n is the number of nodes present in the binary tree.
- The space complexity of the Morris traversal comes out to be O(1).