Minimum Number of Jumps to Reach End

You are given with the array of positive integers and asked to find the minimum number of steps or jumps required to reach the end.

Takeaways

Excellent problem to learn time and space complexity optimization in dynamic programming problem.

Problem Statement

The problem statement that is given to us, is —

You are given an array of positive integers, in which each element represents the maximum number of “steps” or “jumps” that you can take from that element. You are required to return the minimum number of steps or jumps required to reach the end of the array. If you cannot reach the end, return -1. At one point in the array, you are only allowed to move forward, and no backtracking is allowed.

As we know, we must minimize these steps taken to reach the end of the array, these steps must be taken starting from the first element of the array, to reach the last element of the array. If at a point in the array, the value of the element is 0, you cannot move further from the point, which means that the end of the array is not reachable. In this case, we return -1.

Example

To understand the problem statement better, let’s take a few examples.

• Example 1
  Input: [2, 3, 1, 1, 4]
  Output: 2
• Example 2
  Input: [2, 3, 0, 1, 4]
  Output: 2
• Example 3
  Input: [1, 3, 5, 8, 9, 2, 6, 7, 6, 8, 9]
  Output: 3
• Example 4
  Input: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
  Output: 10

Example Explanation

Example 1

In this case, the path we would follow for jumps would start from index 0, moving 1 step (the maximum number of steps that can be taken is 2, we can take 1) to index 1. From index 1, we can take a maximum of 3 steps, and in 3 steps we can reach the last index. Hence, we jump from index 1 to index 4. Therefore, the total number of jumps or steps required to reach the last index is 2.

If we take 2 steps from index 0, we land on index 2. From index 2, we can take just 1 step to index 3, and it is a similar case for index 3. This approach would take us 3 jumps from the starting index of the array to reach the end of the array.

Example 2

For this case, we will start from index 0, from which we can take a maximum of 2 steps. If we take 2 steps, we land on index 2 which is 0. From index 2 we cannot take more steps, making the end of the array unreachable. Instead, we will take just one step to index 1. At index 1, we can take 1, 2, or 3 steps. If we take 1 step, we land on index 2, which is again 0. If we take 2 steps, we would have to take another extra step to reach the end of the array. Hence, we take 3 steps and land at index 4, i.e. the end of the array making the total number of jumps = 2.

Example 3

In this case, from the element at index 0, we have just 1 possibility, which is to take 1 step. At index 1, we have the option of taking either 1, 2 or 3 steps. If we chose either of the options at index 3 or 4 (i.e. the numbers 8 or 9) we can reach the end of the array. Hence, the total number of jumps required in this array is just 3.

Example 4

All the elements of this array are the same and equal to 1. This means that at every stage we can take just 1 step. Hence, to reach the end of the array, we would take 10 jumps.

Constraints

1 <= array.length <= 10^4
0 <= array[i] <= 1000

The length of the array given as input would always be greater than or equal to 1, and less than or equal to 104104, and every element in the array would be a positive integer with a value less than or equal to 1000.

Approach 1: Naive Recursive Approach

Let us now try to formulate an approach to solve the problem at hand. The brute force solution or the naive solution would be to try out all cases and select the one that has taken the minimum number of jumps as our solution.

If we take the example 1 array – [2, 3, 1, 1, 4], we would try out all the possible cases i.e., from index 0, we would go to index 1 and index 2. From index 1, we would try taking the jump to index 2, 3, 4 and so on.

Here’s what all the possible cases would look like: 

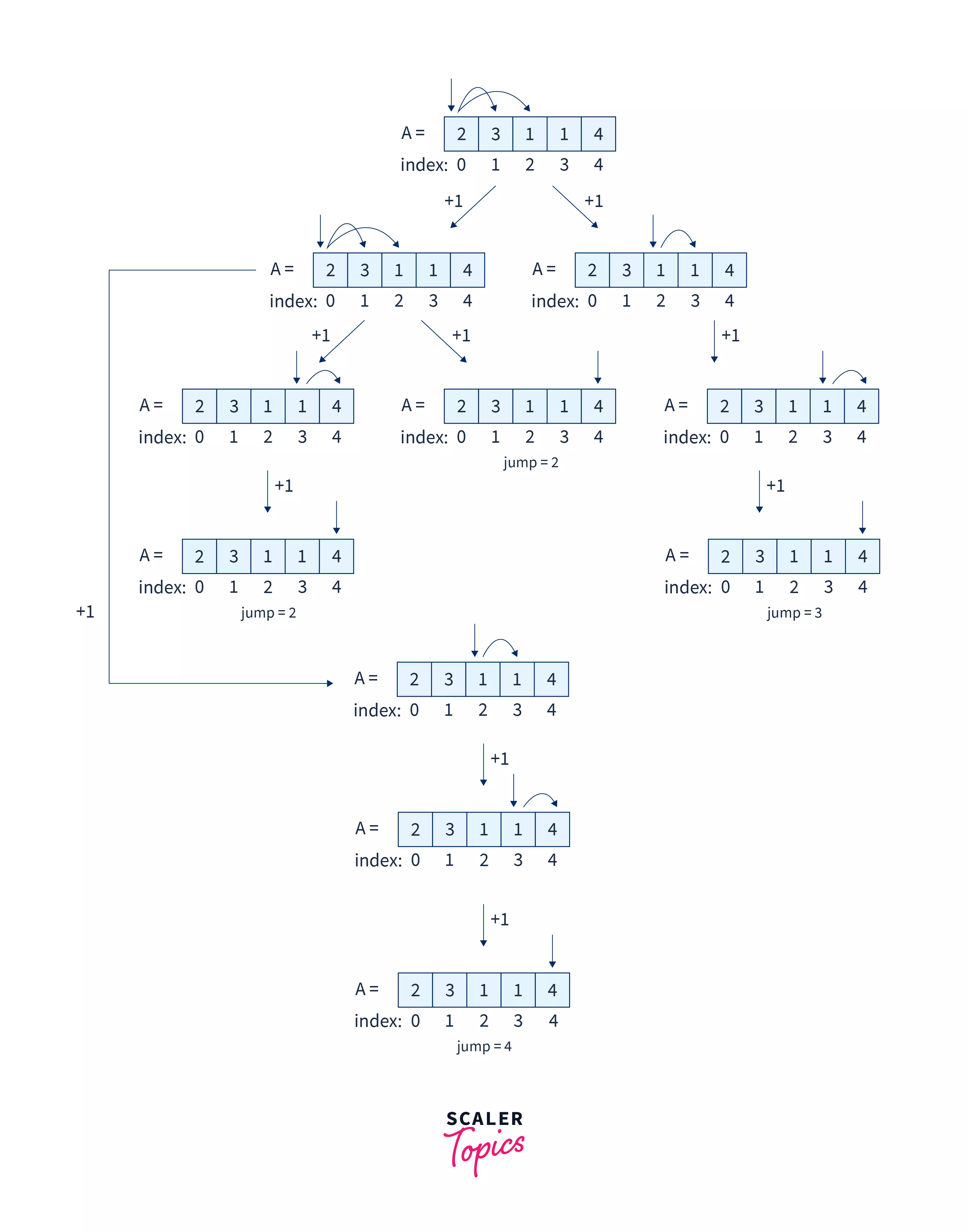
So, now we know that our naive solution would be to test out all possible cases and find out the case that gives us minimum jumps. But how? Let’s think!

Since we require testing all possible cases, we can apply the concept of recursion — finding the solution to a larger problem by dividing it into smaller problems and using the solution of the smaller problems to come to a final solution. Say our function is – min_jumps(array, start, end) where start and end are the starting and ending indices. We can call our function (from all cases), initially as – min_jumps(array, 0, length), and then recursively on the number of possibilities from that index.

For this recursive function, the base case would be that our current index is the last index, and our recursive case would be to loop over the possible cases from the current index to reach the end of the array, and find the minimum number of jumps possible from all cases possible.

Algorithm:

So, we know our algorithm – we’re going to create a function that will be called recursively. We start from the first element of the array at index 0 and then recurse the function for each step (the maximum that can be taken from that index) till the current step > 0. Post that, the value must be minimized for each iteration. Finally, we will return the minimum number of jumps required to reach the end of the array.

Pseudocode for this algorithm:

function min_jumps(array, index):
	if index = length of array then
		return 0
	jumps <- infinite
	// looping from 1 to the maximum number of steps that can be taken from that index
	for steps = 1 to array[index] do:
		if index + steps are less than the length of the array then:
			next <- min_jumps(array, index + steps)
			jumps <- min(jumps, next + 1)
	return jumps

Code implementation in C/C++:

int min_jumps(vector<int> array, int index){
	// storing size of array in variable n
	int n = array.size();
	// if nothing is possible from source, return -1
	if (array[0] == 0)
		return -1;
	// if the maximum possible jumps are greater than size of array, return 0 jumps.
	if (index >= n)
		return 0;
	// initializing jumps to 1 more than maximum possible jumps 
	int jumps = 10001;
	// looping from 1 to maximum jumps possible from that index 
	for (int i = 1; i < array[index]; i++){
		// finding minimum of current jumps and recursive call to index + i-th position in array
		// adding 1 since we are taking a jump from current index to index + i
		jumps = min(jumps, 1 + min_jumps(array, index + i));
	}
	return jumps;
}

Code implementation in Java:

static int min_jumps(int array[], int index){
	// storing size of array in variable n
	int n = array.length();
	// if nothing is possible from source, return -1
	if (array[0] == 0)
		return -1;
	// if the maximum possible jumps are greater than size of array, return 0 jumps.
	if (index >= n)
		return 0;
	// initializing jumps to 1 more than maximum possible jumps 
	int jumps = 10001;
	for (int i = 1; i < array[index]; i++){
		// finding minimum of current jumps and recursive call to index + i-th position in array
		// adding 1 since we are taking a jump from current index to index + i
		jumps = min(jumps, 1 + min_jumps(array, index + i));
	}
	return jumps;	
}

Python implementation:

def minJumps(array, index):
	if array[0] == 0:
		return -1
	if index >= len(array):
		return 0
	jumps = 10001
	for i in range(1, array[index] + 1):
		jumps = min(jumps, 1 + minJumps(array, index + i))
	return jumps

Complexity Analysis

Let us now analyze the time and space complexities of this approach to find the minimum number of jumps.

Time Complexity

To analyze the time complexity of this problem, let’s first understand that there are a maximum of ‘m’ possible ways to move from one index where m is the maximum value inside the array (taking an upperbound). So for every position in the array, we have ‘m’ choices, and if we have ‘n’ elements in the array, our time complexity would be – $m_1 * m_2 * … * m$_n.

Time complexity –O(m^n)(exponential)

Space Complexity

In terms of space, we use a single variable that holds the value of jumps, and hence the space complexity is constant – O(1).

Space complexity – O(1).

Approach 2: Dynamic Programming

In the above approach, take a look at the diagram depicting all possible jumps. A critical point that you would notice, is that there are certain sub-problems, that are overlapping. We are solving certain small problems again and again, that are affecting our time complexity and increasing it. To optimize this, we will apply a dynamic programming approach, which works by storing the results of sub-problems so that they do not have to be calculated multiple times.

To understand how to solve 1-dimensional dynamic programming problems in detail, you can refer to this article by scaler topics on solving 1-dimensional DP problems as well as this one on 2-dimensional DP problem solving. However, to understand this problem, you do not need to have a solid understanding of DP.

Some of the overlapping sub-problems can be seen in this figure:

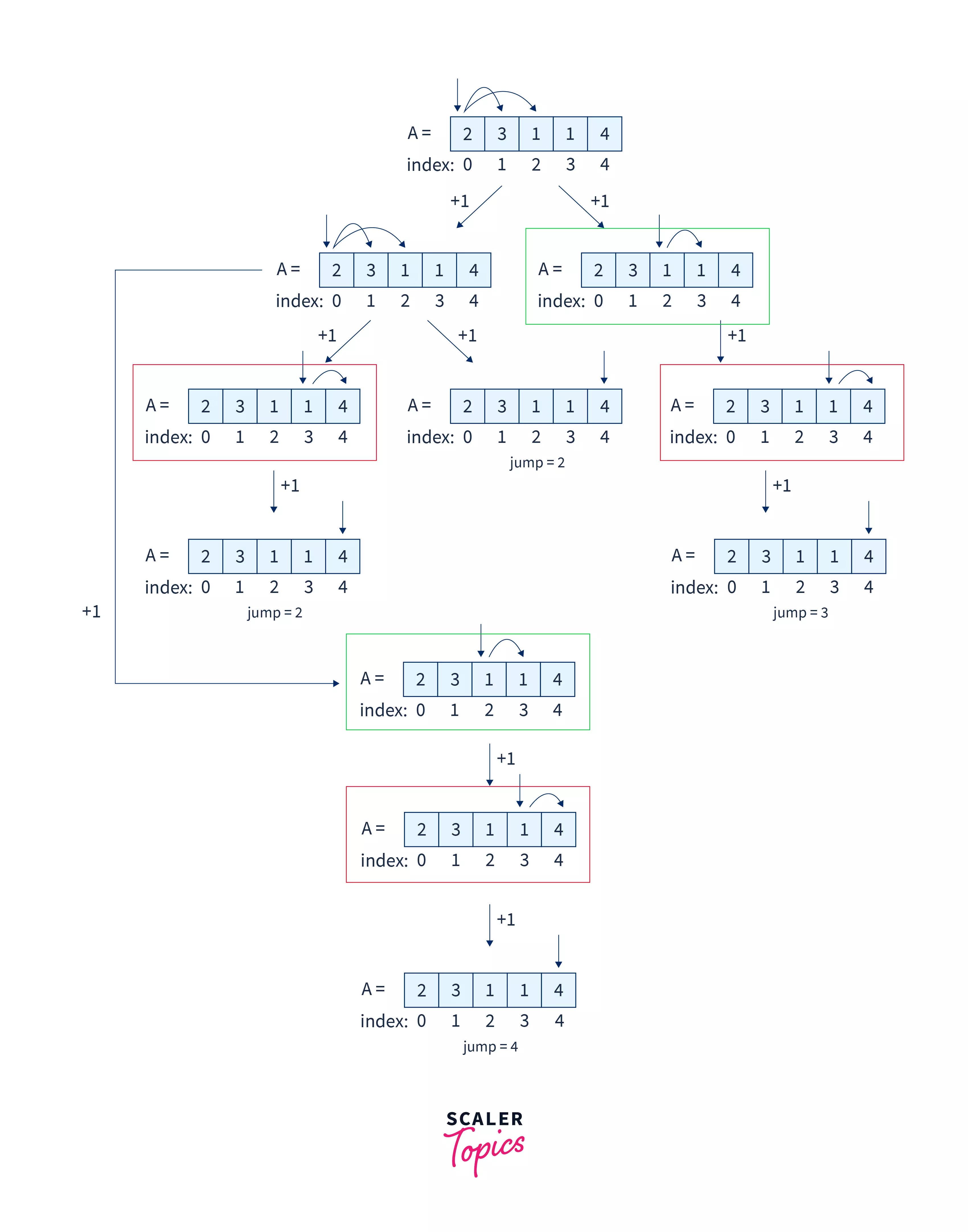
Since we know that this problem can be solved using the concept of dynamic programming, we can apply the bottom up approach to this problem. Our aim would be to store the results of these smaller overlapping sub-problems in an iterative manner in a table.

• Table size:
  Since we have just one variable – jumps, that decreases by 1 in the recursion, we can use a 1-dimensional array – jumps of size n where n is the number of sub-problems. Every element in this array – jumps, i.e. jumps[i] would indicate the minimum number of jumps/steps that are required to reach array[i] from the start index.
• Initializing the table:
  To initialize the table, we will simply put jumps[0] as 0, since 0 steps are required to get to the 0th index from the 0th index. The rest of the values will depend on the values calculated for the next ones. So, we will start to calculate the number of jumps required in every possible case and fill in the minimum value of jumps required found in the range [i + 1, i + array[i]].
• To fill up the table, we will use an iterative manner and our final answer will be stored at the index n - 1, i.e. last index of the new jumps array.

Algorithm:

The algorithm that we will follow is –

• First we will create an array of size n called dp, where n is the size of our current given array as input. All the elements except the first one will be initialized to INT_MAX or 10001 (as per constraints, no value in the array will be higher than 10000). Every element of the dp array, i.e. dp[i] will represent the minimum number of jumps required to reach the ith index in the original array.
• First element of this array dp will be 0, i.e. dp[0] = 0.
• The recursive structure of our problem to fill up the dp array would be:
  dp[i] = 1 + min(dp[i], 1 + min(dp[i + 1], dp[i + 2], ..., dp[i + dp[i] + 1]))
• Next we will iterate from 0 to n - 1, and run a nested loop from i + 1 (where i is outer loop variable) till min(arr[i] + 1, n) to find the minimum of dp[i] and i + dp[i].
• After all the iterations, simply return the value of dp[n - 1].

Code implementation of the above approach in C++:

int min_jumps(vector<int> array){
	int n = array.size();
	// handling the edge case
	if (n == 0 || array[0] == 0)
		return -1;
	// creating dp vector
	vector<int> dp(n, 10001);
	// initializing first element as 0 since it takes 0 jumps to reach 0th index
	dp[0] = 0;
	for (int i = 0; i < n; i++){
		for (int j = i + 1; j < min(i + array[i] + 1, n)){
			// dp[j] will contain minimum jumps required to reach j index in array
			dp[j] = min(dp[j], 1 + dp[i])
		}
	}
	return dp[n - 1];
}

Code implementation in Java:

int min_jumps(int[] array){
	int n = array.length;
	// handling the edge case
	if (n == 0 || array[0] == 0)
		return -1;
	// creating dp vector
	int dp[] = new int[n];
	// initializing first element as 0 since it takes 0 jumps to reach 0th index
	dp[0] = 0;
	for (int i = 0; i < n; i++){
		for (int j = i + 1; j < min(i + array[i] + 1, n)){
			// dp[j] will contain minimum jumps required to reach j index in array
			dp[j] = min(dp[j], 1 + dp[i])
		}
	}
	return dp[n - 1];
}

Code implementation in Python:

def minJumps(array):
	n = len(array)
	# creating the dp array, and initializing all values to 10001 according to constraints
	dp = [n] * 10001
	# first element is 0 since number of jumps required to reach this index is 0
	dp[0] = 0
	# looping over array
	for i in range(n):
		# looping over number of jumps possible from index
		for j in range(i + 1, min(i + num[i] + 1, n)):
			dp[j] = min(dp[j], dp[i] + 1)
	# returning last value of dp array
	return dp[n - 1]

Complexity Analysis

This solution works better than the previous brute force approach. How? Let’s see.

Time Complexity

As you can observe in the code, we are using two ‘for’ loops that iterate over the input array. So, the time complexity of this program is majorly the time complexity of the nested ‘for’ loops. Hence, time complexity = $O(n^2)$.

Space Complexity

This solution slightly differs from the previous solution in terms of space complexity, since we create a new array, the dp array of size n. Hence, space complexity = $O(n)$.

Approach 3: Greedy Approach

Can we improve the time complexity of the previous approach, which was O(n^2), to linear i.e. O(n)?

Yes, of course! We’re going to make use of a greedy approach to improve the time complexity. How? The main idea is to continue moving ahead in the array as long as we can. If we are at a point in the array where we cannot move, we’ll jump from the particular element in the array that will take us as far as possible, among all the elements that we have visited. Not clear? Read on.

In the dynamic programming approach to finding the minimum number of jumps possible, we observed that from a certain position ‘i‘, the maximum jump that you can make is to position array[i] + i. Take a look at the diagram below:

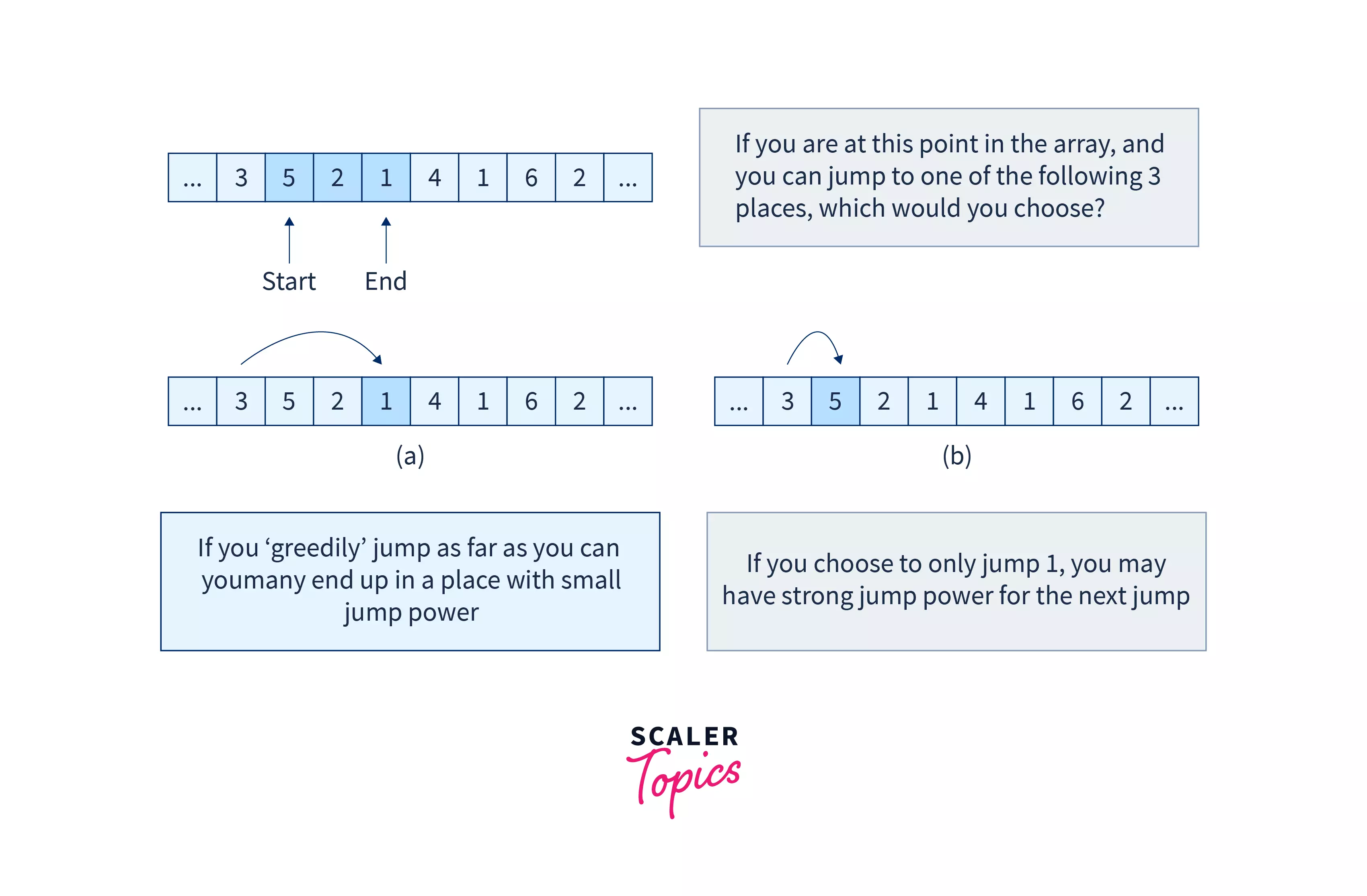
As you can see, the first index of the array has a value of 3 which means that the maximum index that can be reached from this index is 3 + 0 = 3 (array[i] + i). The values that can be reached from this index are – 5, 2 and 1. From index 3, we need to take a jump that will allow us to reach the farthest end of the array. Which one would you choose?

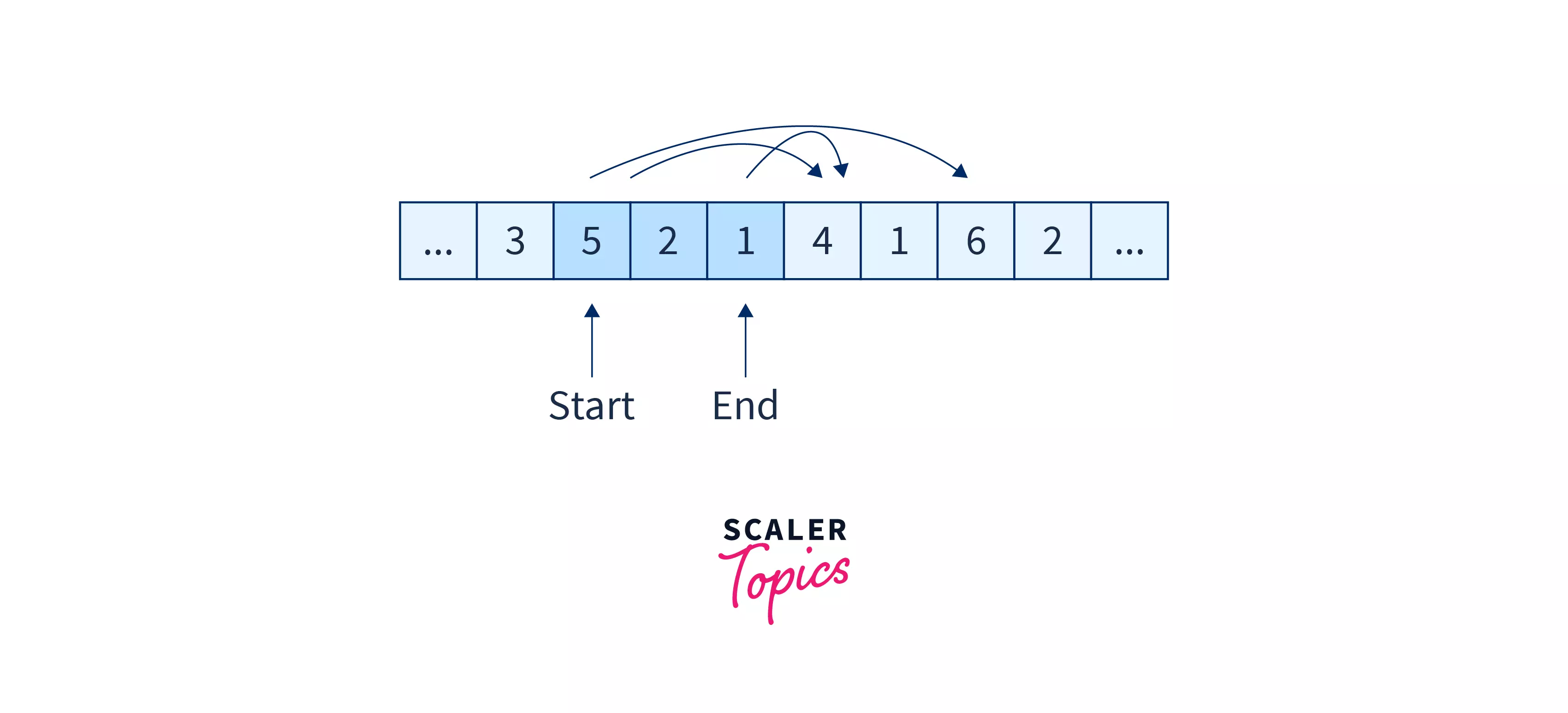
According to the greedy approach, we will choose to go to index 1 from index 0, which will take us to index 6, i.e. the farthest in the array. So here’s the algorithm that we follow.

Algorithm:

• First, we will create 3 variables that will store values of the current number of jumps taken, a variable that stores the end of the array, and another variable that tells us the farthest that we can go. Initially, the value of all these variables is 0.
• Iterate over the input array and find out the farthest end that can be reached. If the farthest end that can be reached is the end of the array, return total jumps.

Pseudocode:

function minJumps(array):
	n <- length of the array
	farthest <- 0
	jumps <- 0
	i <- 0
	while i < n do:
		// i + array[i] denotes the farthest point you can reach from ith index
		farthest = max(farthest, i + array[i])
		if i is equal end:
			jumps <- jumps + 1
			end <- farthest
	return jumps

Code implementation in C++:

int minJumps(vector<int> array){
	int n = array.size();
	int jumps = 0, currJumpEnd = 0, farthest = 0;
	for (int i = 0; i <= n; i ++){
		farthest = max(farthest, array[i] + i);
		if (i == currJumpEnd){
			jumps++;
			currJumpEnd = farthest;
		}
	}
	return jumps;
}

Code implementation in Java:

int minJumps(int[] array){
	int n = array.length;
	int jumps = 0, currJumpEnd = 0, farthest = 0;
	for (int i : array){
		farthest = max(farthest, array[i] + i);
		if (i == currJumpEnd){
			jumps++;
			currJumpEnd = farthest;
		}
	}
	return jumps;
}

Code implementation in Python:

def minJumps(array):
	jumps = 0
	currJumpEnd = 0
	farthest = 0
	for i in range(len(array) - 1):
		farthest = max(farthest, array[i] + 1)
		if i == currJumpEnd:
			jumps += 1
			currJumpEnd = farthest
	return jumps

Complexity Analysis

This approach works faster than our previous approaches, let’s analyze the time complexity.

Time Complexity

Time complexity: O(n)

As our code uses just one loop, we essentially iterate over all the elements in the array just once, and hence our time complexity would be O(n) where n is the number of elements in the array.

Space Complexity

Space complexity: O(1)

Since in this approach we are not creating an array like the previous approach, the space complexity of this approach is O(1) – constant.

Conclusion

• The problem statement that is given to us, is – You are given an array of positive integers, in which each element represents the maximum number of “steps” or “jumps” that you can take from that element. You are required to return the minimum number of steps or jumps required to reach the end of the array. If you cannot reach the end, return -1.
• There are 3 approaches to solve this problem:
  • Brute Force – recursive
  • Dynamic Programming
  • Greedy Approach