There is a well-known problem Maximum Subarray Sum, in which we have to find a contiguous subarray whose sum is maximum among all the subarrays for the given array. To solve this one must know about Kadane’s Algorithm. Kadane’s Algorithm is an iterative dynamic programming algorithm.
Scope of Article
This article gives detailed information about Kadane’s Algorithm.
This article also gives a brief introduction to dynamic programming, which is a very important topic.
This article also shows the Brute Force solution for the famous Maximum Subarray Sum problem.
Definition
Kadane’s Algorithm is an iterative dynamic programming algorithm ( A method that is often used to solve finite-dimensional nonlinear constrained global optimal control problems ), so to understand Kadane’s Algorithm we need to understand Dynamic Programming first. Kadane’s Algorithm is used to solve the famous problem – Maximum Subarray Sum. This Algorithm is used to solve the problem in linear time.
What is a Sub-Array?
We know that an array is a contiguous memory block. Similarly, a sub-array is any contiguous part of that array, which may consist of any number of elements with atleast one element in it.
Let us write all the subarrays for the array: [‘a’,’b’,’c’,’d’]
The sub-arrays for this array are:
| Index of element | Subarrays possible |
| :—: | :- |
| 0 -> ‘a’ | {‘a’}, {‘a’, ‘b’}, {‘a’, ‘b’, ‘c’}, {‘a’, ‘b’, ‘c’, ‘d’} |
|1 -> ‘b’ |{‘b’}, {‘b’, ‘c’}, {‘b’, ‘c’, ‘d’} |
|2 -> ‘c’| {‘c’}, {c’, ‘d’} |
|3 -> ‘d’|{‘d’}|
Total number of subarrays possible in an array of length N = N.(N+1)/2
Dynamic Programming
Dynamic Programming : Those who cannot remember the past are condemned to repeat it.
Dynamic Programming refers to simplifying a complex problem by breaking it down into simpler sub-problems. It basically breaks the problem recursively and solves each sub-problem, and stores each solution in a memory-based data structure (eg. map, array, dictionary). Then using the optimal solutions for each sub-problem, we come up with the optimal solution for the whole problem.
Dynamic Programming is a huge topic on its own. So, for this article we just need the basic concept of it, that is storing the solutions of sub-problems, and reusing it.
Maximum Subarray Problem
After learning about dynamic programming, let’s now dive into the Maximum Subarray Problem.
So, What is this Maximum Subarray Problem?
The main motive of this problem is to find a sub-array from an array, whose sum is maximum among all the sub-arrays and return that maximum sum. You must be thinking that, maximum sum will be the sum of all elements in the array, but if there are negative numbers also in the array, then the answer might not be the same.
For Example:
Let the array be: [2, -4, 3, -1, 2]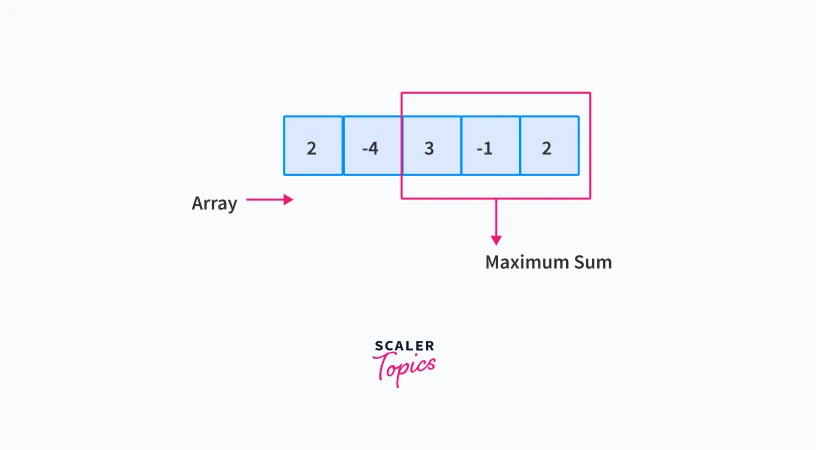
In this array, the subarray with maximum sum is [3, -1, 2] with sum 4, whereas the total sum of the array is 2.
Brute Force Approach
After knowing what is Maximum Subarray problem, dynamic programming, now let’s try to solve this problem with a brute force solution.
Suppose you ask a school kid to solve this problem with any approach he wants. So the kid will do is, that he will write all the possible subarrays and count the sum for each subarray and then find the maximum of all those.
This approach by the kid is called a brute-force approach, which is trying all possible outcomes, and then finding the maximum of all.
To define this brute-force approach, we will start with the element at index 0, and then calculate the sum of every subarray possible for that element. Then we will start with the element at 1st index, and calculate the sum of every subarray possible for that element, and so on we will check all the subarrays.
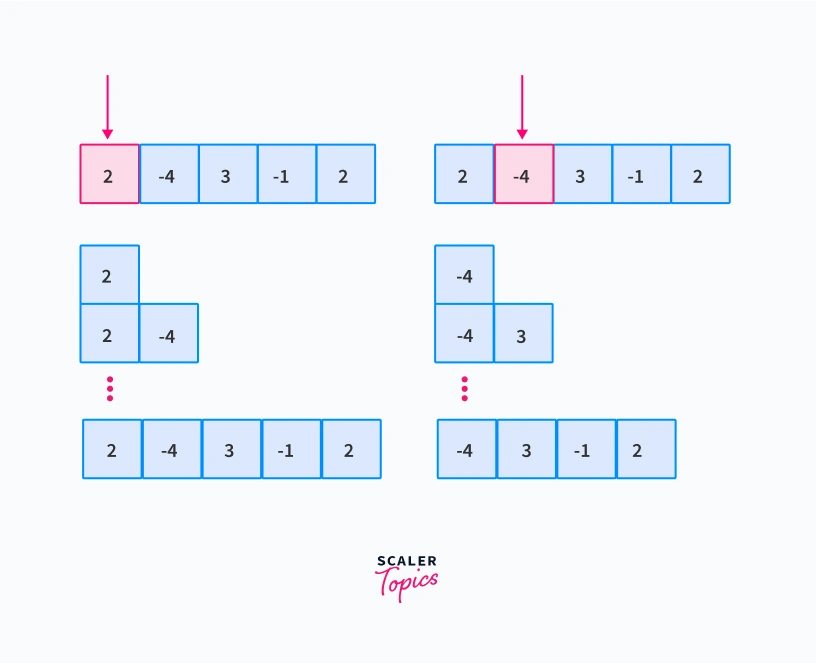
This approach basically checks all possible subarrays, which means if the size of array is n then the time-complexity of this algorithm would be O(n²), thus taking huge time to execute.
Proof: We know that there are $n*(n+1)/2$ number of subarrays for an array with n elements, so our brute-force algorithm will search for all the subarrays, thus running almost $n^2$ times. Thus it has a complexity of O($n^2$).
What is Kadane’s Algorithm ?
Now after seeing the brute-force solution, you must be thinking about how to optimize this approach. So, to optimize the solution, we will be using the concept of dynamic programming here. Kadane’s Algorithm is an example of dynamic programming algorithm, which uses the solutions of previous sub-problems to find the overall optimum solution.
Now let’s dive into the working of Kadane’s algorithm.
Working of the Algorithm
In Kadane’s Algorithm, we look for all positive contiguous subarrays of the array, keeping track of the global maximum sum which will be the array. Whenever we get a positive-subarray-sum, we compare it with the global_max and update global_max if the sum is greater than the global_max, and whenever we get a negative-subarray-sum, we have to reset the sum to zero, because we will never take that element for the next subarrays.
Initialize:
local_max = 0
global_max = INT_MIN
For each element we will follow these steps:
- local_max = local_max + a[i]
- if (local_max > global_max )
set global_max = local_max - if (local_max < 0)
set local_max = 0
global_max is the maximum sum required.
Lets understand the above algorithm using an example.
Let the array be: [2, -4, 3, -1, 2]
at first,
local_max = global_max = 0
Now, lets loop through each element.
when i=0, a[0]= 2:
local_max = local_max + 2 = 2.
since, local_max is greater than global_max, so set global_max = 2.
when i=1, a[1]= -4:
local_max = local_max + (-4) = 2+(-4) = -2
since local_max < 0, we wll set local_max to 0.
but, global_max is still 2.
when i=2, a[2]= 3:
local_max = local_max + (3) = 0+3 = 3
since local_max(= 3) > global_max(= 2)
so we will set global_max = 3.
when i=3, a[3]= -1
local_max = local_max + (-1) = 3+(-1) = 2
global_max is still greater than local_max, so no update will be done here, i.e. global_max = 2
when i=4, a[4]= 2
local_max = local_max + 2 = 2+2 = 4
since local_max(= 4) > global_max(= 2),
we will set global_max = 4.
Thus we get the maximum subarray sum as 4
Note:
The above algorithm will fail for the case, when there are only negative elements in the array, because our global_max is already set to 0. So, to handle that case we have to modify our algorithm. We will add current element to the previous subarray only if it results in a greater sum, else we will start the new subarray from that element.
Approach:
Initialize:
local_max = 0
global_max = INT_MIN
For each element we will follow these steps:
- if (a[i] <= local_max + a[i])
local_max = local_max + a[i] - else
local_max = a[i] - global_max = max(global_max, local_max)
global_max is the maximum sum required.
Analysing the above approach, we can write a recursive formulation for Kadane’s algorithm.
local_max[i] = max( A[ i ], A[ i ] + local_max[ i-1 ] )
resulting answer will be the maximum of all the values of local_max[i]
Thus we can see that Kadane’s algorithm has optimal substructure property, which means that for calculating a maximum subarray ending at a particular position, we have to use the solution of a smaller subproblem (the maximum subarray sum ending at the previous position). Thus we can say that Kadane’s Algorithm is a dynamic programming algorithm.
Code for Kadane’s Algorithm
After learning the working of Kadane’s algorithm, let’s dive into the implementation of it for various languages.
- global_max will store the resulting answer
- local_max will get updated after every element, for the local maximums.
C
#include <stdio.h>
#include <limits.h>
int max(int a, int b)
{
if(a>b)return a;
return b;
}
int main()
{
int a[]={2, -4, 3, -1, 2};
int local_max = 0;
int global_max = INT_MIN;
int i;
int n=sizeof(a)/sizeof(a[0]);
for(i = 0; i < n;i++)
{
local_max = max(a[i], a[i] + local_max);
if(local_max > global_max)
{
global_max = local_max;
}
}
printf("%d",global_max);
return 0;
}C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a[]={2, -4, 3, -1, 2};
int local_max = 0;
int global_max = INT_MIN;
int n=sizeof(a)/sizeof(a[0]);
for(i = 0; i < n;i++)
{
local_max = max(a[i], a[i] + local_max);
if(local_max > global_max)
{
global_max = local_max;
}
}
cout<<global_max;
return 0;
}Java
import java.util.*;
import java.lang.*;
import java.io.*;
class KadanesAlgo
{
public static void main (String[] args) throws java.lang.Exception
{
int a[]={2, -4, 3, -1, 2};
int local_max = 0;
int global_max = Integer.MIN_VALUE;
int n=a.length;
for(int i=0;i<n;i++)
{
local_max = Math.max(a[i], a[i] + local_max);
if(local_max > global_max)
{
global_max = local_max;
}
}
System.out.println(global_max);
}
}Time Complexity
Time Complexity of Kadane’s Algorithm is O(n)
The way this algorithm uses optimal substructures, this algorithm can be seen as simple dynamic programming. This algorithm traverses the whole array only once, so the time complexity depends on the length of the array linearly.
Note:
To print the subarray also, we have to maintain the indices of start and end whenever the global_max updates.
Initialize:
local_max = 0
global_max = INT_MIN
start = 0 end = 0 s = 0
For each element we will follow these steps:
- if( a[i] <= local_max + a[i])
local_max = local_max + a[i] - else
local_max = a[i]
s = i - if( global_max < local_max)
global_max = local_max
start = s end = i
The subarray will start from start index, and end at end index, with sum global_max.
Summary
- Kadane’s Algorithm is a Dynamic programming algorithm.
- We can prove this by seeing that, at each step, we have 2 choices: either take the current value and add it to the previous sum OR restart the sum from the new element.
- It is a great optimization over the brute-force solution, as it decreases the time complexity from O(n^2^) to O(n).