Problem statement:
Given two strings string_1 and string_2 of size N and M respectively. Find the length of the longest common substring.
The problem statement says that we are given two strings and we need to return the length of the longest common substring from the given strings. For example:
Input:
string_1 = "fishes"
string_2 = "fisherman"
Output:
5
Explanation:
The longest common substring from string_1 and string_2 of lengths N = 6 and M = 9 respectively, is “fishe” and it is of length 5. Therefore the output is 5. Let’s discuss various ways for obtaining the length of the longest common substring.
Constraints:
- 1<N<104
- 1<M<104
- where N and M are the lengths of the string_1 and string_2 respectively.
What is a Substring?
A substring is the contiguous sequence of characters within the given string. For example, “string” is a substring of “substring” where the order remains the same. For instance, Consider given input string is “abce” The substrings of the given string are:
[a, b, c, e, ab, bc, ce, abc, bce, abce]
A substring is contiguous, unlike a subset. Even the whole string is also considered to be one of the substrings of the given string. If N is the length of the given string, then the number of non-empty substrings from the given string is calculated by:
Number of non-empty substrings = (N*(N+1))/2 Now as we have a basic understanding of substring let’s discuss the longest common substring. When two strings are given we need to find the length of the longest substring among these two strings. For instance, consider
string_1 = "acevd"
string_2 = "acenbvd"
The common substrings among these two strings are:
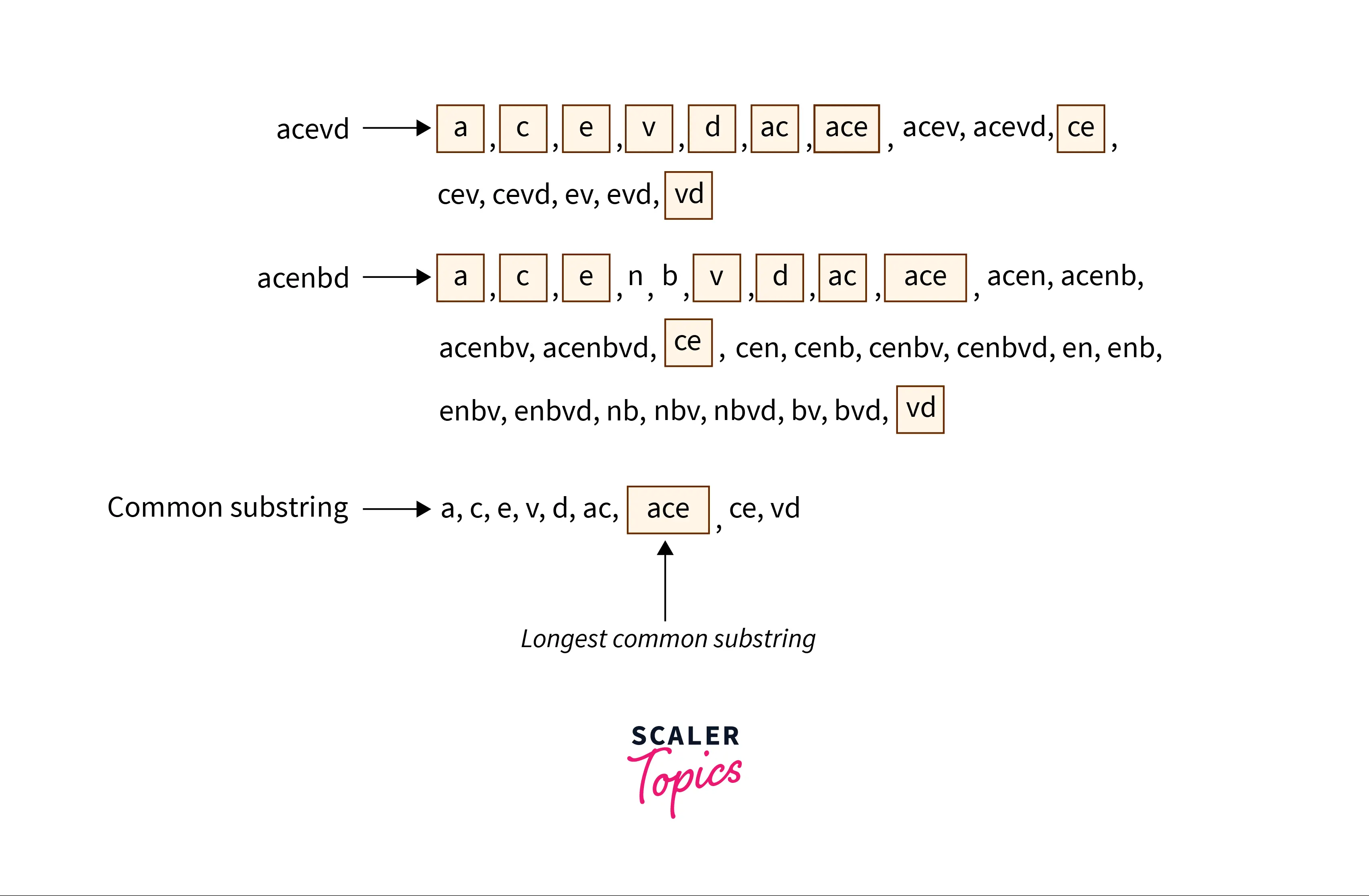
But the longest common substring is “ace” of length 3.
Approach 1 (Brute Force Approach):
Algorithm:
- Generate all the substrings of string_1 and string_2 using three nested loops and store them in any data structure like an array.
- For generating substrings we use three nested loops:
- The outer loop keeps track of starting character
- The second loop tracks all the characters on the right of the starting character as the ending character of the substring.
- The innermost/third loop appends the characters from the current starting index to the ending index.
- Therefore generating substrings takes a time complexity of O(N^2) where N is the length of the strings given.
- Now from the substrings from the arrays, compare each substring of each string given and always carry forward the maximum length of the common substring formed from the given two strings.
- Return the length of the longest common substring obtained.
Implementation:
Since this is a naive approach we can just follow the algorithm and create all the substrings and compare for the length of the longest common substring from the given strings.
Complexity Analysis:
Time Complexity: O(N^2 * M^2) where N and M are the lengths of the string_1 and string_2 respectively.
- For generating the substrings for string_1 and string_2 and comparing the formed substring one by one.
- Here, string_1 has N^2 number of substrings and string_2 has M^2 number of strings.
- For comparing all these formed substrings of string_1 and string_2, it takes O(N^2^ * M^2^).
- Therefore the overall time complexity is O(N^2 * M^2)
Space Complexity: O(N^2) + O(M^2) where N and M are the lengths of the string_1 and string_2 respectively.
- For storing the substrings formed by each string.
- string_1 takes O(N^2^) space and string_2 takes O(M^2^) and the sum of it is the space complexity.
Approach 2: Efficient Approach using Recursion
The above approach generates all the substrings of given strings and compares iteratively. Instead of redundantly creating all the substrings, we can just use recursion for comparing the strings. If the character at which we are checking is matched then, we increment the LCSCount by 1 else, making it 0.
Algorithm:
This algorithm uses recursion for finding the length of the longest common substring from the given two strings. The algorithm is as follows:
- Start traversing from the end of the two strings with i and j for string_1 and string_2 respectively using recursion.
- If the last characters of both the strings match then decrement both the iterators by 1 and increment LCSCount by 1 and store it in LCSCount_1.
- Else, we need to consider the following two cases:
- Just decrement the iterator of string_1 and call the recursive function by updating LCSCount to 0 (because we missed the contiguous character of the string) and store it in LCSCount_2.
- The other way can be decrementing the iterator of string_2 by 1 and again calling the recursive function by updating the LCSCount to 0 and store it in LCSCount_3
- The base case of this function would be till iterator_1 and iterator_2 should be greater than zero, else return the LCSCount because once any one of the iterators becomes zero it means that we have come to an end of the string given and there can be no further longest common substring which will be formed so, we need to return the LCSCount.
- The answer in this approach is the maximum of LCSCount1, LCSCount_2, LCSCount_3.
This recursive relations can be better explained using:
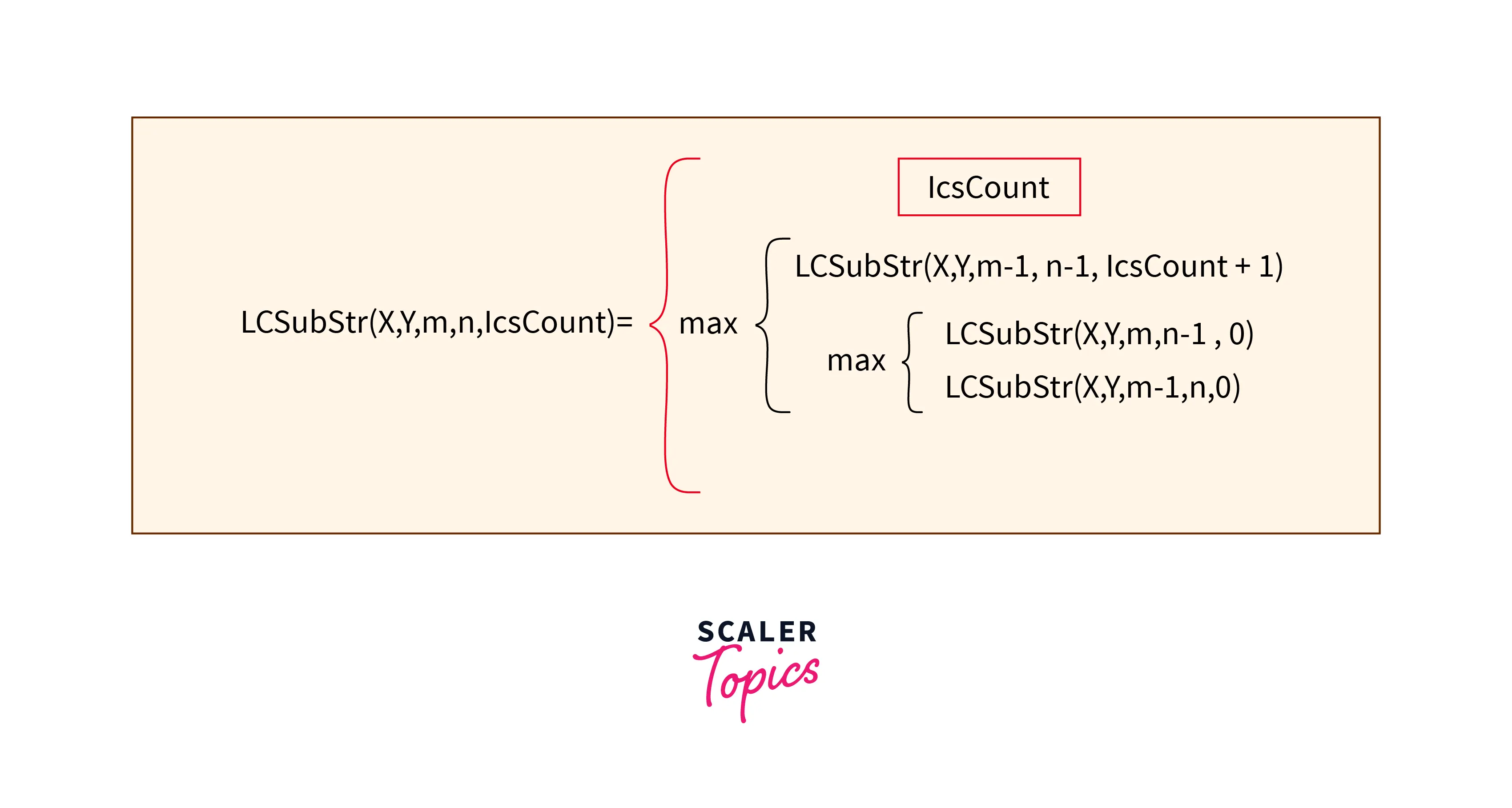
Implementation:
Below is the implementation of the above approach:
C++ implementation for finding the length of the longest common substring using recursion:
// C++ program for finding the length of the longest common substring using recursion
#include <iostream>
using namespace std;
string string_1, string_2;
// This is the recursive function that returns the length of the longest common substring
int LCS(int iterator_1, int iterator_2, int LCSCount){
// Base Case
if (iterator_1 == 0 || iterator_2 == 0)
return LCSCount;
// If the last character is same then the next character need to be compared to decrement the counter
// increase the LCSCount by 1
if (string_1[iterator_1 - 1] == string_2[iterator_2 - 1]) {
LCSCount = LCS(iterator_1 - 1, iterator_2 - 1, LCSCount + 1);
}
// if the characters are not the same then you need to decrease the iterator_1 once and update the LCSCount to 0
// The other case can be we can decrement the iterator_2 and update the LCSCount to 0
// The answer is the max of all these cases
LCSCount = max(LCSCount, max(LCS(iterator_1, iterator_2 - 1, 0),LCS(iterator_1 - 1, iterator_2, 0)));
// return the LCSCount
return LCSCount;
}
// Driver code
int main(){
int N, M;
string_1 = "singer";
string_2 = "singing";
// length of two strings is
N = string_1.size();
M = string_2.size();
// call for the recursive function to get the length of the longest common substring
cout << LCS(N, M, 0);
return 0;
}
Output:
4
Python implementation for finding the length of the longest common substring using recursion:
# Python program for finding the length of the longest common substring using recursion
# This is the recursive function which returns the length of the longest common substring
def LCS(iterator_1, iterator_2, LCSCount):
# Base Case
if (iterator_1 == 0 or iterator_2 == 0):
return LCSCount
# If the last character is same then the next character need to be compared to decrement the counter
# increase the LCSCount by 1
if (string_1[iterator_1 - 1] == string_2[iterator_2 - 1]):
LCSCount = LCS(iterator_1 - 1, iterator_2 - 1, LCSCount + 1)
# if the characters are not the same then you need to decrease the iterator_1 once and update the LCSCount to 0
# The other case can be we can decrement the iterator_2 and update the LCSCount to 0
# The answer is the max of all these cases
LCSCount = max(LCSCount, max(LCS(iterator_1, iterator_2 - 1, 0), LCS(iterator_1 - 1, iterator_2, 0)))
# return the LCSCount
return LCSCount
# Driver code
if __name__ == "__main__":
# Given two strings are
string_1 = "singer"
string_2 = "singing"
# length of two strings is
N = len(string_1)
M = len(string_2)
# Call the recursive function by passing the parameters
print(LCS(N, M, 0))
Output:
4
Java implementation for finding the length of the longest common substring using recursion:
// Java program for finding the length of the longest common substring using recursion
class Main{
static String string_1, string_2;
// This is the recursive function which returns the length of the longest common substring
static int LCS(int iterator_1, int iterator_2, int LCSCount){
// Base Case
if (iterator_1 == 0 || iterator_2 == 0){
return LCSCount;
}
// If the last character is same then the next character need to be compared to decrement the counter
// increase the LCSCount by 1
if (string_1.charAt(iterator_1 - 1) == string_2.charAt(iterator_2 - 1)){
LCSCount = LCS(iterator_1 - 1, iterator_2 - 1, LCSCount + 1);
}
// if the characters are not the same then you need to decrease the iterator_1 once and update the LCSCount to 0
// The other case can be we can decrement the iterator_2 and update the LCSCount to 0
// The answer is the max of all these cases
LCSCount = Math.max(LCSCount, Math.max(LCS(iterator_1, iterator_2 - 1, 0), LCS(iterator_1 - 1, iterator_2, 0)));
// return the LCSCount
return LCSCount;
}
// Driver code
public static void main(String[] args){
// length of two strings is
int N, M;
// Given two strings are
string_1 = "singer";
string_2 = "singing";
N = string_1.length();
M = string_2.length();
// call for the recursive function to get the length of the longest common substring
System.out.println(LCS(N, M, 0));
}
}
Output:
4
Explanation: The longest common substring from the string_1 and string_2 of lengths N=6 and M=7 respectively, is “sing” and it is of length 4. Therefore the output is 4.
Complexity Analysis:
Time Complexity: O(3^(N+M)) where N and M are the lengths of the string_1 and string_2 respectively.
- Since we are calling the recursive function three times and checking for all characters until the base case is not achieved.
- A recursive tree is formed which is: // change the values in the recursive tree put n-1, m-1 generic values.
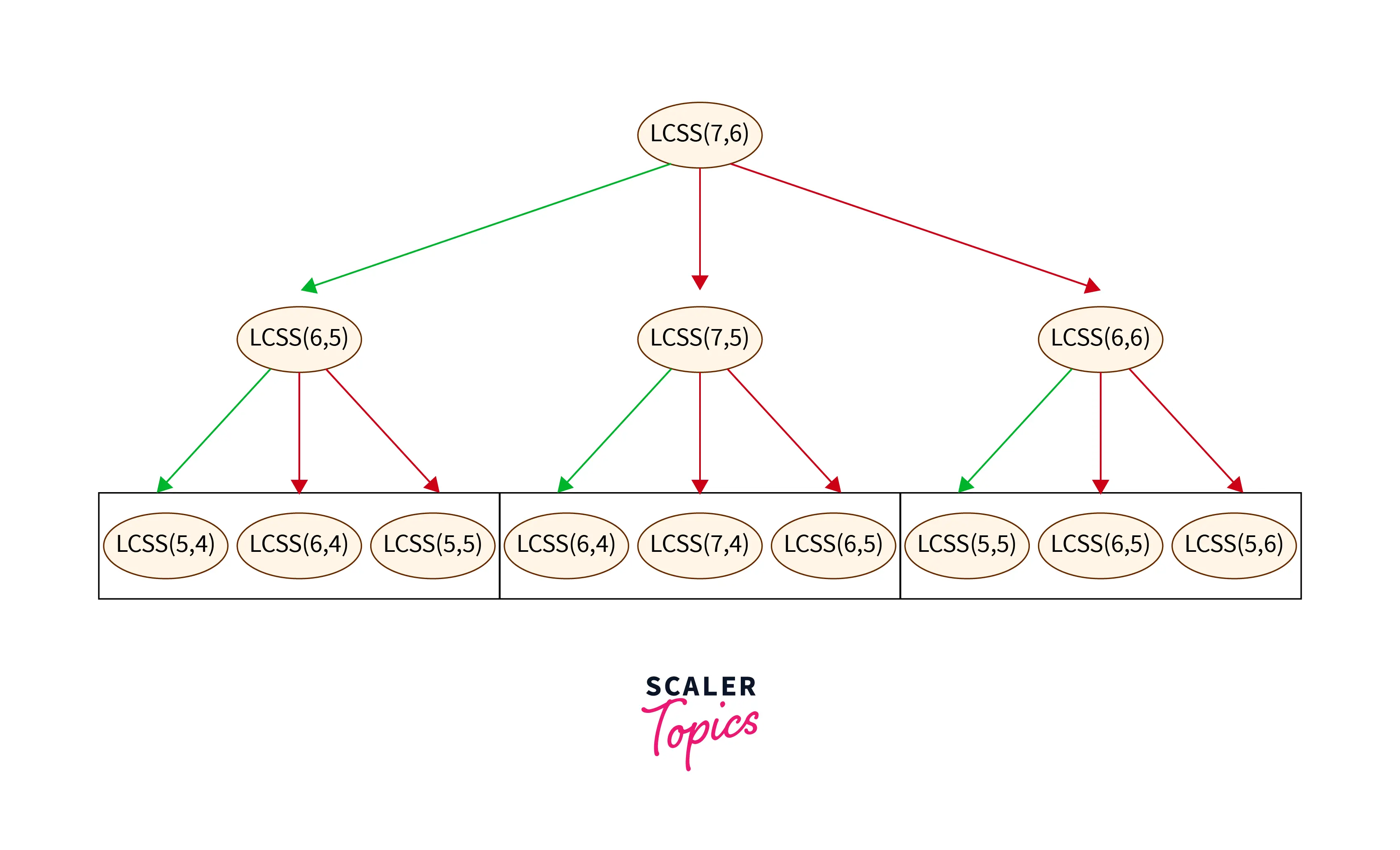
Space Complexity: O(N+M) where N and M are the lengths of the string_1 and string_2 respectively.
- Since the recursive function takes a space of N+M for auxiliary stack space during recursion.
As we can observe in the recursive tree that the sub-problems are called, again and again, this is the situation of overlapping subproblems which can be resolved by using Dynamic programming. The next approach is explained using Dynamic programming to find the length of the longest common substring.
Approach 3: Dynamic programming
This approach uses dynamic programming for finding the length of the longest common substring as it is considered to be more efficient in case of overlapping sub-problems for finding the length of the longest common substring. This dynamic programming uses a bottom-up approach to fill up the table. Here, bottom-up approach first focuses on solving the smaller problems at the fundamental level and then integrating them into a whole and giving the complete solution.
Algorithm:
Dynamic programming is achieved by the tabulation method which uses a 2-D array and stores the length of the longest common substring. This table is filled up in a bottom-up manner.
- Firstly initialize the 2-D array (DP table) with the size [N+1][M+1]. All the values are initialized to 0.
- We use one-based indexing as the first row and the first column is 0.
- This can be done using both iteratively (tabulation) or using memoisation.
- Iterative approach is discussed below.
- For filling the values in the table DP. Here dp[i][j] means that the length of the longest substring which ends at ithith character in string_1 and at jthjth character in string_2, and we need to take the maximum of all of these combinations. For filling up the DP table, we must follow the below algorithm:
- Start two nested loops:
- First loop with iterator i and second loop with iterator j.
- If the characters at string_1[i] matches with string_2[j] then the value at dp[i][j] will be equal to the sum of the dp[i-1][j-1] (diagonal value) + 1.
- This means that the previous characters of both the strings are also matched and we can increase the LCSCount in the present cell. Therefore the top left diagonal store the count of the length of the longest common substring, until that point.
- Else the value at dp[i][j] is zero because the string cannot be consecutive i.e, it is not a part of the matching substring. So, we make the present cell value zero.
- Return the maximum element in the table after formation that is considered to be the length of the longest common substring for the given two strings because each cell represents the length of the longest matching substring till that point.
For a clear understanding of this approach, let’s consider an example: Input:
string_1 = "acdefb"
string_2 = "nbgacde"
By following the algorithm mentioned above the DP table obtained is:
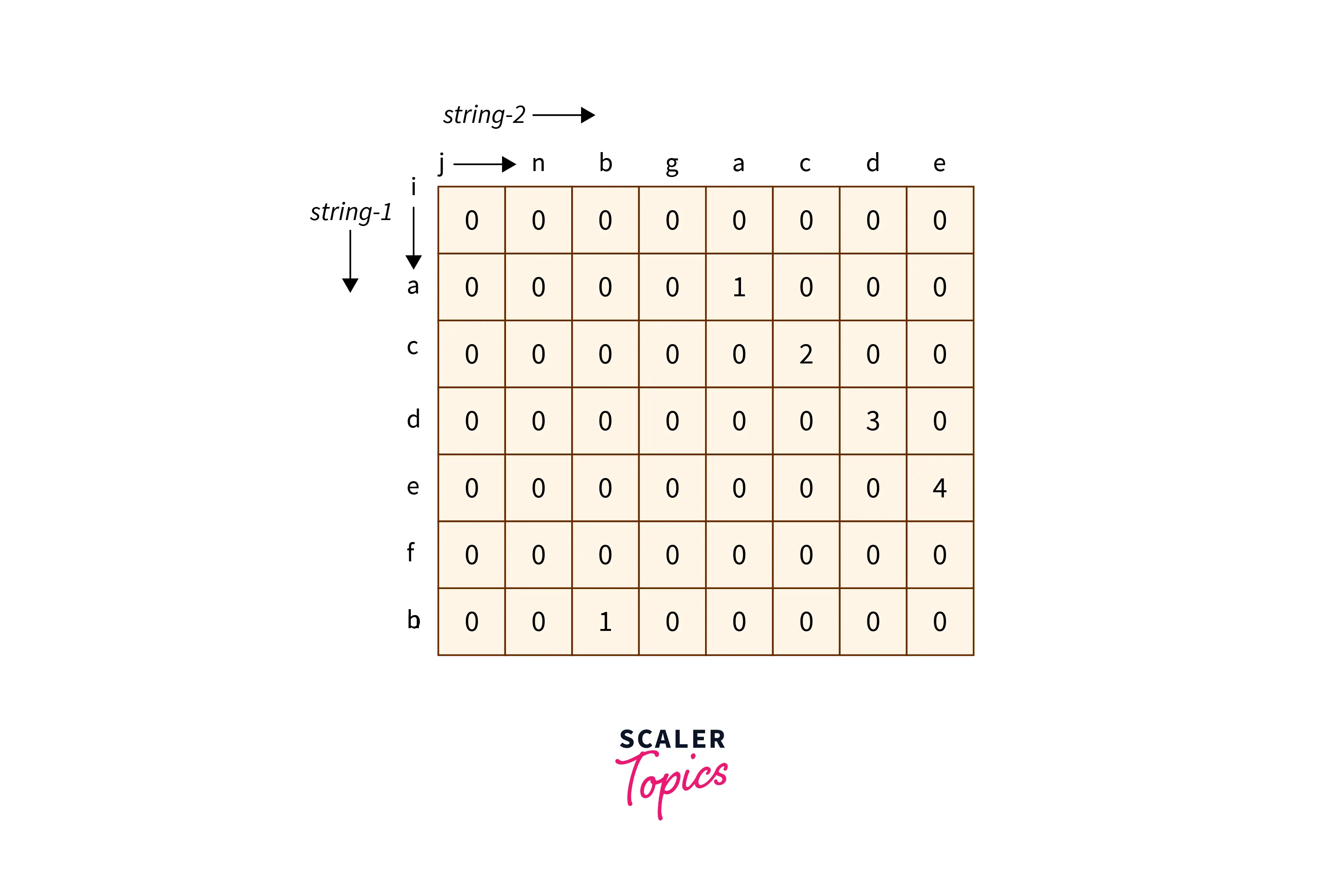
In the table, we can observe that the row represents string_1 and the column represents string_2. Values in the table are filled accordingly. We can observe that the maximum element in the table is 4, which is the length of the longest common substring which is “acde”.
Output:
4
Implementation:
Below is the implementation of this approach:
C++ implementation for finding the length of the longest common substring using Dynamic programming:
// C++ program for finding the length of the longest substring using Dynamic Programming
#include <iostream>
#include <string.h>
using namespace std;
// function which returns the length of longest common substring
int LCS(char* string_1, char* string_2, int M, int N){
// This table keeps track of the substrings which are common
// and contains the length of the longest substring.
// Row in this table represents the string_1 and the column as string_2.
// create a 2-D array named dp and intitialise all the values as zero.
int dp[M + 1][N + 1];
// To store length of the longest
// common substring
int LCSCount = 0;
// Following steps to fill the values in the dp array in bottom-up manner
// Iterative approach for filling the values.
// row iterates over the first string
for (int i = 0; i <= M; i++){
// coloumn iterates over the second string
for (int j = 0; j <= N; j++){
// Base Case
if (i == 0 || j == 0)
dp[i][j] = 0;
// if the characters at string_1 and string_2 matches
else if (string_1[i - 1] == string_2[j - 1]){
dp[i][j] = dp[i - 1][j - 1] + 1;
// carry forwarding the maximum element in the table
LCSCount = max(LCSCount, dp[i][j]);
}
else
// if the characters did not match then the values is zero
dp[i][j] = 0;
}
}
// return the maximum element in the dp table
return LCSCount;
}
// Driver code
int main(){
// Given two strings are
char string_1[] = "acdefb";
char string_2[] = "nbgacde";
// length of two strings
int M = strlen(string_1);
int N = strlen(string_2);
// call for the LCS function to get the length of the longest common substring
cout << LCS(string_1, string_2, M, N);
return 0;
}
Output:
4
Python implementation for finding the length of the longest common substring using Dynamic programming:
# Python program for finding the length of the longest common substring using dynamic programming
def LCS(string_1, string_2, M, N):
# This table keeps track of the substrings which are common and contains the length of the longest substring.
# Row in this table represents the string_1 and the column as string_2.
# create a 2-D array named dp and intitialise all the values as zero.
dp = [[0 for k in range(N+1)] for l in range(M+1)]
# To store the length of the longest common substring
LCSCount = 0
# Following steps to fill the values in the dp array in a bottom-up manner
# Iterative approach for filling the values.
# row iterates over the first string
for i in range(M + 1):
# column iterates over the second string
for j in range(N + 1):
# Base Case
if (i == 0 or j == 0):
dp[i][j] = 0
# if the characters at string_1 and string_2 matches
elif (string_1[i-1] == string_2[j-1]):
dp[i][j] = dp[i-1][j-1] + 1
# carry forwarding the maximum element in the table
LCSCount = max(LCSCount, dp[i][j])
# if the characters did not match then the values is zero
else:
dp[i][j] = 0
# return the maximum element in the dp table
return LCSCount
# Driver code
if __name__ == "__main__":
# Given two strings are
string_1 = "acdefb"
string_2 = "nbgacde"
# length of two strings is
N = len(string_1)
M = len(string_2)
# Call the LCS function by passing the parameters
print(LCS(string_1, string_2, N, M))
Output:
4
Java implementation for finding the length of the longest common substring using dynamic programming:
// java program for finding the length of the longest common substring using dynamic programming
class Main {
// function which returns the length of longest common substring
static int LCS(char string_1[], char string_2[], int M, int N) {
// This table keeps track of the substrings which are common
// and contains the length of the longest substring.
// Row in this table represents the string_1 and the column as string_2.
// create a 2-D array named dp and intitialise all the values as zero.
int dp[][] = new int[M + 1][N + 1];
// To store length of the longest
// common substring
int LCSCount = 0;
// Following steps to fill the values in the dp array in bottom-up manner
// Iterative approach for filling the values.
// row iterates over the first string
for (int i = 0; i <= M; i++){
// column iterates over the second string
for (int j = 0; j <= N; j++){
// # Base Case
if (i == 0 || j == 0){
dp[i][j] = 0;
}
// if the characters at string_1 and string_2 matches
else if (string_1[i - 1] == string_2[j - 1]){
dp[i][j] = dp[i - 1][j - 1] + 1;
// carry forwarding the maximum element in the table
LCSCount = Integer.max(LCSCount, dp[i][j]);
}
else{
// if the characters did not match then the values is zero
dp[i][j] = 0;
}
}
}
// return the maximum element in the dp table
return LCSCount;
}
// Driver code
public static void main(String[] args){
int M,N;
// Given two strings are
String string_1 = "acdefb";
String string_2 = "nbgacde";
// length of two strings
M = string_1.length();
N = string_2.length();
// call for the LCS function to get the length of the longest common substring
System.out.println(LCS(string_1.toCharArray(),string_2.toCharArray(), M, N));
}
}
Output:
4
Explanation: The longest common substring from the string_1 and string_2 of lengths N=6 and M=7 respectively, is “sing” and it is of length 4. Therefore the output is 4.
Complexity Analysis:
Time Complexity: O(M*N) where M and N are the lengths of the given string_1 and string_2 respectively.
- For filling up the the DP table (2-D array) in a bottom-up manner, it requires a time of O(N*M). Each cell can be filled as zero or using the previous cell value as required.
Space Complexity: O(M*N) where M and N are the lengths of the given string_1 and string_2 respectively.
- DP table (2-D array) is of size [M+1][N+1], so the space occupied is O(M*N).
Since we are updating the values in the table using the values of the previous updates, space optimization can be done to the above approach. This algorithm is discussed in the below approach.
Approach 4: Dynamic Programming- Space Optimization
In the above approach, we are only using the last row( updated value) of the 2-D array, therefore we can optimize the space by using a 2-D array of size 2*(min(N, M)).
Algorithm:
- Algorithm remains the same as filling up of 2-D array but instead of column size as N or M, we instead take 2 because we just need the last row.
- Generally, all the dynamic programming approaches can be optimized by using the DP state where we can use the previous state to get the present state’s value and it can also be done using the location of the answer in the DP matrix formed.
- However, we need to traverse the two strings using two nested loops, for obtaining the length of the longest substring.
- The space optimization is done by :
- if string_1[i – 1] is equal to string_2[j – 1], then
dp[i%2][j] = dp[(i – 1)%2][j – 1] + 1- where dp[i%2][j] represents the present cell and the dp[(i-1)%2][j-1] represents the previous state.
- Here we have taken the value to be mod 2, because since it involves only 2 coloumns, we can just use the mod 2 operation while updating the table values.
- Since, we need to carry forward the maximum element in the table, we can do :
- LCSCount = max(LCSCount, dp[i%2][j]).
- If the characters are not matched, then the present cell value is zero.
- if string_1[i – 1] is equal to string_2[j – 1], then
- At last, return the length of the longest common substring.
Below is the implementation of the space-optimized dynamic programming approach for finding the length of the longest common substring from the given two strings.
Implementation
C++ implementation for finding the length of the longest substring by space optimizing using DP state:
// c++ implementation using dynamic programming for space optimisation
#include <iostream>
#include <string.h>
using namespace std;
// function which returns the length of longest common substring
int LCS(string string_1, string string_2, int M, int N){
// This table keeps track of the substrings which are common
// and contains the length of the longest substring.
// Row in this table represents the string_1 and the coloum as string_2.
// create a 2-D array named dp and intitialise all the values as zero.
int dp[2][N + 1];
// To store length of the longest
// common substring
int LCSCount = 0;
// Following steps to fill the values in the dp array in bottom-up manner
// Iterative approach for filling the values.
for (int i = 1; i <= M; i++){
// column iterates over the second string
for (int j = 1; j <= N; j++){
// Base Case
if (i == 0 || j == 0)
dp[i][j] = 0;
// if the characters at string_1 and string_2 matches
else if (string_1[i - 1] == string_2[j - 1]){
dp[i%2][j] = dp[(i - 1)%2][j - 1] + 1;
// carry forwarding the maximum element in the table
LCSCount = max(LCSCount, dp[i%2][j]);
}
else
// if the characters did not match then the values is zero
dp[i%2][j] = 0;
}
}
// return the maximum element in the dp table
return LCSCount;
}
// Driver code
int main(){
// Given two strings are
string string_1 = "acdefb";
string string_2 = "nbgacde";
// length of two strings
int M = string_1.length();
int N = string_2.length();
// call for the LCS function to get the length of the longest common substring
cout << LCS(string_1, string_2, M, N);
return 0;
}
Output:
4
Python implementation for finding the length of the longest substring by space optimizing using DP state:
# Python program for finding the length of the longest common substring using dynamic programming
def LCS(string_1, string_2, M, N):
# This table keeps track of the substrings which are common and contains the length of the longest substring.
# create a 2-D array named dp and intitialise all the values as zero.
dp = [[0 for k in range(N+1)] for l in range(2)]
# To store the length of longest common substring
LCSCount = 0
# Following steps to fill the values in the dp array in bottom-up manner
# Iterative approach for filling the values.
for i in range(1, M + 1):
# column iterates over the second string
for j in range(1, N + 1):
# Base Case
if (i == 0 or j == 0):
dp[i][j] = 0
# if the characters at string_1 and string_2 matches
elif (string_1[i-1] == string_2[j-1]):
dp[i%2][j] = dp[(i-1)%2][j-1] + 1
# carry forwarding the maximum element in the table
LCSCount = max(LCSCount, dp[i%2][j])
# if the characters did not match then the values is zero
else:
dp[i%2][j] = 0
# return the maximum element in the dp table
return LCSCount
# Driver code
if __name__ == "__main__":
# Given two strings are
string_1 = "acdefb"
string_2 = "nbgacde"
# length of two strings is
N = len(string_1)
M = len(string_2)
# Call the LCS function by passing the parameters
print(LCS(string_1, string_2, N, M))
Output:
4
Java implementation for finding the length of the longest substring by space optimizing using DP state:
// java program for finding the length of the longest common substring using dynamic programming by space optimization technique
class Main {
// function which returns the length of longest common substring
static int LCS(char string_1[], char string_2[], int M, int N) {
// This table keeps track of the substrings which are common
// and contains the length of the longest substring.
// Row in this table represents the string_1 and the coloum as string_2.
// create a 2-D array named dp and intitialise all the values as zero.
int dp[][] = new int[2][N + 1];
// To store length of the longest
// common substring
int LCSCount = 0;
// Following steps to fill the values in the dp array in bottom-up manner
// Iterative approach for filling the values.
for (int i = 1; i <= M; i++){
for (int j = 1; j <= N; j++){
// # Base Case
if (i == 0 || j == 0){
dp[i][j] = 0;
}
// if the characters at string_1 and string_2 matches
else if (string_1[i - 1] == string_2[j - 1]){
dp[i%2][j] = dp[(i - 1)%2][j - 1] + 1;
// carry forwarding the maximum element in the table
LCSCount = Integer.max(LCSCount, dp[i%2][j]);
}
else{
// if the characters did not match then the values is zero
dp[i%2][j] = 0;
}
}
}
// return the maximum element in the dp table
return LCSCount;
}
// Driver code
public static void main(String[] args){
int M,N;
// Given two strings are
String string_1 = "acdefb";
String string_2 = "nbgacde";
// length of two strings
M = string_1.length();
N = string_2.length();
// call for the LCS function to get the length of the longest common substring
System.out.println(LCS(string_1.toCharArray(),string_2.toCharArray(), M, N));
}
}
Output:
4
Explanation: The longest common substring from the string_1 and string_2 of lengths N=6 and M=7 respectively, is “sing” and it is of length 4. Therefore the output is 4.
Complexity Analysis:
Time Complexity: O(M*N) where M and N are the lengths of string_1 and string_2 respectively.
- For filling up the DP table (2-D array) in a bottom-up manner, it requires a time of O(N*M).
Space Complexity: O(min(M*N)) where M and N are the lengths of string_1 and string_2 respectively.
- DP table (2-D array) is of size [2][min(N,M)+ 1], so the space occupied is min(M*N)*2.
- So the overall space complexity is O(min(M*N)).
Conclusion:
- We have discussed various approaches for finding the length of the longest substring.
- The first approach is by generating all the substrings of the given two strings of length M and N and comparing their substrings. It takes a time complexity of O(N^2 * M^2), this can be optimized by comparing only the same length substrings and it takes the time complexity of O(N^3) where the length of both the strings is the same N.
- The second approach uses recursion for finding the length of the longest common substring this takes a time complexity of O(3^(N+M)) and space complexity of O(M+N)
- Whenever a recursive approach is present, and a recursive tree is formed we observe that dynamic programming can be used to overcome the re-calculation of the sub-problems again and again.
- Instead, we compute the results of all sub-problems and store them. They are extracted whenever required for solving the real problem.
- So in this way, we get the third approach which uses dynamic programming for finding the length of the longest common substring from the given two strings. We write DP state and store the values in a 2-D DP table. This takes the time complexity of O(N*M) and space complexity O(N*M) for the DP table.
- The fourth approach is the same DP approach but space optimization is done by, simply storing the previous row, therefore the time complexity remains the same i.e, O(N*M) and space complexity is O(2*min(M, N)).
HAPPY CODING!!!