Searching is a method to find some relevant information in a data set. In computer programming, searching is usually referred to as finding a particular element in a data structure. Linear search algorithm is a straightforward search algorithm. This type of search performs a sequential search on all items individually. In this article, we will be learning about Linear Search Algorithm.
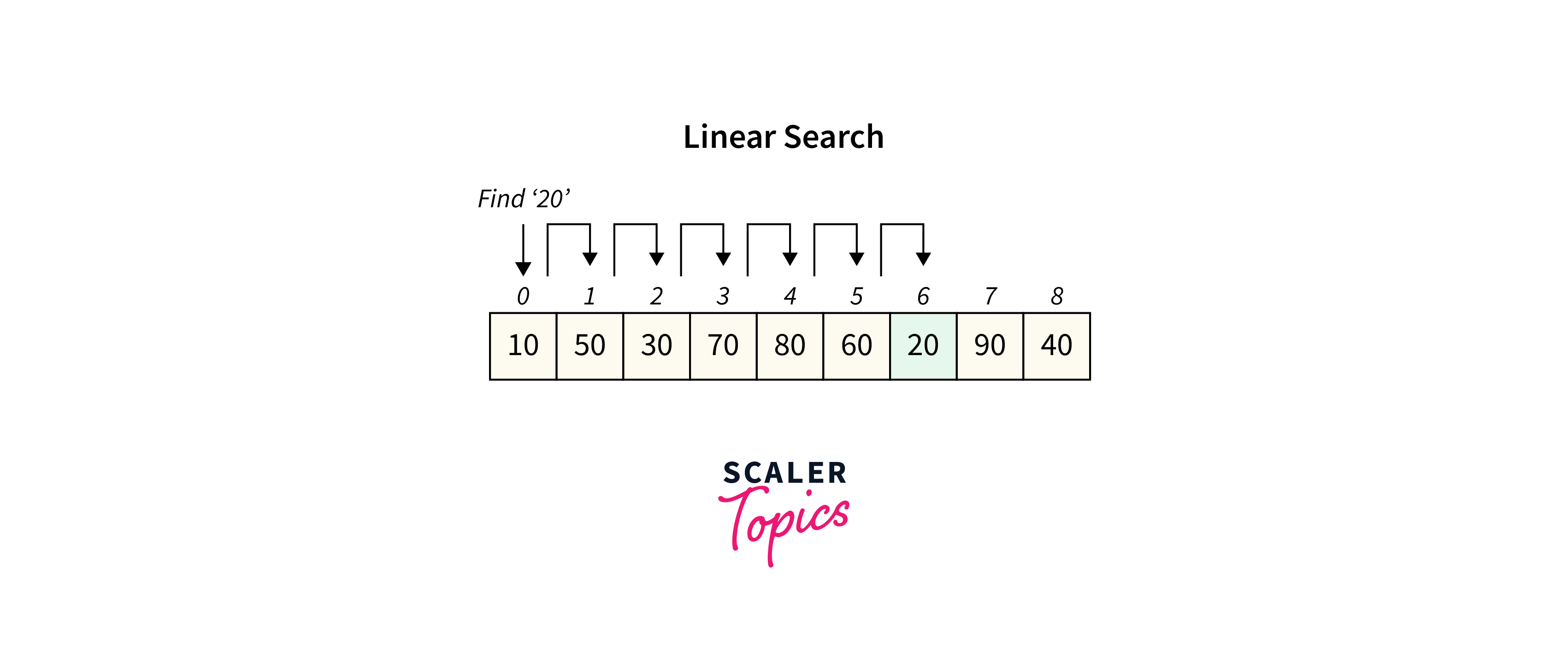
How Linear Search Algorithm Works?
Linear search is an algorithm which is used to find a target value within an array of elements. Here’s how it works:
- Start from the beginning of the array (i = 0) and traverse each element sequentially.
- If the current element equals the target value (arr[i] == K), return the index i.
- If the end of the array is reached without finding the target value (i >= n), return -1 to indicate that the value was not found.
- If the current element doesn’t match with the target value, move to the next element (i++) and repeat the process.
Linear Search Algorithm: Finding a Number in an Array
Linear search is a simple algorithm which is used to find a target value within an array of elements. Imagine you have an array of integers like this:
5 3 12 9 45 1 22
And you want to find the number 9 within this array.
- Start from the beginning of the array (i = 0) and traverse each element sequentially.
- If the current element equals the target value (arr[i] == 9), return the index i.
- If the end of the array is reached without finding the target value (i >= n), return -1 to indicate that the value was not found.
- If the current element does not match the target value, and then it will move to the next element (i++) and repeat the process.

Implementation of Linear Search Algorithm
Below is a Simple Implementation of Linear Search in Java.
public class ScalerTopics
{
public static void main(String[] args) {
int[] array = new int[] {5, 3, 12, 9, 45, 1, 22};
int K = 9;
int result = linearSearch(array, K);
if (result >= 0) {
System.out.println(K + " found at index: " + result);
} else {
System.out.println(K + " not found");
}
}
private static int linearSearch(int[] array, int K) {
int n = array.length;
for (int index = 0; index < n; ++index) {
if (array[index] == K) {
return index;
}
}
return -1;
}
}
Below is a Simple Implementation of Linear Search in Python.
def linear_search(array, K):
for index, value in enumerate(array):
if value == K:
return index
return -1
def main():
array = [5, 3, 12, 9, 45, 1, 22]
K = 9
result = linear_search(array, K)
if result >= 0:
print(f"{K} found at index: {result}")
else:
print(f"{K} not found")
if __name__ == "__main__":
main()
Below is a Simple Implementation of Linear Search in C++.
#include <iostream>
#include <vector>
int linearSearch(const std::vector<int>& array, int K) {
for (size_t index = 0; index < array.size(); ++index) {
if (array[index] == K) {
return index;
}
}
return -1;
}
int main() {
std::vector<int> array = {5, 3, 12, 9, 45, 1, 22};
int K = 9;
int result = linearSearch(array, K);
if (result >= 0) {
std::cout << K << " found at index: " << result << std::endl;
} else {
std::cout << K << " not found" << std::endl;
}
return 0;
}
Output
9 found at index: 3
Complexity Analysis of Liner Search Algorithm
Time Complexity of Linear Search Algorithm
Best case: In the best case, we might find K in the first iteration only, i.e. it is the first element of the array, so it is O(1).
Worst case: In the worst case, **we might find K in the last iteration or not find K in the array.
On average, it might be present around the middle of the array, so its complexity is O(n/2) ~ O(n).
Space Complexity of Linear Search Algorithm
As it is evident, we are not using any significant extra memory in linear search. So the space complexity is constant, i.e. O(1).
Advantage of Liner Search Algorithm
The advantages of the Linear Search Algorithm include:
- Simplicity: Linear search is straightforward to implement, making it suitable for beginners and for situations where simplicity is preferred over efficiency.
- Applicability to Unsorted Data: Unlike other search algorithms like binary search, which require sorting data, linear search can be applied to both sorted and unsorted arrays.
- No Preprocessing Required: Linear search requires no data preprocessing before searching, making it efficient for searching in dynamic or frequently changing data sets.
- Ease of Understanding: The algorithm is straightforward, making it accessible for those new to programming or algorithms.
Drawbacks of Liner Search Algorithm
The drawbacks of the Linear Search Algorithm include:
- For large data sets, linear search may need to be more efficient than other search algorithms with lower time complexities.
- Linear search traverses the entire array even if the target element is found early in the search process. This can result in unnecessary comparisons and wasted computational resources.
- The efficiency of linear search depends on the distribution of data. Linear search may need more comparisons on average if the target element is towards the end of the array rather than evenly distributed throughout it.
When to use Linear Search Algorithm?
Linear search in Data Structure is widely used, and these are the following scenarios:
- Linear search works fine when we will be using small data sets.
- Linear search within Data Structures finds everyday use within singly-linked lists.
- Linear search is used when frequent updates are needed.
Conclusion
- Linear search is a simple search-based algorithm that sequentially scans through all elements in a data collection to find a target element.
- In the worst and average cases, the time complexity of the Linear search algorithm is O(n).
- Advantages of linear search include simplicity, applicability to unsorted data, no preprocessing required, and ease of understanding.
- Drawbacks of linear search include inefficiency for large data sets, unnecessary comparisons, and dependence on data distribution.
Stay tuned for the articles on Binary Search and Interpolation Search.
Thanks for reading. May the code be with you 🙂