Problem Statement
We are given an integer array nums and an integer k. We have to return the kth smallest element in the array where $k <=$ size of nums. Also, note that we have to return the $kth$ smallest element not the kth distinct element.
Example
nums = {9,6,1,12,56,5,4,2,5}
k = 4Example Explanation
If we sort the above array, this will lead us to an array,
$1,2,4,5,5,6,9,12,56$
In the above-sorted array, the $1st$ smallest element is 1, the $2nd$ smallest element is 2, the $3rd$ smallest element is 4, the $4th$ smallest element is 5, the $5th$ smallest element is 5, …., the $9th$ smallest element is 56.
So the $4th$ smallest element is 5, hence the output of the program should be 5.
Constraints
If n is the number of elements in nums then,
$1 <= k <= n <= 10^4$
and if $nums[i]$ represents the $ith$ element of the nums array then,
$-10^4 <= nums[i] <= 10^4$
Approach – 1 : Brute Force, Using Sorting
We will consider the same example we used above,
nums = {9,6,1,12,56,5,4,2,5}
k = 4Then the sorted version of the above array will look like this,
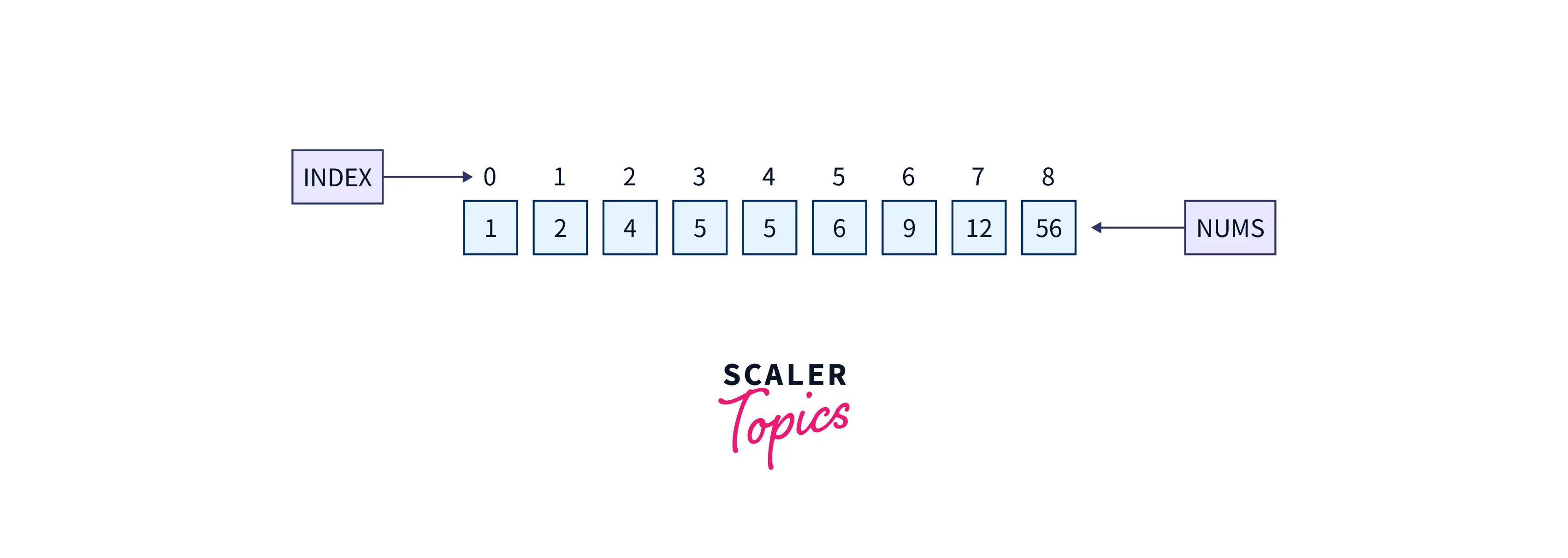
Notice here, the $0th$ index is having $1st$ smallest element $i.e$ 1,
the $1st$ index is having the $2nd$ smallest element $i.e$ 2,
the $2nd$ index is having the $3rd$ smallest element $i.e$ 4,
and so on.
So after sorting the array, the $kth$ smallest element is at $(k-1)th$ index.
Algorithm
- Sort the array in increasing order.
- Return the element present at $(k-1)th$ index as the array is $0-indexed$.
Code Implementation
C++ :
#include <algorithm>
#include <iostream>
using namespace std;
int main() {
//Initializing the nums, k, and n
int nums[] = {9,6,1,12,56,5,4,2,5};
int k = 4, n = sizeof(nums)/sizeof(nums[0]);
//Sorting the nums array
sort(nums,nums+n);
cout<<k<<"th smallest element is: "<<nums[k-1]<<endl;
return 0;
}Output :
4th smallest element is: 5Java :
import java.util.Arrays;
import java.util.Collections;
class Main {
public static void main(String args[]) {
//Initializing the nums, and k
Integer nums[] = new Integer[] {9,6,1,12,56,5,4,2,5};
int k = 4;
//Sorting the nums array
Arrays.sort(nums);
System.out.print(k+"th smallest element is: " + nums[k-1]);
}
}
Output :
4th smallest element is: 5
Python :
# Initializing the nums and k
nums = [9,6,1,12,56,5,4,2,5]
k = 4
# Sorting the nums array
nums.sort()
print(k,"th smallest element is:", nums[k-1])
Output :
4 th smallest element is: 5
Time Complexity
Since we are sorting the array, we can use Heap Sort and the worst time complexity for sorting the array is $O(NlogN)$, and then we are returning the $(k-1)th$ index in $O(1)$. Therefore time complexity of the above algorithm is, $O(NLogN)$.
Space Complexity
As we are using Heap Sort and Heap Sort doesn’t require any extra space, therefore the space complexity is, $O(1)$.
Approach – 2 : Using Set from C++ STL
If the elements of nums are distinct, then we can use sets to find the $kth$ smallest element as set in C++ STL stores the element in sorted order. As the elements are in sorted order, therefore we can use this property for finding the $kth$ smallest element. But there’s a constraint that the elements of nums should be distinct.
As we have to find the $kth$ smallest element, then we have to skip the first $(k-1)$ elements as the elements in the set are sorted. Like in the above example where the $1st$ smallest element is at 0.
Algorithm
- Insert all the elements of the nums into a set.
- Initialize an iterator to the beginning of the set.
- Advance the iterator to the $kth$ element by skipping the first $(k-1)$ elements as the elements are sorted.
Code Implementation
C++ :
#include <bits/stdc++.h>
using namespace std;
int main() {
//Initializing the nums, k, and n
int nums[] = {9,6,1,12,56,5,4,2,5};
int k = 4, n = sizeof(nums)/sizeof(nums[0]);
//Initializing the set and iterator
set<int> s(nums,nums+n);
auto itr = s.begin();
//Advancing the iterator to a kth element by skipping the first k-1 elements
advance(itr,k-1);
cout<<k<<"th smallest element is: "<<*itr<<endl;
return 0;
}
Output :
4th smallest element is: 5
Time Complexity
A Set in C++ STL takes $O(LogN)$ time for insertion in the worst case and we are inserting all the elements of nums to the set. Therefore the time complexity of this approach is $O(NLogN)$.
Space Complexity
Since we are using a set and storing the elements of the nums in the set, the space complexity is $O(N)$ for the extra set used.
Approach – 3 : Using Min-Heap
As we are interested in the smallest or minimum element, think of a data structure that can help us to get the smallest or minimum element in the best time. You guessed it right, it’s min-heap. Min heap stores elements in increasing order, hence the smallest element is at the top of the min-heap.
Now heaps itself is a vast topic and you can learn more about heaps here at Heap Data Structure.
For the time being, we will be assuming that you are familiar with the working of heaps and we will be using a priority queue.
Algorithm
- Build the min-heap by passing all the elements of nums to the min-heap. So the size of the min-heap will be equal to the size of
nums. - Pop $(k-1)$ elements from the min-heap.
- $Kth$ smallest element is at the top of the min-heap.
Code Implementation
C++ :
#include <bits/stdc++.h>
using namespace std;
int main() {
//Initializing the nums, k, and n
int nums[] = {9,6,1,12,56,5,4,2,5};
int k = 4, n = sizeof(nums)/sizeof(nums[0]);
//Building the min-heap using a priority queue
priority_queue<int, vector<int>, greater<int>> mhDS(nums, nums+n);
//Popping k-1 elements from the min-heap
for(int i=0;i<k-1;i++){
mhDS.pop();
}
cout<<k<<"th smallest element is: "<<mhDS.top()<<endl;
return 0;
}
Output :
4th smallest element is: 5
Java :
import java.util.Arrays;
import java.util.PriorityQueue;
class Main {
public static void main(String args[]) {
//Initializing the nums and k
Integer nums[] = new Integer[] {9,6,1,12,56,5,4,2,5};
int k = 4;
//Building the min-heap using a priority queue
PriorityQueue<Integer> mhDS = new PriorityQueue();
mhDS.addAll(Arrays.asList(nums));
//Popping k-1 elements from the min-heap
for (int i = 0; i < k - 1; i++) {
mhDS.poll();
}
System.out.print(k + "th smallest element is: " + mhDS.peek());
}
}
Output :
4th smallest element is: 5
Python :
import heapq
from heapq import heappop
# Initializing the nums and k
nums = [9,6,1,12,56,5,4,2,5]
k = 4
# Building the min-heap using priority queue
heapq.heapify(nums)
# Popping k-1 elements from the min-heap
for i in range(k - 1):
heappop(nums)
print(k,"th smallest element is:", nums[0])
Output :
4th smallest element is: 5
Time Complexity
An insertion in min-heap takes $O(LogN)$ in the worst case. We are inserting N elements in the min-heap. Therefore the time complexity of inserting N elements in a min-heap is $O(NLogN)$.
Also min-heap takes $O(1)$ to pop an element from the heap and we will be popping $(K-1)$ elements from the heap. So the overall time complexity of this approach is $O(NLogN + KLogN)$.
Space Complexity
Since we will be storing N elements in the min-heap, therefore the space complexity is $O(N)$ for the extra space used by Min-Heap.
Approach – 4 : Using Max-Heap
Max-heap has the property of storing max element at the top, so we can use this property. Instead of thinking of the problem like kth smallest element, think it of as the maximum element out of $k$ minimum elements. Like, consider the same array, here the $k$ minimum elements for $k=4$ are,
$1, 2, 4, 5$
Out of these elements, 5 is the maximum therefore 5 is our answer.
Let $k = 6$ then the k minimum elements are,
$1, 2, 4, 5, 5, 6$
Now our answer is 6.
We will store only k elements in the heap and will iterate over the remaining elements. If the current element is less than the top of the heap, it means we have to include this element in the heap. At the end of the iteration, we will be having a heap of k elements and the $kth$ smallest element is at the top of the heap.
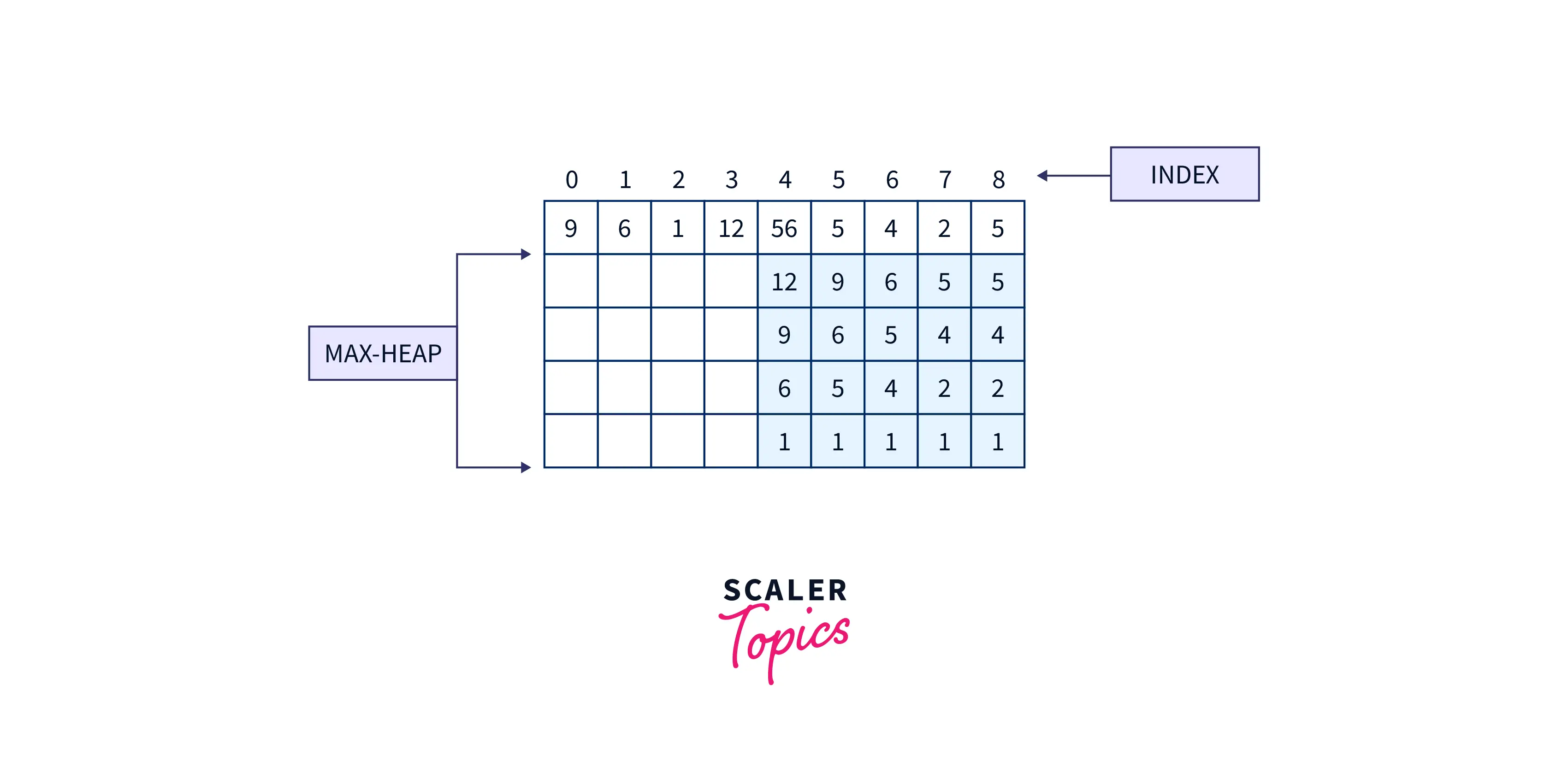
The above image demonstrates the state of the heap when we start at the ith index. For the $4th$ index, the top element of the heap is 12, and 56 was the current element. Since $56>12$, we skipped this element. At $i=5$ the current element is 5 and $5<12$, therefore we popped 12 and pushed 5 into the max-heap.
Algorithm
- Push first
kelements into the max-heap. - Iterate over the remaining elements of nums. If the current element $<$ top of the heap, pop the top element from the heap and push the current element into nums. So at any time, there will be only
kelements in the max-heap. - $Kth$ smallest element is at the top of the heap.
Code Implementation
C++ :
#include <bits/stdc++.h>
using namespace std;
int main() {
//Initializing the nums, k, and n
int nums[] = {9,6,1,12,56,5,4,2,5};
int k = 4, n = sizeof(nums)/sizeof(nums[0]);
//Building the max-heap
priority_queue<int, vector<int>> mhDS(nums, nums+k);
//Iterating over remaining elements of nums
for(int i=k;i<n;i++){
if(nums[i]<mhDS.top()){
//pop the top and push nums[i] to the max-heap
mhDS.pop();
mhDS.push(nums[i]);
}
}
cout<<k<<"th smallest element is: "<<mhDS.top()<<endl;
return 0;
}
Output :
4th smallest element is: 5
Java :
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Comparator;
class Main {
public static void main(String args[]) {
//Initializing the nums, k, and n
Integer nums[] = new Integer[] {9,6,1,12,56,5,4,2,5};
int k = 4;
int n = nums.length;
//Building the max-heap
PriorityQueue<Integer> mhDS = new PriorityQueue(Comparator.reverseOrder());
mhDS.addAll(Arrays.asList(nums));
//Iterating over remaining elements of nums
for(int i=k;i<n;i++){
if(nums[i]<mhDS.peek()){
//pop the top and push nums[i] to the max-heap
mhDS.poll();
mhDS.add(nums[i]);
}
}
System.out.print(k + "th smallest element is: " + mhDS.peek());
}
}
Output :
4th smallest element is: 5
Python :
import heapq
# Implementation of Max-Heap based on heapq
class MaxHeap:
def __init__(self, data=None):
if data is None:
self.data = []
else:
self.data = [-i for i in data]
heapq.heapify(self.data)
def top(self):
return -self.data[0]
def push(self, item):
heapq.heappush(self.data, -item)
def pop(self):
return -heapq.heappop(self.data)
def replace(self, item):
return heapq.heapreplace(self.data, -item)
# Initializing the nums and k
nums = [9,6,1,12,56,5,4,2,5]
k = 4
n = len(nums)
# Building the max-heap
mhDS = MaxHeap(nums[0:k])
# Iterating over remaining elements of nums
for i in range(k,n):
if nums[i]<mhDS.top():
# pop the top and push nums[i] to max-heap
mhDS.replace(nums[i])
print(k,"th smallest element is:", mhDS.top())
Output :
4 th smallest element is: 5
Time Complexity
As we build the heap with K elements, and then iterate over $N-K$ elements and push them to the max-heap. Therefore the time complexity is $O(K + (N-K)LogK)$. $O(K)$ for building the max-heap of K elements and for the remaining $(N-K)$ elements it can take upto $O(LogK)$for the insertion of each element in the max-heap. So overall time complexity is $O(K + (N-K)LogK)$.
Space Complexity
At any instant, we will be storing k elements in the heap, therefore space complexity is $O(K)$.
Approach – 5 : Using Quick Select
As the name implies Quick Select is similar to Quick Sort. Quick Sort selects a pivot element, moves it to the right location, and partitions the surrounding array such that the elements smaller than the pivot are on the left side, and elements greater than the pivot are on the right side. But unlike quick sort where we process both sides of the array, here we will only process one side of the array.
We process either the left side of the pivot element or the right side of the pivot as we are only interested in the case where the pivot is our kth smallest element. When the pivot is our $kth$ smallest element, the index of pivot will be $(k-1)$ as we checked above in the case of sorting. When we finish the processing for pivot or $kth$ smallest element, it means there are $(k-1)$ elements smaller than the pivot hence our $kth$ smallest element is the pivot.
Algorithm
Considering l is the lower index of the array and h is a higher index of the array :
- Partition the array around the pivot and return the index of the pivot.
- If index of pivot : $l == k-1$ then the $kth$ smallest element is at index of pivot as there are $(k-1)$ elements lesser than the pivot.
- If index of pivot : $l > k-1$, then we should process the left side as the index of pivot is greater.
- Else we should process the right side of the array as the index of pivot is smaller.
Code Implementation
C++ :
#include <bits/stdc++.h>
using namespace std;
//Partition the nums and return the index of pivot
int partition(int nums[], int l, int h)
{
int x = nums[h], i = l;
for (int j = l; j <= h - 1; j++) {
//Swapping smaller elements to the left side of the pivot
if (nums[j] <= x) {
swap(nums[i], nums[j]);
i++;
}
}
swap(nums[i], nums[h]);
return i;
}
int kthSmallest(int nums[], int l, int h, int k)
{
if (k > 0 && k <= h - l + 1) {
// Partition the nums array and get the index of the pivot
int index_of_pivot = partition(nums, l, h);
if (index_of_pivot - l == k - 1) //Kth smallest element is at index_of_pivot
return nums[index_of_pivot];
if (index_of_pivot - l > k - 1) // Process the left side
return kthSmallest(nums, l, index_of_pivot - 1, k);
// Else Process right side
return kthSmallest(nums, index_of_pivot + 1, h, k - index_of_pivot + l - 1);
}
// If k is not in the range of nums
return INT_MAX;
}
int main() {
//Initializing the nums, k, and n
int nums[] = {9,6,1,12,56,5,4,2,5};
int k = 4, n = sizeof(nums)/sizeof(nums[0]);
int ans = kthSmallest(nums,0,n-1,k);
cout<<k<<"th smallest element is: "<<ans<<endl;
return 0;
}
Output :
4th smallest element is: 5
Java :
import java.util.Arrays;
import java.util.Collections;
class Main {
public static int partition(Integer[] nums, int l,int h)
{
int x = nums[h], i = l;
for (int j = l; j <= h - 1; j++) {
if (nums[j] <= x) {
//Swapping smaller elements to the left side of the pivot
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
i++;
}
}
// Swapping
int temp = nums[i];
nums[i] = nums[h];
nums[h] = temp;
return i;
}
public static int kthSmallest(Integer[] nums, int l, int h, int k)
{
if (k > 0 && k <= h - l + 1) {
// Partition the nums array and get the index of the pivot
int index_of_pivot = partition(nums, l, h);
if (index_of_pivot - l == k - 1) //Kth smallest element is at index_of_pivot
return nums[index_of_pivot];
if (index_of_pivot - l > k - 1) // Process the left side
return kthSmallest(nums, l, index_of_pivot - 1, k);
// Else Process right side
return kthSmallest(nums, index_of_pivot + 1, h, k - index_of_pivot + l - 1);
}
// If k is not in the range of nums
return Integer.MAX_VALUE;
}
public static void main(String args[]) {
//Initializing the nums, k, and n
Integer nums[] = new Integer[] {9,6,1,12,56,5,4,2,5};
int k = 4;
int n = nums.length;
int ans = kthSmallest(nums,0,n-1,k);
System.out.print(k + "th smallest element is: " + ans);
}
}
Output :
4th smallest element is: 5
Python :
import sys
# Partition the nums and return the index of pivot
def partition(nums, l, h):
x = nums[h]
i = l
for j in range(l, h):
# Swapping smaller elements to the left side of the pivot
if (nums[j] <= x):
nums[i], nums[j] = nums[j], nums[i]
i += 1
nums[i], nums[h] = nums[h], nums[i]
return i
def kthSmallest(nums, l, h, k):
if (k > 0 and k <= h - l + 1):
# Partition the nums array and get the index of pivot
index_of_pivot = partition(nums, l, h)
if (index_of_pivot - l == k - 1): #Kth smallest element is at index_of_pivot
return nums[index_of_pivot]
if (index_of_pivot - l > k - 1): # Process the left side
return kthSmallest(nums, l, index_of_pivot - 1, k)
# Else Process right side
return kthSmallest(nums, index_of_pivot + 1, h,k - index_of_pivot + l - 1)
return sys.maxsize
# Initializing the nums, k, and n
nums = [9,6,1,12,56,5,4,2,5]
k = 4
n = len(nums)
print(k,"th smallest element is:", kthSmallest(nums, 0, n - 1, k))
Output :
4 th smallest element is: 5The average case time complexity is $O(N)$ and the worst-case time complexity is $O(N^2)$ when the elements of $nums$ are in decreasing order and we choose the rightmost element as the pivot.
Space Complexity
Since we are using recursion and in each step of the recursion we either proceed with the left side or right side of the array. Therefore with each step, our problem is reduced by half. Hence the space complexity is $O(LogN)$ for the recursion stack space.
Approach – 6 : Using Binary Search
If we look at approach 1, we can notice that the $k^{th}$ smallest element is at the $k-1^{th}$ index. Let $x$ be the $k^{th}$ smallest element, so there will be at least k elements (including $x$) that are less than or equal to x. We will use binary search to predict the element’s position in a sorted array without actually sorting the array.
Consider the array,
$9,6,1,12,56,5,4,2,5$
and
$k = 4$
We have to find an element that has k elements (including self) lesser to it. In the above case for element 5, there are 3 elements lesser than 5 and these are $4,2,1$ if we include 5 this will lead us to k. Therefore 5 is the $kth$ smallest element.
Let’s understand how we will proceed with binary search in this problem, We will iterate over $[$min of nums, max of nums$]$ and for each mid in the range we will check whether the number of elements less than or equal to mid is k or not.
If the mid’s count $< k$, it means that we need to increase mid so that count can also increase.
In the other case if mid’s count $> k$, we need to decrease the mid so that the count can also decrease.
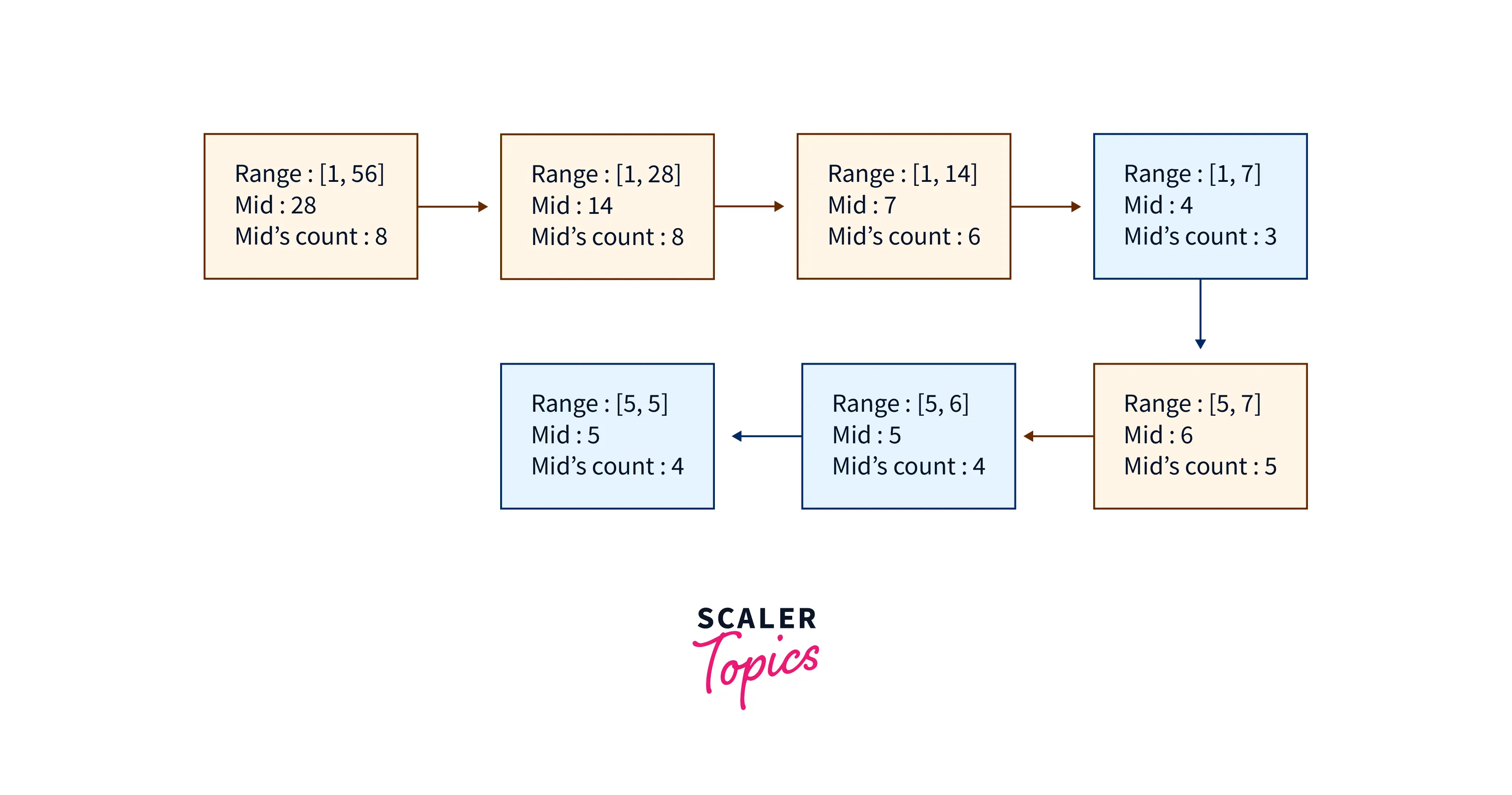
The yellow block contains the cases where mid’s count $> k$, here 4. And the blue contains the case where mid’s count $<= k$.
Algorithm
Considering $l$ is the minimum element of the array and $h$ is a maximum element of the array :
- Perform the following operation while $l<h$,
- Calculate mid by $l+(h-l)/2$.
- Check if mid can be the kth smallest element by counting the that have value less than or equal to mid.
- If $count$ $< k$ then set $l = mid+1$ as the count is less than
kand we need to increase the mid so the count can be equal tok, else set $h = mid$, so that count can be decremented tok. - At the end of the while loop,
lwill be storing the $kth$ smallest element of the array.
Code Implementation
C++ :
#include <bits/stdc++.h>
using namespace std;
int count(int nums[], int n, int mid){
int cnt = 0;
// If an element of the array <= mid increase the count var by 1
for(int i = 0; i < n; i++) if(nums[i] <= mid) cnt++;
return cnt;
}
int main() {
//Initializing the nums, k, and n
int nums[] = {9,6,1,12,56,5,4,2,5};
int k = 4, n = sizeof(nums)/sizeof(nums[0]);
int l = INT_MAX, h = INT_MIN,mid,cnt;
//Calculating minimum and maximum elements in nums
for(int i=0;i<n;i++){
l = min(l,nums[i]);
h = max(h,nums[i]);
}
while(l<h){
mid = l+(h-l)/2;
//Counting the elements less than or equal to mid
cnt = count(nums,n,mid);
if(cnt<k) l = mid+1;
else h = mid;
}
cout<<k<<"th smallest element is: "<<l<<endl;
return 0;
}
Output :
4th smallest element is: 5
Java :
import java.util.Arrays;
import java.util.Collections;
class Main {
static int count(Integer nums[], int n, int mid){
int cnt = 0;
// If an element of the array <= mid increase the count var by 1
for(int i = 0; i < n; i++) if(nums[i] <= mid) cnt++;
return cnt;
}
public static void main(String args[]) {
//Initializing the nums, k, and n
Integer nums[] = new Integer[] {9,6,1,12,56,5,4,2,5};
int k = 4, n = nums.length;
int l = Integer.MAX_VALUE, h = Integer.MIN_VALUE,mid,cnt;
//Calculating minimum and maximum elements in nums
for(int i=0;i<n;i++){
l = Math.min(l,nums[i]);
h = Math.max(h,nums[i]);
}
while(l<h){
mid = l+(h-l)/2;
//Counting the elements less than or equal to mid
cnt = count(nums,n,mid);
if(cnt<k) l = mid+1;
else h = mid;
}
System.out.print(k + "th smallest element is: " + l);
}
}
Output :
4th smallest element is: 5
Python :
import sys
def count(nums, mid):
cnt = 0
# If an element of the array <= mid increase the count var by 1
for i in range(len(nums)):
if nums[i] <= mid:
cnt += 1
return cnt
# Initializing the nums and k
nums = [9,6,1,12,56,5,4,2,5]
k = 4
l = sys.maxsize
h = -sys.maxsize - 1
# Calculating minimum and maximum elements in nums
for i in range(len(nums)):
l = min(l, nums[i])
h = max(h, nums[i])
while l < h:
mid = l + (h - l) // 2
# Counting the elements less than or equal to mid
if count(nums, mid) < k:
l = mid + 1
else:
h = mid
print(k,"th smallest element is:", l)
Output :
4 th smallest element is: 5
Time Complexity
If $l$ is the minimum element and h is the maximum element of the array, then the time complexity is $O(N*Log(h-l))$ as we are performing binary search over the range $[l, h]$ and each iteration costs $O(N)$ for count function.
Space Complexity
Since we are not using any other data structure except the nums array, the space complexity is $O(1)$.
Approach – 7 : Using Map
If we create a map of elements of the nums with their frequencies, and as the map stores data in an ordered way. Therefore we can iterate over the frequencies of the elements and if, at any instant sum of frequencies $>= k$, the $kth$ smallest element will be the key to the current mapping.
Consider the array,
$9,6,1,12,56,5,4,2,5$
and
$k = 4$
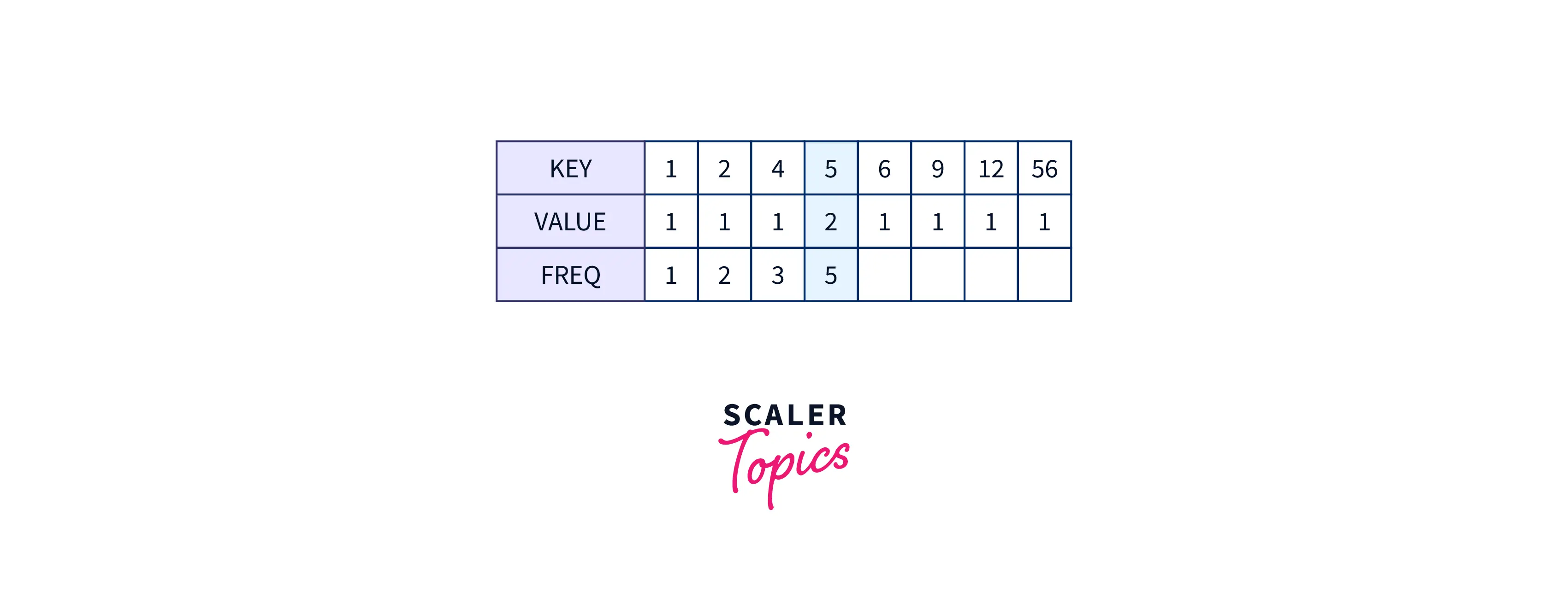
In the above image we can see that for key $= 5$, we have freq $= 5$ which is greater than k. Therefore 5 is the $kth$ smallest element.
Algorithm
- Map all the elements of the nums with their frequencies.
- Declare a freq $= 0$ variable and iterate over the mapping in the map, for each mapping add the frequency to freq.
- If freq$>=k$, the kth smallest element is the key to the current mapping and breaks the loop.
Code Implementation
C++ :
#include <bits/stdc++.h>
using namespace std;
int main() {
//Initializing the nums, k, and n
int nums[] = {9,6,1,12,56,5,4,2,5};
int k = 4, n = sizeof(nums)/sizeof(nums[0]);
//Building the map by mapping the element with its frequency
map<int,int> mp;
for(int i=0;i<n;i++){
mp[nums[i]]++;
}
int freq = 0, ans = -1;
// Iterating over the map to calculate the frequency
for(auto x:mp){
freq+=x.second;
if(freq>=k){
ans = x.first;
break;
}
}
cout<<k<<"th smallest element is: "<<ans<<endl;
return 0;
}
Output :
4th smallest element is: 5
Java :
import java.util.*;
class Main {
public static void main(String args[]) {
//Initializing the nums, k, and n
Integer nums[] = new Integer[] {9,6,1,12,56,5,4,2,5};
int k = 4, n = nums.length;
//Building the map by mapping the element with its frequency
TreeMap<Integer, Integer> mp = new TreeMap<>();
for(int i=0;i<n;i++){
mp.put(nums[i], mp.getOrDefault(nums[i], 0) + 1);
}
int freq = 0, ans = -1;
// Iterating over the map to calculate the frequency
for (Map.Entry it : mp.entrySet())
{
freq += (int)it.getValue();
if (freq >= k) {
ans = (int)it.getKey();
break;
}
}
System.out.print(k + "th smallest element is: " + ans);
}
}
Output :
4th smallest element is: 5Time Complexity
Since we are interested in the sorted order of the elements in the map, we are using map in C++ and TreeMap in Java. Both these maps take $O(LogN)$ time for inserting an element. Therefore for N elements the time complexity is $O(NLogN)$. Then we iterate over K values in the map, therefore overall time complexity of this approach is $O(NLogN + K)$
Space Complexity
As we are storing N elements in the map, therefore the space complexity is $O(N)$.
Conclusion
- In the $kth$ smallest element we are given an array and we have to find the $kth$ smallest element in the array.
- It is to note that we are talking about $kth$ smallest element not about $kth$ distinct element in the array.
- There are multiple ways to solve this problem such as Sorting, Set from C++ STL, Min-Heap, Max-Heap, Quick Select, Binary Search, and Map.