Problem Statement
We are provided with a Binary Search tree and the task is to find the $k^{th}$ largest element in BST (Binary Search Tree).
Refer to the Example and Example Explanation sections for more details and the Approach section to understand how to find the $k^{th}$ largest element in bst.
Example
Example 1:
The given input binary search tree is:
10
/ \
4 20
/ / \
2 15 40The value of k is: 3
So, the $3^{rd}$ largest element comes out to be: 15.
Example 2:
The given input binary search tree is:
27
/ \
25 30
/ \ \
22 26 34The value of k is: 2
So, the $2^{nd}$ largest element comes out to be: 30.
Example Explanation
Before getting into the explanation of the example and how to $k^{th}$ largest element in bst, let us first get a brief introduction about the binary search tree.
A binary search tree can be defined as a collection of objects or elements or entities known as nodes. These nodes are linked together to represent a hierarchy. The top node of the hierarchy is known as the root node. Each node of a binary search tree contains some data and it can have at most two child nodes. A root node can never have a parent node. The nodes that do not have any child nodes are termed leaf nodes.
The main property of a binary search tree is that the left child of a node must be less than the current node and the right child of a node must be greater than the current node.
Example:
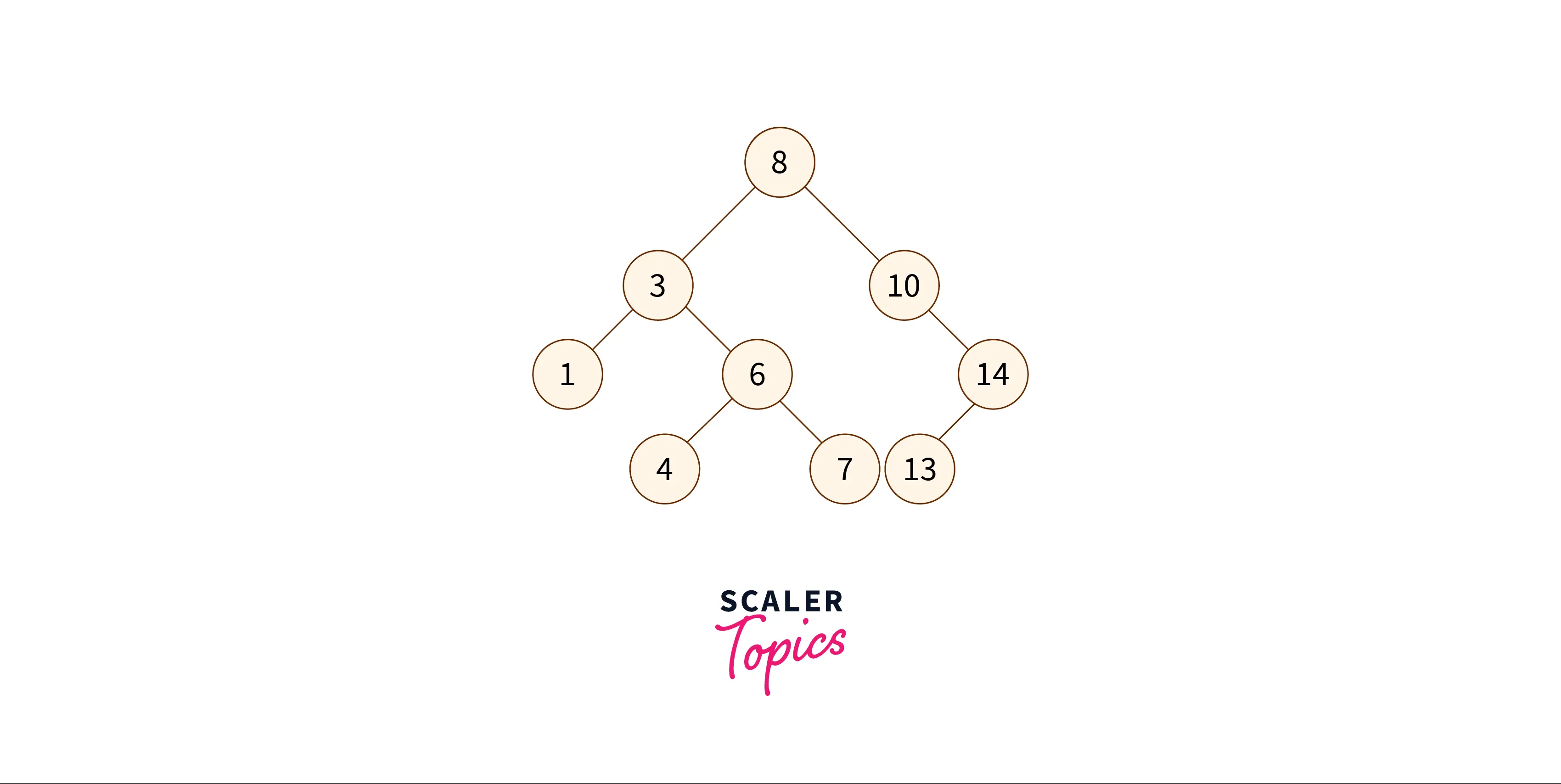
Let us take the first example provided above, the given binary search tree is:
10
/ \
4 20
/ / \
2 15 40In the binary search tree mentioned above, we can see that 40 is the first largest element, 20 is the second largest element and 15 is the third ($k^{th}$) largest element of the bst.
Since the right subtree contains the larger elements, we must look at the right subtree first.
Refer to the Approach section, for more clarity and to understand the other approaches to find the $k^{th}$ largest element in bst.
Input/Output
- The first input is the root node of the binary search tree
- The second input is the value of
k. - The third input is the value of
n, i.e. the number of nodes present in the bst.
Example:
The given input binary search is:
10
/ \
4 20
/ / \
2 15 40The given value of k is: 3
The given value of n is: 6
The output is:
The 3rd largest element of the binary search tree is: 15Constraints
1<= Number of nodes (n) <= $10^5$1<= Data of a node <= $10^5$
In some problems, you may find the number of test cases represented by t. So, we only need to call the findKthLargest() function t-times.
Approach 1: Naive Approach – Brute Force – using In-Order Traversal and Extra Space
The most basic approach to the problem – find the $k^{th}$ largest element in bst, we are going to traverse the entire binary search tree using the in-order traversal algorithm and side by side storing the values inside a data structure like an array or a list. Now, as we know that when we perform the in-order traversal of a binary search tree, we will get the nodes in ascending order (or increasing order) only.
So, we can perform the in-order traversal and keep on inserting the values into an array of sizes equal to the number of nodes of the binary search tree. Once the traversal is completed, we can simply return back the $n – k$ th index element from the array as the $k^{th}$ largest element in bst.
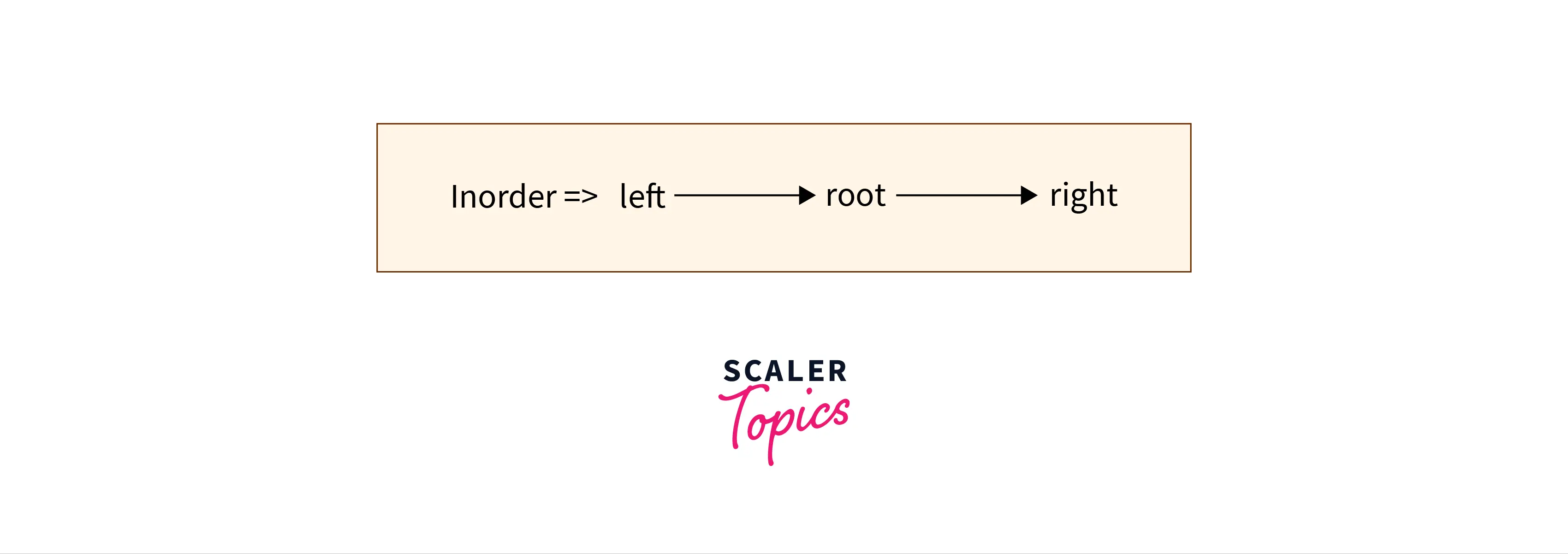
Before getting into the pseudo code and implementation, we should be familiar with the concept of in-order traversal. So, let us briefly discuss the in-order traversal of a binary search tree.
In the in-order tree traversal we first traverse the left subtree, then the root node, and finally the right subtree.
The pseudo-code for the in-order traversal can be:
- If the current node has a left child, recursively visit the left subtree (until NULL is found).
- Visit the root node.
- If the current node has the right child, recursively visit the right subtree (until NULL is found).
Let us take an example tree to understand and visualize the in-order traversal better.
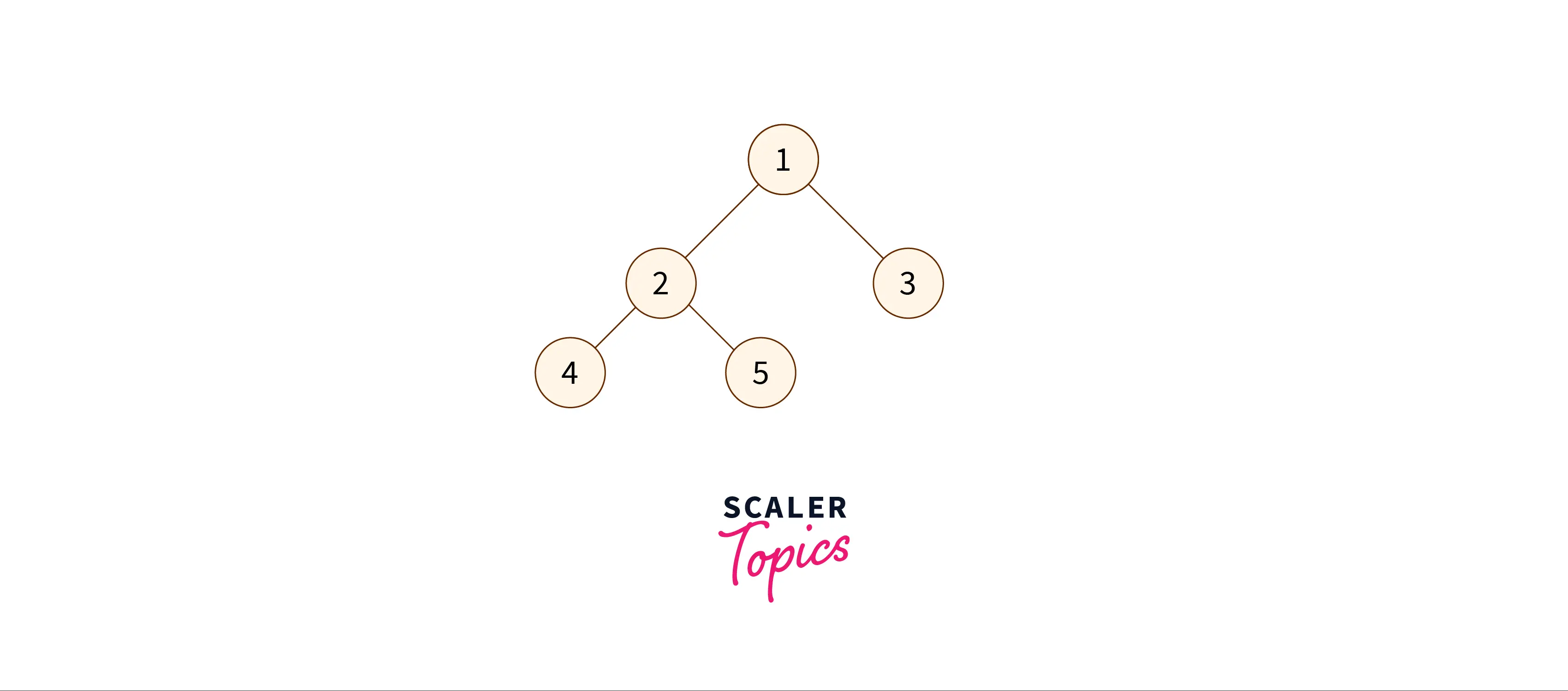
The final in-order traversal obtained will be: 4 2 5 1 3.
Algorithm
The pseudo-code for the above-discussed algorithm can be:
- Initialize an array of size =
ni.e. the number of nodes present in the binary search tree. - Start the in-order traversal of the binary search tree whose algorithm is discussed above. Now, in place of printing the current node’s data, we will insert the current node’s data into the array.
- At last return the $a[n-k]$ element as the $k^{th}$ largest element in bst.
Code Implementation
Let us code the above-discussed algorithm for better understanding.
C++ code:
// a function that will perform the in-order traversal of the bst
void inOrder(Node *root, int a[], int i) {
// checking the base case
if (root == NULL)
return;
// traversing the left subtree
inOrder(root->left, a, i);
// inserting the current root's data into the array
a[i++] = root->data;
// traversing the right subtree
inOrder(root->right, a, i);
}
// defining a function that will return the Kth largest element in bst.
int KthLargestElement(Node *root, int k, int n) {
// checking the base case
if (root == NULL)
return -1;
// initializing an array to store the elements of the bst.
int a[n];
// calling the helper in-order function
inOrder(root, a, 0);
// defining a counter and i which will help us to traverse the array.
int counter = 0;
int i = 0;
// decrementing the counter
while (counter < k) {
i = i - 1;
counter = counter + 1;
}
// returning the kth largest element of the bst
return a[i];
}Java code:
// a function that will perform the in-order traversal of the bst
static void inOrder(Node root, int a[], int i) {
// checking the base case
if (root == null)
return;
// traversing the left subtree
inOrder(root.left, a, i);
// inserting the current root's data into the array
a[i++] = root.data;
// traversing the right subtree
inOrder(root.right, a, i);
}
// defining a function that will return the Kth largest element in bst.
static int KthLargestElement(Node root, int k, int n) {
// checking the base case
if (root == null)
return -1;
// initializing an array to store the elements of the bst.
int a[] = new int[n];
// calling the helper in-order function
inOrder(root, a, 0);
// defining a counter and i which will help us to traverse the array.
int counter = 0;
int i = 0;
// decrementing the counter
while (counter < k) {
i = i - 1;
counter = counter + 1;
}
// returning the kth largest element of the bst
return a[i];
}Python code:
# a function that will perform the in-order traversal of the bst
def inOrder(root, a, i):
# checking the base case
if root is None:
return
# traversing the left subtree
inOrder(root.left, a, i)
# inserting the current root's data into the array
a[i] = root.data
i += 1
# traversing the right subtree
inOrder(root.right, a, i)
# defining a function that will return the Kth largest element in bst.
def KthLargestElement(root, k, n):
# checking the base case
if root is None:
return -1
# initializing an array to store the elements of the bst.
a = [0]*n
# calling the helper in-order function
inOrder(root, a, 0)
# defining a counter and i which will help us to traverse the array.
counter = 0
i = 0
# decrementing the counter
while (counter < k):
i = i - 1
counter = counter + 1
# returning the kth largest element of the bst
return a[i]When the Input tree is:
10
/ \
4 20
/ / \
2 15 40And the given value of k is: 3
Output
The kth largest element of the binary search tree is: 15In the brute force or basic approach to the problem – find the kth largest element in bst, we are traversing the input binary search tree only once using the in-order traversal of the binary search tree. We are using an extra array to store the node’s data.
Time Complexity
Since we are traversing the input binary search tree only once, the time complexity of the brute force approach to the problem – find the kth largest element in bst comes out to be O(n), where n is the size of the input binary search tree.
Space Complexity
Since we are using an extra array to store the node’s data, the space complexity of the brute force approach to the problem – find the kth largest element in bst comes out to be O(n), where n is the size of the array (same as the number of nodes of the bst).
Approach 2: Recursive Approach – using Reverse In-Order Traversal
Now as we have seen that we can use the in-order traversal and an array to find the kth largest element in bast, can we get our required answer without using the extra array? The answer is yes.
An efficient algorithm for the problem – to find the $k^{th}$ largest element in bst is to traverse the binary search tree in the reverse order using the in-order traversal. As we know that the in-order traversal of a binary search tree produces elements in increasing order. So, if we perform the reverse in-order traversal, we will get the elements in decreasing order.
Now, as we are performing the reverse in-order traversal, we need to keep track of several elements encountered which can easily be performed using a counter. So, when the counter reaches k we have found our kth largest element.
The reverse in-order traversal is simply traversing the right subtree then the root and finally the left subtree.
Algorithm
The pseudo-code for the above-discussed algorithm can be:
- Initialize a counter variable that will count the number of elements encountered in the binary search tree.
- Start the reverse in-order traversal of the binary search tree whose algorithm is discussed above. Now, in place of printing the current node’s data, we will decrement the counter.
- Before the left subtree call, we will check if the counter’s value has reached
kor not. If the counter’s value is the same askthen we will return the value of the node’s data. If the value ofcounteris less thankthen we will continue the above-stated process.
Code Implementation
Let us code the above-discussed algorithm for better understanding.
C++ code:
// defining a helper function that will return the Kth largest element in bst.
int helper(Node* root, int k, int &counter) {
// checking the base case
if (root == NULL || counter >= k)
return -1;
// calling the helper function for the right subtree.
helper(root->right, k , counter);
// incrementing the counter.
counter = counter + 1;
// checking if the counter's value is the same as k.
if (counter == k)
return root->data;
// calling the helper function for the left subtree.
helper(root->left, k , counter);
}
// defining a function that will call the helper function by providing the value of the counter
int KthLargestElement(Node* root, int k, int n) {
// checking the base case
if (root == NULL)
return -1;
int counter = 0;
int answer = helper(root, k, counter);
return answer;
}Java code:
// defining a helper function that will return the Kth largest element in bst.
static int helper(Node root, int k, int counter) {
// checking the base case
if (root == null || counter >= k)
return -1;
// calling the helper function for the right subtree.
helper(root.right, k , counter);
// incrementing the counter.
counter = counter + 1;
// checking if the counter's value is the same as k.
if (counter == k)
return root.data;
// calling the helper function for the left subtree.
helper(root.left, k , counter);
}
// defining a function that will call the helper function by providing the value of the counter
static int KthLargestElement(Node root, int k, int n) {
// checking the base case
if (root == null)
return -1;
int counter = 0;
int answer = helper(root, k, counter);
return answer;
}Python code:
# defining a function that will return the Kth largest element in bst.
def helper(root, k, counter):
# checking the base case
if root is None or counter >= k:
return -1
# calling the helper function for the right subtree.
helper(root.right, k, counter)
# incrementing the counter.
counter = counter + 1
# checking if the counter's value is the same as k.
if counter == k:
return root.data
# calling the helper function for the left subtree.
helper(root.left, k, counter)
# defining a function that will call the helper function by providing the value of the counter
def KthLargestElement(root, k, n):
# checking the base case
if root is None:
return -1
counter = 0
answer = helper(root, k, counter)
return answerWhen the Input tree is:
10
/ \
4 20
/ / \
2 15 40And the given value of k is: 3
Output
The kth largest element of the binary search tree is: 15In the recursive revere in-order traversal approach to the problem – find the $k^{th}$ largest element in bst, we are traversing the input binary search tree only once using the in-order traversal of the binary search tree. We are not using any extra space.
Time Complexity
Since we are traversing the input binary search tree only once, the time complexity of the recursive revere in-order traversal approach to the problem – find the kth largest element in bst comes out to be O(n), where n is the size of the input binary search tree.
Space Complexity
Since we are not using any extra space, the space complexity of the recursive revere in-order traversal approach to the problem – find the $k^{th}$ largest element in bst comes out to be O(1).
Note: There is O(h) space used for the recursion call stack, where h is the height of the binary search tree.
Approach 3: Iterative Approach – Reverse In-Order Traversal using Stack
So far we have seen two approaches that were based on recursion as we were using recursive in-order traversal approaches. Is there any way to solve the provided problem without using recursion? The answer is yes.
Another efficient algorithm for the problem – of finding the $k^{th}$ largest element in bst is to iteratively traverse the binary search tree in reverse order and store the values into a stack data structure (similar to what we have performed above in the reverse in-order traversal approach).
Note:
Stack in a linear data structure that stores data sequentially based on the Last In First Out (LIFO) manner. So, the data which is inserted first will be removed last.
As the stack supports last in first out, the element from the top to bottom of the stack must be containing the nodes of the binary search tree in decreasing order. So, after the traversal is completed, we can pop out the first k-1 elements from the stack. Now, the kth pooped element must be our required $k^{th}$ largest element of bst.
We can also decrement the counter (here k) whenever a new node is discovered. So when the value fo k becomes 0, we have found our required answer. Refer to the algorithm subsection for better clarity.
Algorithm
The pseudo-code for the above-discussed algorithm can be:
- Initialize a stack data structure.
- Insert the current node into the stack.
- Perform the following steps until the stack is not empty or we have entirely traversed the binary search tree.
- If the current node is not NULL (or None), insert the current node and move to the right subtree.
- Else, we will pop the top node from the stack and decrement the value of
k.- We will if the value of
khas become0ornot. If the value ofkis0then we would return the current node’s data as the $k^{th}$ largest element of bst. - Else, we would move to the left subtree of the current node.
- We will if the value of
Code Implementation
Let us code the above-discussed algorithm for better understanding.
C++ code:
// defining a function that will return the Kth largest element in bst.
int KthLargestElement(Node* root, int k, int n) {
// checking the base case
if (root == NULL)
return -1;
// defining a stack
stack <Node*> s;
// declaring a current pointer
Node* currentNode = root;
// traverse until the stack is not empty
while(!s.empty() || currentNode != NULL) {
// if the currentNode is not null, push it into the stack
if(currentNode != NULL) {
s.push(currentNode);
// moving to the right subtree
currentNode = currentNode->right;
}
else {
// getting the top element of the stack
currentNode = s.top();
s.pop();
// decrementing the value of k
k = k - 1;
if (k == 0) {
return currentNode->data;
}
// moving to the left subtree
currentNode = currentNode->left;
}
}
}Java code:
// defining a function that will return the Kth largest element in bst.
static int KthLargestElement(Node root, int k, int n) {
// checking the base case
if (root == null)
return -1;
// defining a stack
Stack <Node> s = new Stack <Node> ();
// declaring a current pointer
Node currentNode = root;
// traverse until the stack is not empty
while(s.empty() == false || currentNode != null) {
// if the currentNode is not null, push it into the stack
if(currentNode != null) {
s.push(currentNode);
// moving to the right subtree
currentNode = currentNode.right;
}
else {
// getting the top element of the stack
currentNode = s.pop();
// decrementing the value of k
k = k - 1;
if (k == 0) {
return currentNode.data;
}
// moving to the left subtree
currentNode = currentNode.left;
}
}
}Python code:
# defining a function that will return the Kth largest element in bst.
def KthLargestElement(root, k, n):
# checking the base case
if root is None:
return -1
# defining a stack
stack = []
# declaring a current pointer
currentNode = root
while len(stack) > 0 or currentNode != None:
# if the currentNode is None, push it into the stack
if currentNode != None:
stack.append(currentNode)
# moving to the right subtree
currentNode = currentNode.right
else:
# getting the top element of the stack
currentNode = stack.pop()
# decrementing the value of k
k = k - 1
if k == 0:
return currentNode.data
# moving to the left subtree
currentNode = currentNode.leftWhen the Input tree is:
10
/ \
4 20
/ / \
2 15 40And the given value of k is: 3
Output
The kth largest element of the binary search tree is: 15In the iterative revere in-order traversal approach to the problem – find the $k^{th}$ largest element in bst, we are traversing the input binary search tree only once using the in-order traversal of the binary search tree. We are also using an extra stack data structure.
Time Complexity
Since we are traversing the input binary search tree only once, the time complexity of the iterative revere in-order traversal approach to the problem – find the $k^{th}$ largest element in bst comes out to be O(n), where n is the size of the input binary search tree.
Space Complexity
Since we are using an extra stack to store the nodes, the space complexity of the iterative revere in-order traversal approach to the problem – find the kth largest element in bst comes out to be O(n), where n is the size of the stack (same as the number of nodes of the bst).
Approach 4: By using Reverse Morris Traversal
Before getting into the reverse morris traversal approach, let us first get a brief introduction to the Morris Traversal.
Morris traversal is a tree traversal algorithm (it can be in-order, pre-order, or post-order) that does not use any stack or recursion for the tree traversal.
Another efficient algorithm for the problem – find the kth largest element in bst is to perform the reverse Morris Traversal. So, we would traverse the tree in reverse order and decrement the value of k in each iteration. Once the value of k reaches 0, we have found our kth largest element in bst.
We can also use a counter that will increment in each traversal. Once the value of the counter is the same as k then we have found our answer.
Algorithm
The pseudo-code for the above-discussed algorithm can be:
- Initialize two pointers.
- The first pointer (
currentNode) will point to the root node. - The second pointer (
KthLargestNode) will point to NULL. - Perform the below steps until the
currentNodedoes not becomes NULL.- If the
currentNodehas no right child, increment the counter. - Check whether the value of
counteris the same askor not. - If it is the same then return the
currentNode‘s data as thekth largest element in bst. - Else, make the
currentNodepoint to its left subtree. - If the
currentNodehas the right child, then make thecurrentNodepoint to its right subtree. - Now we need to move the left child of the
currentNode, so we can use another pointer that will help us to traverse the leftmost child of thecurrentNode.- Move to the left-most child of the
currentNodeand let it be pointed by another pointer namelysuccessor. - Now check if the
successorhas no left child.- If the
successorhas no left child then make thesuccessor.leftpoint to thecurrentNodeand move thecurrentNodeto its right child. Else, increment the counter by1.- Again check whether the value of
counteris the same askor not. - If it is the same then return the
currentNode‘s data as thekth largest element in bst. Else, make thecurrentNodepoint to its left subtree.
- If the
- Move to the left-most child of the
- If the
Code Implementation
Let us code the above-discussed algorithm for better understanding.
C++ code:
// defining a function that will return the Kth largest element in bst.
int KthLargestUsingMorrisTraversal(Node *root, int k, int n) {
// initializing pointer
Node *currentNode = root;
Node *KthLargestNode = NULL;
// initializing the counter variable
int counter = 0;
while (currentNode != NULL) {
// if the right child is NULL, increment the counter and check
if (currentNode->right == NULL) {
counter = counter + 1;
if (counter == k)
KthLargestNode = currentNode;
// else, move to the left child
currentNode = currentNode->left;
}
else {
// initializing the successorNode.
Node *successorNode = currentNode->right;
// moving to the left-most node of successorNode
while (successorNode->left != NULL && successorNode->left != currentNode)
successorNode = successorNode->left;
if (successorNode->left == NULL) {
// making the successorNode point to currentNode
successorNode->left = currentNode;
// move to the left child of currentNode
currentNode = currentNode->right;
}
else {
successorNode->left = NULL;
// increasing the counter and checking
counter = counter + 1;
if (counter == k)
KthLargestNode = currentNode;
// move to the left child of currentNode
currentNode = currentNode->left;
}
}
}
// returning the required element
return KthLargestNode->data;
} Java code:
// defining a function that will return the Kth largest element in bst.
static int KthLargestElement(Node root, int k, int n) {
// initializing pointer
Node currentNode = root;
Node KthLargestNode = null;
// initializing the counter variable
int counter = 0;
while (currentNode != null) {
// if the right child is null, increment the counter and check
if (currentNode.right == null) {
counter = counter + 1;
if (counter == k)
KthLargestNode = currentNode;
// else, move to the left child
currentNode = currentNode.left;
}
else {
// initializing the successorNode.
Node successorNode = currentNode.right;
// moving to the left-most node of successorNode
while (successorNode.left != null && successorNode.left != currentNode)
successorNode = successorNode.left;
if (successorNode.left == null) {
// making the successorNode point to currentNode
successorNode.left = currentNode;
// move to the left child of currentNode
currentNode = currentNode.right;
}
else {
successorNode.left = null;
// increasing the counter and checking
counter = counter + 1;
if (counter == k)
KthLargestNode = currentNode;
// move to the left child of currentNode
currentNode = currentNode.left;
}
}
}
// returning the required element
return KthLargestNode.data;
}Python code:
# defining a function that will return the Kth largest element in bst.
def KthLargestElement(root, k, n):
# initializing pointer
currentNode = root
KthLargestNode = None
# initializing the counter variable
counter = 0
while (currentNode != None):
# if the right child is none, increment the counter and check
if (currentNode.right == None):
counter += 1
if (counter == k):
KthLargestNode = currentNode
# else, move to the left child
currentNode = currentNode.left
else:
# initializing the successorNode.
successorNode = currentNode.right
# moving to the left-most node of successorNode
while (successorNode.left != None and
successorNode.left != currentNode):
successorNode = successorNode.left
if successorNode.left == None:
# making the successorNode point to currentNode
successorNode.left = currentNode
# move to the left child of currentNode
currentNode = currentNode.right
else:
successorNode.left = None
# increasing the counter and checking
counter += 1
if (counter == k):
KthLargestNode = currentNode
# move to the left child of currentNode
currentNode = currentNode.left
return KthLargestNode.dataWhen the Input tree is:
10
/ \
4 20
/ / \
2 15 40And the given value of k is: 3
Output
The kth largest element of the binary search tree is: 15In the reverse morris traversal approach to the problem – find the kth largest element in bst, we are traversing the input binary search tree only once using the reverse morris traversal algorithm of the binary search tree. We are not using any extra space apart from a few pointers.
Time Complexity
Since we are traversing the input binary search tree only once, the time complexity of the reverse morris traversal approach to the problem – find the $k^{th}$ largest element in bst comes out to be O(n), where n is the size of the input binary search tree.
Space Complexity
Since we are not using any extra space, the space complexity of the reverse morris traversal approach to the problem – find the $k^{th}$ largest element in bst comes out to be O(1).
Approach 5: Efficient Approach – using Augmented BST
Before getting into the augment tree approach, let us first get a brief introduction to the Augmented Binary Search Trees.
An augment binary search tree is a special kind of bst which stores the data in sorted manner apart from that, it also keeps the track of some kind of information about the element based on which the elements of the bst have been stored.
So, another efficient algorithm for the problem – find the kth largest element in bst is to use the idea behind the augmented BSTs. The idea is very simple, we can keep track of the number of nodes present in the left subtree and the right subtree during the insertion of the node in the bst. As we need to find the kth largest element, we need to keep track of the elements present in the right subtree of the current node.
Note: Since we need to keep track of the number of right children of a node, we need to use another variable (rightNodes) in the structure of the binary search tree node itself.
Algorithm
The pseudo-code for the above-discussed algorithm can be:
- Initialize a pointer(
currentNode) that will point to the current root node. - Perform the below-mentioned steps until the
currentNodeis not NULL (None).- If the number of nodes present in the right subtree of any node is
nand the valuen + 1is the same as the value ofkthen the root element is our answer.
- If the number of nodes present in the right subtree of any node is
- Else if, the value of
nis greater than the value ofkthen we need to keep moving in the right subtree (using recursion). - Else (the value of
nis lesser than the value ofk) then need to keep moving in the left subtree (using recursion).
Code Implementation
Let us code the above-discussed algorithm for better understanding.
Structure of the BST node:
Node {
int data;
Node right;
Node left;
int rightCounter;
}C++ code:
// defining a function that will return the Kth largest element in bst.
int KthLargestUsingMorrisTraversal(Node *root, int k, int n) {
// checking the base case
if(root == NULL)
return -1;
if (root) {
Node* currentNode = root;
while (currentNode) {
if(currentNode->rightCounter + 1 == k) {
return currentNode->data;
}
else if(k > currentNode->rightCounter + 1) {
k = k - (currentNode->rightCounter + 1);
currentNode = currentNode->left;
}
else {
currentNode = currentNode->right;
}
}
}
return -1;
}Java code:
// defining a function that will return the Kth largest element in bst.
static int KthLargestElement(Node root, int k, int n) {
// checking the base case
if(root == null)
return -1;
if (root) {
Node currentNode = root;
while (currentNode != null) {
if(currentNode.rightCounter + 1 == k) {
return currentNode.data;
}
else if(k > currentNode.rightCounter + 1) {
k = k - (currentNode.rightCounter + 1);
currentNode = currentNode.left;
}
else {
currentNode = currentNode.right;
}
}
}
return -1;
}Python code:
# defining a function that will return the Kth largest element in bst.
def KthLargestElement(root, k, n):
# checking the base case
if root == None:
return -1
if root:
currentNode = root
while currentNode is not None:
if currentNode.rightCounter + 1 == k:
return currentNode.data
elif k > currentNode.rightCounter + 1:
k = k - (currentNode.rightCounter + 1)
currentNode = currentNode.left
else:
currentNode = currentNode.right
return -1When the Input tree is:
10
/ \
4 20
/ / \
2 15 40And the given value of k is: 3
Output
The kth largest element of the binary search tree is: 15In the augment tree approach to the problem – find the $k^{th}$ largest element in bst, we are traversing the input binary search tree only once. We are not using any extra space apart from a few pointers.
Time Complexity
Since we are traversing the input binary search tree only once, the time complexity of the augment tree approach to the problem – find the kth largest element in bst comes out to be O(n), where n is the size of the input binary search tree.
Space Complexity
Since we are not using any extra space, the space complexity of the augment tree approach to the problem – find the $k^{th}$ largest element in bst comes out to be O(1).
Note: There is O(h) space used for the recursion call stack, where h is the height of the binary search tree.
Conclusion
- A binary search tree can be defined as a collection of objects or elements or entities known as nodes. These nodes are linked together to represent a hierarchy.
- The top node of the hierarchy is known as the root node. Each node of a binary search tree contains some data and it can have at most two child nodes. The left child is always less than the parent node and the right child is always greater than the parent node.
- The brute force approach to find the $k^{th}$ largest element in bst, can be traversing the entire binary search tree using the in-order traversal algorithm and side-by-side storing the values.
- In the
brute forceapproach to finding the $k^{th}$ largest element in bst, the time complexity of the algorithm comes out to beO(n)and the space complexity also comes out to beO(n), wherenis the number of nodes in the binary tree.$k^{th}$ - Another approach to finding the $k^{th}$ largest element in bst, can be performing the recursive reverse in-order traversal of the binary search tree and decrementing the value of
kin each recursive call. - In the
reverse in-order traversalapproach to finding the $k^{th}$ largest element in bst, the time complexity of the algorithm comes out to beO(n), wherenis the number of nodes in the binary tree and the space complexity also comes out to beO(1). - Another approach to finding the $k^{th}$ largest element in bst, can be performing the iterative in-order traversal of the bst and storing the values into a stack data structure.
- In the
iterative in-order traversalapproach to finding the $k^{th}$ largest element in bst, thetime complexityof the algorithm comes out to beO(n)and the space complexity also comes out to beO(n), wherenis the number of nodes in the binary tree. - Another approach to finding the kth largest element in bst, can be performing the reverse Morris Traversal and decrementing the value of
kin each iteration. - In the
reverse Morris Traversalapproach to finding the $k^{th}$ largest element in bst, the time complexity of the algorithm comes out to beO(n), wherenis the number of nodes in the binary tree and the space complexity also comes out to beO(1). - Another approach to finding the $k^{th}$ largest element in bst, can be using the idea behind the augmented BSTs. We can keep track of the number of nodes present in the left subtree and the right subtree during the insertion of the node in the bst.
- In the
augmented BSTapproach to finding the $k^{th}$largest element in bst, the time complexity of the algorithm comes out to beO(n), wherenis the number of nodes in the binary tree and the space complexity also comes out to beO(1).