In graph theory, a cut is a set of edges removal of which divides a connected graph into two non-overlapping (disjoint) subsets. The minimum cut (or min-cut) is defined as the minimum number of edges, when removed from a graph, divide the graph into two disjoint sets.
A randomized contraction algorithm $i.e.$ Karger's Algorithm is used to find the minimum cut of a graph in data structure.
Scope of the Article.
- Concept of the cut and the
minimum cuthave been explained in detail through an example. Karger's algorithmto find the minimum cut of a graph have been explained along with a detailed example and codes in C/C++, and Java.
Takeaways
Karger's Algorithm is a randomized algorithm whose runtime is deterministic; that is, on every run, the time to execute will be bounded by a fixed time function in the size of the input but the algorithm may return a wrong answer with a small probability.
Introduction to Minimum Cut
Before discussing Minimum cut, let us first understand what does a Cut means in terms of graph data structure?
A cut can be defined as a partition of vertices of a graph into two or more disjoint subsets.
For example:
The given graph $G$ has $5$ vertices and $6$ edges –
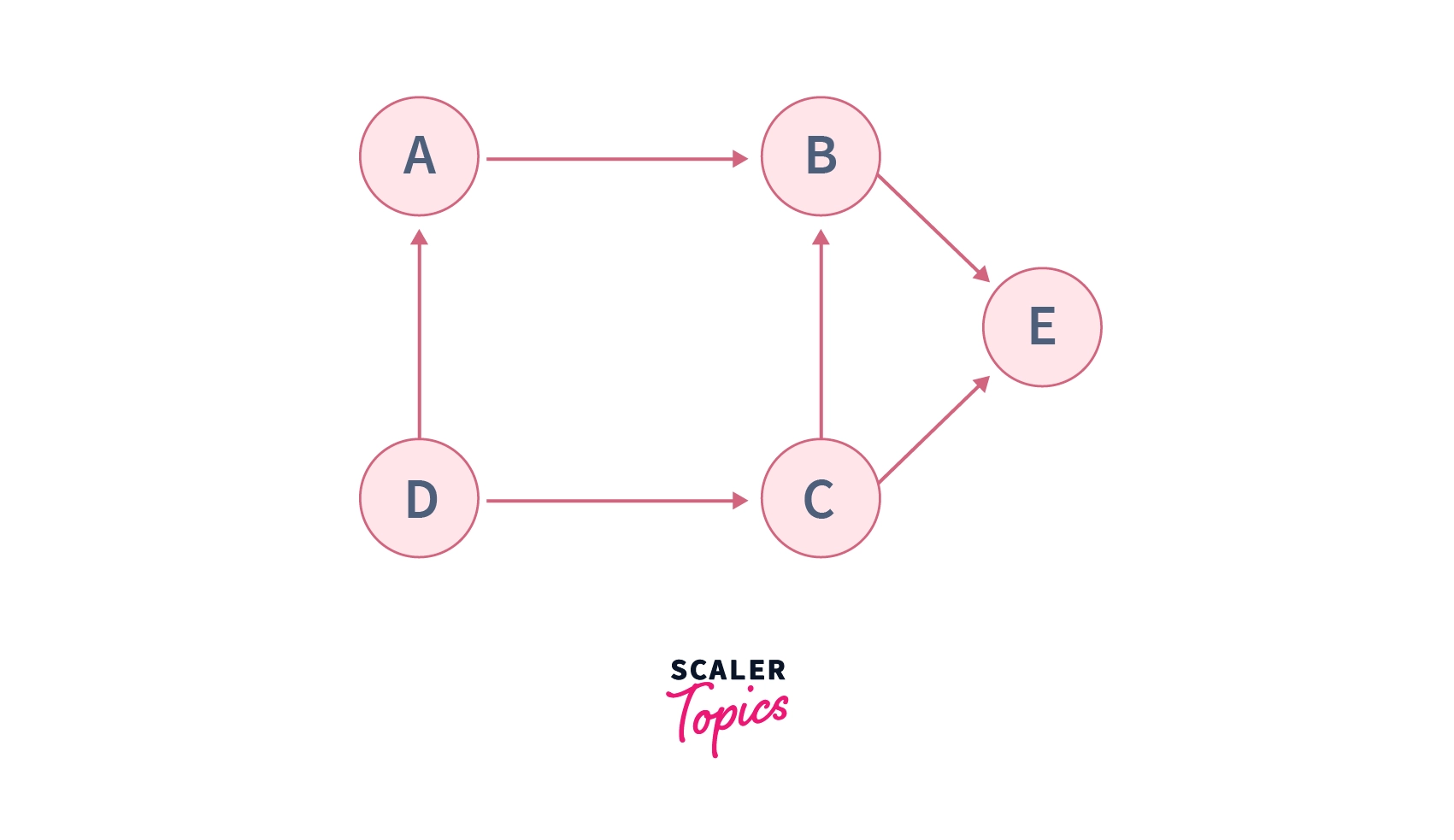
One of the possible cuts in this graph is to partition this graph into two disjoint sets $i.e.$ splitting the graph into two disconnected components, one with vertices $A, B, C \space and\space D$ and the other one with a single vertex $E$ by removing three edges $B\leftrightarrow C,$ $B\leftrightarrow E,$ and $C\leftrightarrow E$ as shown below –
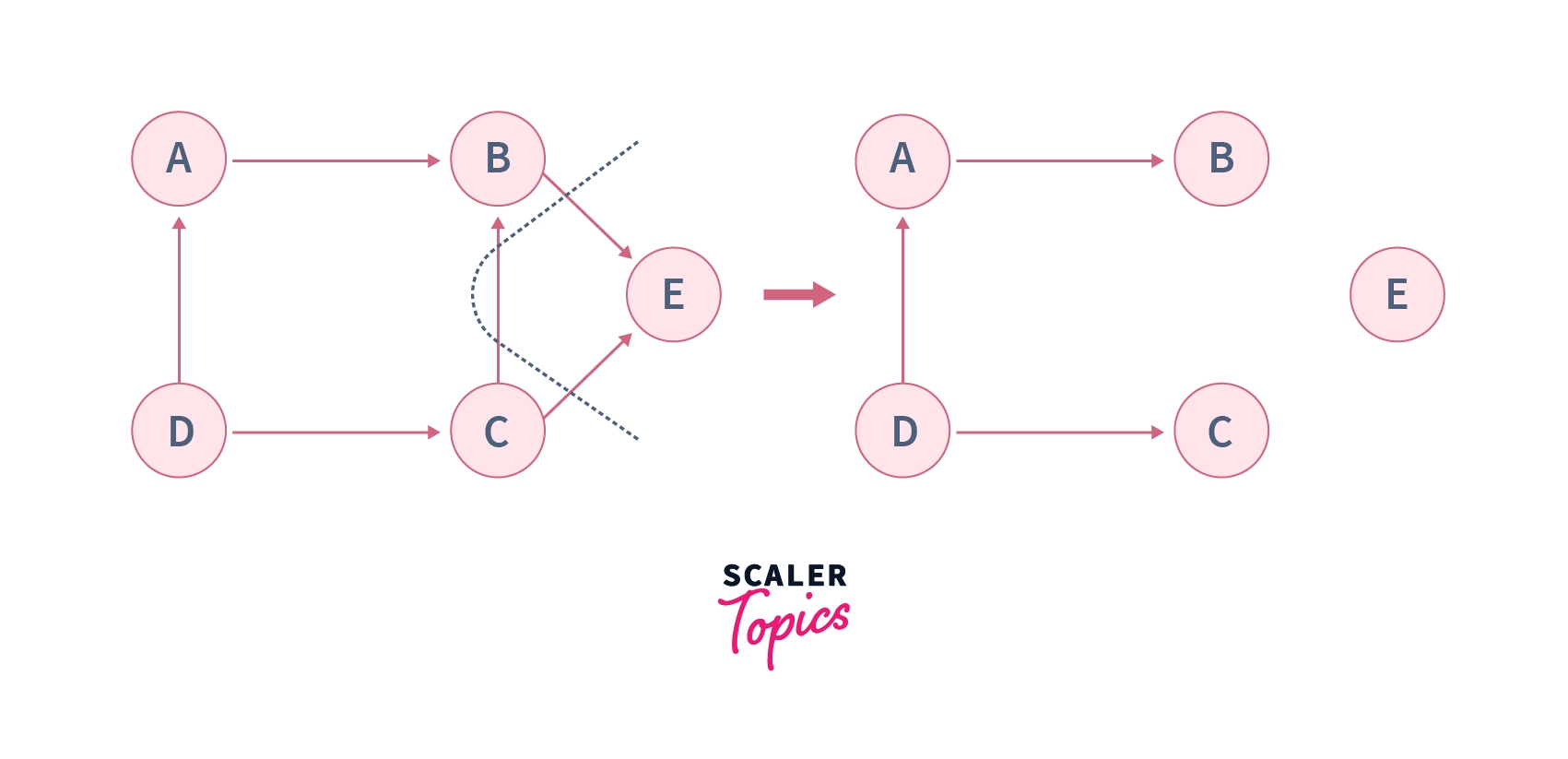
Each cut has some size associated with it, that is the sum of the weights of the edges that have been removed. In the case of un-weighted graphs size is nothing but the number of vertices that have been removed.
Now as suggested by the name, A Minimum cut (or simply a min-cut) of a graph $G$ can be defined as cut with minimum size $i.e.$ there is no other possible cut in the graph $G$ with a smaller size.
In simple words, the minimum number of edges required to remove to disconnect the graph into two components is known as the minimum cut of the graph.
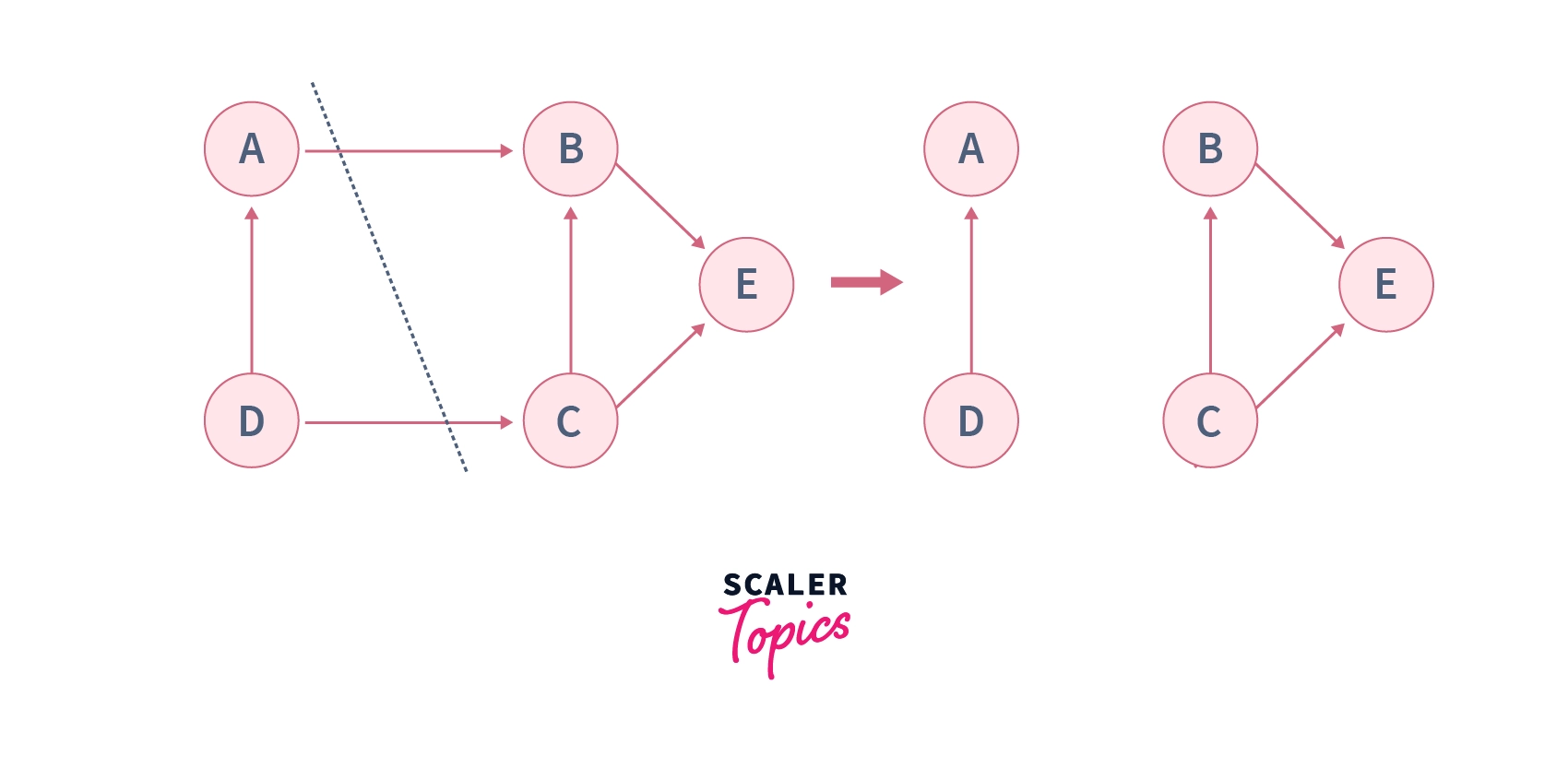
The min-cut of the above-shown graph is shown below which can be obtained by removing two edges, $A\leftrightarrow B$ and $D\leftrightarrow C$.
Karger’s Algorithm to Find Min Cut
Karger's algorithm is a randomized algorithm (an algorithm which have some degree of randomness associated in its procedure) to compute a minimum cut of a connected, undirected, and unweighted graph $G=(V,E)$. It is a “Monte Carlo” algorithm which means it may also produce a wrong output with a certain (usually low) probability.
The main idea of Karger’s algorithm is based on the concept of edge contraction, where edge contraction means merging two nodes (say $u$ and $v$) of the graph $G$ into one node which is also termed as a supernode. All the edges connecting either to $u$ or $v$ are now attached to the merged node (supernode) which may result in a multigraph as shown in the image given below –
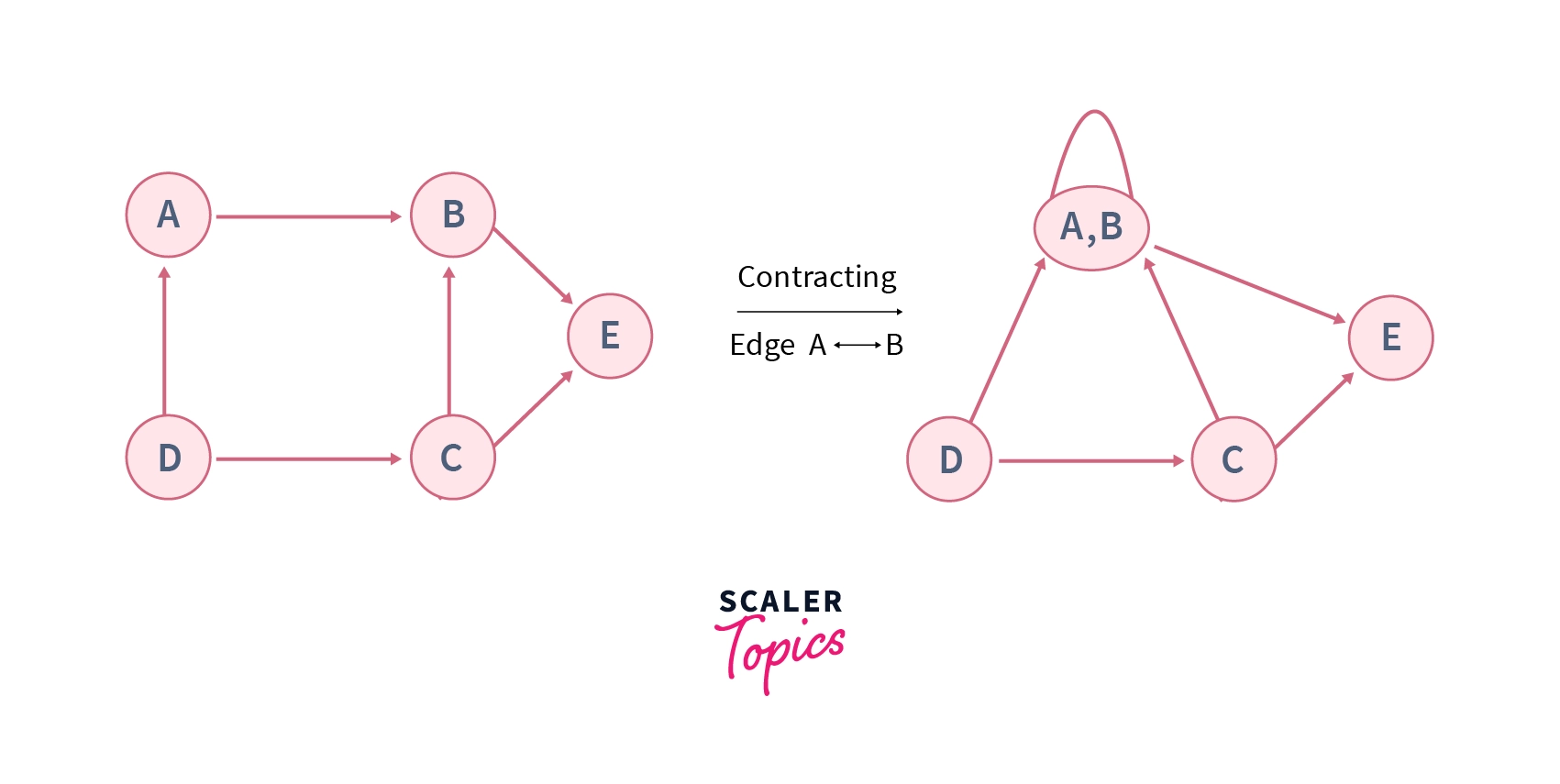
In Karger's algorithm, an edge is chosen randomly, and then the chosen edge is contracted which results in a supernode. The process continues until only two supernodes are remaining in the graph. Those two supernodes represent cut in the original graph $G$.
As Karger algorithm being a "Monte Carlo" algorithm can also give wrong answers so by repeating the algorithm many times the minimum cut of the graph can be found with a certainly high probability.
Algorithm
- Make a copy of graph $G$ which will be termed as $CG$ (contracted graph).
- While $CG$ contains more than two vertices
- Select any random edge $u\leftrightarrow v$ from the contracted graph.
- Contract the edge and merge the vertices $u$ and $v$ into one.
- Remove self-loops (if formed).
- After the above step only two vertices will be remaining in the graph and the edges connecting those two vertices represents the minimum cut of the graph.
Now let us understand how this algorithm finds the minimum cut through an example.
Example
Let $G$ be the given undirected graph with $5$ vertices and $7$ edges for which we are interested to calculate minimum cut –
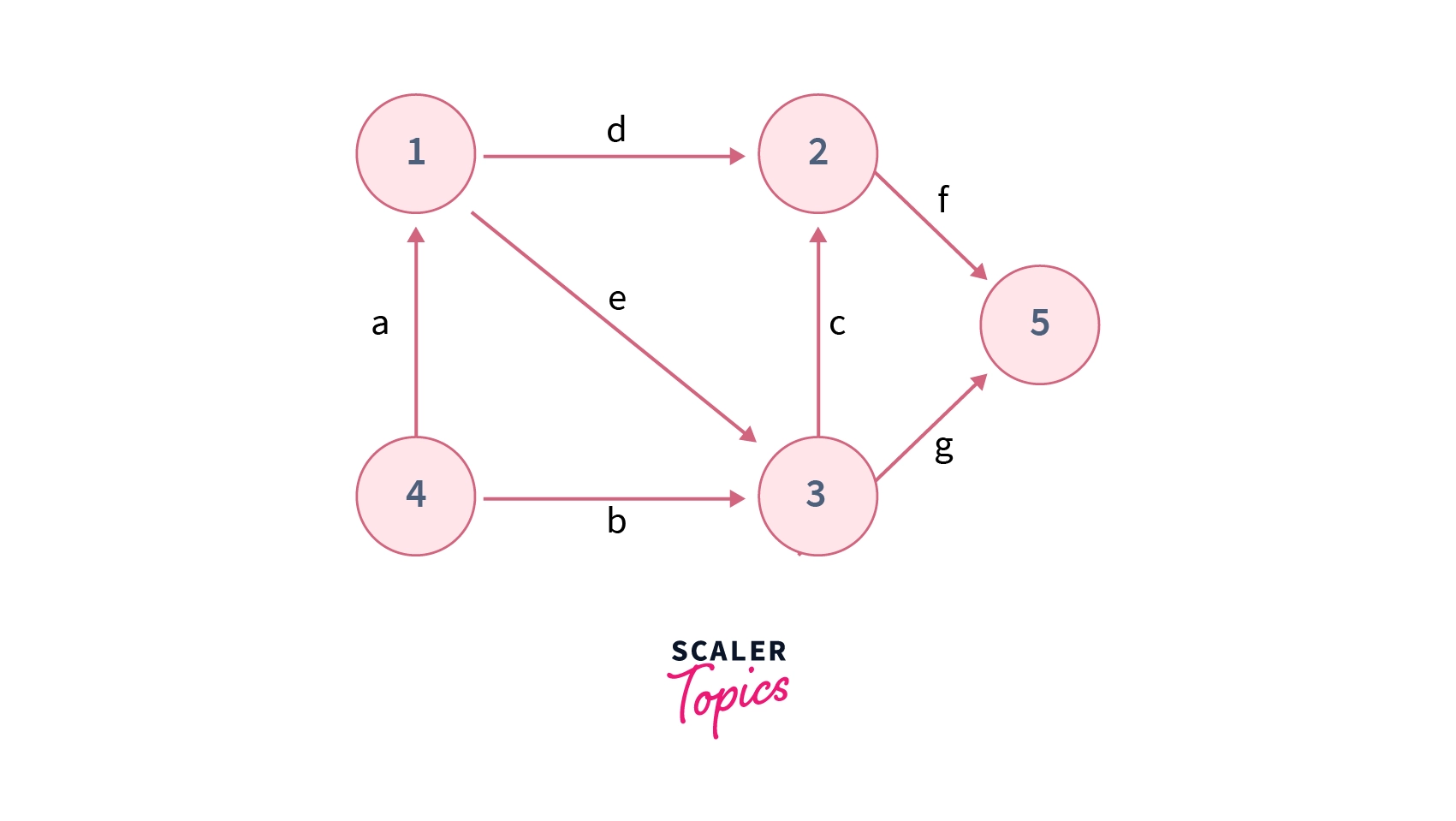
Step 1 – We choose edge $a$ to contract, nodes $1$ and $4$ will be merged into one supernode and all edges connecting them will be adjusted accordingly. Then the contracted graph will look like :
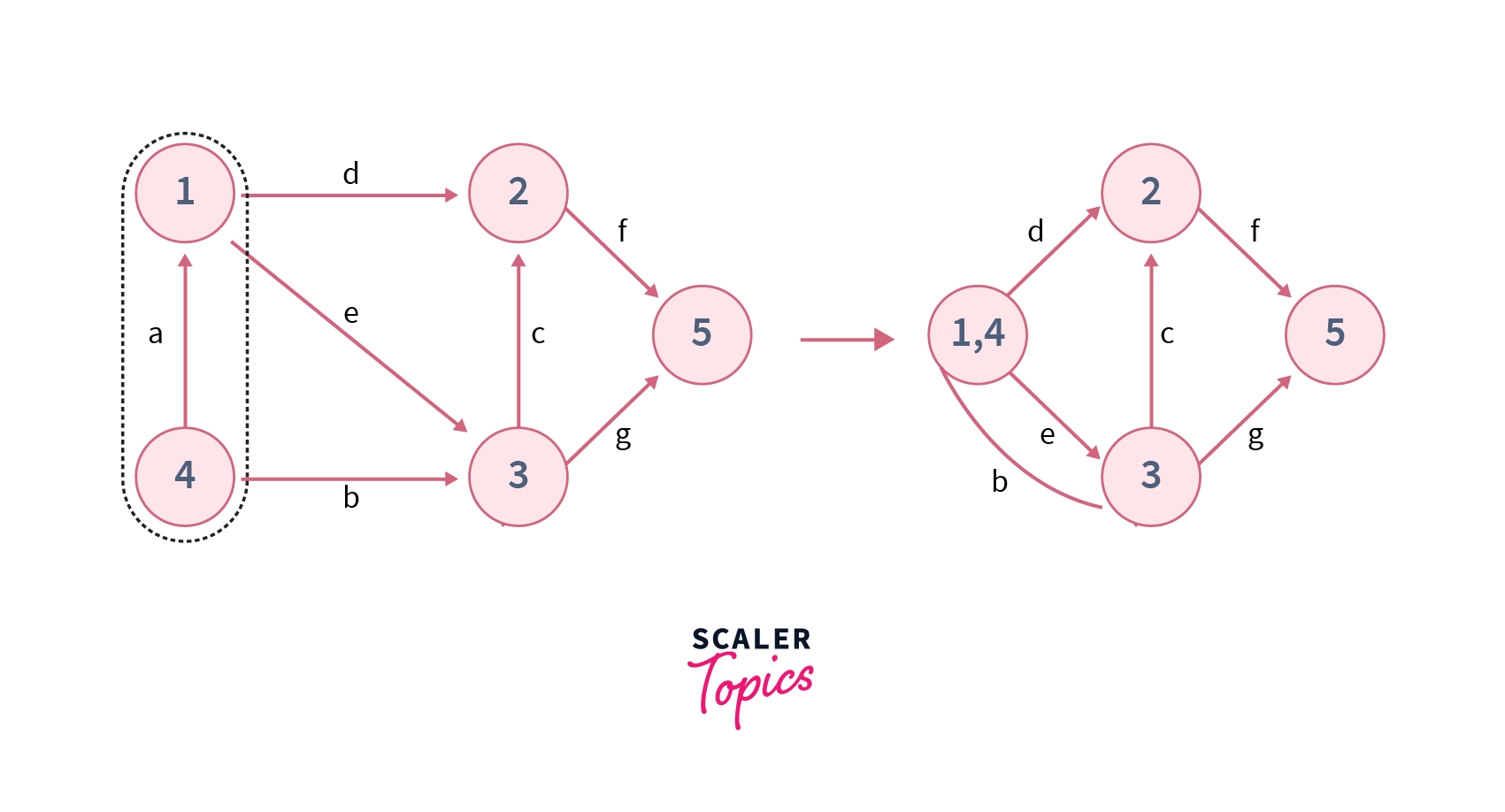
Step 2– This time we select the edge $c$ for contracting, so nodes $2$ and $3$ will be merged and after merging endpoints of the edge $c$, the contracted graph $(CG)$ will look like
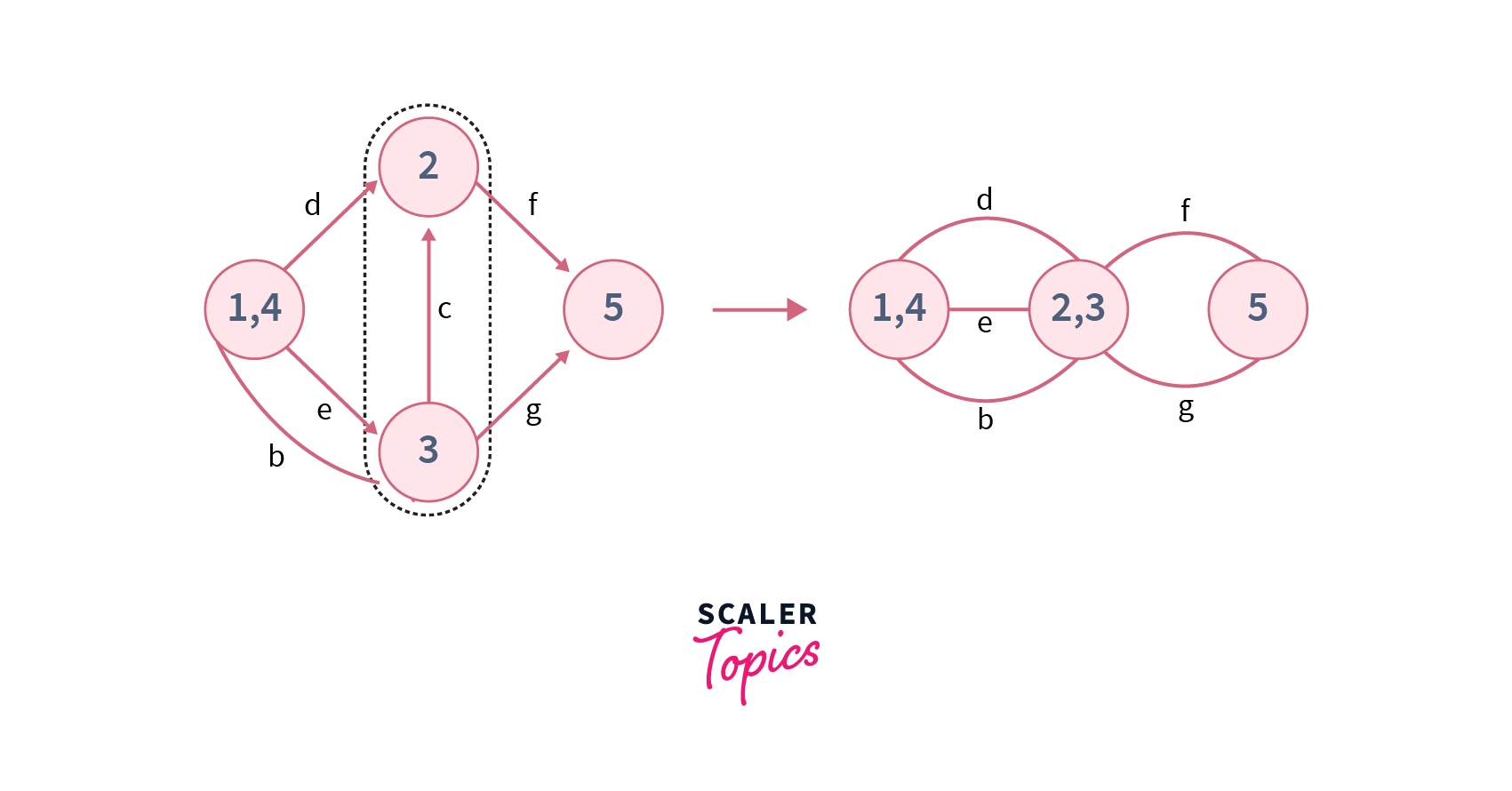
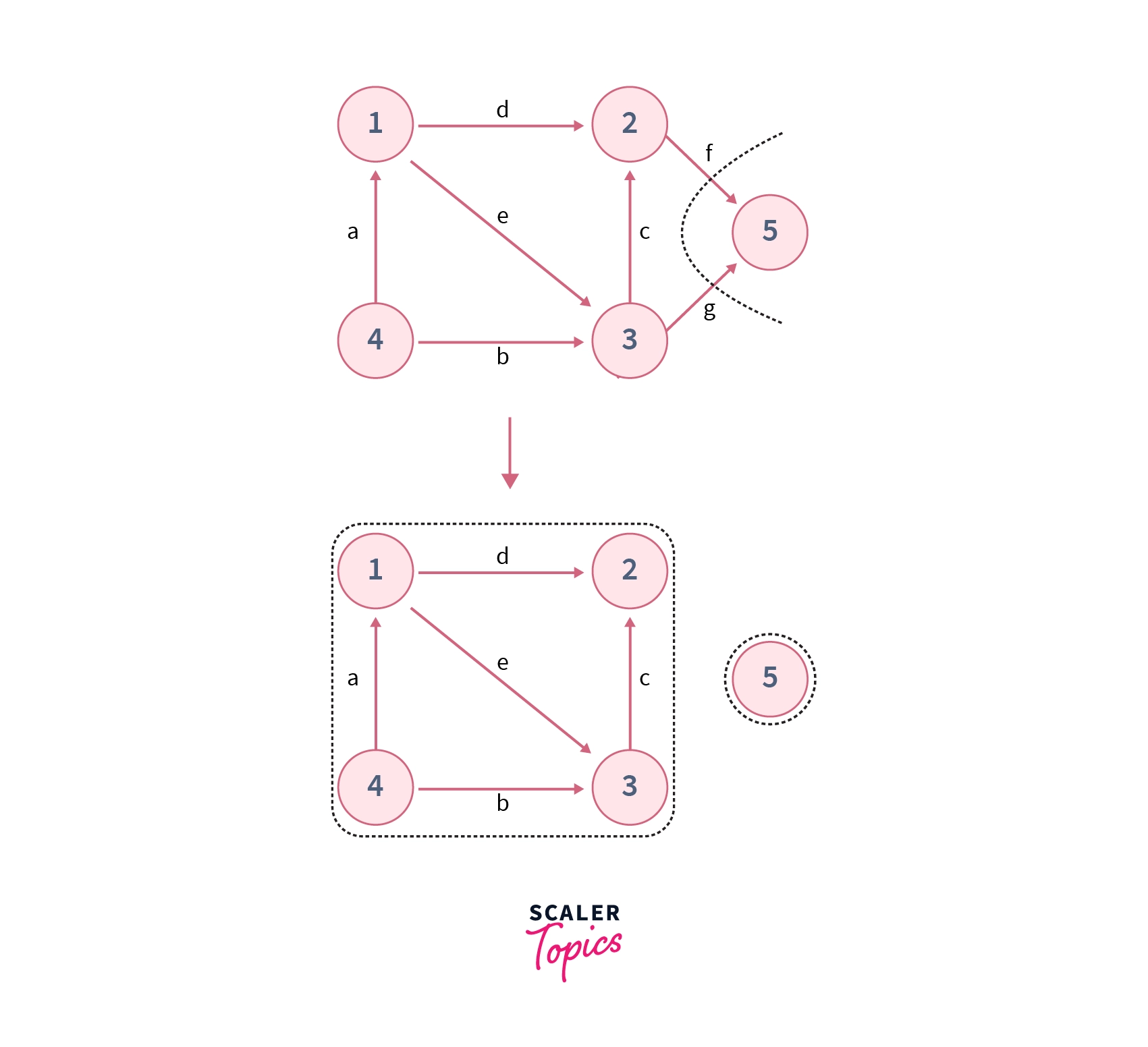
Step 3 – Now in our contracted graph, we choose edge $e$ for contracting hence supernodes ${1,4}$ and ${2,3}$ will get merged, and edges $f$ and $g$ will get attached to resultant supernode ${1, 4, 2, 3}$.
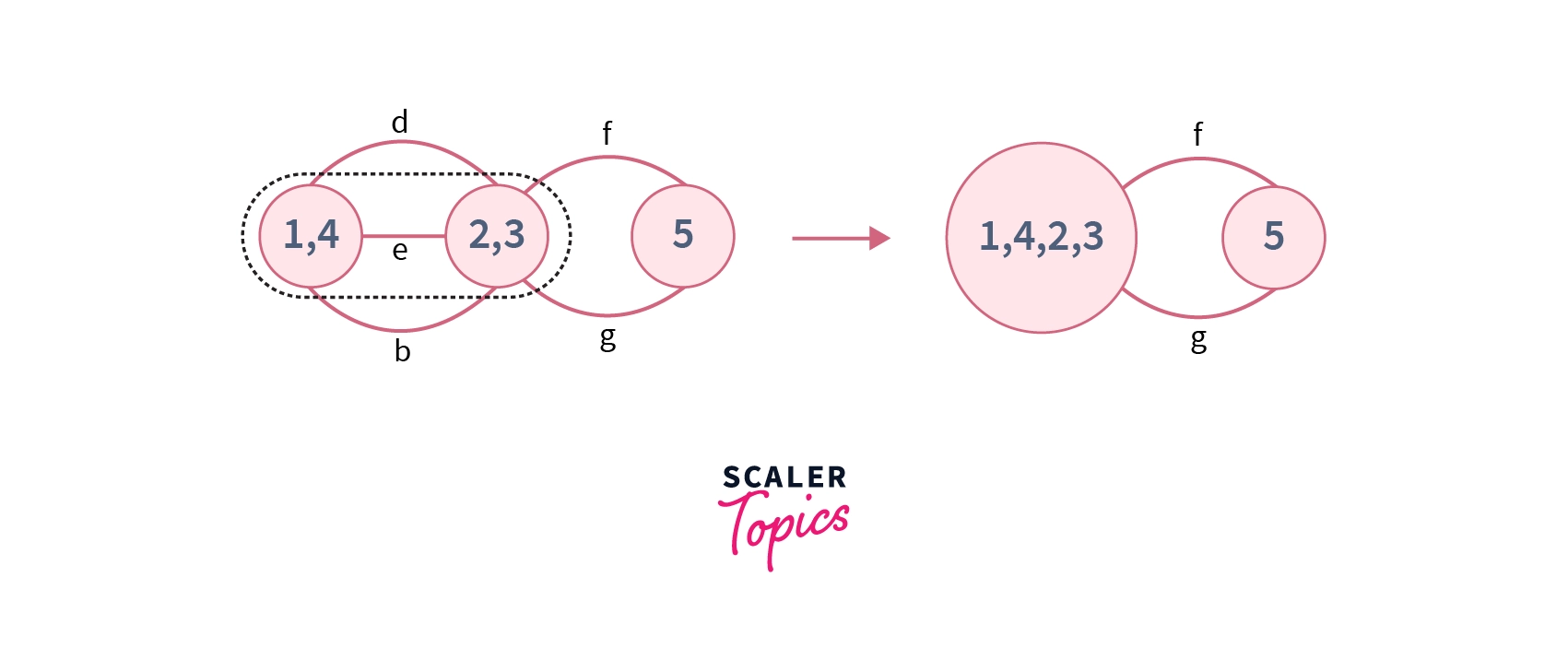
Now our resultant contracted graph contains only two vertices so this is the minimum cut. We can remove edges $f$ and $g$ to disconnect the graph into two components which is also verified by removing them in the original graph in the diagram shown below –
Pseudocode
In DSU article we have seen how we can keep record of the sets to which a particular element belongs in almost constant time complexity.
We use the same concept here, to keep track of vertices that belongs to a particular supernode using $find(node)$ operation and contracting an edge $u\leftrightarrow v$ using $union(u, v)$ operation.
In the underlying pseudocode $edges$ denotes the list of all the edges of graph $G,$ $V$ and $E$ represents number of vertices and edges present in it respectively.
MinCut(edges, V, E):
vertices=V
While(vertices > 2):
i=Random integer in the range [0,E-1]
set_1=find(edges[i].u)
set_2=find(edges[i].v)
if(set_1 != set_2):
vertices = vertices-1
Union(u, v)
ans=0
For(i in the range 0 to E-1):
set_1=find(edges[i].u)
set_2=find(edges[i].v)
if(set_1 != set_2):
ans = ans + 1
Return ansCode
Before seeing the code of Karger's algorithm let’s see the blueprint of the code $i.e.$ how we are implementing it, what are data members and methods we are using, etc.
Input –
A array/list of edges of the graph $G$, where $edge[i]$ is pair of vertices ${u,v}.$
Expected Output –
Size of minimum cut of the graph.
Data Members –
- $V$ – Represents the number of vertices in the graph.
- $E$ – Represents the number of edges in the graph.
- $parent$ – A integer type array, (Please refer implementation of DSU for detailed explanation)
- $rank$ – A integer type array, (Please refer implementation of DSU for detailed explanation) Methods –
minCut– It is the main function used to find the minimum cut of the graph by contracting the edges of the graph $G$ till we have been left with only two vertices.Find– It is used to check whether two nodes belong to the same supernode or not by checking if the leader of set to which vertices $u$ and $v$ belongs is same or not.Union– It is used to merge two nodes into one supernode by using the typical union function as discussed in theDSUarticle.
C/C++ implementation of Karger’s Algorithm
#include<bits/stdc++.h>
using namespace std;
// Edge class
class Edge{
public:
// Endpoints u and v
// of the Edge e.
int u;
int v;
// Dummy Constructor
Edge(){};
// Constructor for
// Initializing values.
Edge(int U,int V){
u=U;
v=V;
}
};
class MinCut{
public:
// Declaring data members
// V, E, parent, and rank.
int V,E;
int *parent;
int *rank;
// Random module to get
// random integer values.
// Constructor
MinCut(int v, int e){
// Initializing data members.
V=v;
E=e;
parent=new int[V];
rank=new int[V];
// Initializing parent's and
// rank's by is and 0s.
for(int i=0;i<V;i++)
{
parent[i]=i;
rank[i]=0;
}
}
// Function to find minimum cut.
int minCutKarger(Edge edges[]){
int vertices=V;
// Iterating till vertices are
// greater than 2.
while(vertices>2)
{
// Getting a random integer
// in the range [0, E-1].
int i=rand()%E;
// Finding leader element to which
// edges[i].u belongs.
int set1=find(edges[i].u);
// Finding leader element to which
// edges[i].v belongs.
int set2=find(edges[i].v);
// If they do not belong
// to the same set.
if(set1!=set2)
{
cout<<"Contracting vertices "<<edges[i].u<<" and "<<edges[i].v<<endl;
// Merging vertices u and v into one.
Union(edges[i].u,edges[i].v);
// Reducing count of vertices by 1.
vertices--;
}
}
cout<<"Edges needs to be removed - "<<endl;
// Initializing answer (minCut) to 0.
int ans=0;
for(int i=0;i<E;i++)
{
// Finding leader element to which
// edges[i].u belongs.
int set1=find(edges[i].u);
// Finding leader element to which
// edges[i].v belongs.
int set2=find(edges[i].v);
// If they are not in the same set.
if(set1!=set2)
{
cout<<edges[i].u<<" <----> "<<edges[i].v<<endl;
// Increasing the ans.
ans++;
}
}
return ans;
}
// Find function
int find(int node){
// If the node is the parent of
// itself then it is the leader
// of the tree.
if(node==parent[node]) return node;
//Else, finding parent and also
// compressing the paths.
return parent[node]=find(parent[node]);
}
// Union function
void Union(int u,int v){
// Make u as a leader
// of its tree.
u=find(u);
// Make v as a leader
// of its tree.
v=find(v);
// If u and v are not equal,
// because if they are equal then
// it means they are already in
// same tree and it does not make
// sense to perform union operation.
if(u!=v)
{
// Checking tree with
// smaller depth/height.
if(rank[u]<rank[v])
{
int temp=u;
u=v;
v=temp;
}
// Attaching lower rank tree
// to the higher one.
parent[v]=u;
// If now ranks are equal
// increasing rank of u.
if(rank[u]==rank[v])
rank[u]++;
}
}
};
int main(){
// Define V and E beforehand
int V=5,E=7;
// Create an Object of
// class MinCut.
MinCut minCut(V,E);
// Make an array of edges by giving
// endpoints of the edge.
Edge *edge=new Edge[E];
edge[0]=Edge(0,3);
edge[1]=Edge(3,2);
edge[2]=Edge(2,1);
edge[3]=Edge(1,0);
edge[4]=Edge(0,2);
edge[5]=Edge(2,4);
edge[6]=Edge(4,1);
// Finding the size of the minimum cut.
cout<<"Count of edges needs to be removed "<<minCut.minCutKarger(edge)<<endl;
return 0;
}Java implementation of Karger’s Algorithm
// Importing necessary
// modules for Input/Output.
import java.util.*;
class MinCut{
// Declaring data members
// V, E, parent, and rank.
static int V,E;
static int parent[];
static int rank[];
// Random module to get
// random integer values.
static Random rand;
// Constructor
MinCut(int V, int E){
// Initializing data members.
this.V=V;
this.E=E;
parent=new int[V];
rank=new int[V];
rand = new Random();
// Initializing parent's and
// rank's by is and 0s.
for(int i=0;i<V;i++)
{
parent[i]=i;
rank[i]=0;
}
}
// Function to find minimum cut.
static int minCutKarger(Edge edges[]){
int vertices=V;
// Iterating till vertices are
// greater than 2.
while(vertices>2)
{
// Getting a random integer
// in the range [0, E-1].
int i=rand.nextInt(E);
// Finding leader element to which
// edges[i].u belongs.
int set1=find(edges[i].u);
// Finding leader element to which
// edges[i].v belongs.
int set2=find(edges[i].v);
// If they do not belong
// to the same set.
if(set1!=set2)
{
System.out.println("Contracting vertices "+edges[i].u+" and "+edges[i].v);
// Merging vertices u and v into one.
union(edges[i].u,edges[i].v);
// Reducing count of vertices by 1.
vertices--;
}
}
System.out.println("Edges needs to be removed - ");
// Initializing answer (minCut) to 0.
int ans=0;
for(int i=0;i<E;i++)
{
// Finding leader element to which
// edges[i].u belongs.
int set1=find(edges[i].u);
// Finding leader element to which
// edges[i].v belongs.
int set2=find(edges[i].v);
// If they are not in the same set.
if(set1!=set2)
{
System.out.println(edges[i].u+" <----> "+edges[i].v);
// Increasing the ans.
ans++;
}
}
return ans;
}
// Find function
public static int find(int node){
// If the node is the parent of
// itself then it is the leader
// of the tree.
if(node==parent[node]) return node;
//Else, finding parent and also
// compressing the paths.
return parent[node]=find(parent[node]);
}
// Union function
static void union(int u,int v){
// Make u as a leader
// of its tree.
u=find(u);
// Make v as a leader
// of its tree.
v=find(v);
// If u and v are not equal,
// because if they are equal then
// it means they are already in
// same tree and it does not make
// sense to perform union operation.
if(u!=v)
{
// Checking tree with
// smaller depth/height.
if(rank[u]<rank[v])
{
int temp=u;
u=v;
v=temp;
}
// Attaching lower rank tree
// to the higher one.
parent[v]=u;
// If now ranks are equal
// increasing rank of u.
if(rank[u]==rank[v])
rank[u]++;
}
}
// Edge class
static class Edge{
// Endpoints u and v
// of the Edge e.
int u;
int v;
// Constructor for
// Initializing values.
Edge(int u,int v){
this.u=u;
this.v=v;
}
}
// Driver Function
public static void main(String args[]){
// Define V and E beforehand
int V=5,E=7;
// Create an Object of
// class MinCut.
MinCut minCut=new MinCut(V,E);
// Make an array of edges by giving
// endpoints of the edge.
Edge edge[]=new Edge[E];
edge[0]=new Edge(0,3);
edge[1]=new Edge(3,2);
edge[2]=new Edge(2,1);
edge[3]=new Edge(1,0);
edge[4]=new Edge(0,2);
edge[5]=new Edge(2,4);
edge[6]=new Edge(4,1);
// Finding the size of the minimum cut.
System.out.println("Count of edges needs to be removed "+ MinCut.minCutKarger(edge));
}
}Output –
Contracting vertices 0 and 2
Contracting vertices 1 and 0
Contracting vertices 0 and 3
Edges needs to be removed -
2 <----> 4
4 <----> 1
Count of edges needs to be removed 2Complexity of Karger’s Algorithm
The time complexity of Karger's algorithm for a graph $G$ with $V$ vertices and $E$ edges when it is implemented by using the most optimized DSU approach is $O(E*\alpha(V))$ because in every iteration we are contracting the edges in the contracted graph.
Now as we learned in DSU for $V<10^{600},$ $O(\alpha(V))\simeq O(1)$. So we can write $O(E*\alpha(V))$ $=$ $O(E)$ and since maximum number of edges in a graph is order of $V^2$ therefore in terms of $V$ time complexity can be rewritten as $O(V^2)$.
The probability that cut produced by Karger's algorithm is the required min-cut of the graph is greater than or equal to $1/n^2$ which might seem very small.
We can improve this probability to an arbitrarily large probability, by repeating the algorithm several times and keeping track of values of size of cut found in each iteration.
To implement DSU we need an array of size $V$ hence the space complexity is $O(V)$.
Applications of the Minimum Cut
- It can be used to get an idea about the reliability of a network $i.e.$ smallest number of links failure of which will lead to failure of the entire network.
- In wartime, to know what is the minimum number of roads needed to be destroyed to block connectivity of an area from other parts of the enemy nation.
- It is used in image segmentation $i.e.$ separating foreground and background of an image.
Conclusion.
- The minimum number of edges needed to be removed to disconnect a connected, unweighted, undirected graph into two components denotes the size of the minimum cut of the graph.
Karger's algorithmis a randomized algorithm that takes $O(V^2)$ time to find the minimum cut of a graph with a certain probability.Minimum cutfinds its application in various domains such as network optmizations, image segmenation etc.