In the iterative inorder traversal of a binary tree, nodes are visited in the left, root, right sequence without using recursion. This traversal, which uses a stack for managing node sequence, is a key approach in processing binary trees, characterized by their two-node structure. We’ll explore how this method works and analyze its time and space complexity, illustrated with examples.
Nature of Recursion in DFS Transversals
Before learning the iterative inorder traversal, let’s see how the recursive calls are done in the DFS traversals of a binary tree.
We visit a node three times in a DFS traversal.
First: We visit the node coming from the top. We process the node at this instance when doing preorder traversal.
Second: We visit the node when recursion backtracks after visiting every node in the left subtree. When doing the inorder traversal, we process the node at this stage.
Third: Similarly, when we visit the node after visiting every node in the right subtree. When doing the post-order traversal we process the node at this stage.
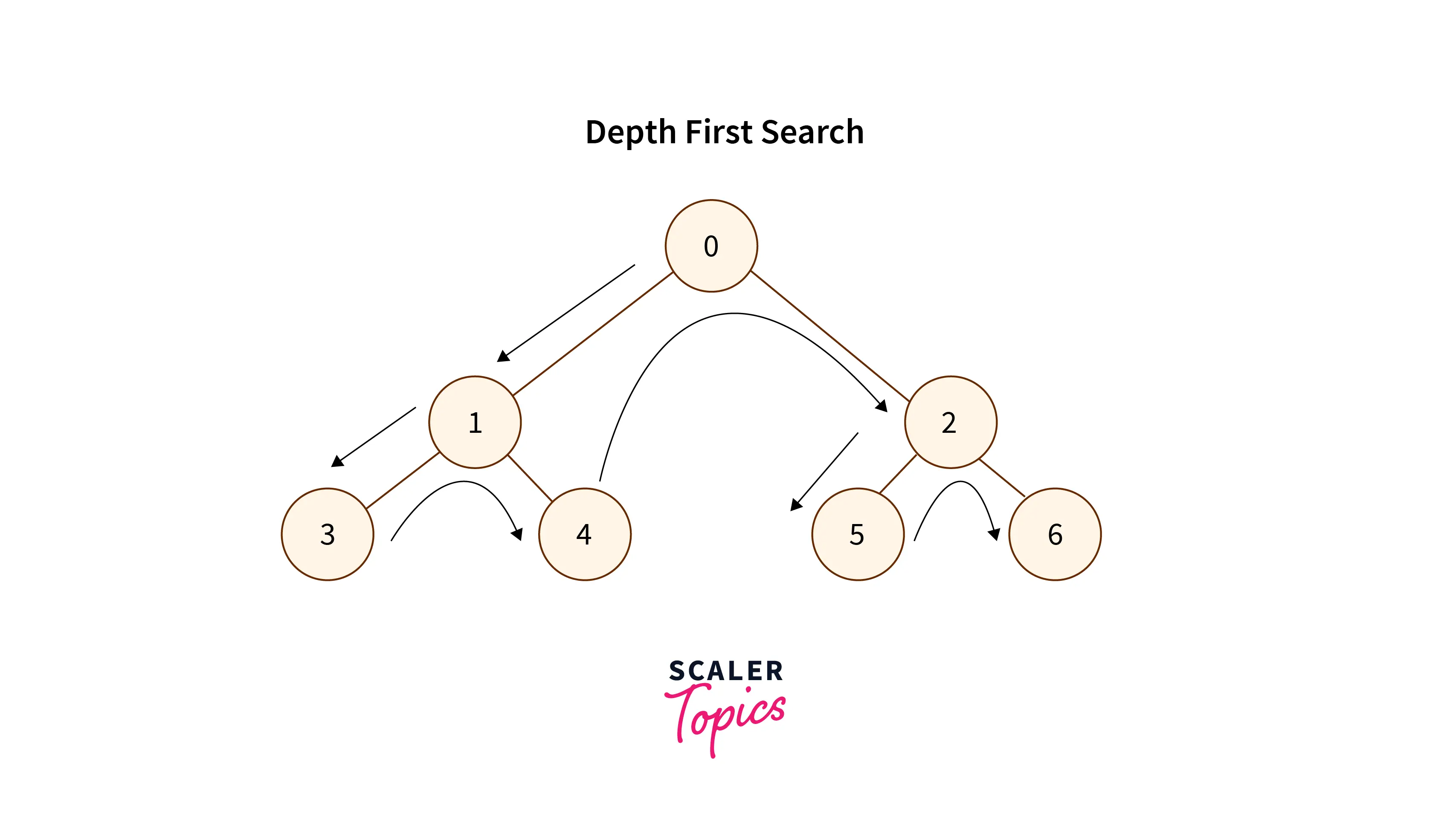
The Flow of recursion:
- Start from the root node and go to its left subtree, then go to the root of the left subtree, and in this way go to the leftmost node of the left subtree and process it.
- After processing the leftmost node, it backtracks to its root node and processes it, then visit the right subtree if any else backtracks to one level above in the tree hierarchy.
- If the leftmost node has only the right child, then recursion goes to the right child and processes the right subtree according to the inorder fashion, and after processing this, it recursion backtracks and traverses the tree similarly.
Inorder Tree Traversal – Iterative
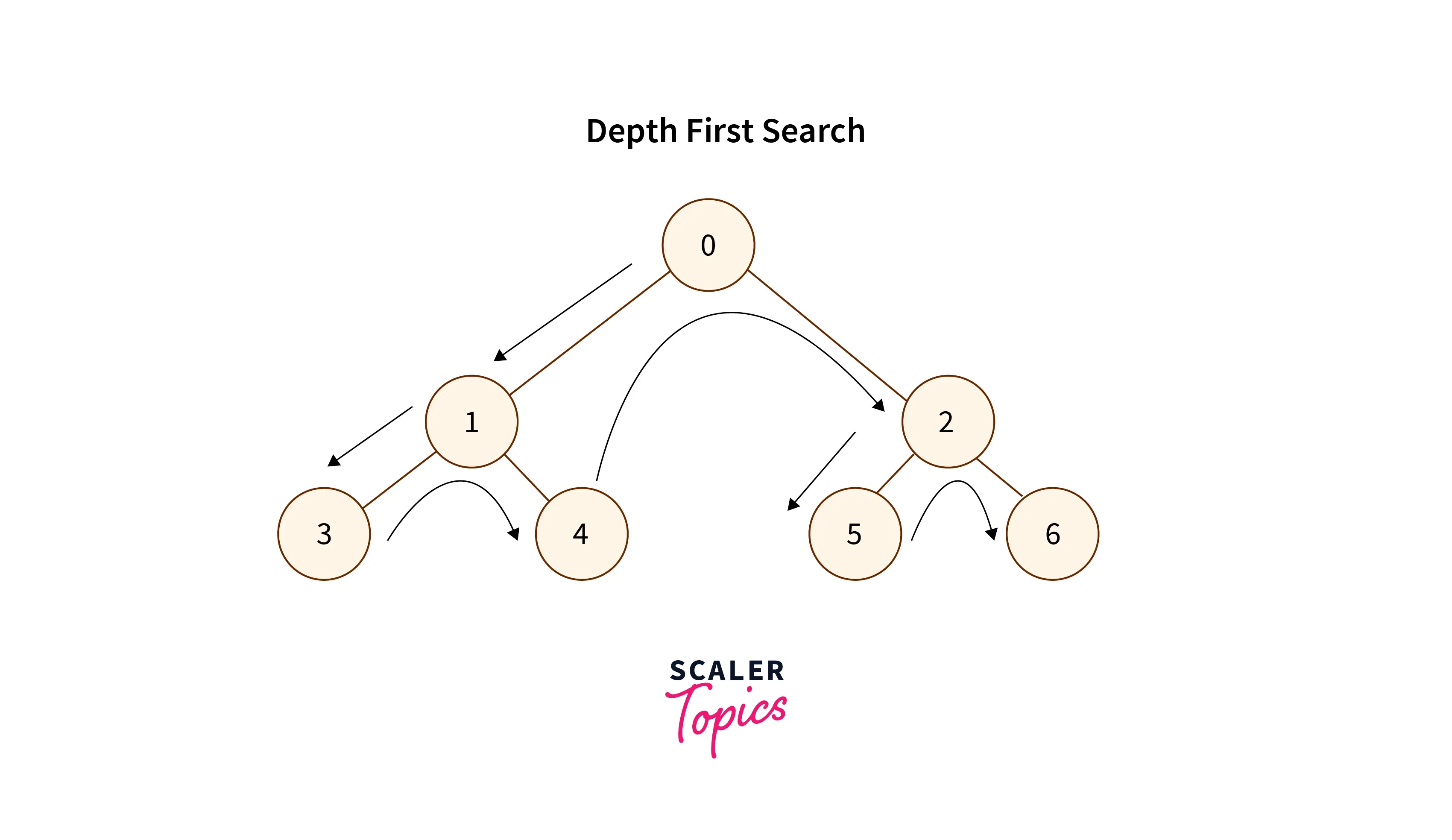
- So, let’s see the flow of how we can do the iterative inorder traversal.
- To do iterative inorder traversal we will use the stack data structure.
- We create an empty stack and push the root node to it.
- Create a pointer to hold the position of the current Node and initialize it with the root node. currentNode = root
- Now, run a loop till stack is not empty or currentNode != NULL
- We push the currentNode to the stack so that we can process the currentNode and the right subtree after processing the left subtree.
- Now we assign currentNode = currentNode -> left, we do this step iteratively till we reach the leftmost node, i.e. currentNode == NULL.
- If currentNode == NULL and the stack is not empty do the following steps: a) We pop the top element of the stack and assign currentNode = popped element -> right. b) now we print the popped element. c) now repeat the above step to process the left subtree
- If currentNode == NULL and the stack is empty then we have traversed the tree.
Algorithm for Iterative Inorder Traversal:
- Create an empty stack treeStack.
- Initialize currentNode as root.
- Push the currentNode to treeStack and set currentNode = currentNode->left until current is NULL
- If currentNode is NULL and treeStack is not empty then a) Pop the top element from treeStack. b) Print the popped element, set currentNode = popped element->right c) Go to step 3.
- If currentNode is NULL and treeStack is empty then we are done.
Let’s see with an example and understand step by step how the iterative inorder traversal works:
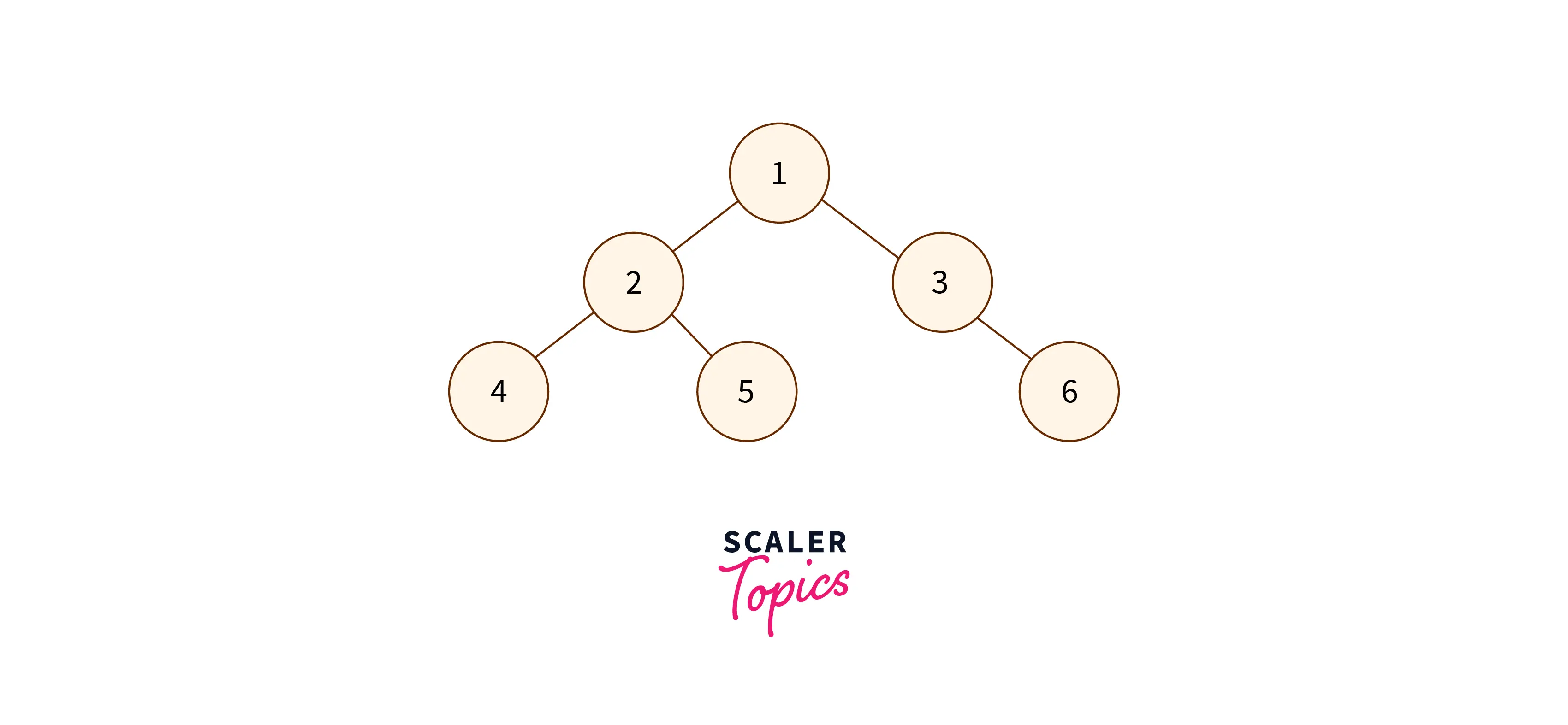
Consider the following binary tree:
Below is the steps to do iterative inorder traversal using the above algorithm:
Step 1 Creates an empty stack: treeStack = NULL
Step 2 sets current as address of root: currentNode = 1
Step 3 Pushes the current node and set current = current->left until current is NULL
currentNode = 1
push 1: treeStack -> 1
currentNode = 2
push 2: treeStack -> 2, 1
currentNode = 4
push 4: treeStack -> 4, 2, 1
currentNode = NULL
Step 4 pops from S
a) Pop 4: treeStack -> 2, 1
b) print "4"
c) currentNode = NULL and go to step 3
Since current is NULL step 3 doesn't do anything.
Step 4 pop again
a) Pop 2: treeStack -> 1
b) print "2"
c) currentNode = 5, as right of 2 is 5 and go to step 3
Step 3 pushes 5 to stack and makes currentNode NULL
treeStack -> 5, 1
currentNode = NULL
Step 4 pops from treeStack
a) Pop 5: treeStack -> 1
b) print "5"
c) currentNode = NULL as 5 is a leaf node and go to step 3
Since current is NULL step 3 doesn't do anything
Step 4 pop again
a) Pop 1: treeStack -> NULL
b) print "1"
c) currentNode = 3, right child of 1 is 3
Step 3 pushes 3 to treeStack and makes currentNode as NULL
treeStack -> 3
currentNode = NULL
Step 4 pops from treeStack
a) Pop 3: Stack S -> NULL
b) print "3"
c) currentNode = 6 right of 3 is 6
Step 3 pushes 6 to treeStack and makes currentNode as NULL
treeStack -> 6
currentNode = NULL, as right of 6 is null
Step 4 pops from treeStack
a) Pop 6: treeStack -> NULL
b) print "6"
c) currentNode = NULL
Now, as treeStack is empty and currentNode == NULL, therefore the traversal is completed.
Iterative inorder traversal order: 4,2,5,1,3,6
C++ program for iterative inorder traversal
#include<bits/stdc++.h>
using namespace std;
/* binary tree node data structure to store data, and its left and right child */
struct treeNode
{
int data;
struct treeNode* leftNode;
struct treeNode* rightNode;
// constructor to initialize data to the treeNode
treeNode (int data)
{
this->data = data;
leftNode = rightNode = NULL;
}
};
// funtion for iterative inorder traversal
void inOrderTraversal(struct treeNode *root)
{
stack<treeNode *> treeStack;
treeNode *currentNode = root;
while (currentNode != NULL || treeStack.empty() == false)
{
//condition to check if the node is leftmost node
while (currentNode != NULL)
{
// step 3 of our algorithm
treeStack.push(currentNode);
currentNode = currentNode->leftNode;
}
currentNode = treeStack.top();
treeStack.pop();
// cout statement to print the node data
cout << currentNode->data <<", ";
// statement to process right subtree
currentNode = currentNode->rightNode;
}
}
int main()
{ //code to create the binary tree
struct treeNode *root = new treeNode(1);
root->leftNode = new treeNode(2);
root->rightNode = new treeNode(3);
root->leftNode->leftNode = new treeNode(4);
root->leftNode->rightNode = new treeNode(5);
root->rightNode->rightNode = new treeNode(6);
inOrderTraversal(root); //function call
return 0;
}
Output:
4, 2, 5, 1, 3, 6,
Java program for iterative inorder traversal
import java.util.Stack;
/* binary tree node data structure to store data, and its left and right child */
class TreeNode
{
int data;
TreeNode leftNode;
TreeNode rightNode;
public TreeNode(int item)
{
data = item;
leftNode = rightNode = null;
}
}
/* Class to print the inorder traversal */
class BinaryTree
{
TreeNode root;
// funtion for iterative inorder traversal
void inOrderTraversal()
{
if (root == null)
return;
Stack<TreeNode> treeStack = new Stack<TreeNode>();
TreeNode currentNode = root;
while (currentNode != null || treeStack.size() > 0)
{
//condition to check if the node is leftmost node
while (currentNode != null)
{
/// step 3 of our algorithm
treeStack.push(currentNode);
currentNode = currentNode.leftNode;
}
currentNode = treeStack.pop();
// cout statement to print the node data.
System.out.print(currentNode.data + ", ");
// process right subtree now
currentNode = currentNode.rightNode;
}
}
public static void main(String args[])
{ //code to create the binary tree
BinaryTree tree = new BinaryTree();
tree.root = new TreeNode(1);
tree.root.leftNode = new TreeNode(2);
tree.root.rightNode = new TreeNode(3);
tree.root.leftNode.leftNode = new TreeNode(4);
tree.root.leftNode.rightNode = new TreeNode(5);
tree.root.rightNode.rightNode = new TreeNode(6);
tree.inOrderTraversal(); //function call
}
}
Output:
4, 2, 5, 1, 3, 6
Time complexity: O(n), where n is the number of nodes in the binary tree.
Space complexity: O(h), where h is the height of the binary tree, for a skewed tree this will be O(n).
Conclusion
- Traversing a tree means visiting each node of the tree.
- Inorder traversal means processing the left subtree, then the root, and then processing the right subtree.
- Iterative inorder traversal means doing inorder traversal without using recursion.
- Using stack data structure we can do the iterative inorder traversal.
- Inorder traversal uses the depth-first search technique.
- The time complexity for iterative inorder traversal is O(n), where n is the number of nodes in a binary tree.
- The space complexity for iterative inorder traversal is O(h), where h is the height of the binary tree.
- The iterative inorder traversal can be implemented with the help of data structures other than the stack, like queues, etc.