Problem Statement
Write a program that implements the operations of queue using an array
Implementation of Queue using Array Operations
The queue is the linear data structure that works on the principle of FIFO( First In First Out). In queue insertion and deletion of elements takes place at two different ends. The addition of an element happens at an end known as REAR and deletion happens at the FRONT end. Implementation of queue using array starts with the creation of an array of size n. And initialize two variables FRONT and REAR with-1which means currently queue is empty. The REAR value represents the index up to which value is stored in the queue and the FRONT value represents the index of the first element to be dequeued
Enqueue
Insert an element from the rear end into the queue. Element is inserted into the queue after checking the overflow condition n-1==REAR to check whether the queue is full or not.
- If n-1==REAR then this means the queue is already full.
- But if REAR<n means that we can store an element in an array.
- So increment the REAR value by 1 and then insert an element at the REAR index.
Dequeue
Deleting an element from the FRONT end of the queue. Before deleting an element we need to check the underflow conditionfront == – 1 or front > rear to check whether there is at least one element available for the deletion or not.
- If front == – 1 or front > rear then no element is available to delete.
- Else delete FRONT index element
- If REAR==FRONT then we set -1 to both FRONT AND REAR
- Else we increment FRONT.
Front
Returns the FRONT value of queue.
- First of all we need to check that queue is not empty.
- If the queue is empty then we display that the queue is empty we simply return from the function and not execute further inside the function
- Otherwise, we will return the FRONT index value.
Display
It will traverse the queue and print all the elements of the queue.
- Firstly check whether the queue is not empty.
- If empty we display that the queue is empty we simply return from the function and not execute further inside the function.
- Else we will print all elements from FRONT to REAR.
Example
Let us understand implementation of queue using array problem by an example n=5
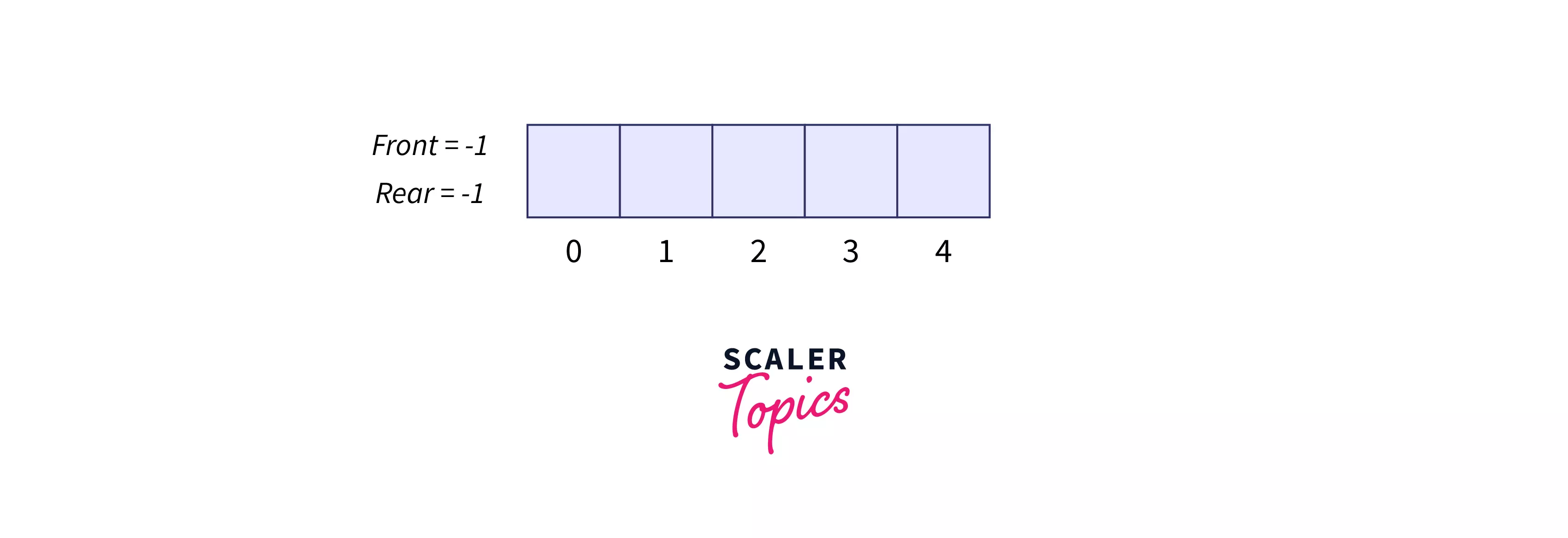
Refer to the below image to show an empty array creation of size 5
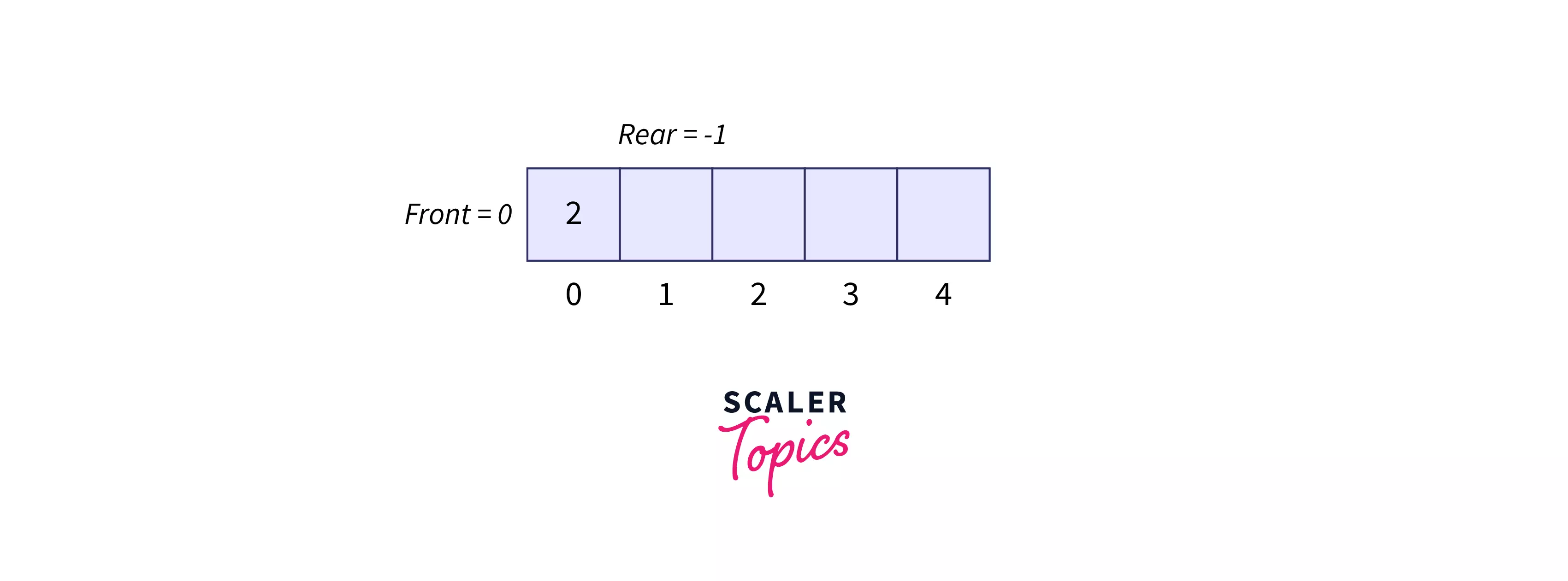
enqueue(2) Refer below image to show the enqueue operation
front()
2
enqueue(9) Refer below image to show the enqueue operation
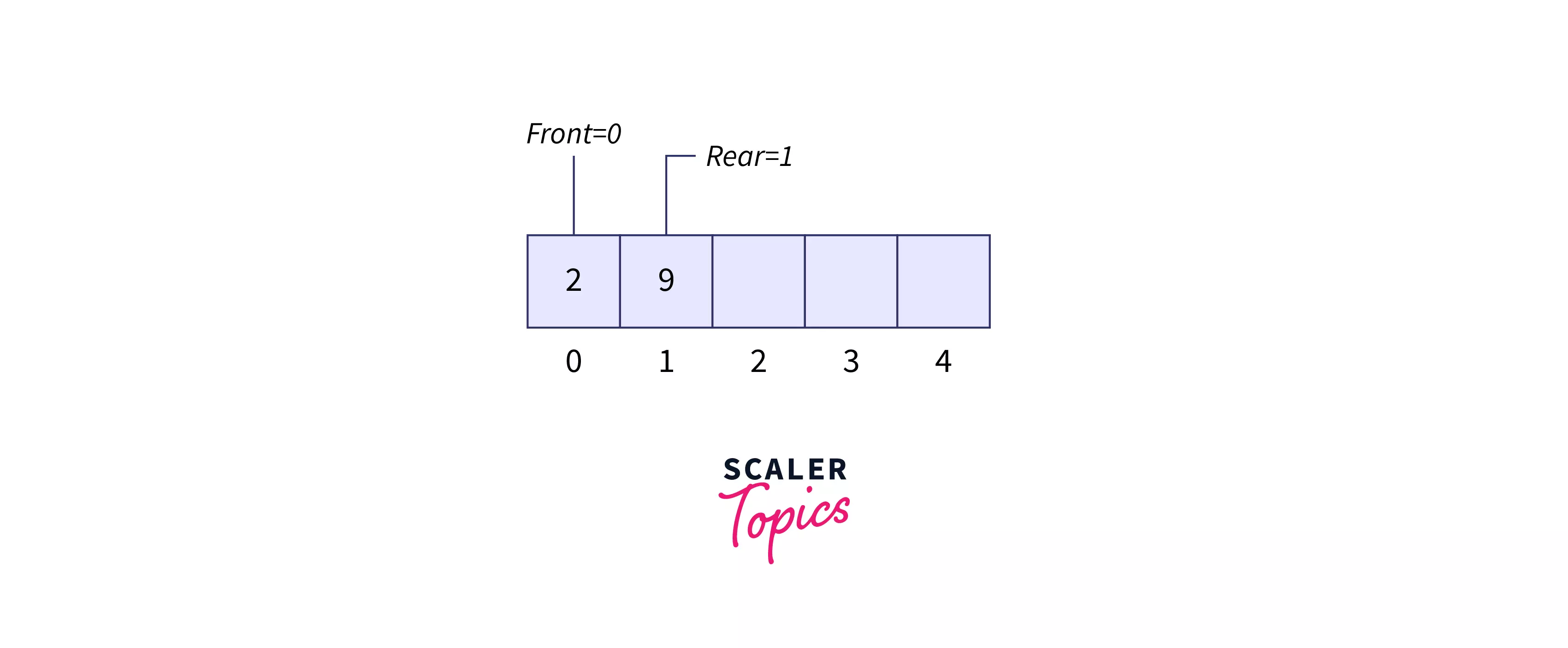
display()
2 9
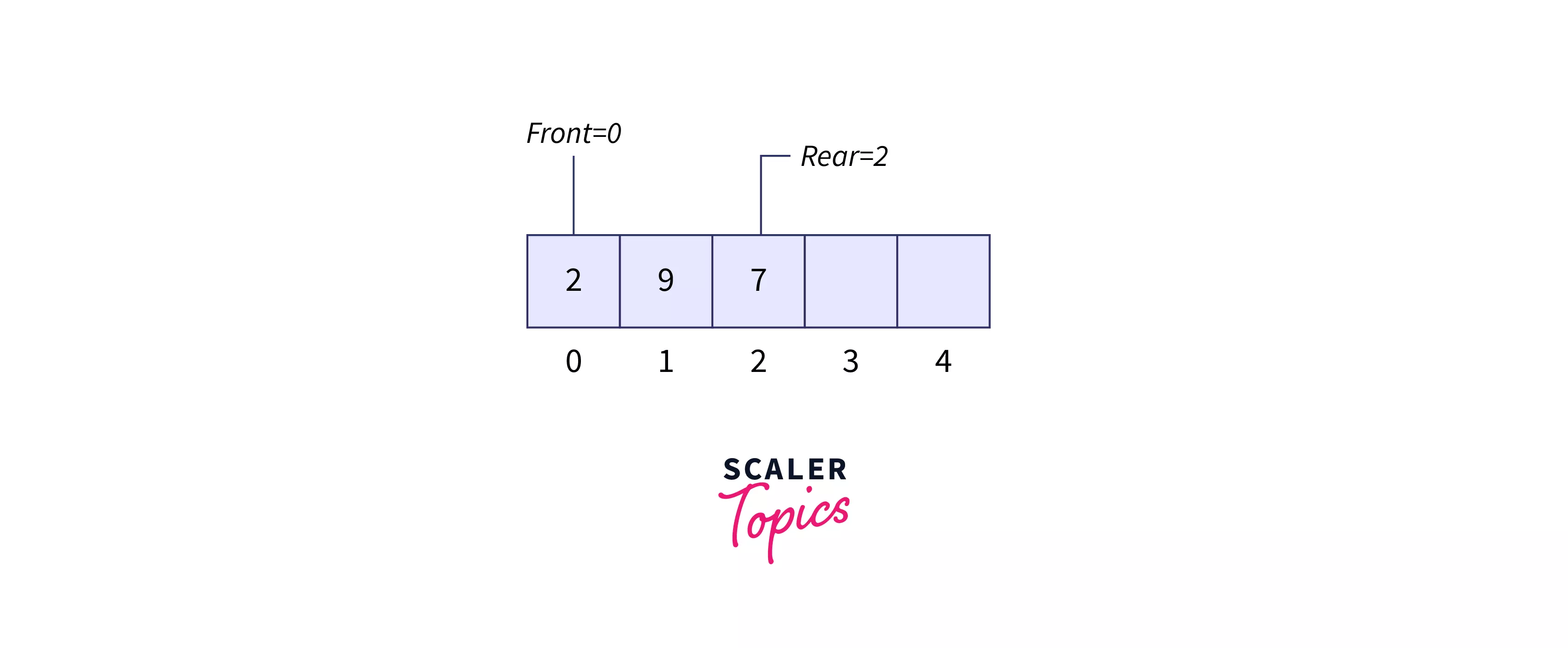
enqueue(7) Refer below image to show the enqueue operation
dequeue() Refer below image to show the dequeue operation
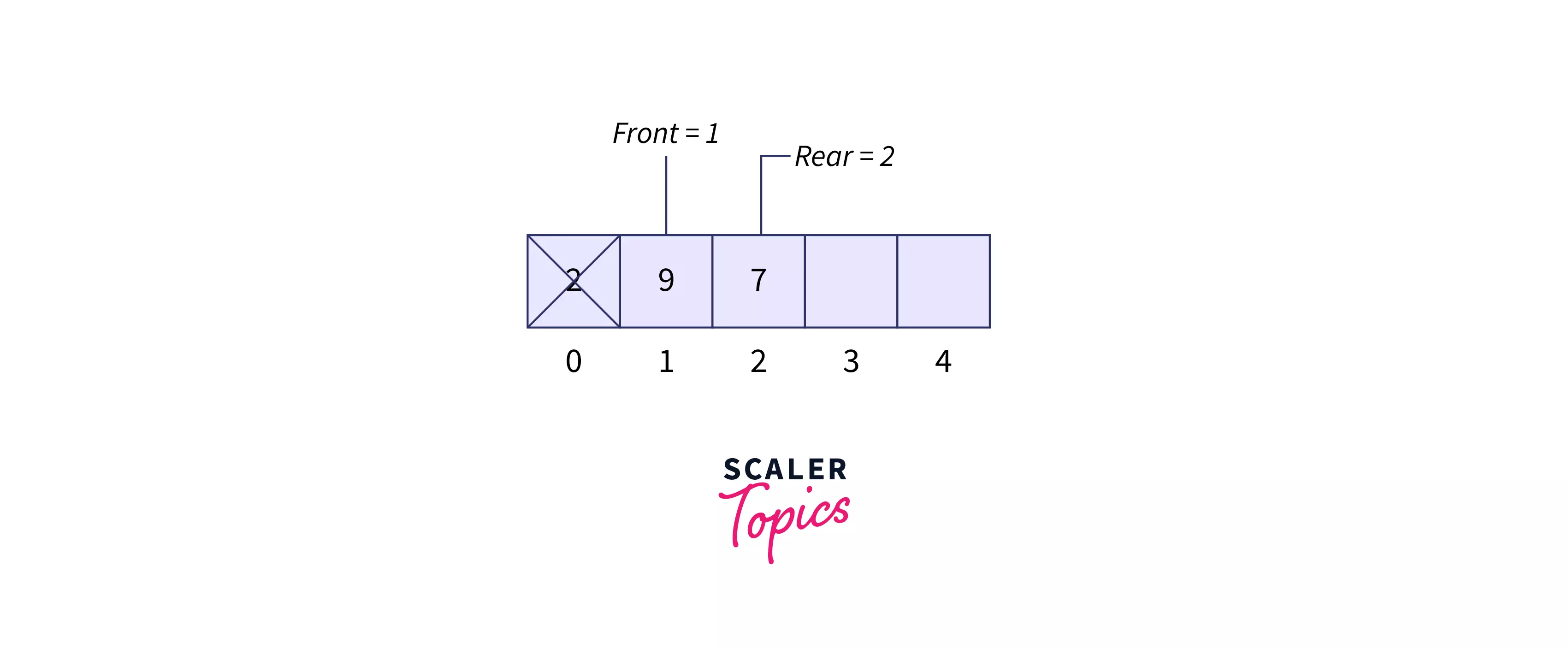
display()
9 7
enqueue(20) enqueue(30) Refer below image to show the enqueue operation
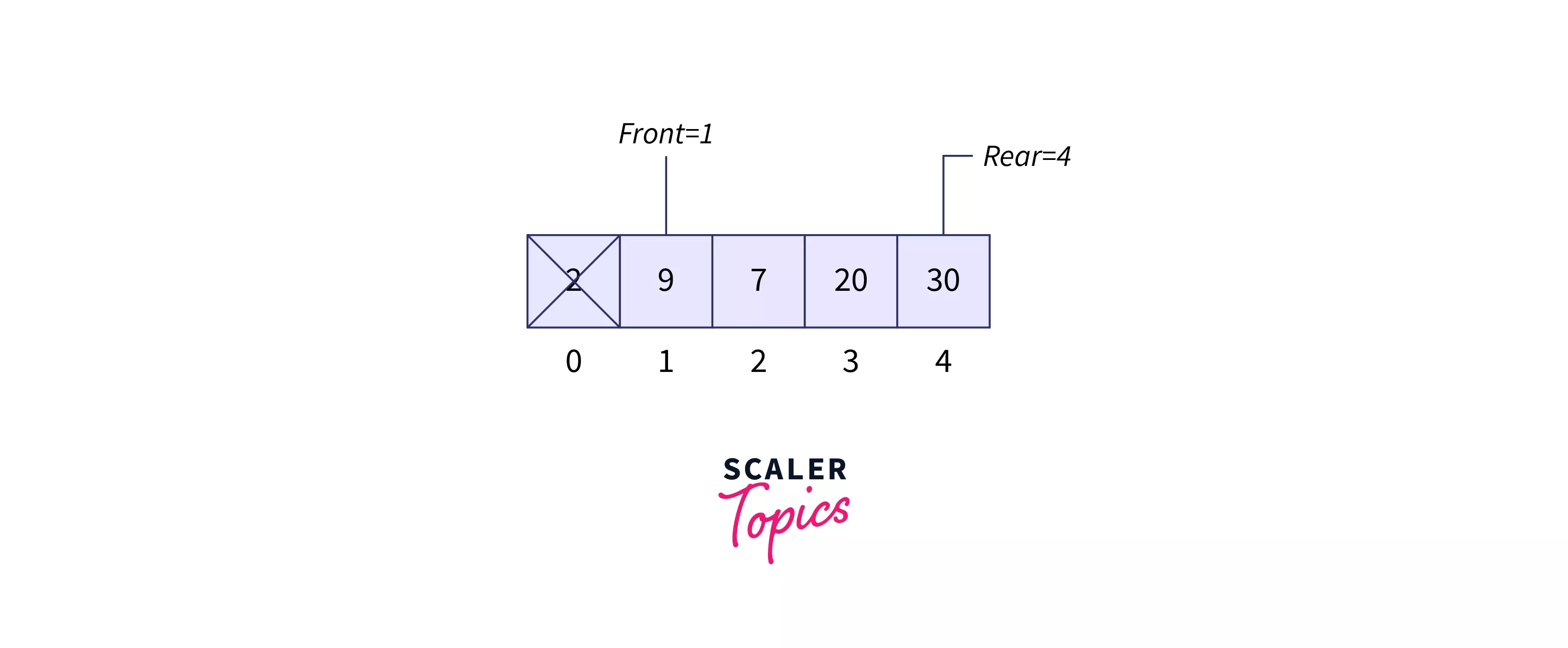
display()
9 7 20 30
dequeue() Refer below image to show the dequeue operation
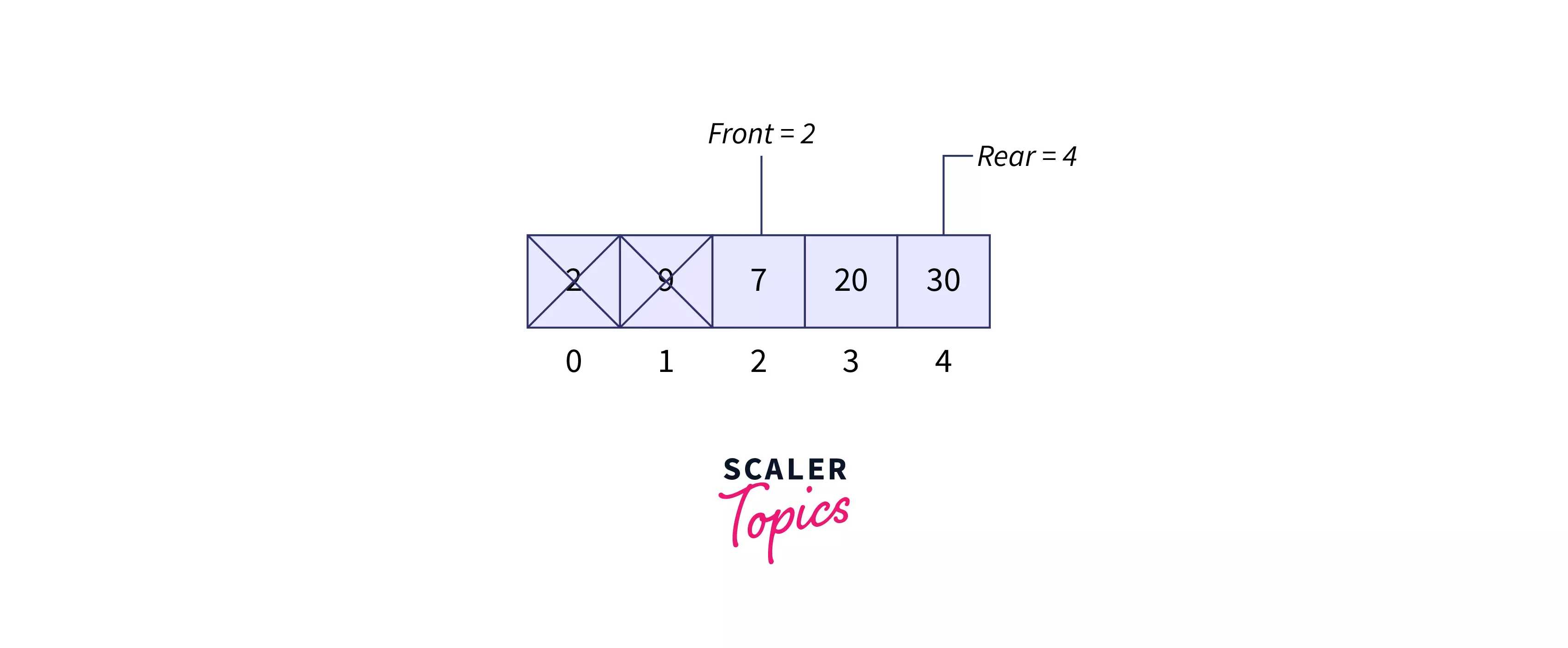
dequeue() Refer below image to show the dequeue operation
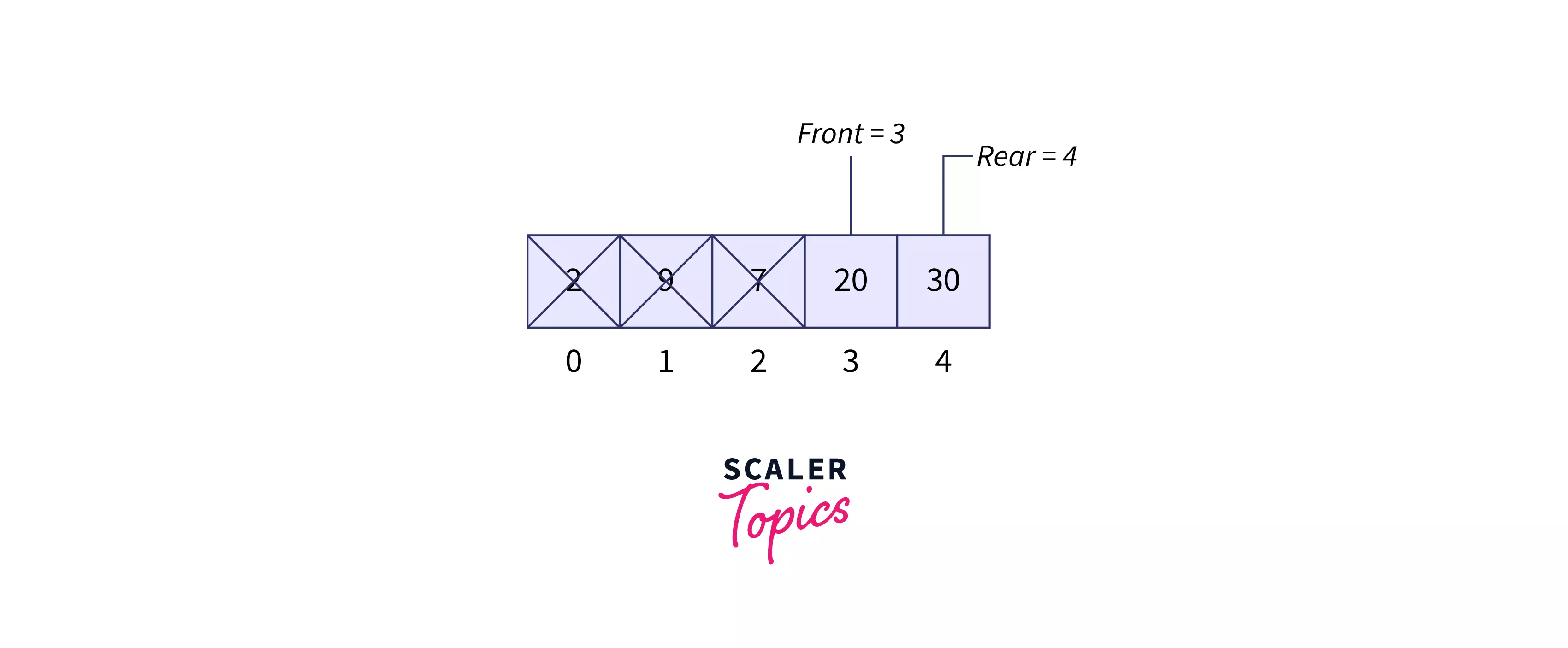
display()
20 30
Example Explanation
In the above example of implementation of queue using array problem, first of all we are creating an array named arr[] of size n which means the capacity of the queue is n and initializing FRONT and REAR as -1. Now for enqueue operation we increment REAR and insert an element at REAR arr[REAR]=item. For the dequeue operation, we delete an element at the FRONT index and increment FRONT by 1.
Input
The capacity of the queue is provided and queries are given as input to perform operations on the queue
Task
You need to perform all input operations of the queue with the help of an array.
Output
- enqueue() will print overflow if queue is already full otherwise it simply insert value * dequeue() will print underflow if queue is empty otherwise it will print deleted value. * display() will print all the elements of queue
- front() will print front element of queue if queue is not
Constraints
1 <= Size of the array <= 100
1 <= Number of queries <= 100
1 <= Element of the queue <= 100
Implementation of a Queue using Array
Algorithm
enqueue(item)
Step 1:
IF REAR = N - 1
Print “OVERFLOW! QUEUE IS ALREADY FULL”
TERMINATE
Step 2:
IF FRONT = -1 and REAR = -1
SET FRONT AND REAR AT 0 FRONT = REAR=0
ELSE
INCREMENT REAR BY 1 SET REAR = REAR + 1
[END OF IF]
Step 3:
INSERT ELEMENT AT REAR Set QUEUE[REAR] = ITEM
Step 4:
EXIT
dequeue()
Step 1:
IF FRONT = -1 or FRONT > REAR
Print “UNDERFLOW! QUEUE IS EMPTY”
TERMINATE
ELSE
SET DELETE FRONT VALUE VAL =QUEUE[FRONT]
Step 2:
IF FRONT==REAR
SET BOTH FRONT AND REAR AT -1 SET FRONT=REAR=-1
ELSE
INCREMENT FRONT BY 1 SET FRONT = FRONT + 1
[END OF IF]
Step 3:
EXIT
front()
Step 1:
IF FRONT = -1
Print “QUEUE IS EMPTY!”
ELSE
SET VAL = QUEUE[FRONT]
PRINT VAL
[END OF IF]
Step 2:
EXIT
display()
Step 1:
IF FRONT = -1
Print “QUEUE IS EMPTY!”
TERMINATE
ELSE
FOR ALL ITEM FROM FRONT TO REAR
PRINT ITEM
[END OF FOR]
[END OF IF]
Step 2:
EXIT
C++ Implementation C++ implementation of implementation of queue using array problem
// C++ program to implement queue using array
#include <iostream>
using namespace std;
// declaring the array of maximum capacity
int ar[10];
int n = 10;
// declaring front and rear and initializing both with -1
int front = - 1;
int rear = - 1;
//function to perform enqueue operation
void enqueue(int item) {
// checking overflow condition
if (rear == n - 1){
cout<<"Overflow!"<<endl;
return;
}
else {
// front and rear both are at -1 then
// set front and rear at 0 otherwise increment rear
if (front == - 1 && rear==-1){
front = 0;
rear=0;
}
else{
rear++;
}
//inserting element at rear
ar[rear] = item;
cout<<"Element inserted"<<endl;
}
}
//function to implement dequeue operation
void dequeue() {
//checking underflow condition
if (front == - 1 || front > rear) {
cout<<"Underflow!";
return ;
}
else {
int item=ar[front];
//displaying deleted element
cout<<"Element deleted from queue is : "<< item <<endl;
// if front and rear reach at end then initialize it at -1
if(front == rear) {
front = -1;
rear = -1;
}
else{
//incrementing the front
front++;
}
}
}
//function to display all elements of queue
void display() {
//checking whether queue is empty or not
if (front == - 1){
//if queue is empty simply return
cout<<"Queue is empty"<<endl;
return;
}
else {
// if queue is not empty print all the elements from rear to front
cout<<"Elements are : ";
for (int i = front; i <= rear; i++)
cout<<ar[i]<<" ";
cout<<endl;
}
}
//function to display front element of queue
void fronte() {
//checking whether queue is empty or not
if (front == - 1){
//if queue is empty simply return
cout<<"Queue is empty"<<endl;
return;
}
else {
// if queue is not empty print front element
cout<<"Front Element is :"<<ar[front]<<endl;
}
}
//driver code
int main() {
int ch;
//displaying options of enqueue, dequeue, front, display to the user
cout<<"1: Inserting element to queue(enqueue)"<<endl;
cout<<"2: Deleting element from queue(dequeue)"<<endl;
cout<<"3: Display front element of queue"<<endl;
cout<<"4: Display all the elements of queue"<<endl;
cout<<"5: Exit"<<endl;
do {
//taking user choice
cout<<"Enter your choice : "<<endl;
cin>>ch;
switch (ch) {
//calling functions according to the choice of user
case 1: {
cout<<"enter element to be inserted:"<<endl;
int item;
cin>>item;
enqueue(item);
break;
}
case 2: dequeue();
break;
case 3: display();
break;
case 4: fronte();
break;
case 5: cout<<"Exit"<<endl;
break;
default: cout<<"Invalid choice"<<endl;
}
} while(ch!=5);
return 0;
}
Java implementation Implementation of queue using array problem java implementation
// Java program to implement queue using array
import java.util.*;
class QueueUsingArray{
// declaring the array of maximum capacity
static int[] ar=new int[10];
static int n = 10;
// declaring front and rear and initializing both with -1
static int front = - 1;
static int rear = - 1;
//function to perform enqueue operation
static void enqueue(int item) {
// checking overflow condition
if (rear == n - 1){
System.out.println("Overflow!");
return;
}
else {
// front and rear both are at -1 then
// set front and rear at 0 otherwise increment rear
if (front == - 1 && rear==-1){
front = 0;
rear=0;
}
else{
rear++;
}
//inserting element at rear
ar[rear] = item;
System.out.println("Element inserted");
}
}
//function to implement dequeue operation
static void dequeue() {
//checking underflow condition
if (front == - 1 || front > rear) {
System.out.println("Underflow!");
return ;
}
else {
int item=ar[front];
//displaying deleted element
System.out.println("Element deleted from queue is : "+ item);
// if front and rear reach at end then initialize it at -1
if(front == rear) {
front = -1;
rear = -1 ;
}
else{
//incrementing the front
front++;
}
}
}
//function to display all elements of queue
static void display() {
//checking whether queue is empty or not
if (front == - 1){
//if queue is empty simply return
System.out.println("Queue is empty");
return;
}
else {
// if queue is not empty print all the elements from rear to front
System.out.println("Elements are : ");
for (int i = front; i <= rear; i++)
System.out.print(ar[i]+" ");
System.out.println();
}
}
//function to display front element of queue
static void fronte() {
//checking whether queue is empty or not
if (front == - 1){
//if queue is empty simply return
System.out.println("Queue is empty");
return;
}
else {
// if queue is not empty print front element
System.out.println("Front Element is :"+ar[front]);
}
}
//driver code
public static void main(String args[]) {
Scanner sc=new Scanner(System.in);
//displaying options of enqueue, dequeue, front, display to the user
System.out.println("1: Inserting element to queue(enqueue)");
System.out.println("2: Deleting element from queue(dequeue)");
System.out.println("3: Display front element of queue");
System.out.println("4: Display all the elements of queue");
System.out.println("5: Exit");
int ch;
do {
//taking user choice
System.out.println("Enter your choice : ");
ch=sc.nextInt();
switch (ch) {
//calling functions according to the choice of user
case 1: {
System.out.println("enter element to be inserted:");
int item=sc.nextInt();
enqueue(item);
break;
}
case 2: dequeue();
break;
case 3: display();
break;
case 4: fronte();
break;
case 5: System.out.println("Exit");
break;
default: System.out.println("Invalid choice");
}
}
while(ch!=5);
}
}
Python implementation Implementation of queue using array problem python implementation
# Python program to implement queue using array
# declaring the array of maximum capacity
ar = [0 for _ in range(10)]
n = 10
# declaring front and rear and initializing both with -1
front = - 1
rear = - 1
#function to perform enqueue operation
def enqueue(item):
# checking overflow condition
global n
global rear
global front
if rear == n - 1:
print("Overflow!", end = '')
print("\n", end = '')
return
else:
# front and rear both are at -1 then
# set front and rear at 0 otherwise increment rear
if front == - 1 and rear == -1:
front = 0
rear = 0
else:
rear += 1
#inserting element at rear
ar[rear] = item
print("Element inserted")
#function to implement dequeue operation
def dequeue():
global n
global rear
global front
#checking underflow condition
if front == - 1 or front > rear:
print("Underflow!", end = '')
return
else:
item = ar[front]
#displaying deleted element
print("Element deleted from queue is : ", end = '')
print(item, end = '')
print("\n", end = '')
#if front and rear reach at end then initialize it at -1
if rear == front:
rear = -1
front = -1
else:
front = front + 1
#incrementing the front
front += 1
#function to display all elements of queue
def display():
global n
global rear
global front
#checking whether queue is empty or not
if front == - 1:
#if queue is empty simply return
print("Queue is empty", end = '')
print("\n", end = '')
return
else:
# if queue is not empty print all the elements from rear to front
print("Elements are : ", end = '')
i = front
while i <= rear:
print(ar[i], end = '')
print(" ", end = '')
i += 1
print("\n", end = '')
#function to display front element of queue
def fronte():
global n
global rear
global front
#checking whether queue is empty or not
if front == - 1:
#if queue is empty simply return
print("Queue is empty", end = '')
print("\n", end = '')
return
else:
# if queue is not empty print front element
print("Front Element is :", end = '')
print(ar[front], end = '')
print("\n", end = '')
ch = None
#displaying options of enqueue, dequeue, front, display to the user
print("1: Inserting element to queue(enqueue)", end = '')
print("\n", end = '')
print("2: Deleting element from queue(dequeue)", end = '')
print("\n", end = '')
print("3: Display front element of queue", end = '')
print("\n", end = '')
print("4: Display all the elements of queue", end = '')
print("\n", end = '')
print("5: Exit", end = '')
print("\n", end = '')
condition = True
while condition:
#taking user choice
ch = int(input("Enter your choice:"))
#calling functions according to the choice of user
if ch == 1:
item = int(input("enter element to be inserted:"))
enqueue(item)
elif ch == 2:
dequeue()
elif ch == 3:
display()
elif ch == 4:
fronte()
elif ch == 5:
print("Exit", end = '')
print("\n", end = '')
else:
print("Invalid choice", end = '')
print("\n", end = '')
condition = ch!=5
Output:
1: Inserting element to queue(enqueue)
2: Deleting element from queue(dequeue)
3: Display front element of queue
4: Display all the elements of queue
5: Exit
Enter your choice:4
Queue is empty
Enter your choice:1
enter element to be inserted:4
Element inserted
Enter your choice:1
enter element to be inserted:5
Element inserted
Enter your choice:1
enter element to be inserted:2
Element inserted
Enter your choice:4
Front Element is :4
Enter your choice:3
Elements are : 4 5 2
Enter your choice:2
Element deleted from queue is : 4
Enter your choice:3
Elements are : 5 2
Enter your choice:1
enter element to be inserted:34
Element inserted
Enter your choice:4
Front Element is :5
Enter your choice:3
Elements are : 5 2 34
Enter your choice:5
Exit
Complexity
Time Complexity
enqueue(),dequeue(),front() can be perfromed in constant time. So time Complexity of enqueue, dequeue() , front() are O(1) but display will print all the elements of queue. So its time complexity is O(N). Overall worst case time complexity of implementation of queue using array is O(N).
Space Complexity
As we are using an array of size n to store all the elements of the queue so space complexity using array implemenation is O(N).
Drawbacks of Queue Implementation Using Array
Memory Wastage
In Implementation of queue using array there is a wastage of memory. The available free space in the array can not be used for storing elements.
Refer below image to show memory wastage problem
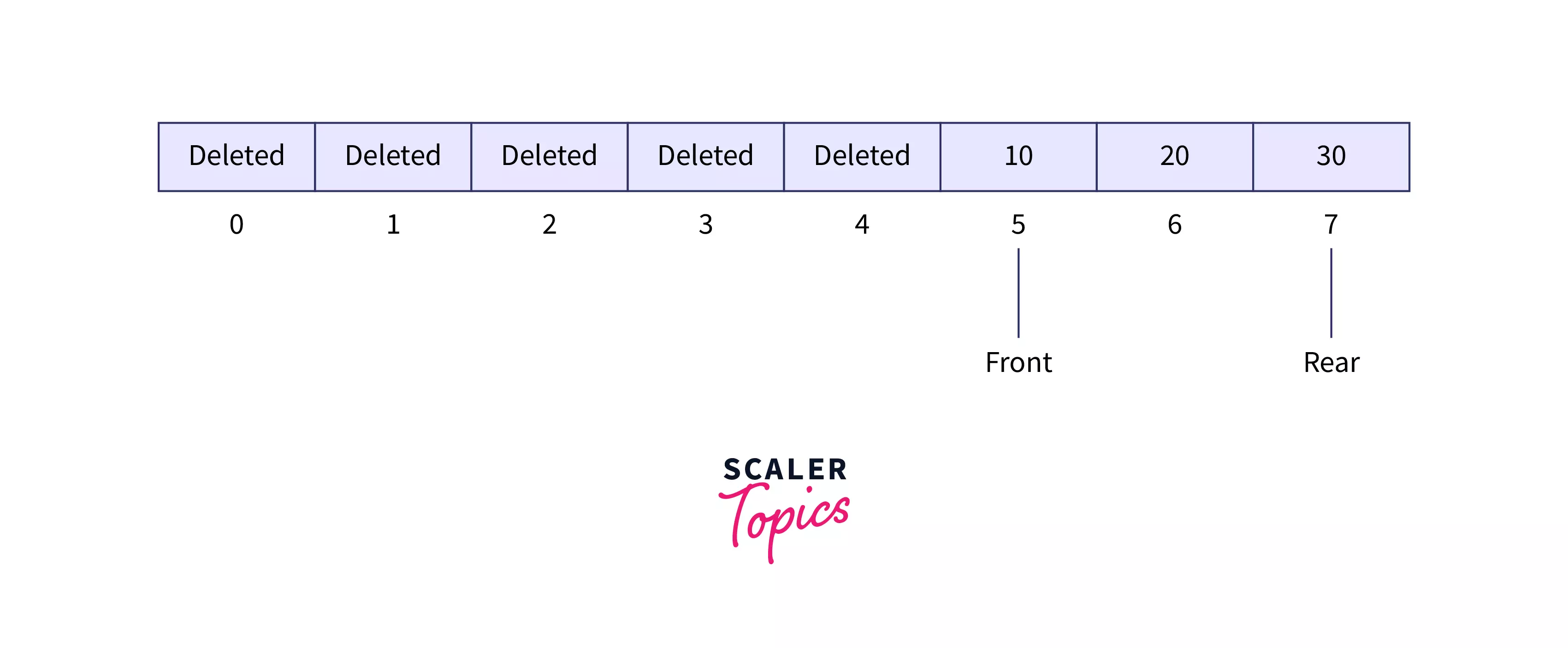
- In the above scenario free space is available in the array but when we try to insert element.
- Then REAR==N-1 condition becomes true so it will print overflow and insertion will not take place.
- So in array implementation we are not able to insert new elements even when the free space is available in the array.
Declaring the Array Size
- One of the common issue with array is that it requires static memory allocation, means we need to define array size at time of declaration of array.
- Change in size of array at the run time is very expensive process.
- So it is require to declare the array size in advance. Due to this, we declare a large size so that maximum possible queue elements are stored in array. But many slots of array may remain left unused which lead to wastage of memory.
- To overcome this, if we declare a small size array then it may become difficult to store all queue elements.
Conclusion
- Queue is a data structure that works on the principle of First In First Out(FIFO).
- Enqueue operation is performed to insert the element at the rear end of the queue.
- Dequeue operation is performed to delete elements from the front end of the queue.
- Display operation traverse the queue and print all its elements.
- Front will return the front element of the queue if the queue is not empty.
- There are some drawbacks of implementation of queue using array problem like memory wastage, and declaration of array size in advance.