Problem Statement
The problem statement here is to implement queue using stack.
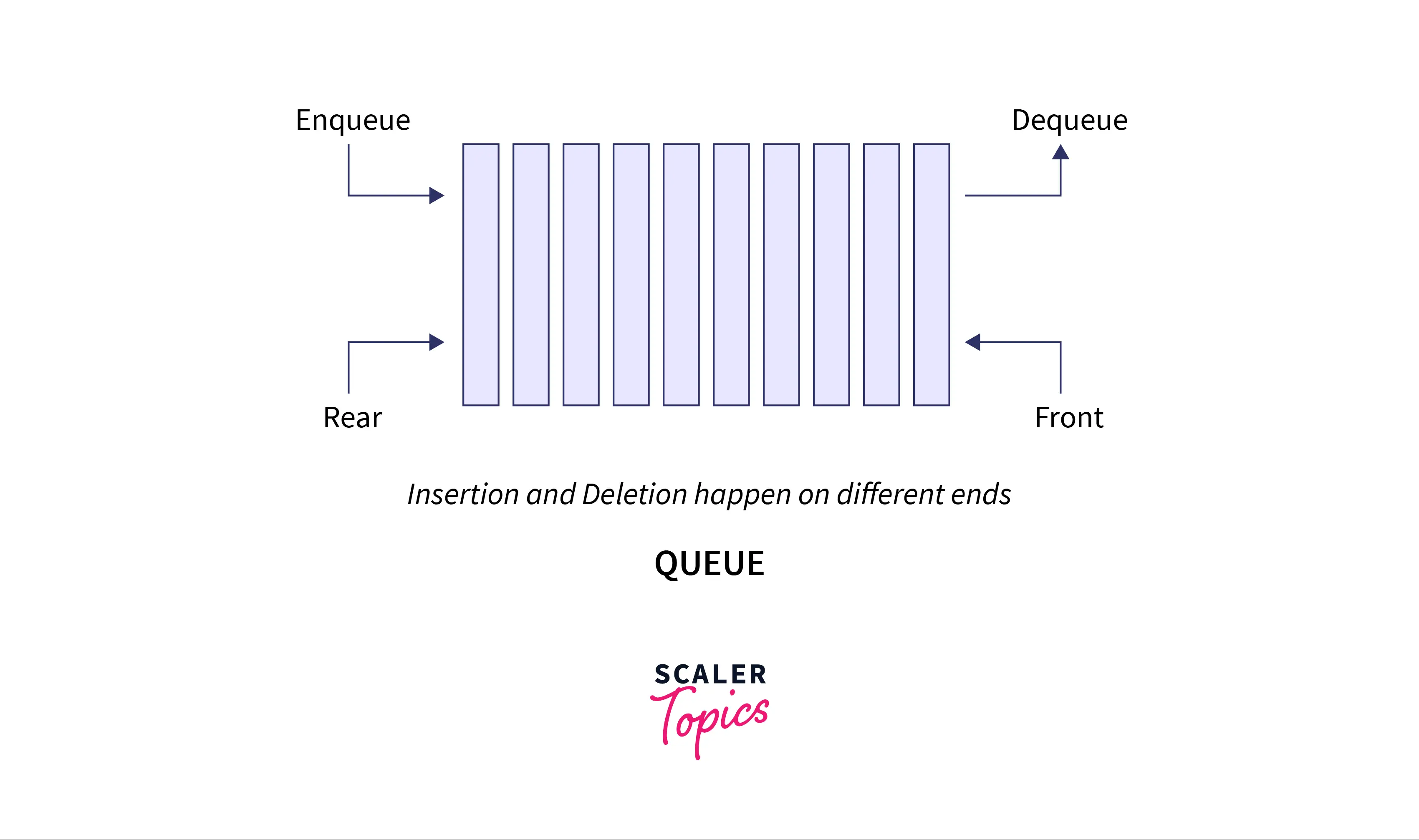
Queue is a linear data structure which follows First In First Out (FIFO) principle. This means that the element which is inserted first will be the one that will be removed first.
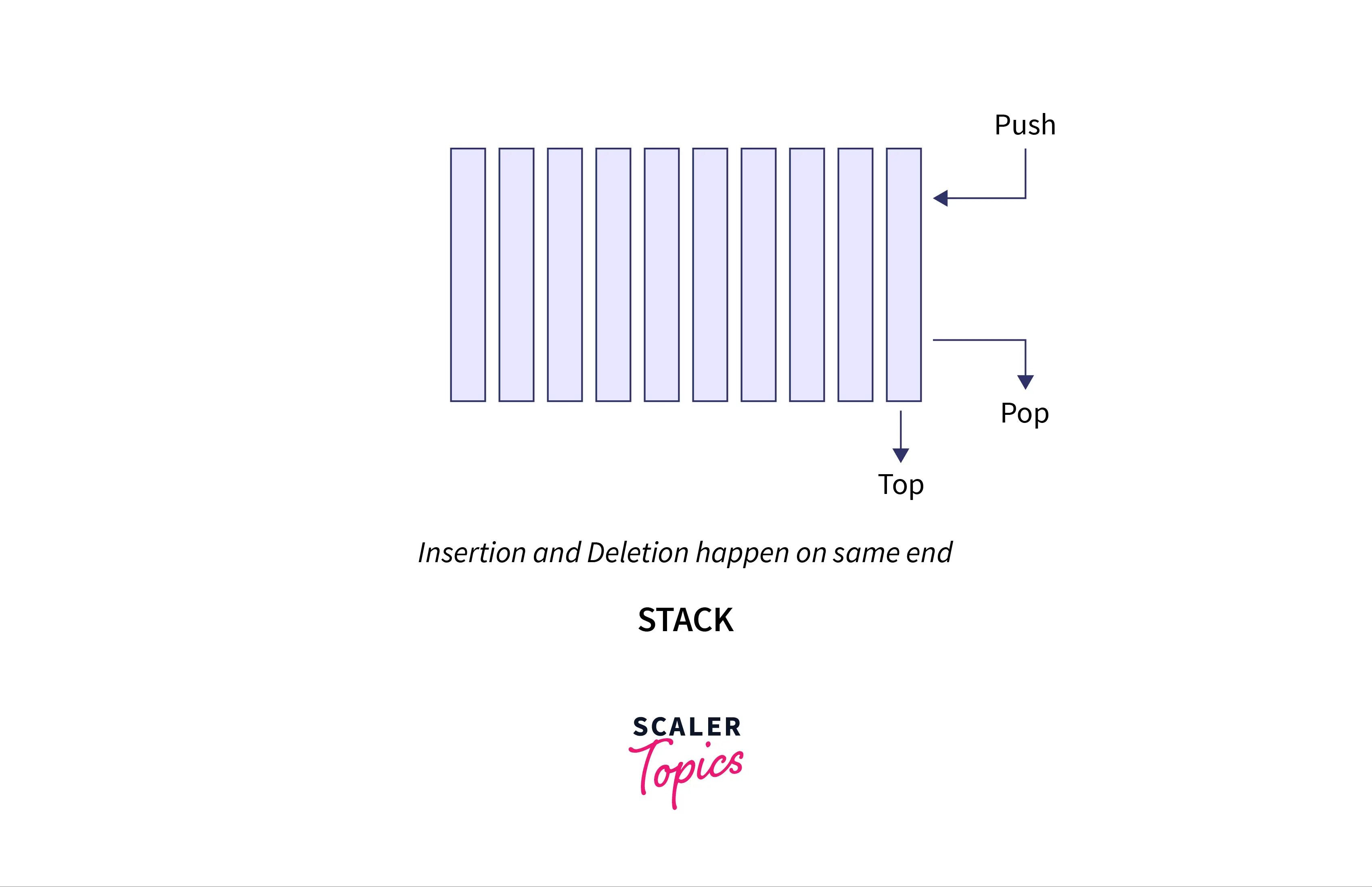
Stack is also a linear data structure which follows Last In First Out (LIFO) principle, means that the element inserted last in the stack will be the one to be removed first from the stack and vice versa.
By implementing queue using stack, we should be able to use the First In First Out functionality of the implmented queue with the help of push() and pop() functions. The implemented queue should be able to perform enqueue(insertion) and dequeue(removal) operations.
Example
Input:
queue = []
Operations = [ Push(1), Push(2), Push(3), Pop(), Pop() ]
Output:
For every operations queue will be upldated like: [ [1], [1, 2], [1, 2, 3], [2, 3], [3] ]
Explanation: The queue is using stack operations to implement FIFO functionality, so till the data is pushed to the queue, it will be [1, 2, 3] and for the first Pop() function the firstly entered element will be removed from the queue, so the queue will be [2, 3].
Now for the next Pop() operation, the element 2 will be removed from the queue as it is the most oldest element in the queue, now the queue is [3].
Constraints
$1 <= queue.length <= 1000$
$0 <= queue[i] <= 1000$
Approach 1: Making a dequeue operation costly
As we know that a queue follows FIFO functionality, so to implement queue using stack, we will have to make it in a way that the element entering first in the queue will be the first to be removed.
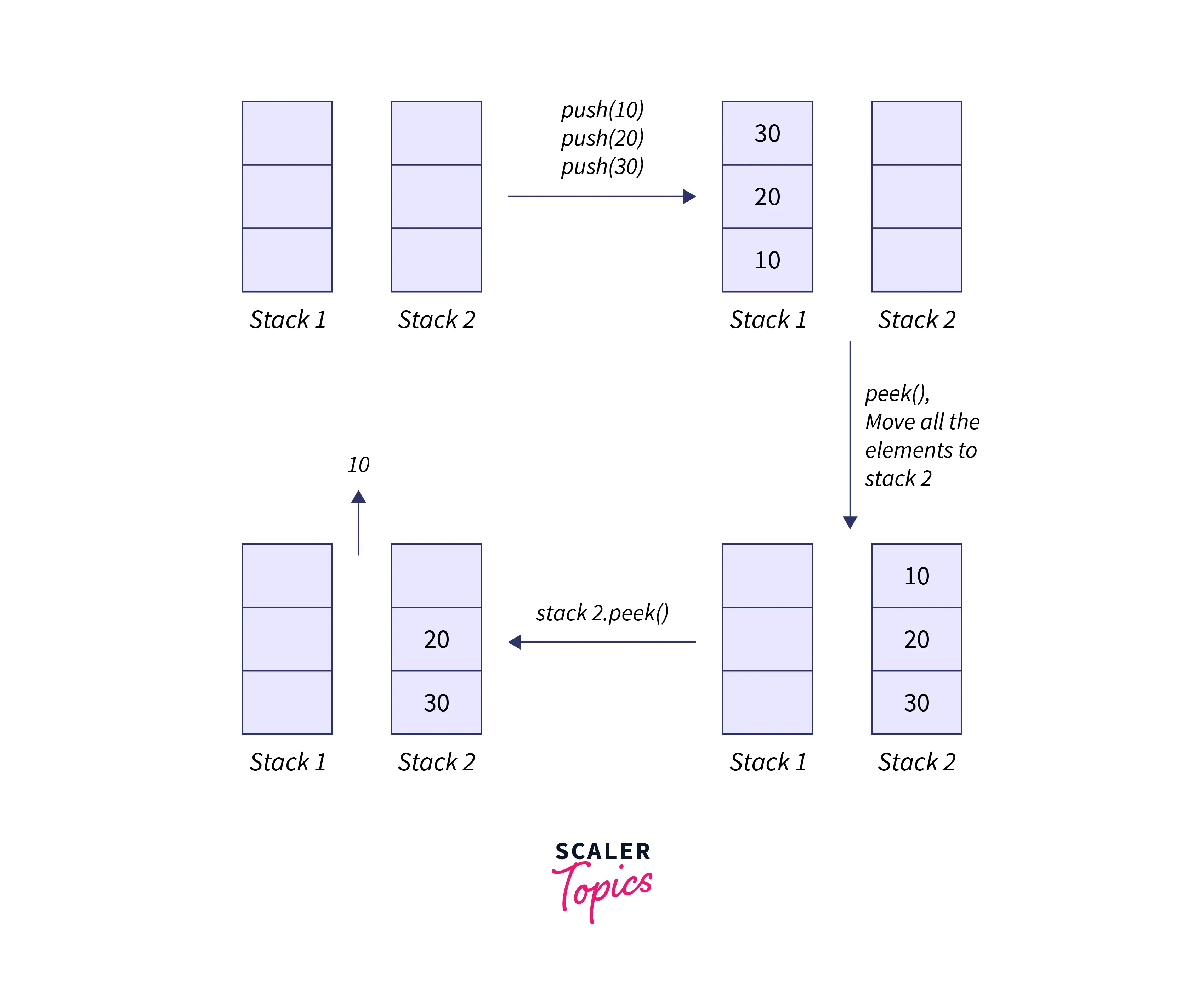
This can be done by using two stacks. By using 2 stacks at a time, we can simply push the element in stack 1 and will pop the first occuring element by pushing all the elements of stack 1 to stack 2 and popping out the top element of stack 2.
In this approach to implement queue using stack, we are making the dequeue operation of one stack costly for reaching the functionality of a queue.
Algorithm: We can implement queue using stack using the below algorithm
Initialize 2 empty stacks s1 and s2
- For enqueue operation
- push the element to the top of the stack
s1.
- push the element to the top of the stack
- For deque operation
- if
s1ands2is empty, return-1as the is no element to remove. - If
s2is empty, push all the elements of stack froms1tos2. - remove the top element of the stack
s2.
- if
Complexity Analysis
Time Complexity:
- push operation: O(1)
It is same as the push operation in the stack. - pop operation: O(N).
In the worst case we have empty whole ofstack 1intostack 2.
Space Complexity: O(N) => N space for storing N elements in the stacks.
C++ Implementation
struct Queue {
// Initializing the stacks
stack<int> stack1, stack2;
// Function to implement enqueue
void enqueue(int element)
{
// Pushing element in the stack
stack1.push(element);
}
// Function to implement dequeue operation
int dequeue()
{
// Condition where the queue is empty
if (stack1.empty() && stack2.empty()) {
cout << "the queue is empty";
exit(0);
}
// Pushing all the elements of stack1 to stack2
if (stack2.empty()) {
while (!stack1.empty()) {
stack2.push(stack1.top());
stack1.pop();
}
}
// Popping the top element from the stack
int element = stack2.top();
stack2.pop();
return element;
}
};
Java Implementation
static class Queue {
// Initializing the stacks
Stack<Integer> stack1;
Stack<Integer> stack2;
}
// Function to implement enqueue
static void enqueue(Queue q, int element)
{
// Pushing element in the stack
push(q.stack1, element);
}
// Function to implement dequeue operation
static int dequeue(Queue q)
{
int element;
// Condition where the queue is empty
if (q.stack1.isEmpty() && q.stack2.isEmpty()) {
System.out.println("the queue is empty");
System.exit(0);
}
// Pushing all the elements of stack1 to stack2
if (q.stack2.isEmpty()) {
while (!q.stack1.isEmpty()) {
element = q.stack1.pop();
q.stack2.push(element);
}
}
// Popping the top element from the stack
element = q.stack2.pop();
return element;
}
Python Implementation
class Queue:
def __init__(self):
# Initializing the stacks
self.s1 = []
self.s2 = []
# Function to implement enqueue
def enqueue(self, element):
# Pushing element in the stack
self.s1.append(element)
# Function to implement dequeue operation
def dequeue(self):
# Condition where the queue is empty
if (len(self.s1) == 0 and len(self.s2) == 0):
print("the queue is Empty")
return
elif (len(self.s2) == 0 and len(self.s1) > 0):
while len(self.s1):
element = self.s1.pop()
self.s2.append(element)
return self.s2.pop()
else:
# Popping the top element from the stack
return self.s2.pop()
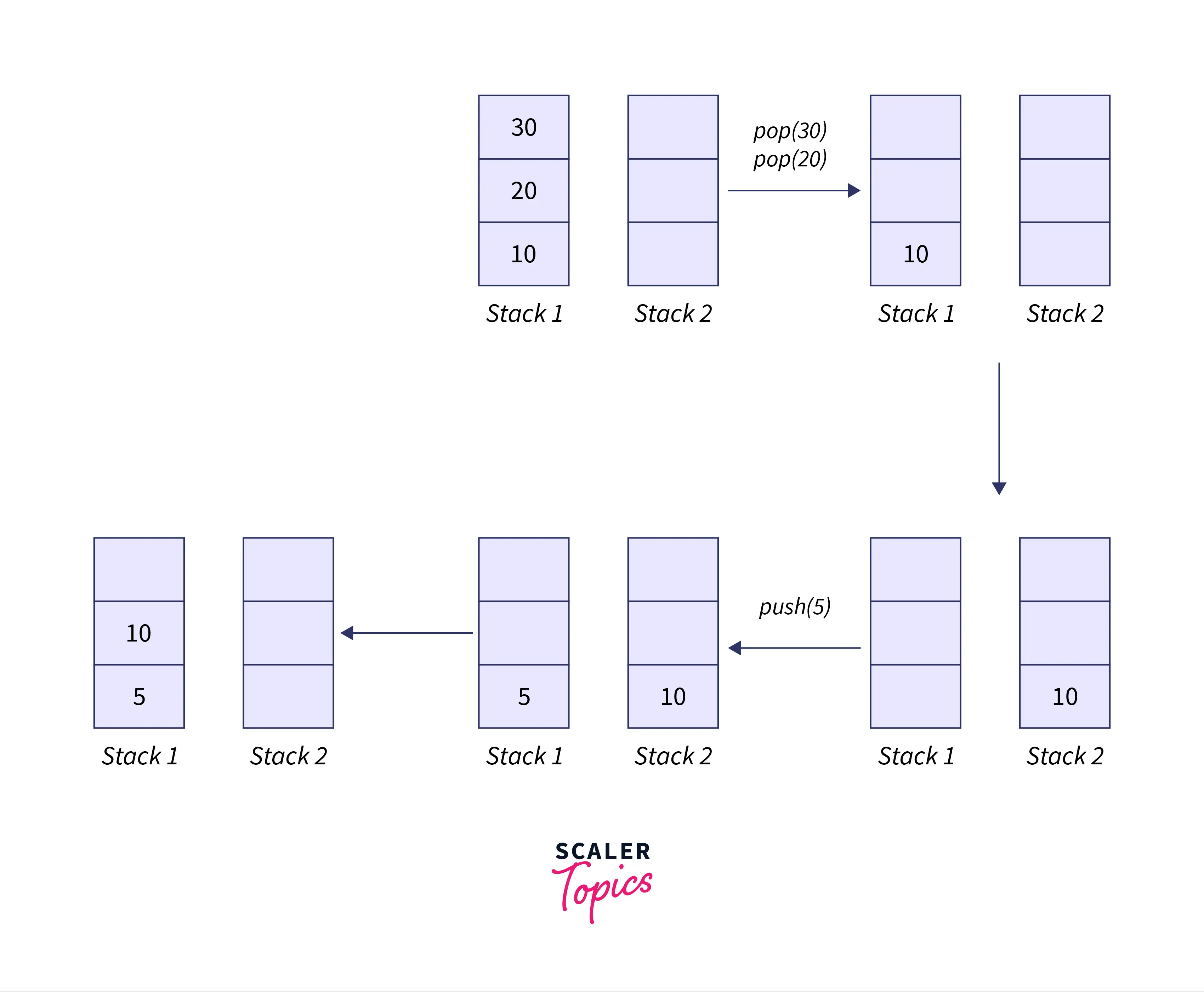
Approach 2: Making a enqueue operation costly
In this approach to implement queue using stack, we are making use of 2 stacks for the opertions by making the enqueue operation of one stack costly for reaching the functionality of a queue.
Algorithm: We can implement queue using stack using the below algorithm
Initialize 2 empty stacks s1 and s2
- For enqueue operation
- while the stack s1 is empty, push the element to stack s2.
- else, push all the elements from stack s1 to stack s2, and push the element to the top of the stack s1.
- Now, Push all the elements from stack s2 to stack s1.
- For deque operation
- if the stack is empty, return -1.
- Otherwise, pop and return the top element of the stack s1.
Complexity Analysis
Time Complexity:
- push operation: O(N) In the worst case we have empty whole of stack 1 into stack 2 and vice versa.
- pop operation: O(1). It is same as the pop operation in the stack.
Space Complexity: O(N) => N space for storing N elements in the stacks.
C++ Implementation
struct Queue {
// Initializing both the stacks
stack<int> stack1, stack2;
// Function to implement enqeue operation
void enqueue(int element)
{
// Push all the elements of stack1 to stack2
while (!stack1.empty()) {
stack2.push(stack1.top());
stack1.pop();
}
stack1.push(element);
// Push all the elements back to s1
while (!stack2.empty()) {
stack1.push(stack2.top());
stack2.pop();
}
}
// Function to implement deqeue operation
int dequeue()
{
// If stack1 is empty, return -1 or a message
if (stack1.empty()) {
cout << "the queue is Empty";
exit(0);
}
// Top of the stack is returned
int element = stack1.top();
stack1.pop();
return element;
}
};
Java Implementation
static class Queue
{
// Initializing both the stacks
static Stack<Integer> stack1 = new Stack<Integer>();
static Stack<Integer> stack2 = new Stack<Integer>();
// Function to implement enqeue operation
static void enqueue(int element)
{
// Push all the elements of stack1 to stack2
while (!stack1.isEmpty())
{
stack2.push(stack1.pop());
}
stack1.push(element);
// Push all the elements back to s1
while (!stack2.isEmpty())
{
stack1.push(stack2.pop());
//s2.pop();
}
}
// Push all the elements back to s1
static int dequeue()
{
// If stack1 is empty, return -1 or a message
if (stack1.isEmpty())
{
System.out.println("the queue is Empty");
System.exit(0);
}
// Top of the stack is returned
int element = stack1.peek();
stack1.pop();
return element;
}
Python Implementation
class Queue:
def __init__(self):
# Initializing both the stacks
self.stack1 = []
self.stack2 = []
# Function to implement enqeue operation
def enqueue(self, element):
# Push all the elements of stack1 to stack2
while len(self.stack1) != 0:
self.stack2.append(self.stack1[-1])
self.stack1.pop()
self.stack1.append(element)
# Push everything back from stack2 to stack1
while len(self.stack2) != 0:
self.stack1.append(self.stack2[-1])
self.stack2.pop()
# Function to implement deqeue operation
def dequeue(self):
# If stack1 is empty, return -1 or a message
if len(self.stack1) == 0:
print("the queue is Empty")
# Top of the stack is returned
element = self.stack1[-1]
self.stack1.pop()
return element
Conclusion
- The problem statement here is to implement queue using stack.
- implement queue using stack means we should be able to use the First In First Out functionality of the implmented queue.
- There are two techniques to implement queue using stack:
- Making a dequeue operation costly: the dequeue operation will take O(N) time and enqueue will be time effective with the time complexity of O(1).
- Making an enqueue operation costly: The enqueue operation will take O(N) time and dequeue will be time effective with the time complexity of O(1).