When you want to send files or store the files on a computer, if the size is very huge we generally compress it and store it.
One way of compressing these files is using Huffman Coding which is a greedy-based algorithm that is also known as variable-length coding or lossless data compression technique.
Introduction to Huffman Coding
Huffman Coding is a technique that is used for compressing data to reduce its size without losing any of its details. It was first developed by David Huffman and was named after him.
Huffman Coding is generally used to compress the data which consists of the frequently repeating characters.
Huffman Coding is a famous Greedy algorithm. It is said to be a Greedy Algorithm because the size of code assigned to a character depends on the frequency of the character.
The character with higher frequency gets the short-length variable code and vice-versa for characters with lower frequency. It uses a variable-length encoding which means that it assigns a variable-length code to all the characters in the given stream of data.
Prefix Rule
This rule basically means that the code which is assigned to any character should not be the prefix of any other code.
If this rule is not followed, then some ambiguities can occur during the decoding of the Huffman tree formed.
To understand more about this rule let’s consider an example: For example, code is given for each character:
a - 0
b - 1
c - 01
Now assume that the generated bitstream is 001, while decoding the code it can be written as follows:
0 0 1 = aab
0 01 = ac
This means that the given string can be aab or else ac, such ambiguities can be avoided if we follow the prefix rule. Since no codeword is a prefix of any other, the codeword that starts with encoded data is unambiguous.
How does Huffman Coding work?
There are mainly two major steps involved in obtaining the Huffman Code for each unique character:
- Firstly, build a Huffman Tree from the given stream of data(only taking the unique characters).
- Secondly, we need to traverse the Huffman Tree which is formed and assign codes to characters and decode the given string using these huffman codes.
Major Steps in Huffman Coding
Steps involved in building the Huffman tree from the given set of characters
Input:
string str = "abbcdbccdaabbeeebeab"
Here, if Huffman Coding is used for data compression, then we need to determine the following for decoding:
- Huffman Code for each character
- Average code length
- Length of Huffman encoded message (in bits)
The last two of them are found using formulas that are discussed below.
How to Build a Huffman Tree from Input Characters?
- Firstly, we need to calculate the frequency of each character in the given string.
| Character | Frequency/count |
|---|---|
| a | 4 |
| b | 7 |
| c | 3 |
| d | 2 |
| e | 4 |
- Sort the characters in ascending order of frequency. These are stored in a priority queue Q/ min-heap.
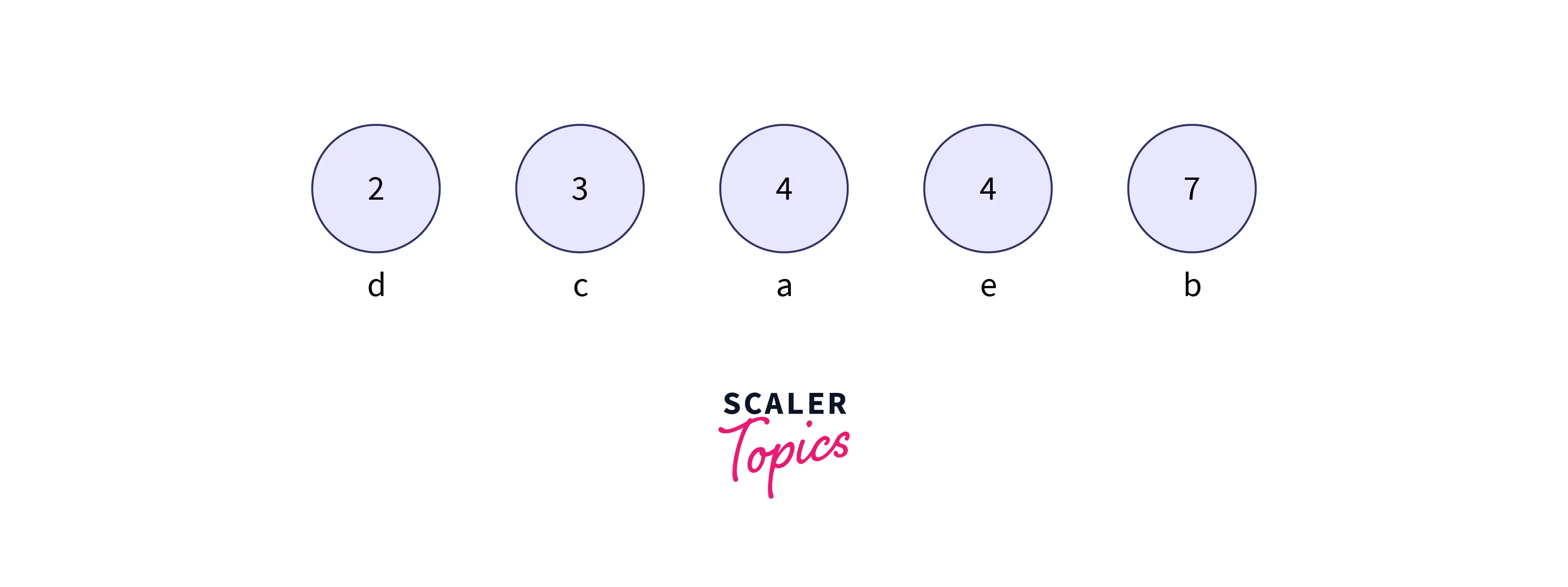
- Create a leaf node for every unique character and its frequency from the given stream of data.
- Extract the two minimum frequency nodes from the nodes and the sum of these frequencies is made the new root of the tree.
- While extracting the nodes with the minimum frequency from the min-heap:
- Make the first extracted node its left child and the other extracted node as its right child.
- Add this node to the min-heap.
- Since the minimum frequency should always be on the left side of the root.
- Repeat steps 3 and 4 until the heap contains only one node(i.e, all characters are included in the tree). The remaining node is the root node and the tree is complete.
Example of Huffman Coding
Let us understand the algorithm with an example:
Huffman Coding Algorithm
Step 1: Build a min-heap that contains 5 (number of unique characters from the given stream of data) nodes where each node represents the root of a tree with a single node.
Step 2: Get two minimum frequency nodes from the min heap. Also, add a new internal node formed by combining the two nodes which are extracted, frequency 2 + 3 = 5.
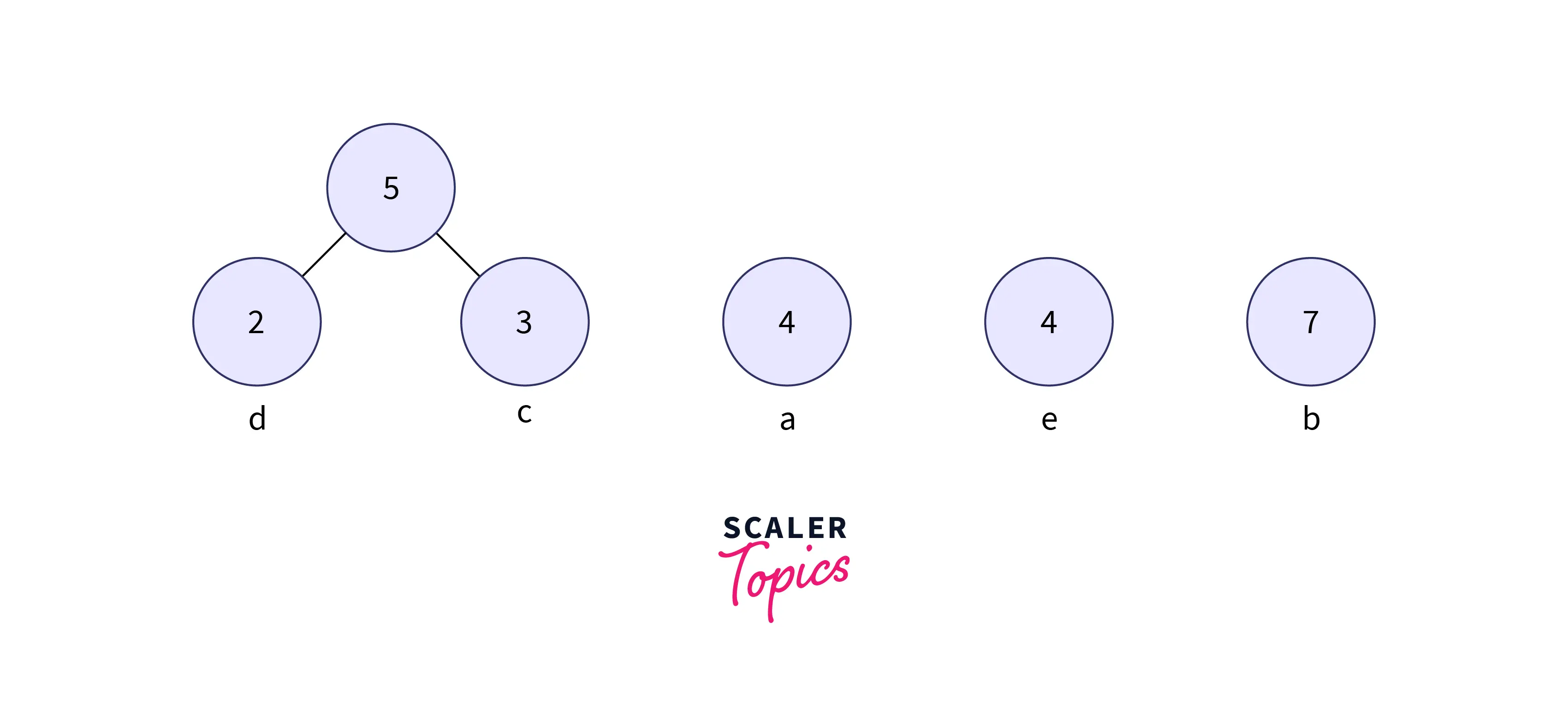
- Now min-heap contains 4 nodes where 3 nodes are roots of trees with a single element each, and one heap node is the root of the tree with 2 elements
Step 3: Similarly, get the two minimum frequency nodes from the heap. Also add a new internal node formed by combining the two nodes which are extracted, the frequency to be added in the tree is 4 + 4 = 8
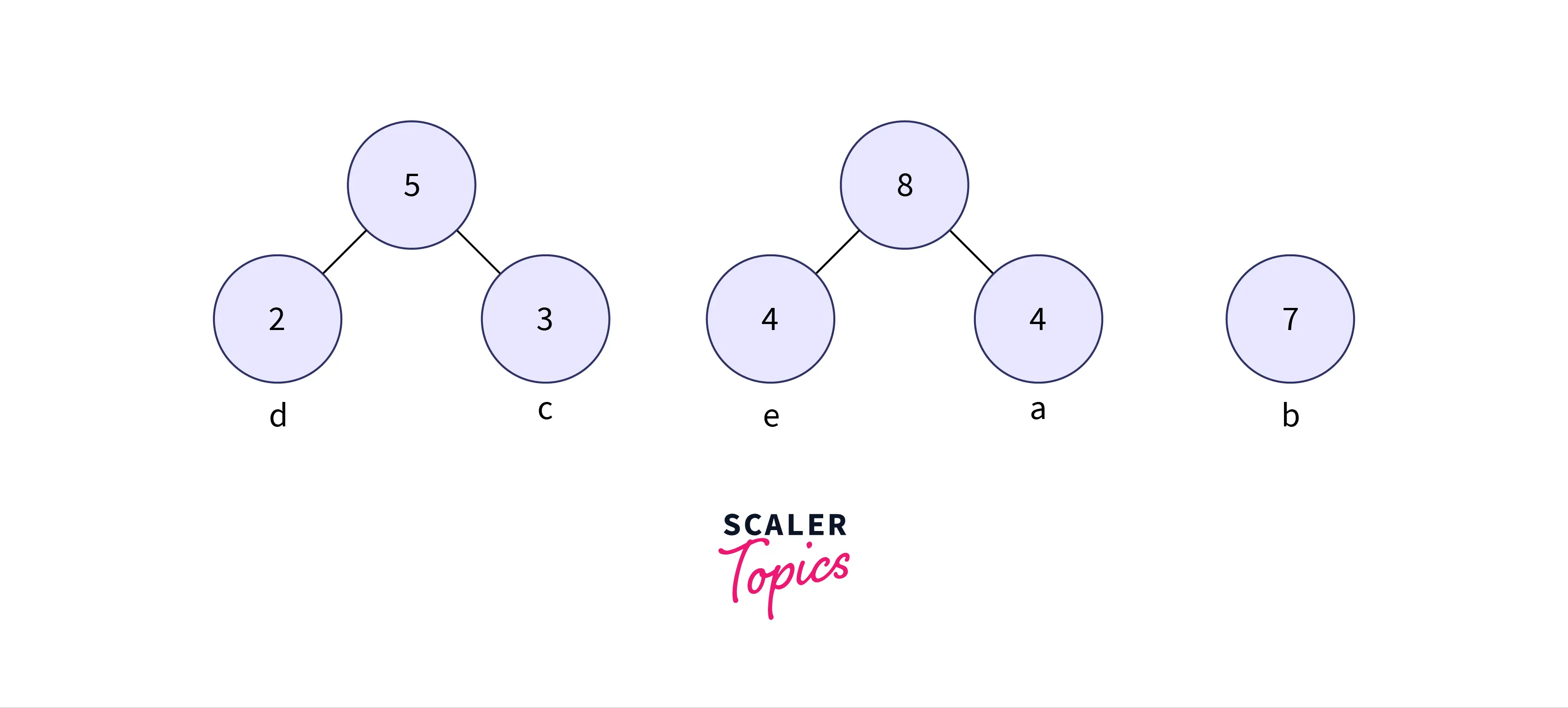
- Now min heap contains 3 nodes where 1 node is the root of trees with a single element, and two heap nodes are the root of the tree with more than one node.
Step 4: Get the two minimum frequency nodes. Also add a new internal node formed by combining the two nodes which are extracted, frequency to be added in the tree is 5 + 7 = 12.
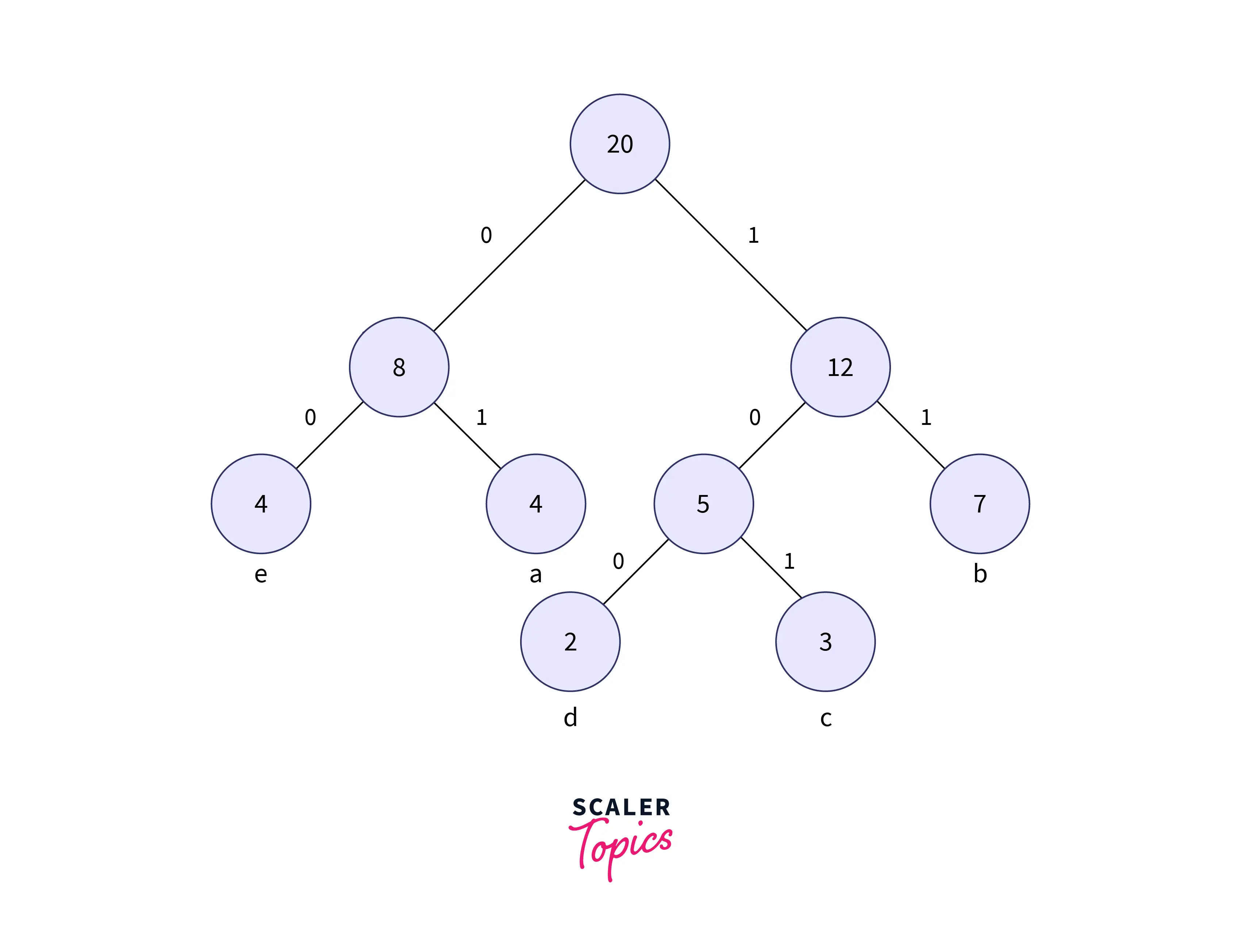
- When designing a Huffman tree, we need to check that the minimum value is placed on the left side of the tree always and the second one should be on the right side of the tree. Now the tree formed is shown in the below image:
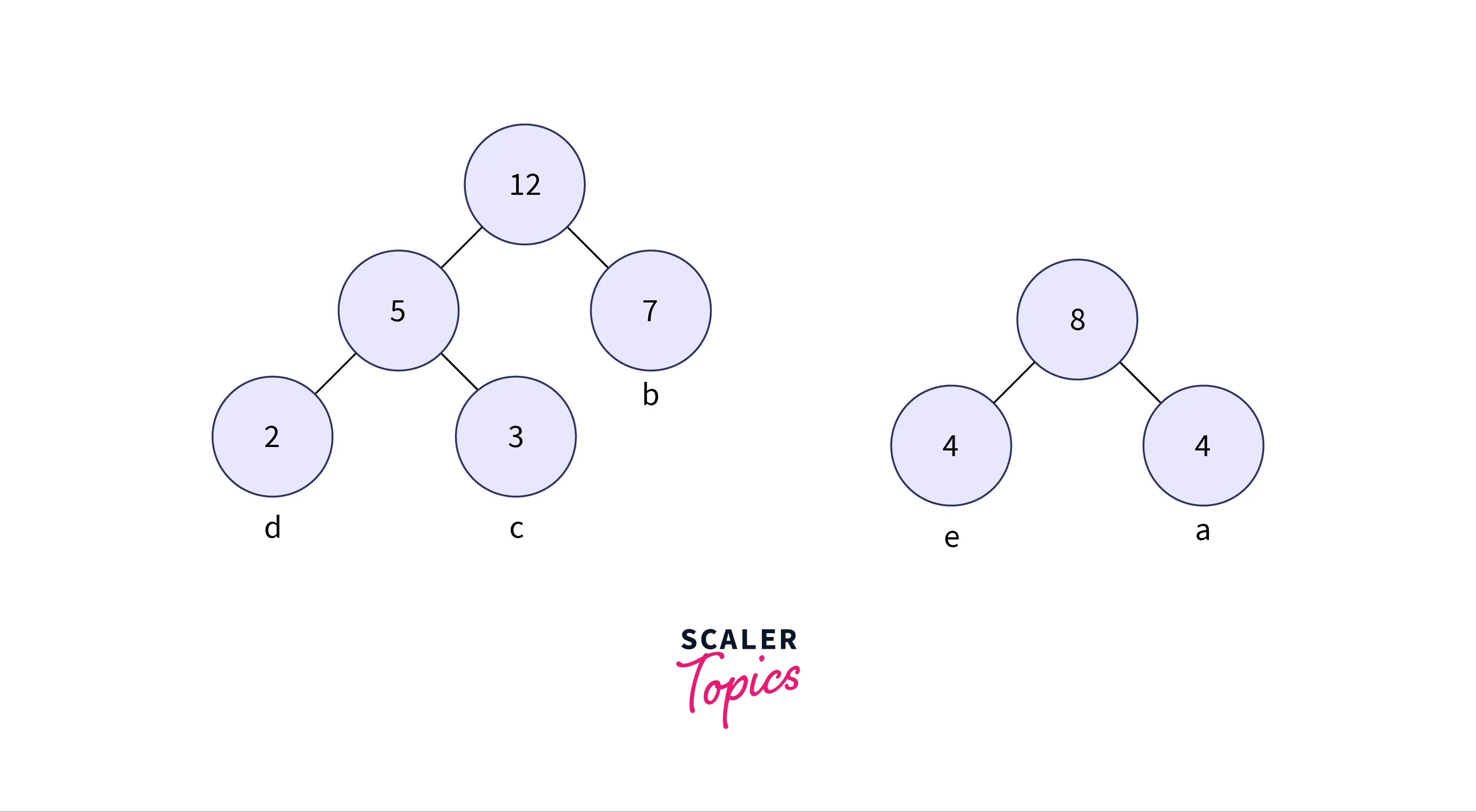
Step 5: Get the next two minimum frequency nodes. Also, add a new internal node formed by combining the two nodes which are extracted, the frequency to be added in the tree is 12 + 8 = 20
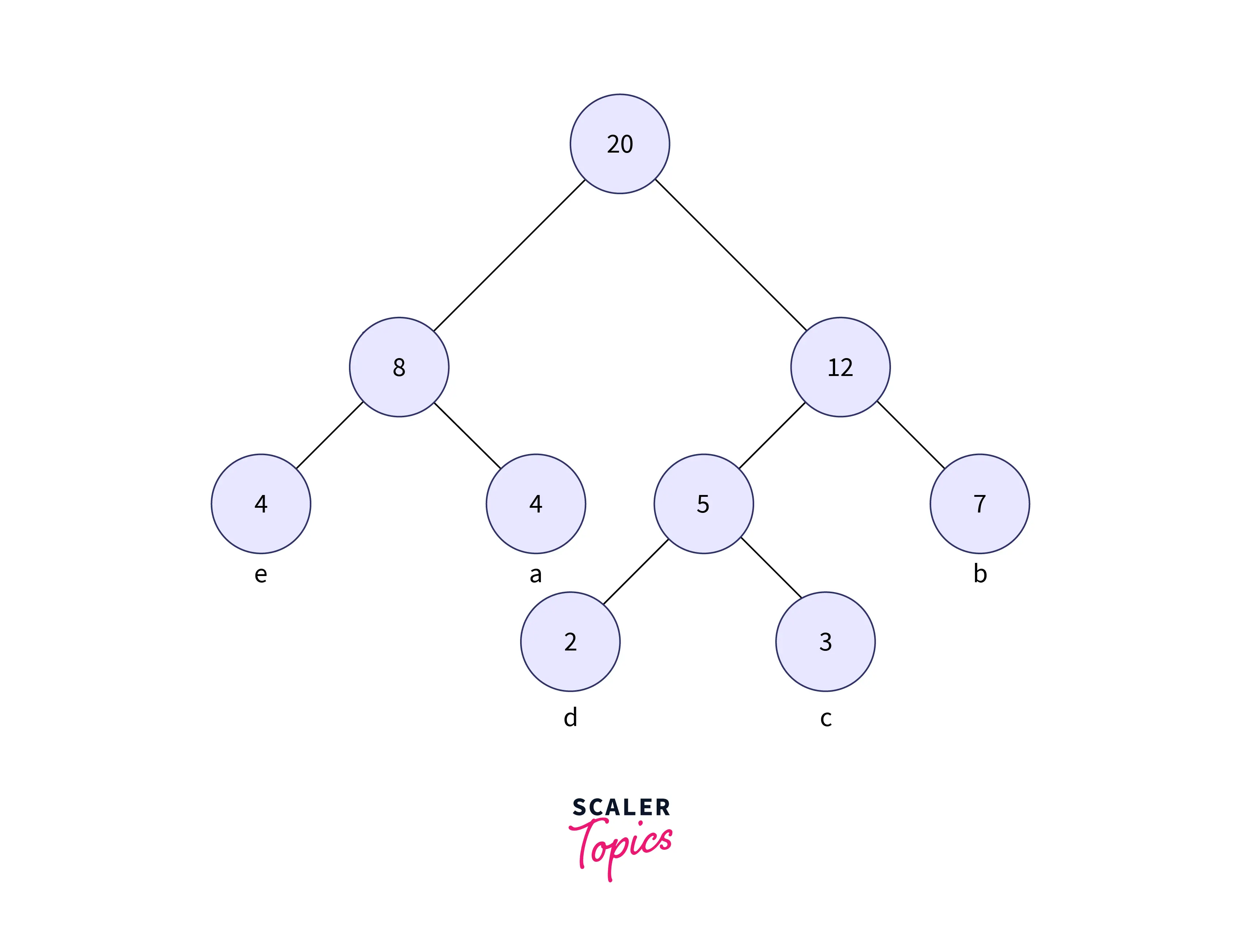
Repeat the procedure till all the unique characters are inserted into the tree. The above image is the Huffman tree formed for the given set of characters.
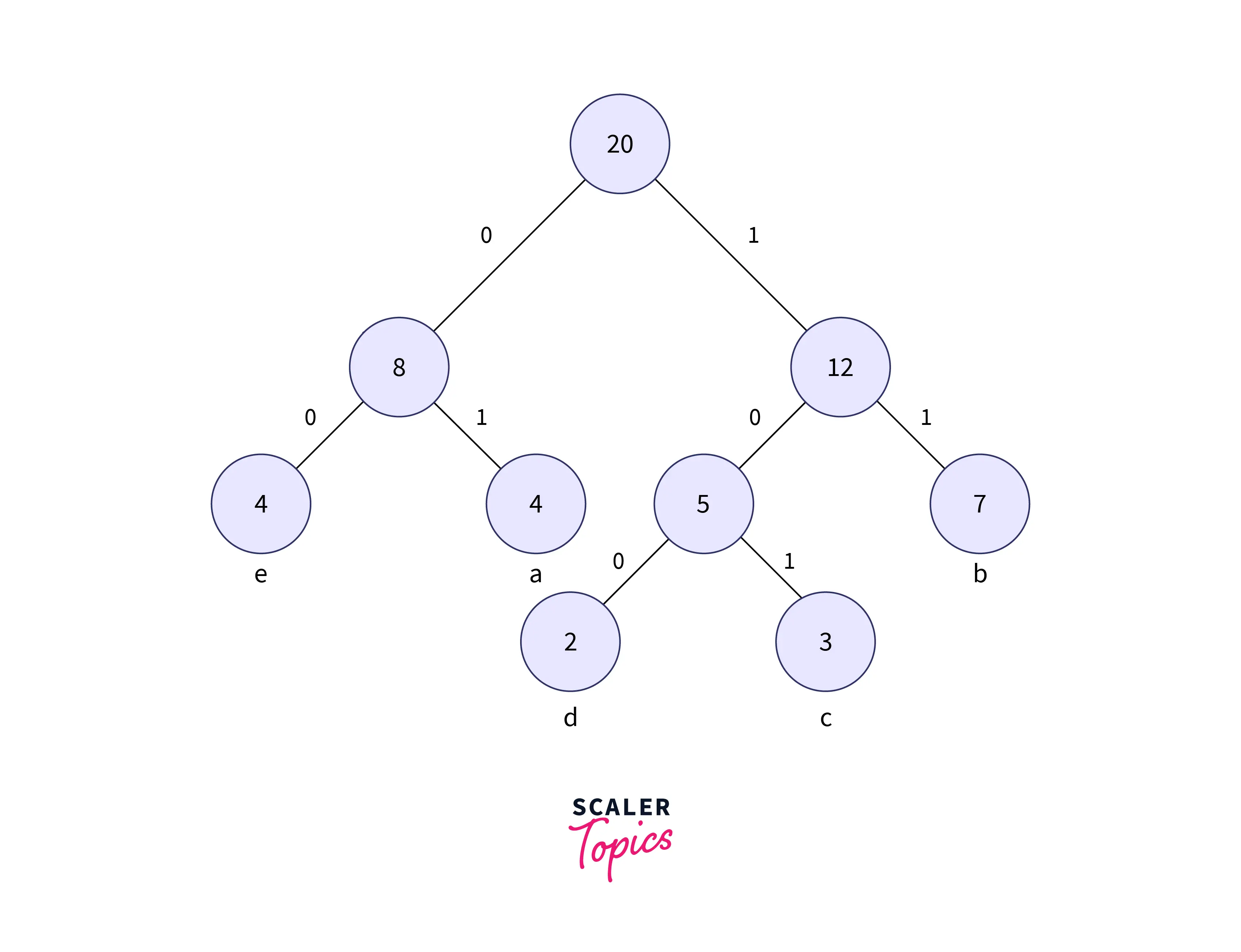
Now to form the code for each character, for each non-leaf node, assign 0 to the left edge and 1 to the right edge.
Rules to be followed while assigning weights for edges:
- If you assign weight 0 to the left edges, then we should assign weight 1 to the right edges.
- If you assign weight 1 to the left edges, then we need to assign weight 0 to the right edges.
- Any of the above two conventions can be followed.
- But use the same convention during decoding the tree as well.
The modified tree after assigning the weights is shown below:
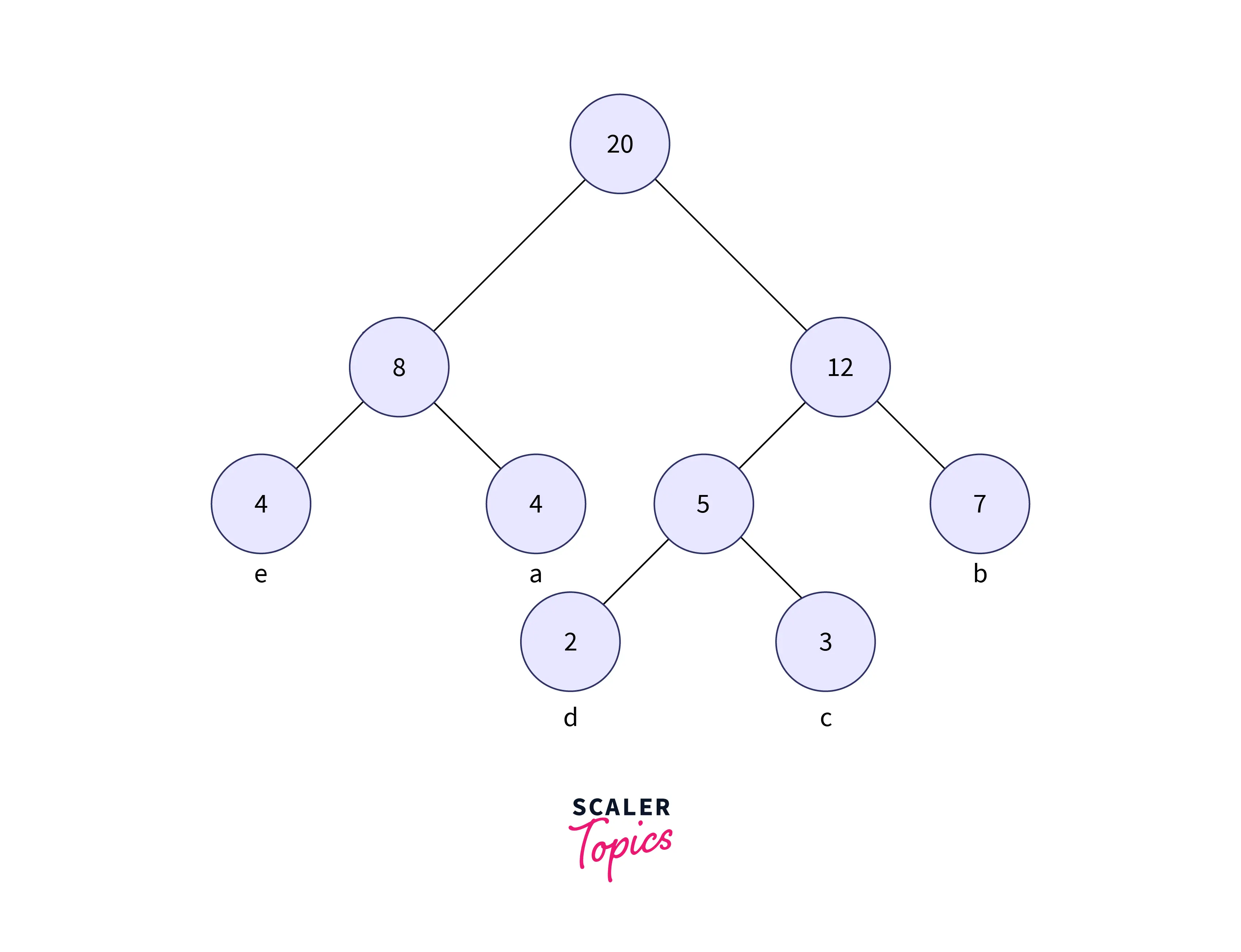
Decoding the Code
- For decoding the Huffman code for each character from the Huffman tree formed, we need to traverse through the Huffman tree until we reach the leaf node, where the element is present.
- While traversing, the weights across the nodes need to be stored and assigned to the elements present at the particular leaf node.
- This can be better explained using the example below:

- In the above image to get the code for each character, we need to traverse the full tree (until all leaf nodes are covered).
- Therefore the codes for every node are decoded with the help of the tree formed. The Code obtained for each character is shown below:
| Character | Frequency/count | Code |
|---|---|---|
| a | 4 | 01 |
| b | 7 | 11 |
| c | 3 | 101 |
| d | 2 | 100 |
| e | 4 | 00 |
Algorithm:
- Firstly create a priority queue Q1 consisting of each unique character from the given stream of data.
- Then sort them in the ascending order of their frequencies(this is can be done using a map/comparator).
- For all the unique characters present do the following:
- Create a newNode
- We need to draw the minimum value from the priority Queue and assign it to the left child of newNode which is formed.
- We need to draw the minimum value from priority Q and assign it to the right child of newNode which is formed.
- We need to calculate the sum of the two minimum values and assign it to the value of the newNode in the min-heap.
- Insert this newNode into the tree.
- Finally we need to return the root of the Huffman Tree formed.
Implementation of the above approach:
Python implementation of Huffman Coding:
# Huffman Coding implementation in python
class Node:
def __init__(self, freq, char, left=None, right=None):
# frequency of each character/symbol
self.freq = freq
# name of the character
self.char = char
# left node of current node
self.left = left
# right node of current node
self.right = right
# weightage of node (0/1)
self.huffman = ''
# utility function to print huffman
# codes for all symbols in the newly
# created Huffman tree
def printNodes(node, val=''):
# huffman code for the current node
newVal = val + str(node.huffman)
# if the node is not an edge node
# then do a traversal to the tree to get the values
if(node.left):
printNodes(node.left, newVal)
if(node.right):
printNodes(node.right, newVal)
# if the node is an edge node then
# display its huffman code
if(not node.left and not node.right):
print(f"{node.char} | {newVal}")
# unique characters from the given stream of data
chars = "abbcdbccdaabbeeebeab"
# frequency of each character
# calculated using the dictonary
dict_frequency={}
for i in chars:
if i in dict_frequency:
dict_frequency[i]+=1
else:
dict_frequency[i]=1
#inserting all the frequencies into the frequency array
freq=[]
for i in dict_frequency:
freq.append(dict_frequency[i])
# list of unused nodes
nodes = []
for x in range(len(freq)):
# appending the characters and frequency of
# each character into the huffman tree as a leaf node
nodes.append(Node(freq[x], chars[x]))
while len(nodes) > 1:
# sort all the nodes in an
# ascending order with respect to frequency using lambda function
nodes = sorted(nodes, key=lambda x: x.freq)
# extract the smallest two nodes
# and assign the values to the left and right child of the huffman tree
left = nodes[0]
right = nodes[1]
# assign weightage to these nodes
# assign the left node to 0 and the right node to 1
left.huffman = 0
right.huffman = 1
# combining these two smallest nodes to make the
# new node and this new node will be the parent node to them.
newNode = Node(left.freq+right.freq, left.char+right.char, left, right)
# now remove these two nodes and add their parent
nodes.remove(left)
nodes.remove(right)
nodes.append(newNode)
# repeat this process until all the characters are inserted in the tree
# Printing the Huffman Tree which if formed
print("Char| Huffman Code")
print("------------------")
printNodes(nodes[0])
Output:
Char| Huffman Code
------------------
a | 00
e | 01
d | 100
c | 101
b | 11
Java implementation of Huffman Coding:
//importing all the classes from different packages which have min-heap and comparator
import java.util.PriorityQueue;
import java.util.Scanner;
import java.util.Comparator;
// node class is the basic structure
// of each node present in the Huffman - tree.
class Huffman_Node{
// frequency of each character/symbol
int val;
//name of the character
char c;
//left node of the current node
Huffman_Node left;
// right node of the current node
Huffman_Node right;
}
// comparator class helps to compare the node
// this helps in extracting the minimum freq every time
class MyComparator implements Comparator<Huffman_Node>{
public int compare(Huffman_Node x, Huffman_Node y){
return x.val - y.val;
}
}
public class Huffman{
// recursive function to print the
// huffman-code through the tree traversal.
// Here s is the huffman - code generated.
public static void printCode(Huffman_Node root, String string1){
// if the left and right are null
// that means its a leaf node and we print
// the code s generated.
if (root.left == null && root.right == null && Character.isLetter(root.c)){
System.out.println( root.c + " | " + string1);
return;
}
// assign weight to nodes: if left add 0 to code
// if right adds 1 to the code.
// recursive calls for left and
// right sub-tree of the generated tree.
printCode(root.left, string1 + "0");
printCode(root.right, string1 + "1");
}
// main function
public static void main(String[] args){
// number of unique characters in the given string.
int n = 5;
//given string of frequency specified
char[] arr = { 'a', 'b', 'c', 'd' , 'e' };
//frequency of each character
int[] freq = { 4, 7, 3, 2, 4 };
// Huffman tree is created
// makes a min-priority queue(min-heap).
PriorityQueue<Huffman_Node> Qu
= new PriorityQueue<Huffman_Node>(n, new MyComparator());
//traverse the loop until all characters are inserted in the tree
for (int i = 0; i < n; i++){
// creating the leaf node for all unique characters
Huffman_Node Hf_Node = new Huffman_Node();
Hf_Node.c = arr[i];
Hf_Node.val = freq[i];
Hf_Node.left = null;
Hf_Node.right = null;
// add functions add
// the huffman node to the queue.
Qu.add(Hf_Node);
}
// create a root node
Huffman_Node root = null;
// repeat this process until all the characters are inserted in the tree
while (Qu.size() > 1){
// first min extract.
Huffman_Node node1 = Qu.peek();
Qu.poll();
// second min extract.
Huffman_Node node2 = Qu.peek();
Qu.poll();
// new node f which is equal to the sum of both these extracted nodes
Huffman_Node f1 = new Huffman_Node();
// to the sum of the frequency of the two nodes
f1.val = node1.val + node2.val;
f1.c = '-';
// extract the smallest two nodes
// and assign the values to the left and right child of the huffman tree
f1.left = node1;
f1.right = node2;
// combining these two smallest nodes to make the
// new node and this new node will be the parent node to them.
root = f1;
// add this node to the priority queue.
// repeat this process until all the characters are inserted in the tree
Qu.add(f1);
}
// Printing the Huffman Tree which if formed
System.out.println("Char | Huffman code ");
System.out.println("--------------------");
printCode( root, "");
}
}
}
Output:
Char| Huffman Code
------------------
a | 00
e | 01
d | 100
c | 101
b | 11
C++ implementation of Huffman Coding:
#include <bits/stdc++.h>
using namespace std;
// A Huffman tree node
struct Huffman_Node{
// Taking one of the input characters
char data;
// Frequency of each character
unsigned freq;
// Left and right child of the tree
Huffman_Node *left, *right;
Huffman_Node(char data, unsigned freq){
left = right = NULL;
this->data = data;
this->freq = freq;
}
};
// compare helps to compare the node
// this helps in extracting the minimum freq every time
struct Compare {
bool operator()(Huffman_Node* l, Huffman_Node* r){
return (l->freq > r->freq);
}
};
// Prints huffman codes from the formed tree
void print_Tree(struct Huffman_Node* root, string str){
if (!root)
return;
// it means it reached the leaf node and print the code
if (root->data != '#')
cout << root->data << " | " << str << "\n";
// assign weight to nodes: if left add 0 to code
// if right adds 1 to the code.
// recursive calls for left and
// right sub-tree of the generated tree.
print_Tree(root->left, str + "0");
print_Tree(root->right, str + "1");
}
// The main function that builds a Huffman Tree and
// print codes of each character by traversing the built Huffman Tree
void HuffCodes(char data[], int freq[], int size){
struct Huffman_Node *left, *right, *top;
// Create a min heap & inserts all characters of data[]
priority_queue<Huffman_Node*, vector<Huffman_Node*>, Compare> Min_Heap;
for (int i = 0; i < size; ++i)
Min_Heap.push(new Huffman_Node(data[i], freq[i]));
// Iterate while the size of the heap doesn't become 1
while (Min_Heap.size()!=1){
// Extract the two minimum
// freq items from min heap
left = Min_Heap.top();
Min_Heap.pop();
right = Min_Heap.top();
Min_Heap.pop();
// Create a new internal node with
// frequency equal to the sum of the left and right node
// Add this node to the min heap '#' is a special value
// for internal nodes, not used
top = new Huffman_Node('#', left->freq + right->freq);
top->left = left;
top->right = right;
Min_Heap.push(top);
}
// Print Huffman codes using the Huffman tree built above
cout << "Char | Huffman code ";
cout << "\n----------------------\n";
print_Tree(Min_Heap.top(), "");
}
// Driver Code
int main(){
//given a char array consisting of unique characters
char arr[] = { 'a', 'b', 'c', 'd' , 'e' };
//an int array which tells the frequency of each character
int freq[] = { 4, 7, 3, 2, 4 };
//To find the size
int S = sizeof(arr) / sizeof(arr[0]);
//For finding Huffman code for each character
HuffCodes(arr, freq, S);
return 0;
}
Output:
Char| Huffman Code
------------------
a | 00
e | 01
d | 100
c | 101
b | 11
Javascript implementation of Huffman Coding
<script>
// node class is the basic structure of each node in the Huffman tree.
class HuffmanNode {
// constructor for the HuffmanNode
constructor() {
this.data = 0;
this.c = '';
this.left = this.right = null;
}
}
// recursive function to print the huffmancode of each character through the tree traversal.
// Here is the huffman code generated for a character.
function printHuffmanCode(root,a) {
// base case; if the left and right are null then its a leaf node and we print
// the code a which is generated by traversing the huffman tree.
if (root.left == null && root.right == null && (root.c).toLowerCase() != (root.c).toUpperCase()) {
// c is the character in the node
document.write(root.c + " -> " + a+ "<br>");
return;
}
// if we go to the left then add "0" to the code according to the rule followed
// if we go to the right add"1" to the code.
// recursive calls for left and
// right sub-tree of the generated tree.
printCode(root.left, a + "0");
printCode(root.right, a + "1");
}
// main function (driver code)
// number of characters in the given string.
let n = 6;
let char_array = [ 'a', 'b', 'c', 'd', 'e'];
let char_freq = [ 4, 7, 3, 2, 4 ];
// creating a priority queue q.
let que = [];
for (let i = 0; i < n; i++) {
// creating a Huffman node object
// and add it to the priority queue.
let hn = new HuffmanNode();
hn.c = char_array[i];
hn.data = char_freq[i];
hn.left = null;
hn.right = null;
// add functions add
// the huffman node to the queue.
que.push(hn);
}
// create a root node
let root = null;
que.sort(function(a,b){return a.data-b.data;});
// Here we will extract the two minimum values from the heap each time until
// its size reduces to 1, extract until all the nodes are extracted
while (que.length > 1) {
// first extract the min from the min heap
let x = q[0];
que.shift();
// extract the second min from the min heap
let y = q[0];
que.shift();
// new node f which is equal
let f = new HuffmanNode();
// to the sum of the frequency of the two nodes assigning values to the f node.
f.data = x.data + y.data;
f.c = '-';
// first extracted node as a left child.
f.left = x;
// second extracted node as the right child.
f.right = y;
// marking the f node as the root node.
root = f;
// add this node to the min heap.
que.push(f);
que.sort(function(a,b){return a.data-b.data;});
}
// print the codes by traversing the tree
printHuffmanCode(root, "");
</script>
Output:
a -> 00
e -> 01
d -> 100
c -> 101
b -> 11
Explanation:
The Huffman Tree is formed and decoded by traversing. When it reaches the leaf node, then the values obtained by traversing are to be assigned to the character present at the leaf node. This way Huffman Code is obtained for each unique character present in the given stream of data.
Huffman Coding Complexity
- Time complexity: O(N logN)
- The time taken for encoding each given unique character depending on its frequency is O(N logN) where N is the number of unique given characters.
- Getting minimum from the priority queue(min-heap): time complexity is O(log N) since it calls minHeapify method.
- And extractmin() is called for 2*(N-1) times.
- Therefore the overall complexity of Huffman Coding is considered to be O(N logN).
- Space Complexity: O(N)
- The space complexity is O(N) because there are N characters used for storing them in a map/array while calculating their frequency.
Disadvantages of Huffman Coding
In this section let’s discuss the disadvantages of Huffman Coding and why it is said to be not optimal always:
- It is not considered to be optimal unless all probabilities/frequencies of the characters are the negative powers of 2.
- Although by grouping symbols and extending the alphabet, one may come closer to the optimal, the blocking method requires a larger alphabet to be handled. So, sometimes Huffman coding is not that effective at all.
- Counting the frequency of each symbol/character has many efficient methods in spite of that, it can be very slow when rebuilding the entire tree for each symbol/character. This is usually the case when the alphabet is big and the probability distributions change rapidly with each symbol.
Greedy Algorithm for Constructing a Huffman Code
- Huffman invented a greedy algorithm that creates an optimal prefix code called a Huffman Code for every unique character from the given stream of data.
- The algorithm builds the Huffman tree in a bottom-up manner using the minimum nodes every time.
- This is called a greedy approach because each character gets its length of code depending on its frequency in the given stream of data. If the size of the code obtained is smaller, then it means it is a frequently occurring element in the data.
Important Formulas
In this section, we discuss the few important formulas required to estimate the size of the given data stream after compilation i.e(after forming the Huffman Tree and assigning codes for each unique character).
The total size which is required now:
- Average code length:=

= { (4 x 2) + (4 x 2) + (2 x 3) + (3 x 3) + (7 x 2)} / (4 + 4 + 2 + 3 + 7)
= 2.25
- Length of Huffman Encoded Message: Total number of bits in Huffman encoded message = Total number of characters in the message x Average code length per character(obtained from the above formula)
= 20 * 2.25
= 45 bits
Applications of Huffman Coding
Here we will be discussing the real-life applications of Huffman Coding:
- Huffman Coding is frequently used by conventional compression formats like PKZIP, GZIP, etc.
- For data transmission using fax and text, Huffman Coding is used because it reduces the size and improves the speed of transmission.
- Many multimedia storage like JPEG, PNG, and MP3 use Huffman encoding(especially the prefix codes) for compressing the files.
- Image compression is mostly done using Huffman Coding.
- It is more useful in some cases where there is a series of frequently occurring characters to be transmitted.
Conclusion
- Huffman Coding is generally useful to compress the data in which there are frequently occurring characters.
- We can observe that the most frequent character gets the smallest code and the least frequent character gets the largest code.
- The variable-length code i.e, a different number of bits for each character/symbol is obtained by using the Huffman Code compression technique which is more advantageous than fixed-length coding because it reduces the memory space and decreases the time required for transmitting the data
- To gain a better understanding of Greedy Algorithm, go through this article.