How to Reverse a Stack Using Recursion?

Given a stack, write a program to reverse the order of the elements inside the stack using recursion. The element at the top should be moved to the bottom and so on. This program must use only standard stack operations – push(item), pop(), top(), size(), and isEmpty().

Example:

Input: $23, 56, 82, 90$

Output: $90, 82, 56, 23$

Here, $23$ is at the top in the input whereas, $90$ is at the top of the stack in the output.

Input: $8$

Output: $8$

Reverse a Stack Using Recursion

To reverse a stack using recursion the idea is very simple, we will pop the elements of the stack one by one and hold them in the Function Call Stack until the stack is empty. The function call stack is a dynamic data structure that stores all the active function calls in a stack. When the stack is empty we start inserting all the elements back into the stack one by one at the bottom of the stack reserving the position of the rest of the elements.

Illustration

Step 1:

Let us dry-run the above on the example method to reverse a stack using recursion to get the output. First of all, we are supposed to store all the elements of the stack in the auxiliary stack i.e. Function Call Stack until the given stack is not empty.

As only the top is available in the stack the order of the elements is already reversed when added to the auxiliary stack. This is done until the stack is not empty.

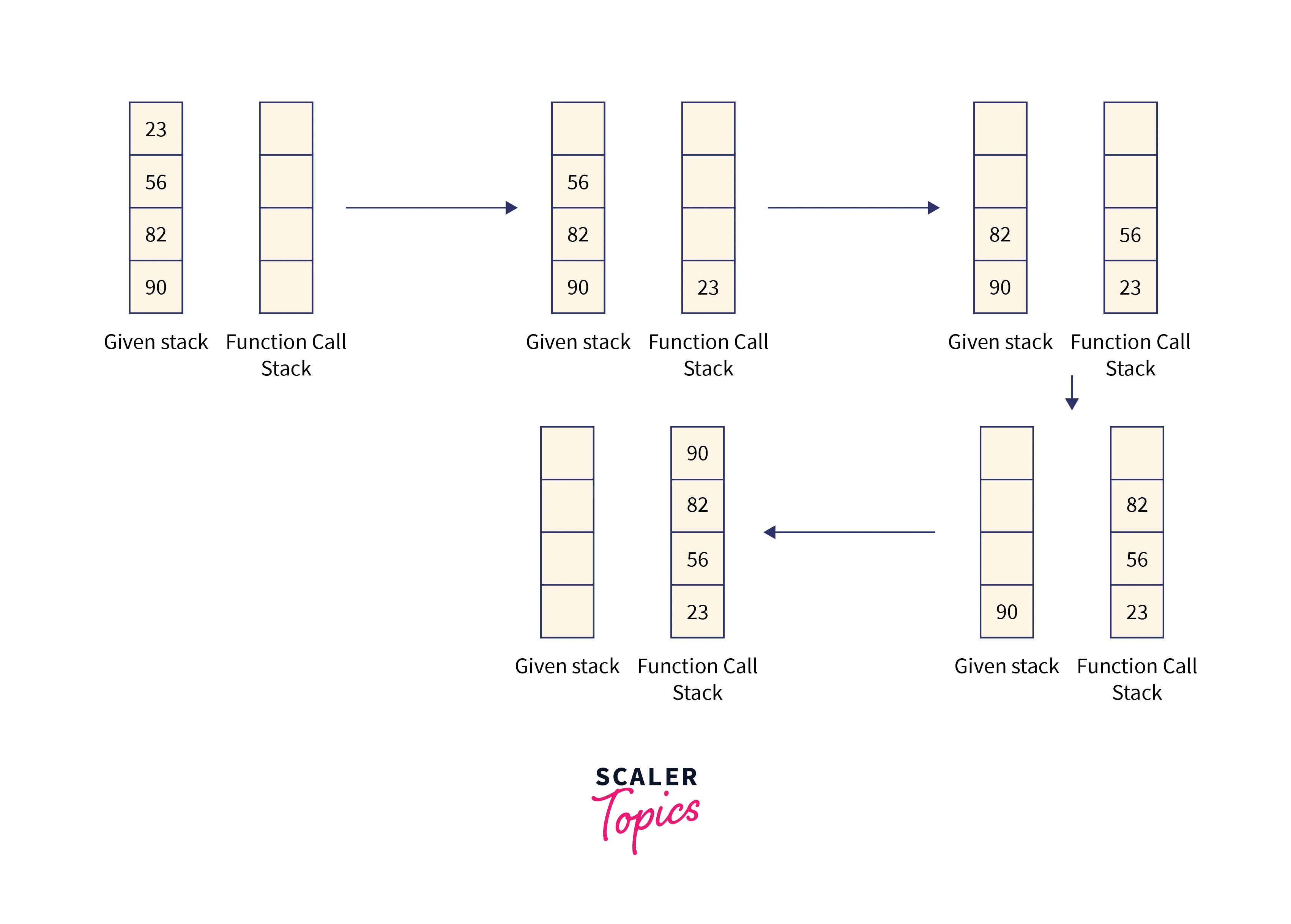
First of all, we recursively called a function that pops the top element of the stack and calls the same function on the remaining elements of the stack. If the stack is empty, we no longer make recursive calls.

Step 2:

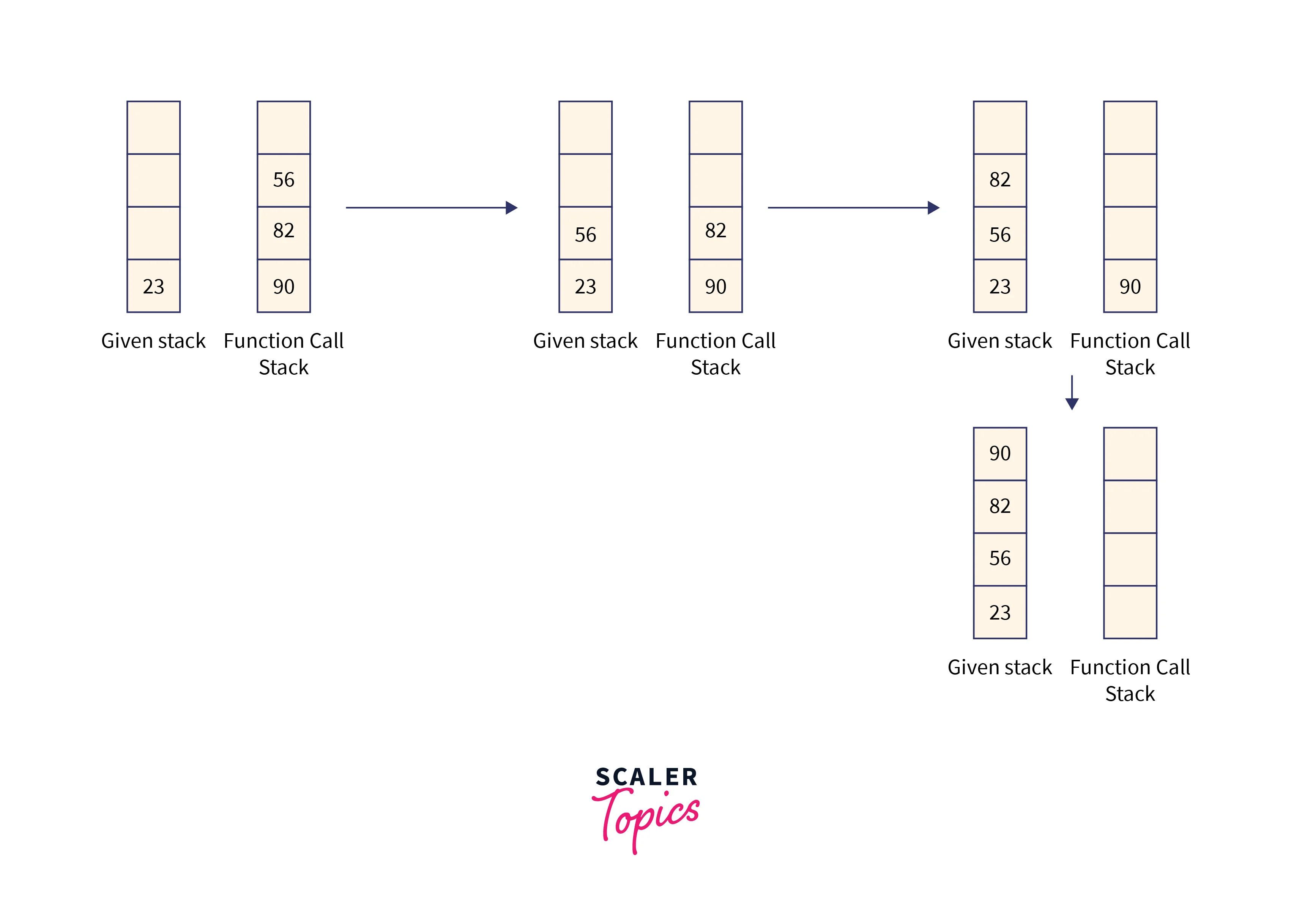
Once the stack is empty and we return we add the elements back to the stack one by one but at the bottom of the stack.

In recursion, once the base condition is reached we start returning to the parent function calls. So once our stack is empty, we will return to the previous or parent function. This parent will add the element stored at the top of the function call stack to the bottom of the stack and return to its parent function call.

As function call also uses the stack data structure the order of execution will be First in Last out. This implies that the recent function will be called first and the very first function call will be addressed at the end.

Step 3:

We are supposed to add the current element at the bottom. To facilitate this we will create a separate function that will empty the stack first, push the current element, and then again push back all the elements in the same order as they were.

Again this functionality can be achieved using recursion. We can recursively call this new function until the stack is not empty. As soon as the stack is empty we push the current element and then push the rest of the elements.

The order of the elements will be reserved as we are using recursion i.e. stack itself.

Let us dry-run this as well for the last element.

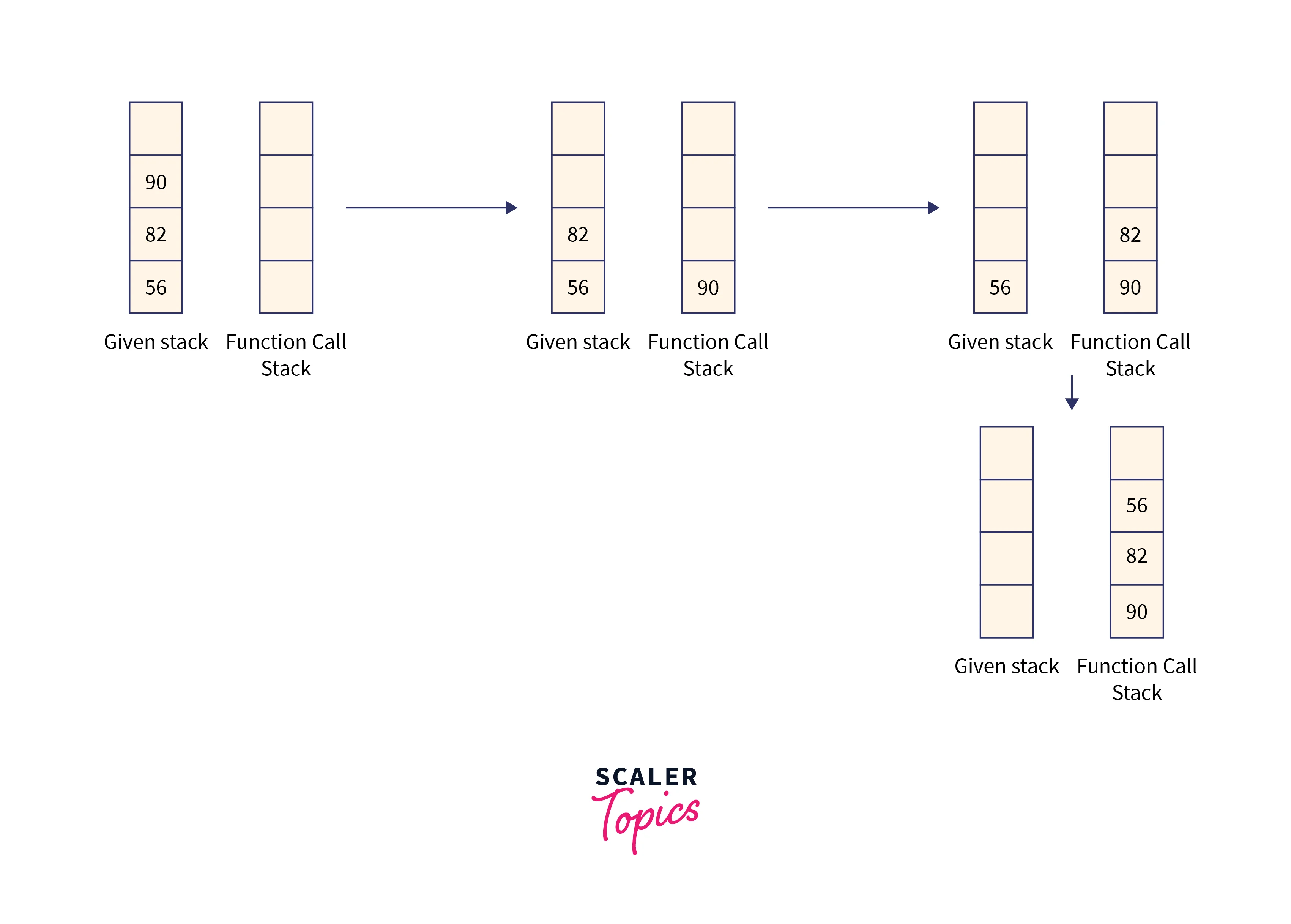
Now, we will add 23 to the bottom pop each element from the auxiliary stack, and push it back to the original array.

Note: The auxiliary spaces used here and in the previous section are different.

Steps to Implement

• Create a stack and push the elements inside it.
• Create a reverse() function which can be called from the main function.
• This reverse() function will recursively store the current element and call the reverse function for the rest of the elements until the stack is empty.
• At the end of the reverse() function we will call insertAtBottom() function.
• Create insertAtBottom() function which will again pop all the elements of the stack recursively and insert the current element at the bottom.
• Print the stack. The task, reverse a stack using recursion is completed.

Code Implementation

#include <bits/stdc++.h>
using namespace std;

// Recursive function to insert an element at the bottom of a stack.
void insert_at_bottom(stack<int>& st, int x)
{
    if (st.size() == 0) {
        st.push(x);
    }
    else {
        // Hold the top item and recurse to insert the new element at the bottom.
        int top_item = st.top();
        st.pop();
        insert_at_bottom(st, x);

        // Push back the held item to maintain the original order above the new element.
        st.push(top_item);
    }
}

// Function to reverse the given stack using insert_at_bottom().
void reverse(stack<int>& resultant_stack)
{
    if (resultant_stack.size() > 0) {
        // Hold the top item and recurse to reverse the remaining stack.
        int top_item = resultant_stack.top();
        resultant_stack.pop();
        reverse(resultant_stack);

        // Insert the held item at the bottom, effectively reversing the stack.
        insert_at_bottom(resultant_stack, top_item);
    }
    return;
}

int main()
{
    stack<int> initial_stack, resultant_stack;
    initial_stack.push(23);
    initial_stack.push(56);
    initial_stack.push(82);
    initial_stack.push(90);

    resultant_stack = initial_stack;

    cout << "Original Stack" << endl;
    while (!initial_stack.empty()) {
        cout << initial_stack.top() << " ";
        initial_stack.pop();
    }
    cout << endl;

    reverse(resultant_stack);
    cout << "Reversed Stack" << endl;
    while (!resultant_stack.empty()) {
        cout << resultant_stack.top() << " ";
        resultant_stack.pop();
    }
    return 0;
}

Output

Original Stack
90 82 56 23 
Reversed Stack
23 56 82 90 

The output prints the original stack and the modified reverse stack. We start printing from the top and go to the bottom.

Complexity Analysis

Time Complexity: $O(N^2)$

The time complexity can be derived as follows:

$T(n) = T(n-1) + n$ // after popping one item

$= T(n-2) + (n-1) + n$ // after popping two items

$= T(n-3) + (n-2) + (n-1) + n$ // after popping three items

The final relationship is represented by:

$T(n) = T(n-(n-1)) + T(n-(n-2)) + … + (n-2) + (n-1) + n$

$= T(1) + T(2) + … + (n-2) + (n-1) + n$

$= 1 + 2 + … + (n-2) + (n-1) + n$

$= n * (n+1)/2$

On simplifying we get the time complexity as $O(N^2)$.

We are using two functions reverse() and insertAtBottom(). The time complexity can be explained as follows:

• The inserAtBottom function removes all the elements from the stack one by one using recursion and then adds the element at the bottom and then adds all the elements back to the stack. This takes $O(N)$ time to take the worst case where several elements in the stack are N.
• The reverse() function is run N times and each time it calls insertAtBottom() the overall time complexity becomes $O(N^2)$.

Space Complexity: $O(N)$

The space complexity for the call stack during recursion is $O(N)$, as each recursive call adds a new element to the frame of the call stack. Here, N is the number of elements.

Additionally, we are using a constant amount of space.

FAQs

Q. How does recursion help in reversing the stack?

A. Recursion utilizes the call stack to store the elements of the stack in reverse order and these are then inserted at the bottom of the original stack one by one.

Q. Is there any alternative approach with better time complexity?

A. Yes of course. We can use another data structure like array, stack, or queue to reverse the original stack.

Q. What is the practical application of reversing the stack?

A. Reversing a stack can be part of algorithms involving backtracking, parsing, and certain data structure transformations.

Q. What are the limitations of this approach?

Ans. As we are using a recursive approach it won’t be efficient for the larger stack. The time complexity is $O(N^2)$ and for space, it uses a call stack making it less memory-efficient.

Conclusion

• Recursion is a very powerful technique and it can be useful in many problem-solving applications.
• In this approach to reverse a stack using recursion, we are using two recursive functions reverse() and insertAtBottom().
• The reverse() function recursively stores the element in the call stack and calls the insertAtBottom() method.
• The insertAtBottom() method recursively pops the element until the stack is not empty, adds the current element, and then adds all the elements back to the stack in the same order.
• The time complexity is $O(N^2)$ and space complexity is $O(N)$ to reverse a stack using recursion. This method is not very efficient when the stack size is large.