The Greedy algorithm solves optimization problems by making locally optimal choices, potentially leading to a globally optimal solution. This article covers the approach, related terms, and discusses its applications, including finding optimal solutions and approximating solutions for NP-Hard problems like the Traveling Salesman Problem.
Takeaways
Applications of Greedy Algorithm
- Finding an optimal solution (Activity selection, Fractional Knapsack, Job Sequencing, Huffman Coding).
- Finding close to the optimal solution for NP-Hard problems like TSP.
What is Greedy Algorithm?
To maximize the amount you take, you’ll obviously start with the $20 pile. If you’re able to finish that pile in under one minute, then you’ll move to the $10 pile (and not the $5 pile). If you’re extremely fast here too, then finally you’ll go for the $5 pile.
This is an example of the greedy approach. To maximize the amount of money you take, you start with the most desirable solution at that point of time. You don’t worry about whether this choice will hurt your profit in the coming future.
A greedy algorithm refers to any algorithm employed to solve an optimization problem where the algorithm proceeds by making a locally optimal choice (that is a greedy choice) in the hope that it will result in a globally optimal solution.
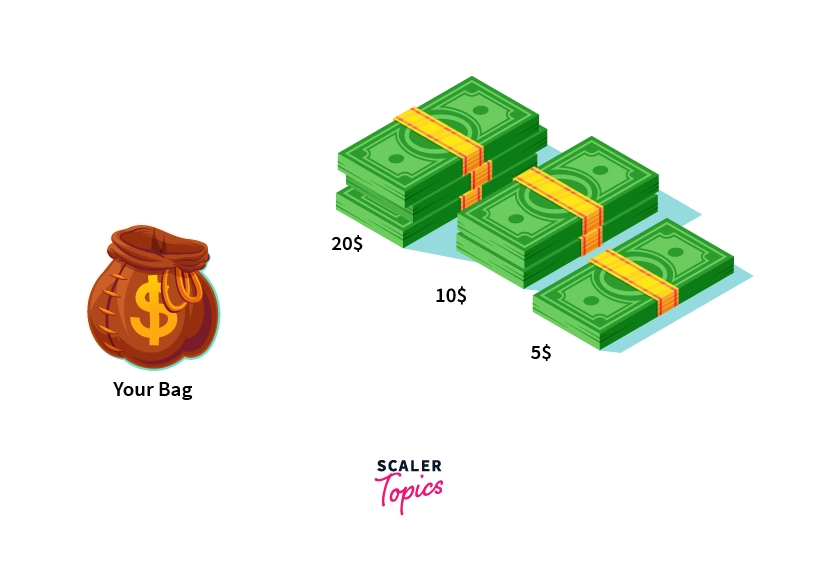
In the above example, our greedy choice was taking the currency notes with the highest denomination.
Characteristics of Greedy Algorithm
- Greedy algorithms make the best choice at each step without reconsideration.
- Decisions made are final and cannot be changed.
- They may not always find the best solution and can sometimes yield suboptimal results.
- Despite this, they are fast compared to other methods like dynamic programming.
- Greedy algorithms are intuitive but challenging to prove their correctness mathematically.
- In some cases, they can provide near-optimal solutions when an exact solution is impractical.
Why To Use Greedy Algorithm?
- In many cases
greedy algorithmis the most intuitive approach to solve a given optimization problem, that is, it is often the first-guessed solution and is easy to formulate. - Correct greedy algorithms are often more powerful and fast as compared to other approaches such as dynamic programming. This is because the greedy approach has to consider only one locally optimal choice while moving ahead with the solution, while dynamic programming must check all possible cases.
Greedy algorithmswork for a wide range of problems, many of which have real-life applications in fields such as designing networking protocols and scheduling multiple events.
Architecture Of Greedy Algorithm
The basic architecture of the implementation of any greedy algorithm is as follows:
Input to Algorithm:
Function = F, Set of Inputs = C
Output:
Solution Set Which Maximizes or Minimizes Function
Steps:
1. Start with an empty solution set, S.
2. While there are still choices in the candidate set (C):
- Choose an item from C.
- If the chosen item is feasible:
- Add it to the solution set S.
- Remove the chosen item from C.
3. Return the solution set S. Here:
Select()function makes a greedy choice from the input setCisFeasable()function checks whether the choice made bySelect()function leads to an optimal value ofF
Properties of Greedy Algorithm
There is no defined mathematical way to check the correctness of a given greedy algorithm. But it has been observed that many optimization problems that can be solved using some greedy algorithm satisfy 2 properties as given below:
- Greedy choice property
- Optimal substructure property
To understand these 2 properties in a better way, we will make use of an example problem.
The Indian Coin Change Problem
If we want to make a change for $X$ rupees, and we have an infinite supply of each of the denominations in Indian currency, that is, ${1, 2, 5, 10, 20, 50, 100, 500, 1000}$ valued coins, what is the minimum number of coins needed to make the change?
Greedy Choice Property
- A problem is said to exhibit greedy choice property if the globally optimal solution can be reached by making locally optimal (greedy) choices. These choices are not dependent on our future choices, and can not be altered after they have been made.
- It is equivalent to showing that there is an optimal solution to the problem that is obtained by only greedy choices.
It can be seen using brute force solutions that the optimal solution for some $X$, say 76, is made up of greedy choices only as follows:
$\ce{76 ->[-50] 26->[-20] 6->[-5] 1->[-1]0}$
So the solution set comprising of the minimum number of coins required for exchange is ${1,5,20,50}$.
As we can see, it consists of all the greedy choices, that is, choosing the coin of the largest denomination that is equal to or less than the value of the amount left.
Optimal Substructure
A problem is said to exhibit optimal substructure property if the global optimal solution to the said problem can be constructed by combining the greedy choice made with optimal solutions to the subproblem of the original problem.
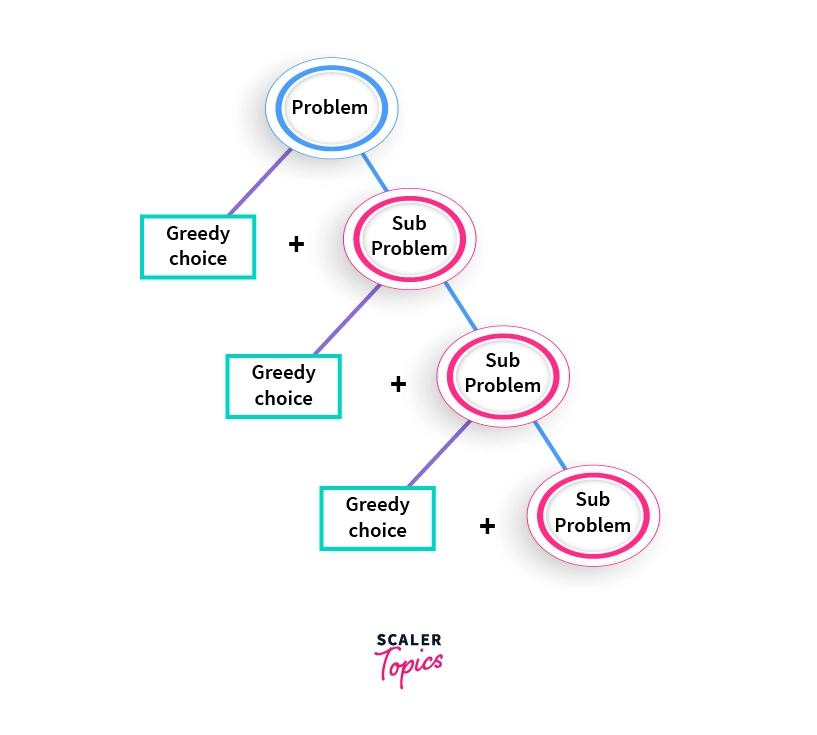
Schematic Diagram of Optimal Substructure
Let’s break the above problem (for $X = 76$) into 2 parts:
- The greedy choice: Choosing the largest possible coin denomination $\le$ 76, that is the coin with value 50.
- The Subproblem: Applying our greedy algorithm on $Y = X-50 = 26$. As was seen above, the solution set for the subproblem is ${20, 5, 1}$.
- Combining Solutions: Combining the greedy choice with the solution set of the subproblem, we get
${50}\cup{20, 5, 1} = {50, 20, 5, 1}$
Advantages Of Greedy Algorithm
- All
greedy algorithmsare very intuitive and can be guessed easily. Greedy algorithmsare generally easy to understand as well as implement.- If correct,
greedy algorithmsfind the optimal solution much faster as well more efficiently than its alternatives, such as dynamic programming.
Disadvantages Of Greedy Algorithm
- Though very intuitive, it is very hard to prove mathematically the correctness of a greedy algorithm to solve the given problem at hand.
- A
greedy approachto solve optimization problems may not always be correct, may even lead to the worst possible solution (as in the case of the Travelling Salesman Problem).
Ready to conquer complex algorithms? Our Dynamic Programming Course is your ticket to success. Enroll today and elevate your coding proficiency!
Conclusion
Greedy algorithmrefers to a class of algorithms that use a greedy approach to find the optimal solution to some optimization problem.- In any
greedy algorithm, the current choice is made such that it is the best choice at that moment, without worrying about the future consequences of the said choice. Once made, this choice is never altered. - Though intuitive, it is very hard to prove the correctness of the algorithm.
Greedy algorithmdoes not always lead to the global optimal solution.- A correct
greedy algorithmis very fast and efficient as compared to other algorithms, such as dynamic programming. - All problems which can be solved using a greedy approach exhibit greedy choice and optimal substructure properties.