Graph algorithms are vital for analyzing interconnected data structures, enabling tasks like pathfinding and connectivity analysis in social networks and GPS systems. From route optimization to recommendation engines, they drive insights and optimizations across various domains. Their applications extend to fields like bioinformatics and logistics, showcasing their broad relevance in modern computing and problem-solving.
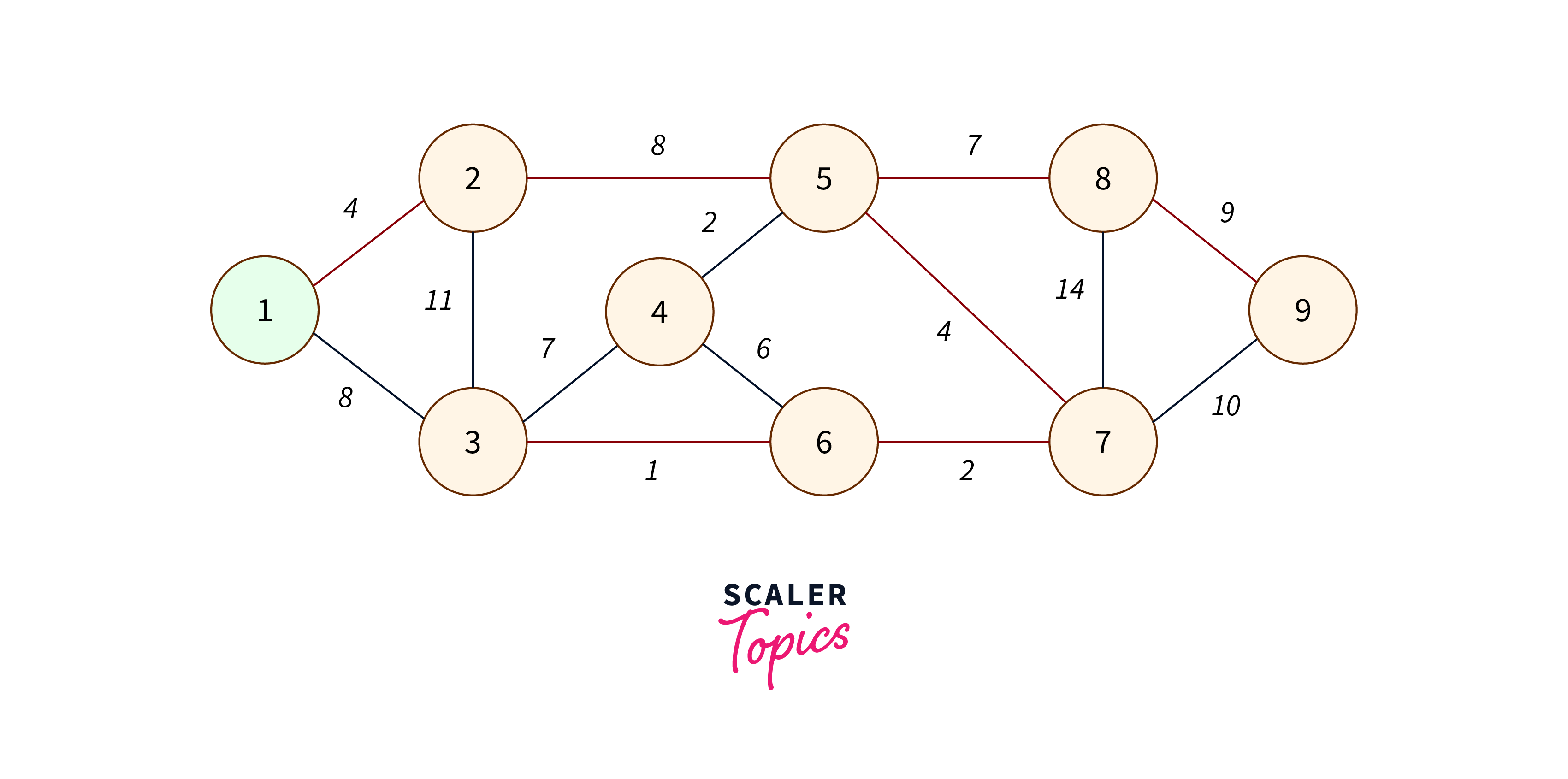
What is a Graph?
A graph comprises a finite collection of vertices or nodes and a series of edges linking these vertices. Vertices are considered adjacent if they share a connecting edge.
Below are some fundamental concepts related to graphs:
- Order: Denotes the total count of vertices within the graph.
- Size: Represents the total number of edges present in the graph.
- Vertex Degree: Indicates the number of edges incident to a particular vertex.
- Isolated Vertex: Refers to a vertex that lacks connections to any other vertices within the graph.
- Self-Loop: Occurs when an edge connects a vertex to itself.
- Directed Graph: A graph where edges possess directionality, indicating start and end vertices.
- Undirected Graph: Characterized by edges lacking directional attributes.
- Weighted Graph: Features edges with assigned weights.
- Unweighted Graph: Contains edges without associated weights.
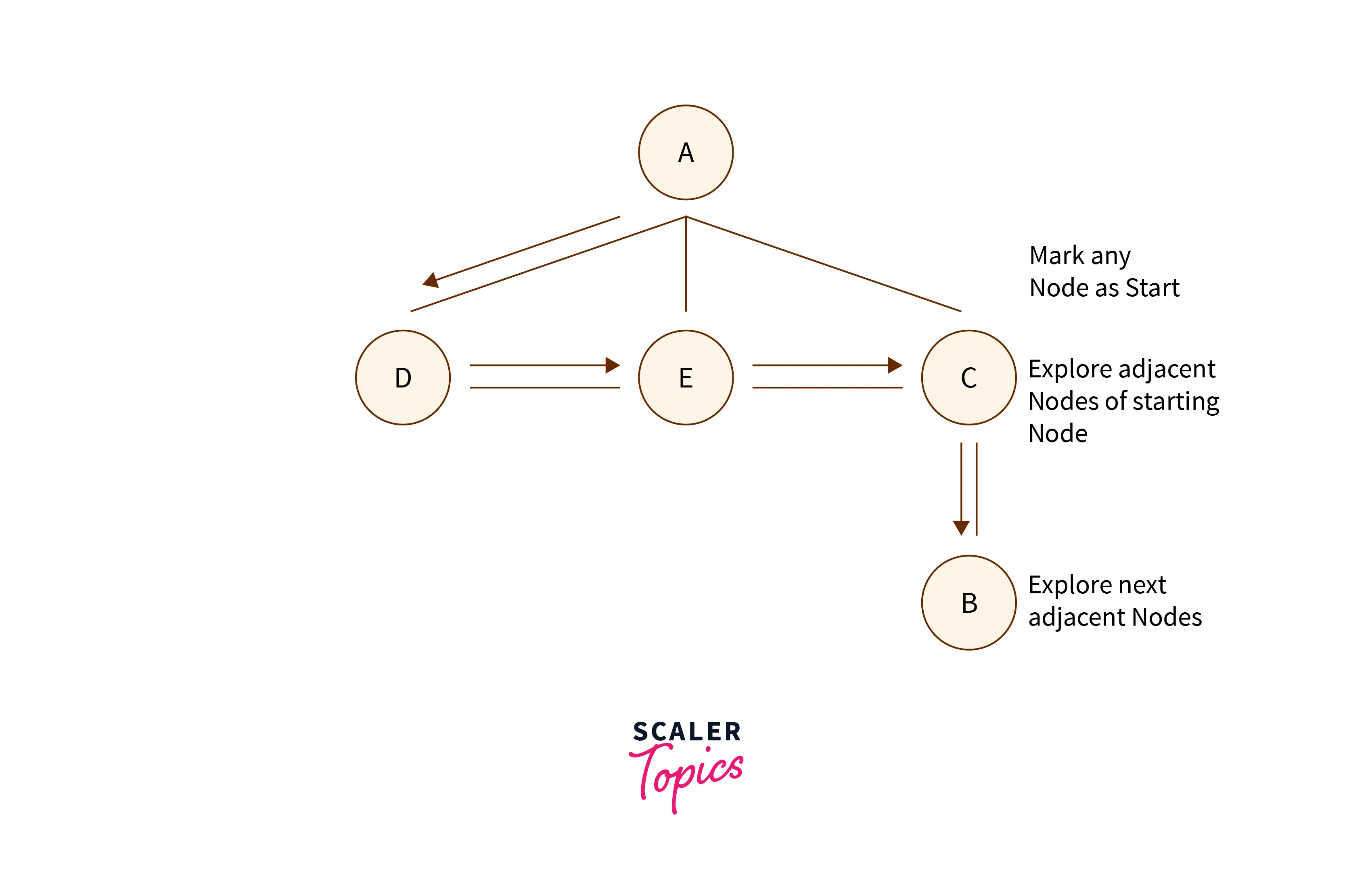
Breadth First Search (BFS)
Breadth-first search (BFS) is a fundamental graph traversal algorithm used to explore nodes in a graph. It systematically visits all nodes at a certain depth before moving on to the next level. By employing a queue data structure, BFS ensures that nodes are visited in a breadthward motion, making it particularly useful for finding the shortest path in unweighted graphs.
Algorithm of BFS
- Initiate the process by appending any vertex from the graph to the rear of the queue.
- Extract the front item from the queue and include it in the list of visited nodes.
- Generate nodes for the adjacent vertices of the current node and insert those that have not yet been visited.
- Repeat steps two and three until the queue becomes empty.
Pseudocode of Breadth First Search Algorithm
Create a Queue (say Q)
Mark the initial Vertex V => Visited.
Add V to the Queue-Q
WHILE Queue-Q is not empty:
Remove an element from the front of Queue-Q
Store that element in Vertex (say U)
Loop over all the Unvisited Neighbors of Vertex-U
Mark the neighbor as Visited
Add the Neighbor to the Q.
Complexity: 0(V+E) where V is vertices and E is edges.
Applications of BFS
- Shortest Path Finding: Breadth-First Search (BFS) in graph algorithms is utilized to find the shortest path between two vertices in an unweighted graph.
- Network Analysis: BFS aids in traversing and analyzing networks, such as social networks or the internet, to understand connectivity patterns.
- Minimum Spanning Tree (MST): BFS is utilized to construct a Minimum Spanning Tree, ensuring the most cost-effective connection of all vertices in a graph, commonly applied in network design and optimization.
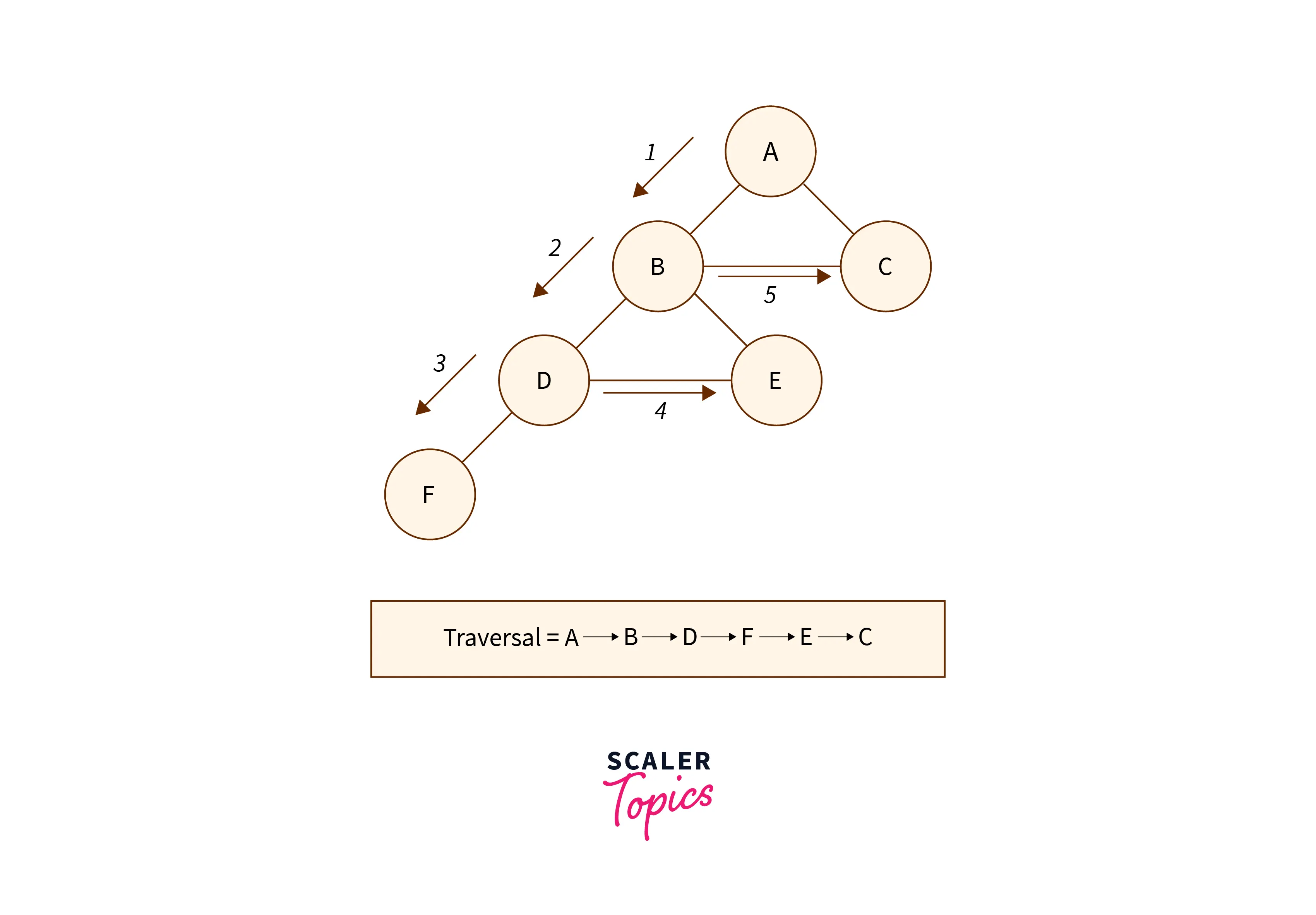
Depth First Search (DFS)
Depth-first search (DFS) is a graph traversal algorithm that explores as far as possible along each branch before backtracking. It employs a stack data structure to maintain a path and explores as deeply as possible before backtracking. DFS is often used in topological sorting, solving maze problems, and detecting cycles in graphs due to its exhaustive nature.
Algorithm of DFS
- Begin by placing a vertex from the graph at the top of the stack.
- Extract the top item from the stack and mark it as visited.
- Generate a list of adjacent nodes for the current vertex and add them to the top of the stack if they haven’t been visited yet.
- Keep iterating over steps 2 and 3 until the stack has been fully emptied.
Pseudocode of Depth First Search Algorithm
Create a stack (say S)
Mark the initial Vertex V => Visited.
Push V onto the stack-S
WHILE stack-S is not empty:
Pop an element from the front of stack-S
Store that element in Vertex (say U)
Loop over all the Unvisited Neighbors of Vertex-U
Mark the neighbor as Visited
Push the Neighbor to the S.
Applications of DFS
- Locating any route between the graph’s vertices u and v.
- Determining how many connected elements are present in an undirected graph.
- Sorting a given directed graph topologically.
- Finding components with strong connections in the directed graph.
- In the given graph to find cycles or to determine whether the provided graph is bipartite.
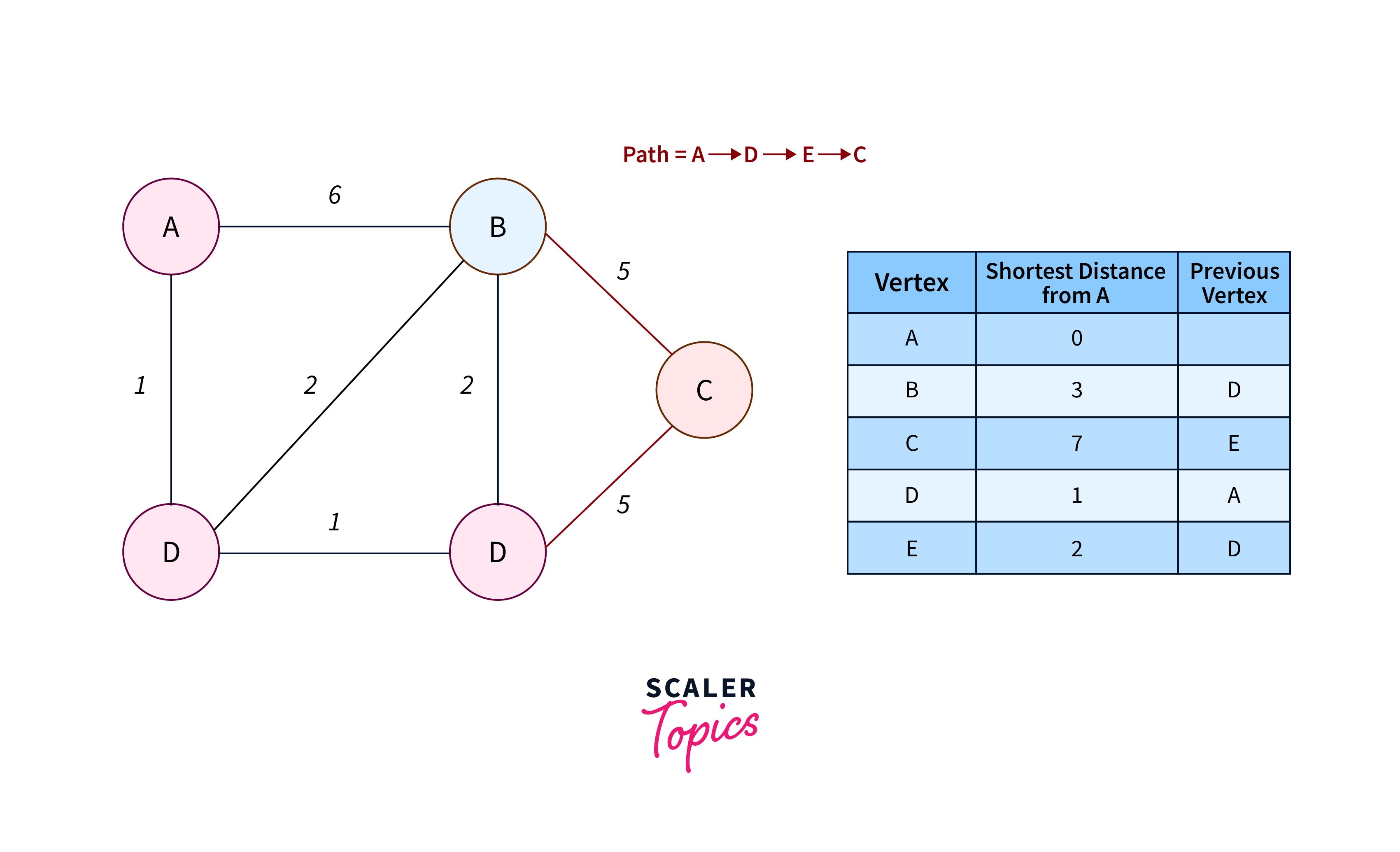
Dijkstra’s Shortest Path Algorithm
Dijkstra’s algorithm is a graph search algorithm used to find the shortest path between nodes in a weighted graph. It operates by iteratively selecting the node with the shortest distance from a source node and updating the distances to its neighboring nodes accordingly. Dijkstra’s algorithm is widely used in various applications such as routing protocols in computer networks and navigation systems in transportation.
Algorithm of Dijkstra’s
- Initialize all vertices to infinity, except the source vertex.
- Push the source vertex into a priority queue in the format (distance, vertex), setting its distance to 0.
- Extract the vertex with the minimum distance from the priority queue.
- Update distances after extracting the minimum distant vertex by considering the condition (current vertex distance + edge weight < next vertex distance).
- If a visited vertex is extracted, proceed to the next iteration without utilizing it.
- Continue steps 3 to 5 until the priority queue becomes empty.
Pseudocode of Dijkstra’s Algorithm
function Dijkstra(Graph, source):
for each vertex v in Graph:
distance[v] = infinity
distance[source] = 0
G = the set of all nodes of the Graph
while G is non-empty:
Q = node in G with the least dist[ ]
mark Q visited
for each neighbor N of Q:
alt_dist = distance[Q] + dist_between(Q, N)
if alt-dist < distance[N]
distance[N] := alt_dist
return distance[ ]
Applications of Dijkstra’s Algorithm
- Navigation Apps: Dijkstra’s algorithm powers mapping services like Google Maps, offering optimal travel routes between locations.
- Networking: Essential for determining minimum-delay paths in computer networks and telecommunications.
- Game Strategies: Utilized in game-playing algorithms to make strategic moves and reach specific objectives efficiently.
- Route Optimization: Key in logistics for optimizing delivery routes, public transport systems, and supply chain management.
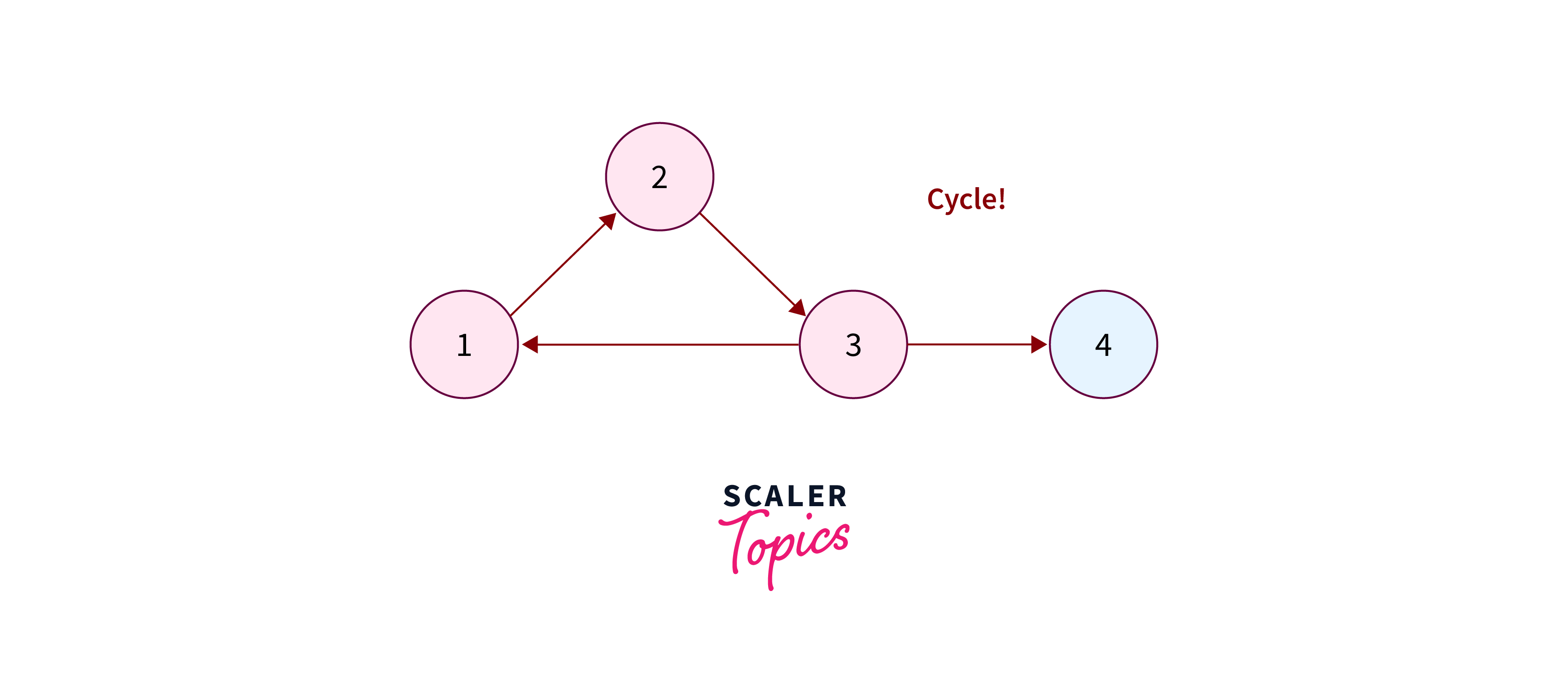
Cycle Detection
In the context of graph algorithms, a cycle is defined as a path that both starts and ends at the same vertex. This means that if you follow a path from a vertex and return to the starting point, you’ve encountered a cycle. Cycle detection involves identifying such loops or chains that include all the nodes visited during traversal. Hence, the essence of cycle detection lies in recognizing and handling these recurring patterns within the graph structure.
Pseudocode of Cycle Detection Algorithm
Initialize an array visited VARR
Create a stack (say S)
Add the initial Vertex V in VARR.
Push V onto the stack-S
WHILE stack-S is not empty and all Vertices have been marked:
Pop an element from the front of stack-S
Store that element in Vertex (say U)
If Vertex-U is already in VARR
then a cycle is found
return as cycle is found
Else:
Loop over all the Unvisited Neighbors of Vertex-U
Add the neighbor to VARR
Push the Neighbor to the S.
Applications of Cycle Detection
Cyclic algorithms are utilized in:
- Message-Based Distributed Systems: Facilitating routing and fault tolerance.
- Large-Scale Cluster Processing Systems: Optimizing data processing and resource allocation.
- Deadlock Detection: Ensuring smooth operation in concurrent systems.
- Cryptographic Applications: Managing encrypted messages and keys for secure communication.
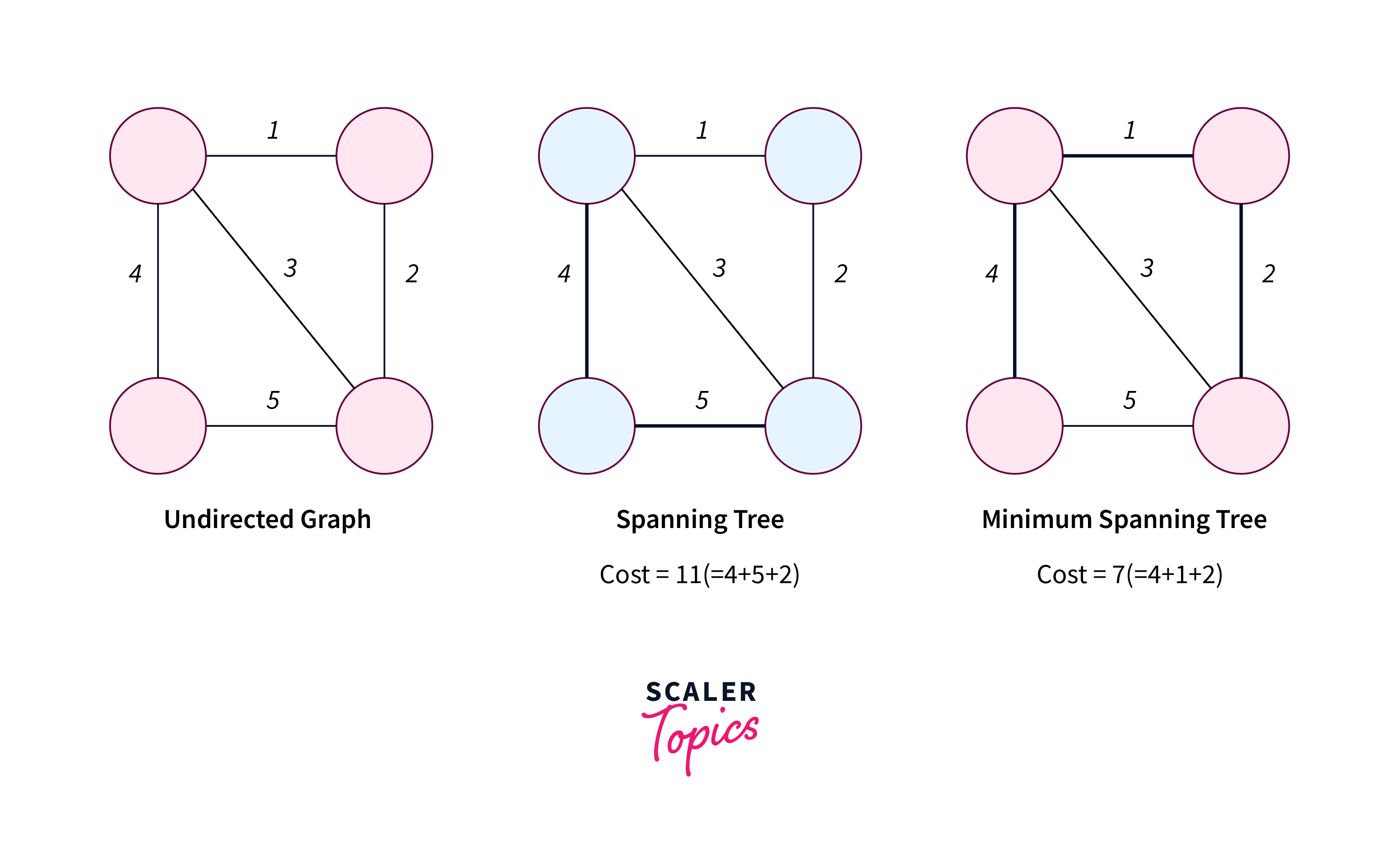
Minimum Spanning Tree
A minimum spanning tree (MST) is a subset of edges in a graph that connects all vertices without forming cycles and minimizes the total edge weight. It ensures optimal connectivity while minimizing the sum of edge weights. Multiple MSTs can exist depending on edge weights and connectivity criteria.
Pseudocode of Minimum Spanning Tree
// Initialize ReachSet with the starting vertex
ReachSet = {0};
// Initialize UnReachSet with all other vertices
UnReachSet = {1, 2, ..., N-1};
// Initialize SpanningTree as empty
SpanningTree = {};
// Iterate until UnReachSet is empty
while ( UnReachSet is not empty )
{
// Find edge e = (x, y) with smallest cost
// such that x is in ReachSet and y is in UnReachSet
e = findEdgeWithSmallestCost(ReachSet, UnReachSet);
// Add edge e to SpanningTree
SpanningTree = SpanningTree + {e};
// Add vertex y to ReachSet
ReachSet = ReachSet + {y};
// Remove vertex y from UnReachSet
UnReachSet = UnReachSet - {y};
}
Applications of Minimum Spanning Tree
- Network Design: MST is crucial for designing efficient network connections in graph algorithms.
- Traveling Salesman Problems: MST plays a role in optimizing routes for the traveling salesman problem.
- Minimum-Cost Weighted Perfect Matching: Useful for finding the minimum-cost matching in graph theory.
- Multi-Terminal Minimum Cut Problems: Applied to solve problems related to cutting a graph into subgraphs.
- Image and Handwriting Recognition: MST aids in analyzing patterns and structures in images and handwriting.
- Cluster Analysis: MST assists in grouping data points into clusters for analysis and interpretation.
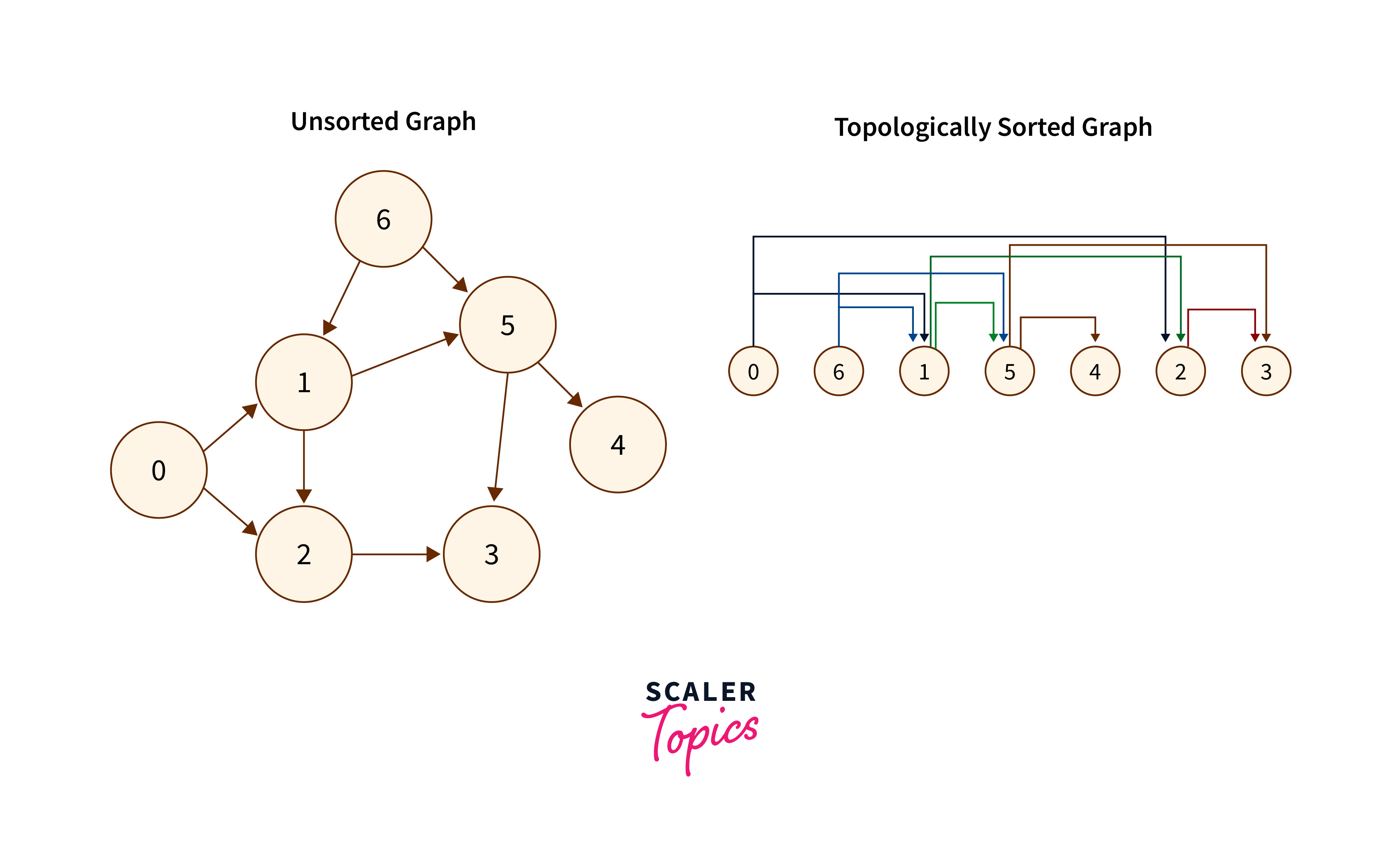
Topological Sorting
Topological sorting is a method used to arrange the vertices of a directed graph in a linear order. This ensures that for every directed edge from vertex A to vertex B, A precedes B in the ordering. This ordering aids in understanding dependencies and sequences in the graph structure.
Pseudocode of Topological Sorting
function topologicalSort(graph):
// Initialize an empty list to store the sorted vertices
sortedVertices = []
// Initialize a set to keep track of visited vertices
visited = {}
// Perform DFS traversal on each vertex
for each vertex v in graph:
if v is not visited:
DFS(graph, v, visited, sortedVertices)
// Reverse the sorted vertices list to obtain the topological order
reverse(sortedVertices)
return sortedVertices
function DFS(graph, vertex, visited, sortedVertices):
// Mark the current vertex as visited
visited[vertex] = true
// Traverse all adjacent vertices
for each adjacent vertex w of vertex:
if w is not visited:
DFS(graph, w, visited, sortedVertices)
// Add the current vertex to the sorted list
sortedVertices.append(vertex)
Applications of Topological Sorting
- Kahn’s Algorithm: Utilizes topological sorting to efficiently sort vertices by processing nodes with no incoming edges first.
- DFS Algorithm: Applies Depth-First Search to explore and order vertices, ensuring dependencies are satisfied in the resulting sequence.
- Scheduling: Utilized in task or instruction scheduling to ensure that dependent tasks are executed in the appropriate sequence.
- Dependency Resolution: Valuable in resolving dependencies in software development, determining the order in which components should be compiled or linked to fulfill dependencies accurately.
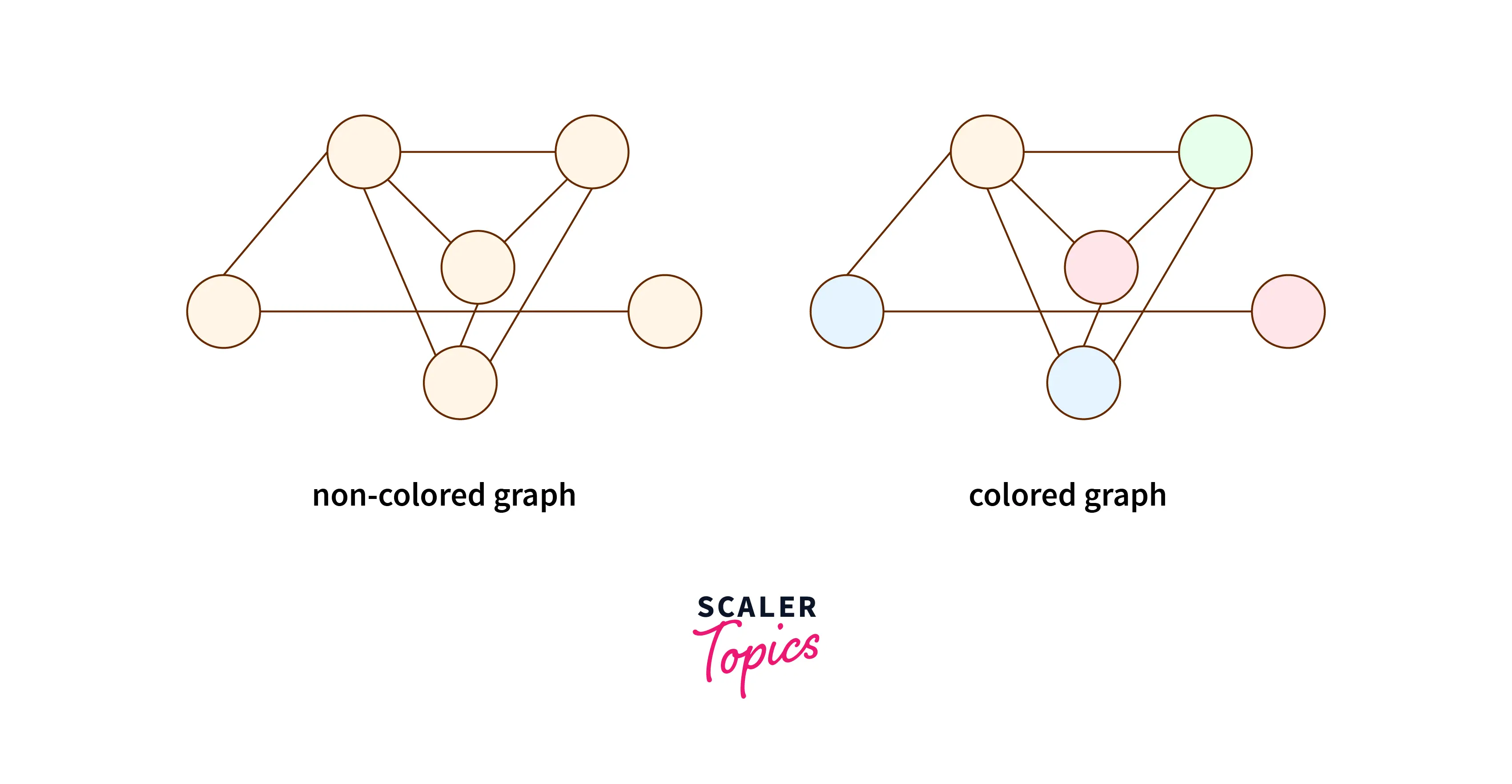
Graph Coloring
The task of “coloring” a graph’s components entails doing so while adhering to a number of limitations and constraints. In other terms, “graph coloring” is the act of giving vertices colors so that no two neighboring vertexes have the same hue.
Chromatic Number: The chromatic number of a graph G represents the minimum number of colors needed to properly color it.
Pseudocode of Graph Coloring
create the processors P(i0,i1,...in-1)
where 0_iv < m, 0 _ v < n
declare status[i0,..in-1] = 1
for j varies from 0 to n-1 do
for k varies from 0 to n-1 do
if aj, k=1 and ij=ik then
status[i0,..in-1] =0
ok = sum(Status)
if ok > 0, then
display valid coloring exists
else
display invalid coloring
Applications Graph Coloring
The idea of graph coloring is used in the creation of schedules, Suduku, registration allocation, and the coloring of maps.
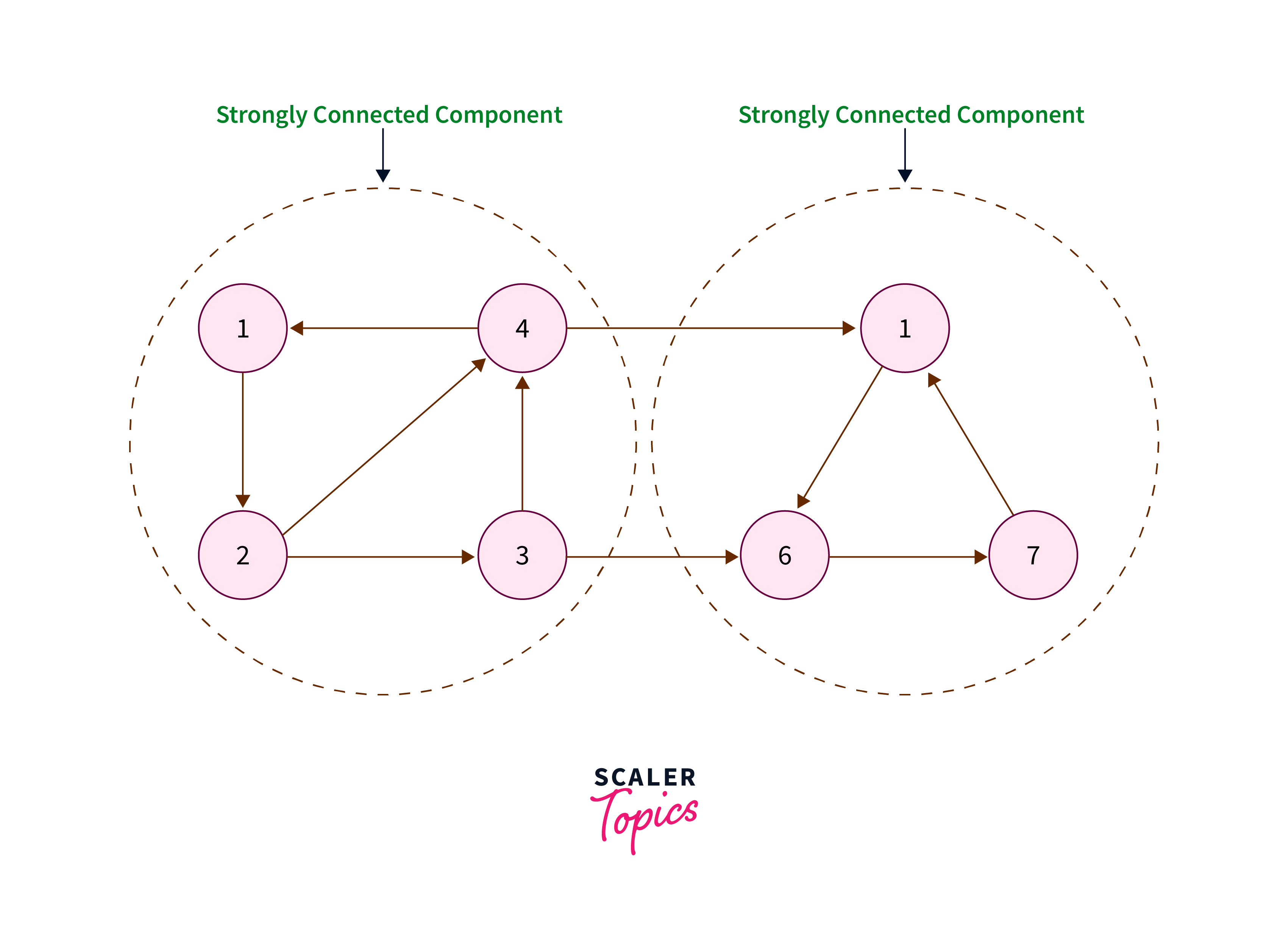
Strongly Connected Components
Strongly connected components (SCCs) are subsets of vertices in a directed graph where each vertex is reachable from every other vertex within the subset. Identifying SCCs is essential for understanding the connectivity and structure of directed graphs, aiding in various applications such as network analysis and software engineering.
Pseudocode of Strongly Connected Components
function DFS(graph, vertex, visited, stack)
visited[vertex] = true
for each neighbor in graph[vertex]:
if not visited[neighbor]:
DFS(graph, neighbor, visited, stack)
stack.push(vertex)
function Transpose(graph)
Create an empty transposed graph
for each vertex in graph:
for each neighbor in graph[vertex]:
add vertex to the neighbors of neighbor in the transposed graph
return transposed graph
function DFS_SCC(graph, vertex, visited, component)
visited[vertex] = true
component.add(vertex)
for each neighbor in graph[vertex]:
if not visited[neighbor]:
DFS_SCC(graph, neighbor, visited, component)
function Kosaraju(graph)
Initialize an empty stack
Create an array to keep track of visited vertices, initialized to false
for each vertex in graph:
if not visited[vertex]:
DFS(graph, vertex, visited, stack)
Create the transpose of the graph
Reset visited array to all false
Initialize an empty list to store SCCs
while stack is not empty:
vertex = stack.pop()
if not visited[vertex]:
Create a new empty set for the component
DFS_SCC(transposed graph, vertex, visited, component)
Add component to the list of SCCs
return list of SCCs
Applications of Strongly Connected Components
- Network Analysis: SCCs help in understanding the connectivity and flow within directed networks, crucial for optimizing communication and resource allocation.
- Software Engineering: Used in analyzing dependencies between modules or components, aiding in code refactoring and system design.
- Routing Algorithms: SCCs play a role in designing efficient routing algorithms for directed networks, ensuring optimal data transmission paths.
- Database Management: Utilized in database systems for query optimization and transaction management, improving performance and data integrity.
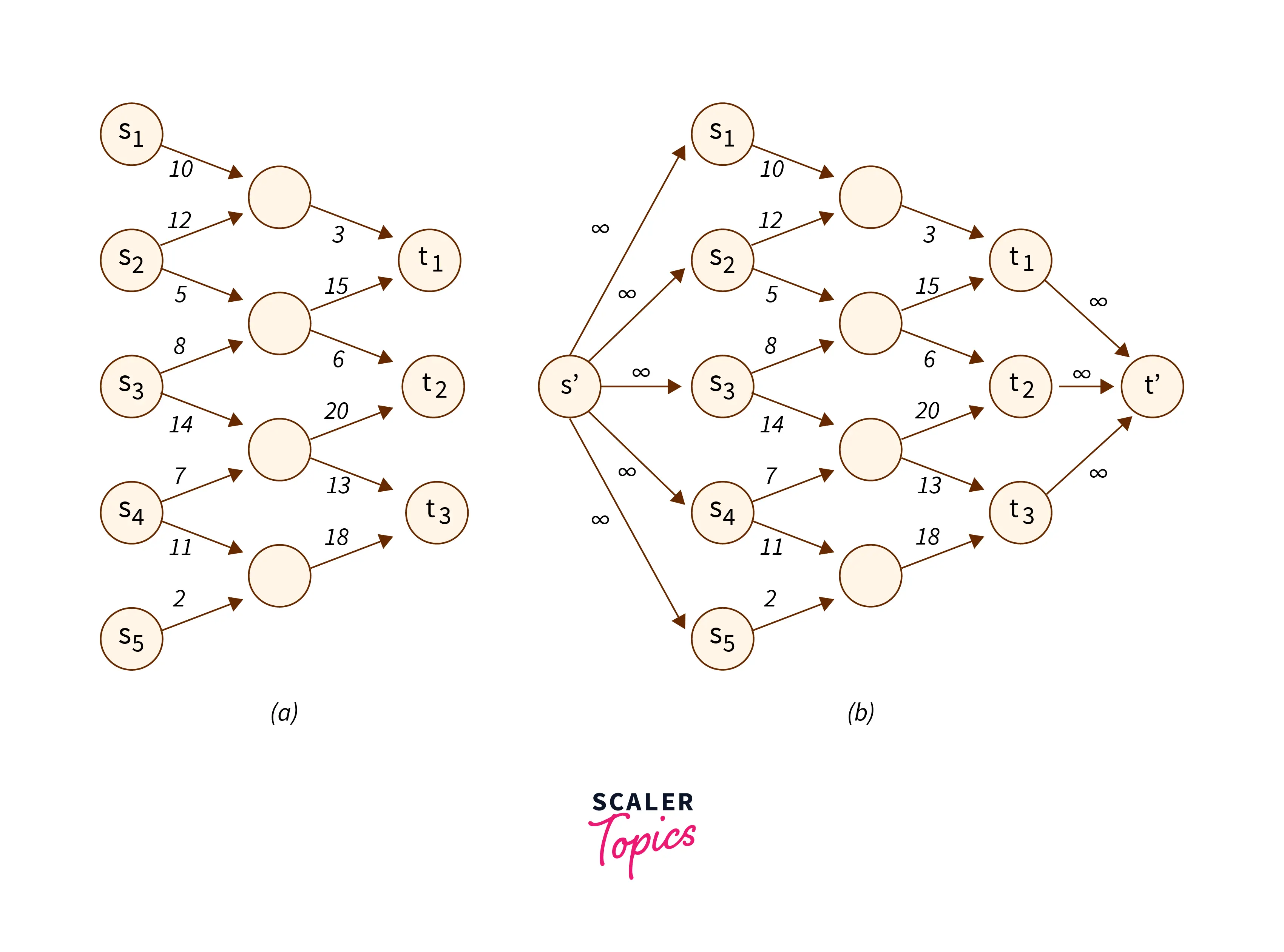
Maximum Flow
When used as a problem-solving method, the maximum flow algorithm often models the graph after a network flow architecture. As a result, the method for calculating the maximum flow is to identify the flow channel with the highest flow rate. The maximum flow rate is calculated using augmenting routes, where the flow in the sink node equals the total flow based out of the source node.
Pseudocode of Maximum Flow Algorithm
MaximumFlow(Graph Gr, Node N, Node M):
Initialize flow in all edges to 0, FLO = 0
Construct level graph
while (there exists an augmenting path in the level graph):
find blocking flow fl in the level graph
FFMAX = FLO + fl
Update level graph
return FLO
Applications of Maximum Flow Algorithm
- Maximum Flow Algorithms: Ford-Fulkerson, Edmonds-Karp, and Dinic’s algorithms are used to solve the maximum flow problem efficiently.
- Flight Crew Scheduling: Helps optimize crew assignments for flights, ensuring efficient coverage and resource allocation.
- Image Segmentation: Utilized in image processing to distinguish foreground and background regions by analyzing flow between pixels or regions.
- Sports Strategy: Applied in sports like basketball to strategize and maximize scores, aiding teams in achieving competitive advantage.
Matching
The edges of a matching algorithm or approach in a graph are those that share absolutely no vertices. When the greatest number of edges and the greatest number of vertices match, the matching is said to be maximum matching. It employs a particular methodology to identify entire matches, as seen in the graphic below.
Pseudocode of Matching Algorithm
Declare Graph Gr, initial matching M on G
FindMatching(Gr, Match)
Path ← FindPath(Gr, Match)
if P is non-empty then
return find_maximum_matching(Gr, augment Match along Path )
else
return Match
FindPath(Gr, Match)
Forest ← empty forest
unmark all vertices and edges in Gr, mark all edges of Match
for each exposed vertex v do
create a singleton tree { v } and add the tree to Forest
while there is an unmarked vertex v in Forest with distance(v, root(v)) even do
while there exists an unmarked edge e = { v, w } do
if w is not in Forest then
x ← vertex matched to w in Match
add edges { v, w } and { w, x } to the tree of v
else
if distance(w, root(w)) is odd then
no operation
else
if root(v) ≠ root(w) then
Path ← path (root(v) → ... → v) → (w → ... → root(w))
return Path
else
B ← blossom formed by e and edges on the path v → w in T
Gr’, Match’ ← contract Gr and Match by B
Path’ ← FindPath(Gr’, Match’)
Path ← lift Path’ to Gr
return Path
mark edge e
mark vertex v
return empty path
Application of Matching Algorithm
- Blossom and Hopcroft-Karp Algorithms: Efficiently solve matching problems in graphs.
- Hungarian Method: Resolves optimization problems using matching principles.
- Stable Marriage Problem: Matches couples based on preferences, ensuring stability.
- Resource Allocation: Allocates resources efficiently, optimizing utilization.
Explore Scaler Topics Data Structures Tutorial and enhance your DSA skills with Reading Tracks and Challenges.
Conclusion
- Vital for Analysis: Graph algorithms are crucial for analyzing interconnected data structures, enabling tasks like pathfinding and connectivity analysis.
- Broad Applications: From route optimization to recommendation engines, they drive insights and optimizations across various domains.
- Relevant in Modern Computing: The relevance of graph algorithms extends to fields like bioinformatics and logistics, showcasing their importance in modern computing.
- Efficient Solutions: Graph Algorithms like BFS, DFS, Dijkstra’s, and MST offer efficient solutions for various graph-related problems.
- Optimization and Efficiency: They optimize network design, routing, and resource allocation, enhancing system efficiency.
- Versatile Applications: Used in navigation apps, network analysis, game strategies, and scheduling, highlighting their versatility.