Geometric Progression

Geometric Progression (GP) is a sequence where each term results from multiplying the previous one by a constant, known as the Common Ratio. Consider folding a paper multiple times: while it’s folded 4-5 times, determining its final stack height illustrates GP principles. This progression concept offers insights into patterns formed by consistent multiplicative growth.

Notation

Lets deep dive into geometric progression and understand the various terminologies used in it.

1. First Term: Each number of the series is called a “term”. Hence, the number from which the series starts is called the First Term. It is generally denoted by $a$. In our previous example, the first term is $1$.
2. Common ratio: The non-zero constant from which we were multiplying each of the terms is called the common ratio. It is generally denoted by $r$. In our previous example, this ratio is $2$.

General Form

Lets see the sequence again,

$\color{blue} 1,\ 2,\ 4,\ 8,\ 16,\ 32,\ 64\ …$
$\implies \color{blue}1,\ \color{blue}1\times 2, \color{blue}1 \times (2\times 2),\ 1\times (2\times 2\times 2),\ 1\times (2\times 2\times 2\times 2),\ \color{blue}1\times (2\times 2\times 2\times 2\times 2),\ \color{blue}1\times (2\times 2\times 2\times 2\times 2\times 2),\ …$
$\implies \color{blue}1,\ \color{blue}1\times 2^1,\ \color{blue}1\times 2^2,\ \color{blue}1\times 2^3,\ \color{blue}1\times 2^4, \ \color{blue}1\times 2^5,\ \color{blue}1\times 2^6\ …$

Let $\color{blue}{a=1}$ and $r=2$,

$\implies \color{blue}a,\ \color{blue}a \times r^1,\ \color{blue}a\times r^2,\ \color{blue}a\times r^3,\ \color{blue}a\times r^4, \ \color{blue}a\times r^5,\ \color{blue}a\times r^6\ …$

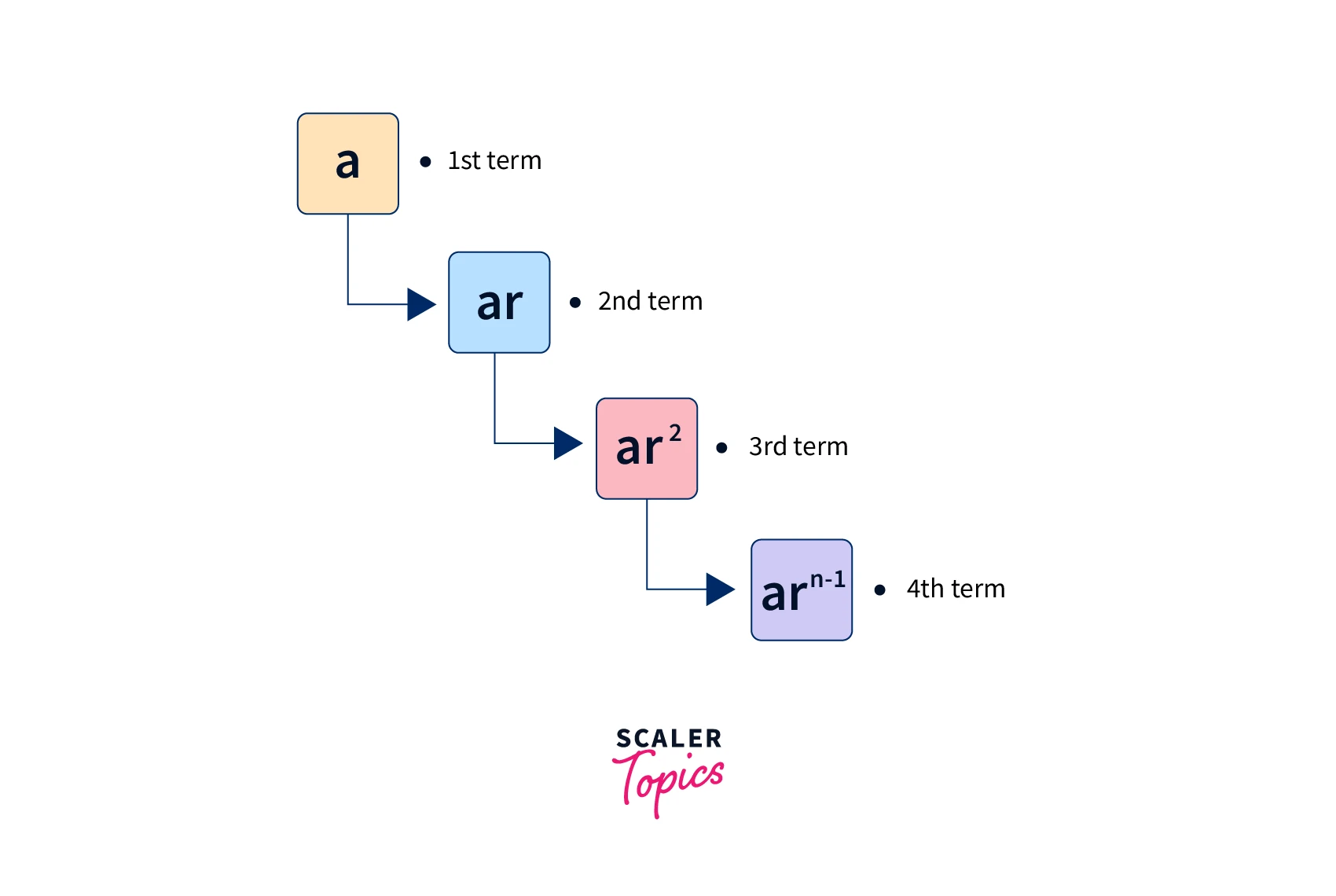
Hence we say, in general, geometric progression is of the form $a, ar, ar^2, ar^3, ar^4,…, ar^{n-1}$

where,

$a =$ First term

$r =$ common ratio

$ar^{n-1} =$ nth term

Nth Term

Intuition

When we write the formula for the nth term of the GP series, we try to generalize the last term of a finite GP in terms of the first term and the common ratio of the GP.

Derivation

Let $a$ be the first term and $r$ be the common ratio for a Geometric Sequence.

Then, the second term, $a_2 = a \times r = ar$

Third term, $a_3 = a_2 \times r = ar \times r = ar^2$

Similarly, nth term, $a_n = ar^{n-1}$

Note: The nth term is the last term of finite GP.

Formula

The formula to find the nth term of GP is:

$a_n = ar^{n-1}$

We use “n-1” because $ar_0$ is for the 1st term and $r_0$ is 1.

Example

Consider the following sequence,

$1, 2, 4, 8, 16, 32, 64\ …$

Here,
$a_1 = 1\times 2^0 =1$
$a_2 = 1\times 2^1 =2$
$a_3 = 1\times 2^2 =4$
$a_3 = 1\times 2^3 =8$
$a_4 = 1\times 2^4 =16$
$a_5 = 1\times 2^5 =32$
$a_6 = 1\times 2^6 =64$
and so on.

Types of GP

A geometric progression can be finite or infinite depending on the number of terms it contains. Let’s see a brief description about both of them.

Finite GP

• If the number of terms in a geometric progression is finite then it is called a finite GP.
• In general, we can write finite GP as $a, ar, ar^2, ar^3,…,ar^{n-1}$.
• For example, $1, 2, 4, 8, 16, 32, 64$ is a finite GP.

Infinite GP

• If the number of terms in a geometric progression is infinite then it is called an infinite GP.
• In general, we can write infinite GP as $a, ar, ar^2,…,ar^{n-1},…$.
• For example, $1, 2, 4, 8, 16, 32, 64,\ …$ is an infinite GP.

Sum of GP for Nth term

Intuition

As we have seen earlier, in a GP sequence every term can be expressed with the help of the first term($a$) and the common ratio($r$). Similarly we can express the sum of geometric progression in terms of $a$ and $r$.

Derivation

Let’s see how we can derive the formula for finite GP.

First, call the whole sum $S$:

$S = a + ar + ar^2 + … + ar^{n-2}+ ar^{n-1}$

Next, multiply $S$ by $r$:

$-S. r = ar + ar^2 + … + ar^{n-1} + ar^n$

Notice that $S$ and $S·r$ are similar?

Now subtract them!

$S = a + ar + ar^2 + … + ar^{n-2}+ ar^{n-1}$

$-S·r = ar + ar^2 + ar^3 + … + ar^{n-1} + ar^n$

$\implies S – S·r = a – ar^n$
$\implies S(1-r) = a(1 – r^n)$
$\implies S = a\frac{(1 – r^n)}{(1-r)}$

Formula

The formula for the sum of $n$ terms of a finite GP is given as:

$S = \sum_{k=0}^{n-1}(ar^k) = a\frac{(1 – r^n)}{(1-r)}$

When GP is infinite, i.e., $n \rightarrow \infty$

$S = \sum_{k=0}^{\infty}(ar^k) = a\frac{1
}{(1-r)}$

Conclusion

• In geometric progression(GP), each term is formed by multiplying the previous term by a non-zero constant (known as common ratio).
• The formula to find the nth term of GP is:
  $a_n = ar^{n-1}$
  where $a$ is the first term of the GP and $r$ is the common ratio of the GP.
• The formula for the sum of $n$ terms of a finite GP is given as:
  $S = \sum_{k=0}^{n-1}(ar^k) = a\frac{(1 – r^n)}{(1-r)}$
  where $a$ is the first term of the GP, $r$ is the common ratio of the GP and $k$ denotes the $k$th term of the GP.
• The formula for the sum of $n$ terms of an infinite GP, i.e., $n \rightarrow \infty$, is given as:
  $S = \sum_{k=0}^{\infty}(ar^k) = a\frac{1
  }{(1-r)}$
  where $a$ is the first term of the GP, $r$ is the common ratio of the GP and $k$ denotes the $k$th term of the GP.

XBO lamps are at high internal pressure when cold up to 35 bar or approximately psi and at operating temperature up to 80 bar or approximately psi at bulb wall temperatures of C to C. The go tool's usual package mechanism does not apply: package path elements like. Clutter is the term used and includes ground returns, sea returns, weather, buildings, birds and insects. It was revealed on Twitter that he was predicting that day he would get 1 most subscribed and would celebrate by sleeping, in which he did around 2 or 3 AM. AW Message Format AW: 'identifier' is referenced by another module but is not on the current module's export list. While the residents of the city were distracted by one of their great religious feast days, the Persian army waded the river and marched under the walls of Babylon unnoticed. Change : When you hold circle to quit, there is only one loading ring instead of 3. He was responsible for using an iron knife in the underworld to open the mouths of people who had recently died. The police raided the hall half way through their set in riot gear and a riot ensued. Therefore, the best way to implement it is like this. The s and 50s As early as the s, the Brill Building was home to a number of jazz and big band musicians, including Irving Mills. If we use the second, the intermediate page is different, but we do the same i. There is no pub or eating facilities in the village, but plenty of great places to eat nearby. Guest: cheap reebok shaqnosis retro black white for sale. A socket wrench used to turn lug nuts on automobile wheels. News Corp owns a 65 percent stake in the combined entity, with Telstra owning 35 percent. Service B includes an oil and filter change, a tire rotation and other maintenance checks. A pressurized heavy-water reactor PHWR is a nuclear reactor that uses heavy water deuterium oxide D 2 O as its coolant and neutron moderator. There should be no clots in implantation bleeding, and it can last anywhere from a few hours to a few days. Also, since it features 18 different levels of adjustment, you can always find your perfect arrangement depending on your height and preferences. I wanted to share them with you guys in case any of you were looking… Read More.