Sieve of Eratosthenes is an ancient algorithm of mathematics that is used to calculate prime numbers belonging to a certain range of positive integers. The Extended sieve is a modification to the standard Sieve algorithm using which one can calculate prime numbers present in a larger range of numbers efficiently.
Scope
- The issue with the standard sieve has been discussed and a solution to it has been explained.
- The concept of an extended version of Sieve of Eratosthenes has been discussed in detail with examples.
- The article contains codes of extended sieve in two popular languages $i.e.$
C/C++andJava.
Takeaways
Time complexity is the same as of standard sieve $i.e.$ $O(n\times\log{(\log n)})$
Introduction
Prime numbers are one of the most important concepts of mathematics. They find their use in a variety of applications, especially in cryptography. And if they are so important there must be a way to find prime numbers efficiently instead of performing a time-taking primality check.
Hence 2200 Years ago, Eratosthenes (A Greek mathematician) came up with an approach that is vastly used in calculating prime numbers in a range which is known as the Sieve of Eratosthenes or more commonly simply "Sieve".
What is Sieve of Eratosthenes
Sieve of Eratosthenes is an algorithm that is used to find prime numbers in the range $[1,n]$ for a given $n$. The basic idea behind Sieve is to initially assume all numbers from $2$ to $n$ as prime (as it is known that $1$ is not prime) and iterate from $i=2$ to $\sqrt{n}$ and if $i$ is marked as a prime number then mark all the multiples $i$ as non-primes (composite).
The algorithm is discussed in depth in our previous article Sieve of Eratosthenes, please go through it to understand it more clearly.
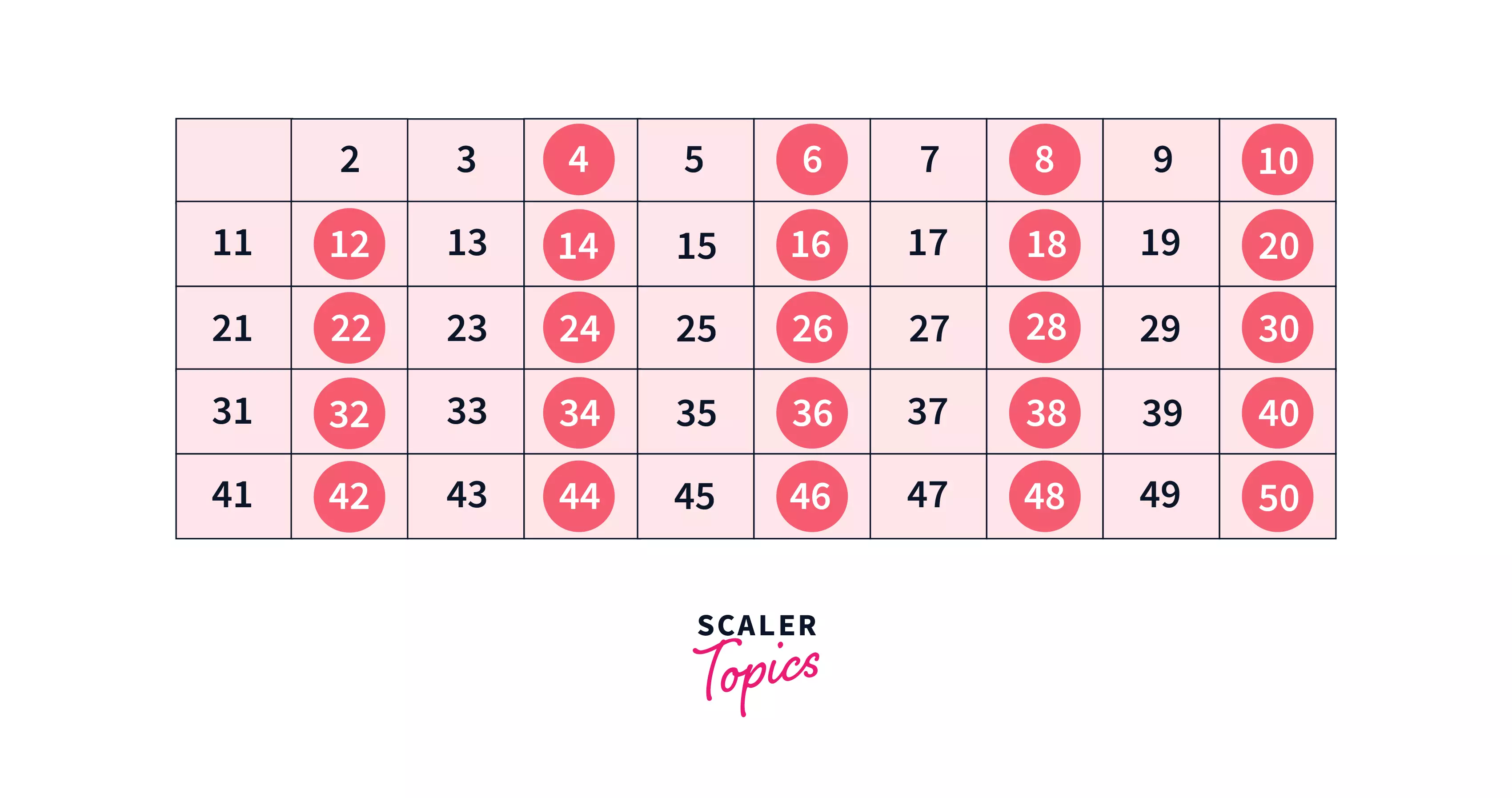
Problem with Sieve of Eratosthenes
The major and the only issue with the standard implementation of Sieve is, the extra $O(n)$ space (visited array) is needed to find all prime numbers in the range $[1,n]$. Imagine a situation, where we need to find all prime numbers in the range $[1,10^7]$ using the standard Sieve of Eratosthenes algorithm. It would not be an efficient approach as it is difficult to allocate $O(n)$ extra space when $n\geq 10^7$.
If somehow we can optimize space complexity then we can solve the issue. For that, we have a modified algorithm called “Extended Sieve of Eratosthenes”.
What is Extended Sieve of Eratosthenes?
The main idea behind the extended sieve is to divide the range of $[1,n]$ into many segments, and compute primes of each segment one by one. Now the question arises that how much should be the size of each segment. Generally, the size of each segment is taken around $\sqrt n$.
After which the segments will look like, $[1,\sqrt n],$ $[(\sqrt n +1), (2\times\sqrt n)],$ $…,$ and $[(n-\sqrt n), n]$.
For Example:
Let’s assume $n$ to be $16$ then we will not find prime numbers in the range $[1,16]$. Instead we will find primes in the segments – $[1,4],$ $[5, 8],$ $[9,12]$, and $[13,16]$ individually.
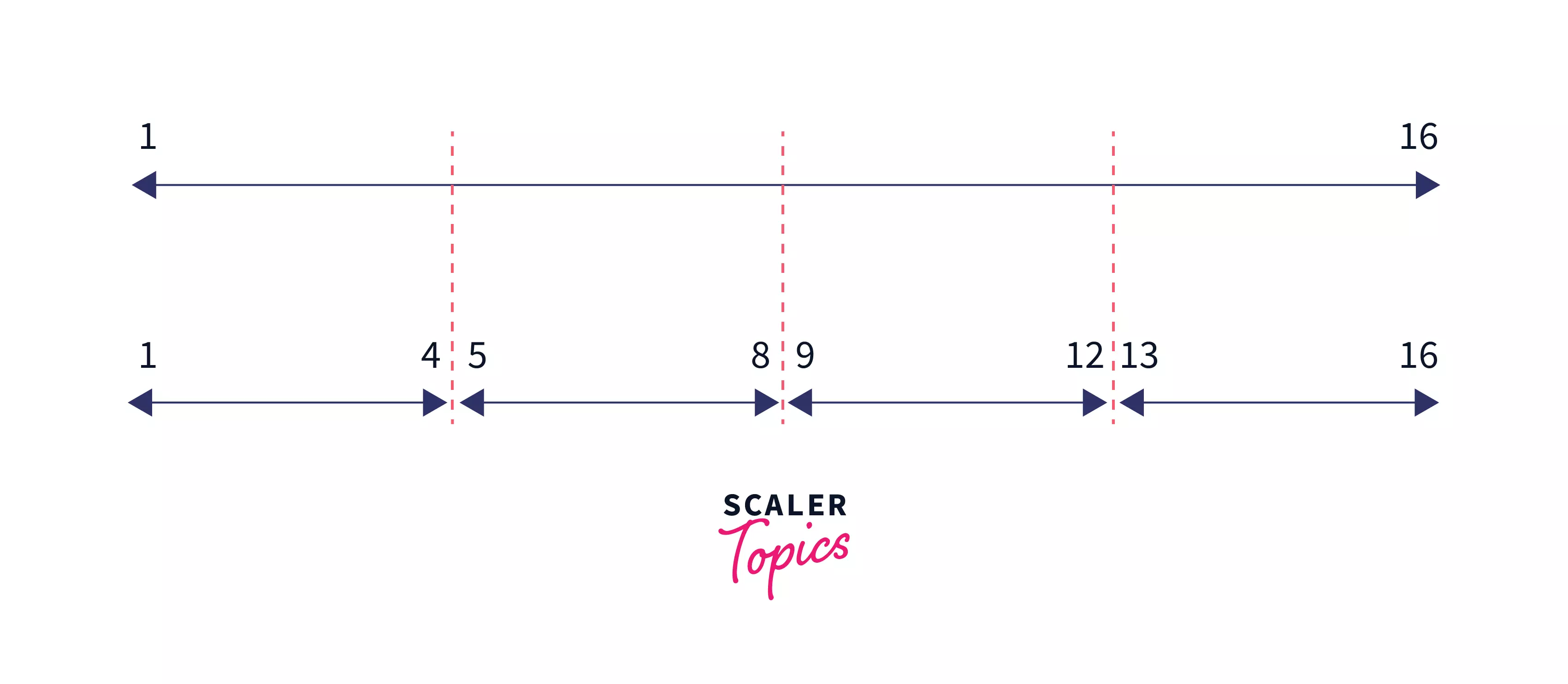
Below are the steps for implementing the extended sieve of Eratosthenes:
- Divide the range $[1,n]$ into segments of size at most $\sqrt n$.
- Use the standard sieve to find prime numbers up to $\sqrt n$ and store them in an array/list
prime. - Do the following for each segment $[low, high]$
- Create a boolean
visitedarray of size $high-low+1$ and mark all its entries to be true. - Iterate through all the prime numbers stored in the list
primeand mark all its multiples as false that lies in the range $[low, high]$.
- Create a boolean
We are doing the third step because we want to find the prime numbers belonging to a range $[\sqrt{n}+1, 2\times\sqrt n],$ $[(2\times\sqrt{n})+1, 3\times\sqrt n]$ and so on. By performing the third step it can be done easily.
Example of Extended Sieve
Let’s say we want to find all prime numbers less than or equal to 50 using the extended Sieve algorithm as discussed above.
- Firstly we will divide the range of $[1,50]$ into some segments of size $\lfloor \sqrt{n}+1\rfloor$. We know that $\sqrt{50}=7.07$ and hence $\lfloor \sqrt{n}+1\rfloor=8$. So the segments will be like –
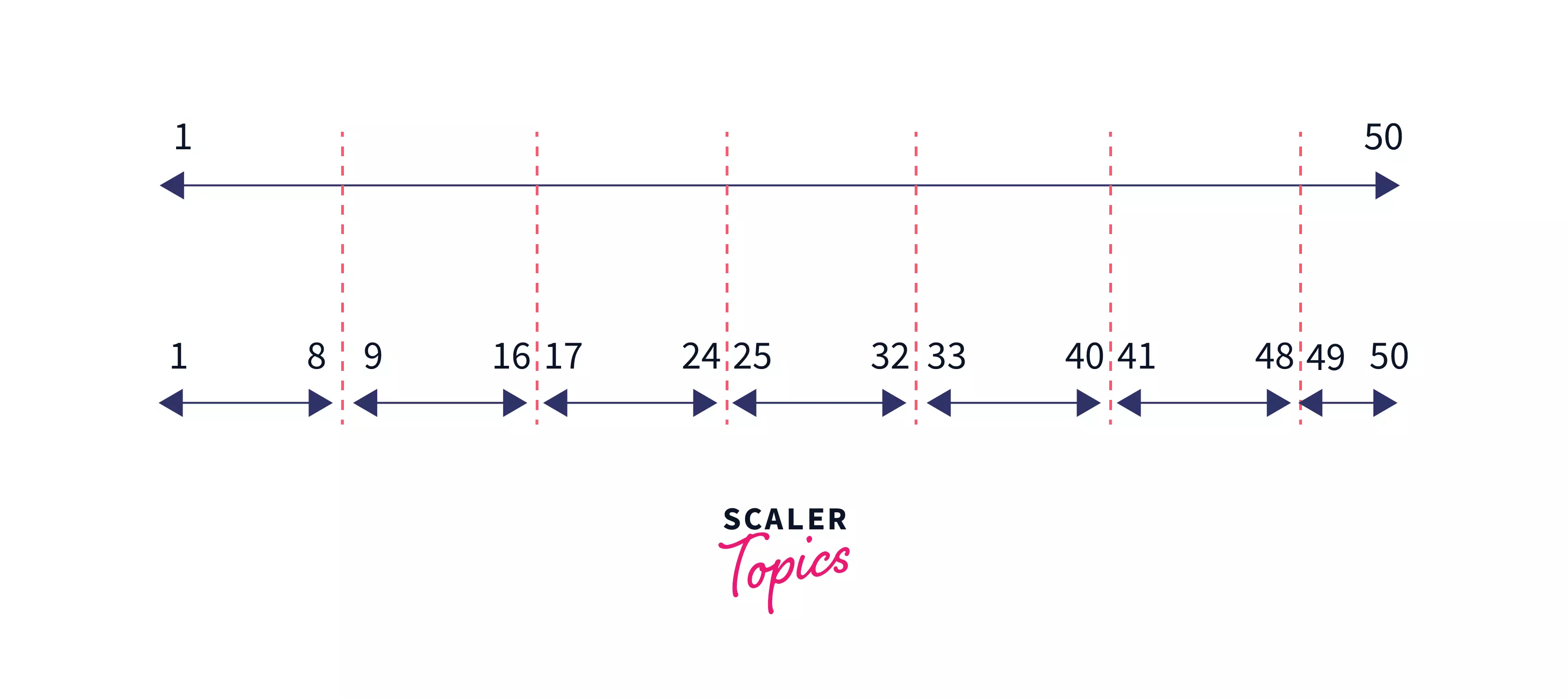
- Now using the Standard sieve we will find and print all prime numbers in the range $[1,8]$ and store them in list
prime. After performing we will have –prime=[2,3,5,7] - For segment $[9,16]$, we will make a boolean array
visitedand mark all elements as true (For easier representation we consider strikethrough numbers as false otherwise true).
Now we will check for multiples of all numbers inprime(say $x$) that lie in the range $[9,16]$ and mark them false. After which boolean array will look like –visited=9,10, 11,12, 13,14,15,16.
Now we will print and add all the un-marked numbers inprime, because they are not divisible by any number present inprimeand hence they are prime numbers. - Similarly for the segment $[17, 24]$, we will have –
visited= 17,18, 19,20,21,22, 23,24.
Again, due to the same reason we will print and add 17, 19, and 23 inprimes. - Perform the same procedure for all the other segments, at last, we will have the following elements printed on the user console and in the list.
prime=2 3 5 7 11 13 17 19 23 29 31 37 41 43 47
Implementation of Extended Sieve
Let’s say we want to find the prime numbers in the range $[1,n]$ using the extended sieve.
- The first step would be finding the size of segments in which we divide the problem. In general practice, $size$ is taken as $\lfloor \sqrt{n}\rfloor+1$.
- Then we would declare a list (say
prime) which would store all the prime numbers of the range $[1,size]$. - Now, we will run the classical sieve algorithm for the range $[1, size]$.
- Then we will define our next interval using $low$ as $size+1$ and $high$ as $2\times size$.
- Mark all the multiples of numbers in
primebelonging to the range $[low, high]$ as non-primes(composite). - Add $size$ to low and high and repeat the above steps till $low<n$.
Pseudocode:
function ExtendedSieve(n):
// Find size of segment i.e. sqrt(n)+1.
siz = sqrt(n) + 1
// 'Prime' list will store all the prime numbers.
prime=[]
// Call standard Sieve Function.
StandardSieve(prime, size)
// Print numbers stored in 'prime'
For(x in prime):
Print(x)
// Set low and high pointer
// as size and 2*size.
low = size + 1
high = 2 * size
// Iterate while low pointer
// is less than n.
While(low<n):
// If high exceeds n, limit
// it to n.
If(high>n):
high = n
// Create visited array of size (size+1),
// and mark all its entries as true.
visited[size+1]
For(i=0 To size):
visited[i]=True;
For(x in prime):
// Find minimum element is range [low, high]
// which is multiple of x.
lower=(low/x)*x
If(lower<low):
lower= lower + x
// Mark all its multiple as false
// i.e. Composite numbers (non-primes).
For(i=lower To i=high):
visited[i-low]=False
// Print all the prime numbers
// of the range [low, high].
For(i=low To high):
If(visited[i-low]):
Print(i)
// Increase low and high
// with size of the segment.
low = low + size
high = high + size
C/C++ implementation of Extended Sieve
// C++ program for Extended Sieve
// of Eratosthenes
# include<bits/stdc++.h>
using namespace std;
// Standard Sieve Function
void Sieve(vector<int> &prime, int n){
// Create a boolean visited array of size
// n+1 and mark all it's entries as true
// initially. At last if visited[i] is true
// then i is prime otherwise not.
bool visited[n+1];
for(int i=0;i<=n;i++)
visited[i]=true;
// Iterate from p=2 to
// p*p<=n (or p<=sqrt(n))
for(int p=2;p*p<=n;p++){
// If visited[p] is true, mark
// all it's multiple as false (non-prime).
if(visited[p]){
for(int i=p*p;i<=n;i+=p)
visited[i]=false;
}
}
// Iterate from p=2 to n, and
// if visited[p] is true it means
// it is prime. Add it in List and
// print it.
for(int p=2;p<=n;p++)
if(visited[p]){
prime.push_back(p);
cout<<p<<" ";
}
}
void extendedSieve(int n){
// Find size of segment i.e. sqrt(n).
int size=(int)(sqrt(n))+1;
// This list will store all the prime numbers.
vector<int> prime;
// Call standard Sieve Function.
Sieve(prime, size);
// Set low and high pointer
// as size and 2*size.
int low=size+1;
int high=2*size;
// Iterate while low pointer
// is less than n.
while(low<n){
// If high exceeds n, limit
// it to n.
if(high>n)
high=n;
// Create visited array of size (size+1),
// and mark all its entries as true.
bool visited[size+1];
for(int i=0;i<=size;i++)
visited[i]=true;
// Iterate for numbers in list "prime".
for(auto& x:prime){
// Find minimum element is range [low, high]
// which is multiple of x.
int lower=((int)(low/x)*x);
if(lower<low)
lower+=x;
// Mark all its multiple as false
// i.e. Composite numbers (non-primes).
for(int i=lower;i<=high;i+=x)
visited[i-low]=false;
}
// Print all the prime numbers
// of the range [low, high].
for(int i=low;i<=high;i++){
if(visited[i-low])
cout<<i<<" ";
}
// Increase low and high
// with size of the segment.
low+=size;
high+=size;
}
}
// Main function
int main(){
// n=50 means, we will be finding
// primes less than or equal to 50.
int n=50;
cout<<"Prime numbers smaller or equal to than 50 are -"<<endl;
// Call Extended Sieve function.
extendedSieve(n);
return 0;
}
Java implementation of Extended Sieve
// Java program for Extended Sieve
// of Eratosthenes
import java.util.*;
public class Main{
// Standard Sieve Function
private static void Sieve(List<Integer> prime, int n){
// Create a boolean visited array of size
// n+1 and mark all it's entries as true
// initially. At last if visited[i] is true
// then i is prime otherwise not.
boolean visited[]=new boolean[n+1];
for(int i=0;i<=n;i++)
visited[i]=true;
// Iterate from p=2 to
// p*p<=n (or p<=sqrt(n))
for(int p=2;p*p<=n;p++){
// If visited[p] is true, mark
// all it's multiple as false (non-prime).
if(visited[p]){
for(int i=p*p;i<=n;i+=p)
visited[i]=false;
}
}
// Iterate from p=2 to n, and
// if visited[p] is true it means
// it is prime. Add it in List and
// print it.
for(int p=2;p<=n;p++)
if(visited[p]){
prime.add(p);
System.out.print(p+" ");
}
}
private static void extendedSieve(int n){
// Find size of segment i.e. sqrt(n).
int size=(int)(Math.sqrt(n))+1;
// This list will store all the prime numbers.
List<Integer> prime=new ArrayList<>();
// Call standard Sieve Function.
Sieve(prime, size);
// Set low and high pointer
// as size and 2*size.
int low=size+1;
int high=2*size;
// Iterate while low pointer
// is less than n.
while(low<n){
// If high exceeds n, limit
// it to n.
if(high>n)
high=n;
// Create visited array of size (size+1),
// and mark all its entries as true.
boolean visited[]=new boolean[size+1];
for(int i=0;i<=size;i++)
visited[i]=true;
// Iterate for numbers in list "prime".
for(int x:prime){
// Find minimum element is range [low, high]
// which is multiple of x.
int lower=((int)(low/x)*x);
if(lower<low)
lower+=x;
// Mark all its multiple as false
// i.e. Composite numbers (non-primes).
for(int i=lower;i<=high;i+=x)
visited[i-low]=false;
}
// Print all the prime numbers
// of the range [low, high].
for(int i=low;i<=high;i++){
if(visited[i-low])
System.out.print(i+" ");
}
// Increase low and high
// with size of the segment.
low+=size;
high+=size;
}
}
// Main function
public static void main(String args[]){
// n=50 means, we will be finding
// primes less than or equal to 50.
int n=50;
System.out.println("Prime numbers smaller or equal to than 50 are -");
// Call Extended Sieve function.
extendedSieve(n);
}
}
Output:
Prime numbers smaller than or equal to than 50 are
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47
Complexity Analysis
Time Complexity– Here we are using the standard sieve of Eratosthenes multiple times but for a smaller range of numbers. It does not affect the time complexity as we are dividing the range into some number of segments and solving each segment individually.
Hence the time complexity is the same as of standard sieve $i.e.$ $O(n\times\log{(\log n)})$. For the proof of time complexity please refer to Sieve of Eratosthenes.Space Complexity– We are using an auxiliary boolean array visited of length ($size+1$), where $size=\sqrt{n}$. Hence the space complexity is $O(\sqrt{n})$.
Conclusion
- The
extended sievecan calculate prime numbers for a large $n$ when compared to the standard sieve algorithm. - By dividing range into segments of size $\sqrt n$ the space complexity is reduced to $O(\sqrt{n})$
- The
time complexityof extended sieve is the same as standard sieve algorithm $i.e.$ $O(n\times \log{(\log{(n)})})$. - The sieve algorithm is used in number theory and very commonly in cryptography.