The dynamic programming algorithm tries to find the shortest way to a solution when solving a problem. It does this by going from the top down or the bottom up. The top-down method solves equations by breaking them into smaller ones and reusing the answers when needed. The bottom-up approach solves equations by breaking them up into smaller ones, then tries to solve the equation with the smallest mathematical value, and then works its way up to the equation with the biggest value.
Example
To understand Dynamic Programming more clearly, let us look at an example.
Suppose we want to reconstruct the Fibonacci Series. It is a series, which starts with 0 and 1, and each consecutive term is the sum of the previous two terms in the series.
So, the first few terms of the Fibonacci Series are: 0, 1, 1, 2, 3, 5, 8, and so on. It is very clear that to calculate each term after the first two terms, we will need the previous two terms of the series.
Let’s try to solve this problem using Recursion. The nth term can be calculated by adding its previous two terms. The base cases for the recursion will be the first two terms of the series which are 0 and 1. Hence, the recursive solution would be:
int fibonacciNumber(int n):
//Base Cases
if(n==0 or n==1):
return n
//Recursive Call
return fibonacciNumber(n-1) + fibonacciNumber(n-2)A recursion tree for the Fibonacci sequence
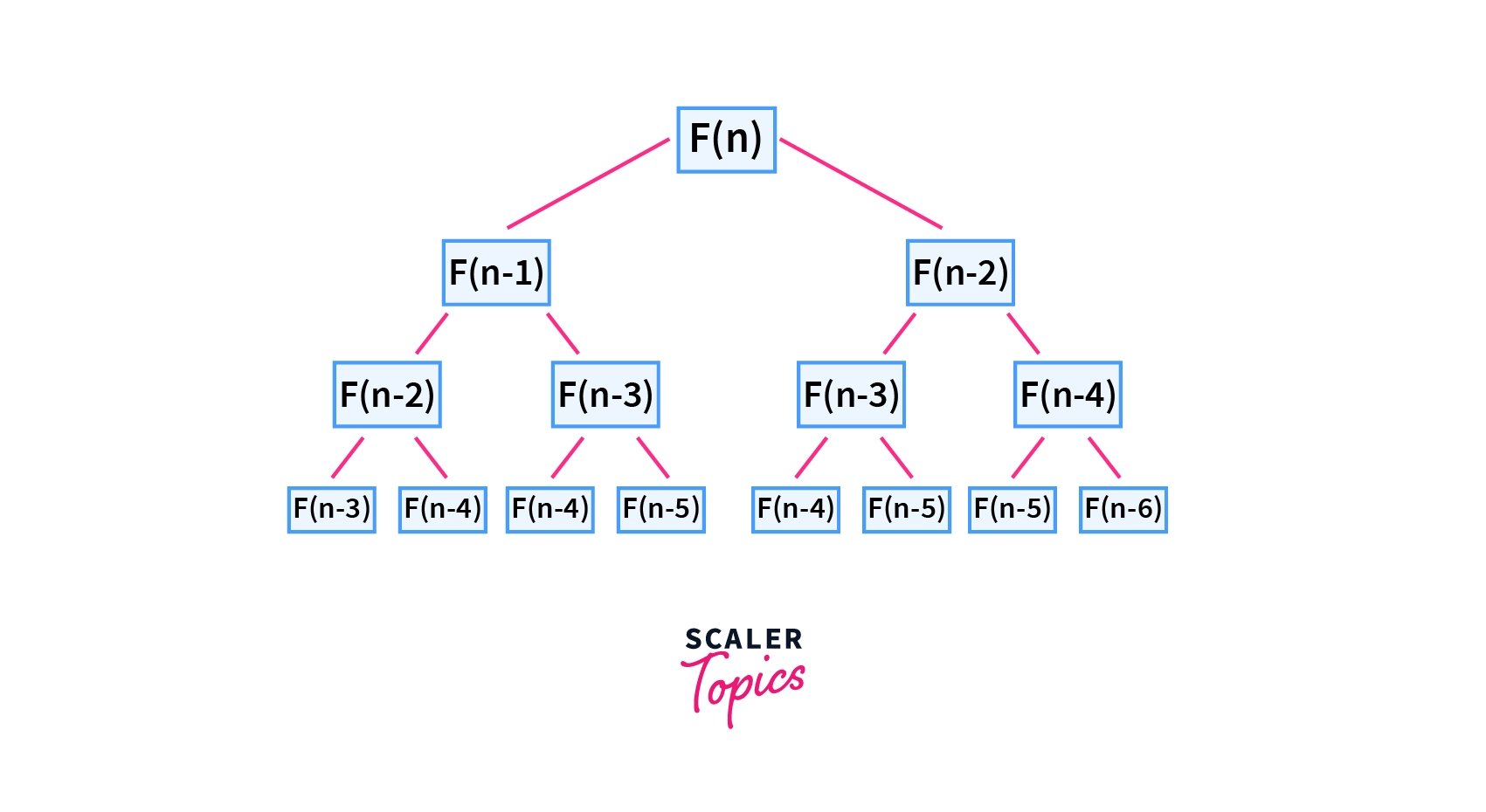
It can be easily observed from the recursion tree that a particular recursive call, say F(n-2) is being used multiple times. In a purely recursive solution, we compute it again and again, hence making the solution unnecessarily expensive in terms of time complexity.
Now if we look at the dynamic Programming approach, instead of recomputing these repeating terms again, we will just store them and use the pre-calculated values, making the solution much more efficient.
Let us look at the dynamic programming solution to find the sixth term of the Fibonacci series.
The process we will follow is:
F[5] = F[3] + F[4]
F[4] = F[2] + F[3]
F[3] = F[1] + F[2]
F[2] = F[0] + F[1]
F[1] = 1 (Base Case)
F[0] = 0 (Base Case)
F[2] = F[0] + F[1] = 0 + 1 = 1
F[3] = F[1] + F[2] = 1 + 1 = 2
F[4] = F[2] + F[3] = 1 + 2 = 3
F[5] = F[3] + F[4] = 2 + 3 = 5If we were not using dynamic programming, we would be calculating two previous terms in each step, but because we have those values already stored, we can just use them, drastically decreasing the time complexity.
Recursion vs. Dynamic Programming
In computer science, recursion is a crucial concept where the solution to a problem depends on solutions to its smaller subproblems.
On the other hand, dynamic programming is an optimization technique for recursive solutions, preferred for solving recursive functions with repeated calls to the same inputs. Recursive functions call themselves during execution, and this process can repeat multiple times unless a base case is present to stop the execution.
However, not all problems using recursion can be solved by dynamic programming unless solutions to the subproblems overlap, requiring a divide-and-conquer method.
For instance, problems like merge, sort, and quicksort are not considered dynamic programming problems as they involve assembling the best answers to non-overlapping subproblems.
How Does It Work?
Dynamic programming tackles complex problems by breaking them into simpler subproblems, solving them optimally, and utilizing memorization to save outcomes for future reference.
1. Top-Down Approach
In the top-down approach, problems are resolved by recursively formulating solutions based on the answers to subproblems. If subproblem answers overlap, they can be memoized or stored in a table for future use.
2. Bottom-Up Approach
The bottom-up method involves writing a solution to a problem in terms of its subproblems, solving smaller subproblems first, and then using their solutions to address larger subproblems.
Characteristics of Dynamic Programming
Two very important characteristics essential for a Dynamic Programming approach to work are:
- Optimal Substructure
- Overlapping Subproblems
Optimal Substructure
If a complex problem has an Optimal Substructure property it means that to find an optimal solution for the problem, the optimal solutions of its smaller subproblems are needed.
So, by combining the optimal solutions of subproblems, we can obtain a solution efficiently.
This property is used by the Dynamic Programming algorithm to ensure a correct solution to the given problem.
Taking the example of the Fibonacci Sequence again, the nth term is given by :
F(n) = F(n-1) + F(n-2)So, to find the nth term, we need to find the correct solution for the (n-1)th and the (n-2)th term, which are smaller subproblems of the complete problem. And again to find the (n-1)th term and the (n-2)th term, we need to find the solution to even smaller subproblems.
Overlapping Subproblems
A problem is said to have an Overlapping Subproblems property if it can be broken down into smaller parts called subproblems, which need to be solved again and again. This means that the same subproblem is needed again and again to generate the final solution.
This property is used by Dynamic Programming in the sense that it stores the solutions to these recurring subproblems so that we do not need to compute it again and again.
For example, in the Fibonacci Sequence problem, we have
F(n) = F(n-1) + F(n-2)
F(n-1) = F(n-2) + F(n-3)
F(n-2) = F(n-3) + F(n-4)
F(n-3) = F(n-4) + F(n-5)From this, it is clear that the subproblems F(n-2), F(n-3), and F(n-4) are used again and again to find the final solution.
Longest Common Subsequence Concept in Dynamic Programming
In dynamic programming, the term “Longest Common Subsequence” (LCS) refers to the shared subsequence among given sequences, and it is the longest one. Unlike the challenge of finding the longest common substring, the components of the LCS don’t need to occupy consecutive locations within the original sequences to be considered part of the problem.
The LCS problem exhibits optimal substructure and overlapping subproblem properties. This implies that the problem can be broken into less complex sub-issues and worked on individually, with solutions to higher-level subproblems often reused in lower-level subproblems, creating overlapping subproblems.
Using dynamic programming for LCS problems is more efficient than a recursive algorithm. Dynamic programming stores the results of each function call, minimizing the need for redundant calculations in future calls.
Dynamic Programming Algorithms
Dynamic programming algorithms solve problems by breaking them into smaller parts until a solution is reached. Here are some primary dynamic programming algorithms:
1. Greedy Algorithms
Greedy algorithms, an example of dynamic programming algorithms, are optimization tools. They solve challenges by searching for optimum solutions to subproblems and combining the findings of these subproblems to get the most optimal answer.
2. Floyd-Warshall Algorithm
The Floyd-Warshall algorithm utilizes dynamic programming to locate the shortest pathways. It determines the shortest route across all pairings of vertices in a graph with weights, supporting both directed and undirected weighted graphs.
Subtypes:
a. Behavior with Negative Cycles
Users can use the Floyd-Warshall algorithm to find negative cycles. This is achieved by inspecting the diagonal path matrix for a negative number, indicating the graph contains a negative cycle.
b. Time Complexity
The Floyd-Warshall algorithm has three loops, each with constant complexity. Consequently, the Floyd-Warshall complexity has a time complexity of O(n^3), where n represents the number of network nodes.
3. Bellman-Ford Algorithm
The Bellman-Ford Algorithm determines the shortest route from a particular source vertex to every other vertex in a weighted digraph. Unlike Dijkstra’s algorithm, it can handle graphs where some edge weights are negative numbers and produces a correct answer.
Note: This algorithm terminates upon finding a negative cycle and can be applied to cycle-canceling techniques in network flow analysis.
Applications of Dynamic Programming
Dynamic programming is a powerful technique with diverse applications in various fields. Here are some common applications:
- Optimization Problems: Solving problems to find the best solution from a set of possibilities.
- Shortest Path Problems: Algorithms like Dijkstra’s and Floyd-Warshall for finding the shortest path in graphs.
- Sequence Alignment: Used in bioinformatics to align biological sequences (DNA, RNA, proteins).
- Text Justification: Arranging text into lines to minimize total extra space.
- String Matching: Efficient string matching using algorithms like Knuth-Morris-Pratt.
- Game Theory: Finding optimal strategies in competitive scenarios.
- Finance and Investment: Portfolio optimization, risk management, and option pricing.
- Robotics and Motion Planning: Motion planning for efficient pathfinding in robotics.
These applications showcase the versatility of dynamic programming in solving complex problems across different domains.
Examples of Dynamic Programming
Here are a few examples of how one may use dynamic programming:
Identifying the number of ways to cover a distance:
- Some recursive functions are invoked three times in the recursion technique, indicating the overlapping subproblem characteristic required to calculate issues that use the dynamic programming methodology.
- Using the top-down technique, just store the value in a HashMap while retaining the recursive structure, then return the value store without calculating each time the function is invoked.
Identifying the optimal strategy of a game:
- To identify the optimal game or gamified experience strategy, let’s consider the “coins in a line” game. The memoization technique is used to compute the maximum value of coins taken by player A for coins numbered h to k, assuming player B plays optimally (Mh,k).
- To find out each player’s strategy, assign values to the coin they pick and the value of the opponent’s coin. After computation, the optimal design for the game is determined by observing the Mh,k value for both players if player A chooses coin h or k.
Counting the number of possible outcomes of a particular die roll:
- With an integer M, the aim is to determine the number of approaches to obtain the sum M by tossing dice repeatedly. The partial recursion tree, where M=8, provides overlapping subproblems when using the recursion method.
- By using dynamic programming, one can optimize the recursive method. One can use an array to store values after computation for reuse.
Conclusion
- Dynamic Programming (DP) is a potent problem-solving paradigm, that breaks down intricate problems into manageable subproblems.
- It optimizes recursive functions by storing and reusing solutions, enhancing efficiency.
- DP operates through top-down and bottom-up approaches, each with unique advantages.
- The LCS problem in DP efficiently identifies the longest shared subsequence, demonstrating its effectiveness.
- Key algorithms, such as Greedy Algorithms, Floyd-Warshall, and Bellman-Ford, highlight DP’s versatility.
- Applications span optimization, shortest paths, bioinformatics, finance, etc.
- DP’s real-world examples showcase its practicality, from game strategies to die roll outcomes.
- In conclusion, DP is a robust, versatile technique, that transforms recursive solutions into efficient algorithms across diverse domains.
Related Topics
Unlock the power of Dynamic Programming and take your coding skills to the next level – Enroll in our Dynamic Programming Course now!