Distance Vector Routing Algorithm

Distance vector is the “Dynamic Routing” protocol. Distant vector protocol also called as Bellman-Ford algorithm used to calculate the shortest path.

What is Distance Vector Routing (DVR) Protocol?

Distant vector routing protocol also called as Bellman-Ford algorithm or Ford Fulkerson algorithm used to calculate a path. A distance-vector protocol calculates the distance and direction of the vector of the next hop from the information obtained by the neighboring router. It is necessary to keep track of the topology and inform neighboring devices if any changes occur in the topology.

Let’s understand a few key points about the distance vector routing protocol:

• Network Information:
  Every node in the network should have information about its neighboring node. Each node in the network is designed to share information with all the nodes in the network.
• Routing Pattern:
  In DVR the data shared by the nodes are transmitted only to that node that is linked directly to one or more nodes in the network.
• Data sharing:
  The nodes share the information with the neighboring node from time to time as there is a change in network topology.

Explanation of Distance Vector Routing Algorithm

Distance vector routing algorithm is also called as Bellman-Ford algorithm or Ford Fulkerson algorithm as this algorithm is used to find the shortest route from one node to another node in the network.

The routing protocol is used to calculate the best route from source to destination based on the distance or hops as its primary metric to define an optimal path. The distance vector refers to the distance to the neighbor nodes, where routing defines the routes to the established node.

The Distance Vector routing algorithm(DVR) shares the information of the routing table with the other routers in the network and keeps the information up-to-date to select an optimal path from source to destination.

The Bellman-Ford algorithm is defined as:

where,
$dx(y)=$ The least distance from x to y

$c(x,v)=$ Node x‘s cost from each of its neighbor v

$dv(y)=$ Distance to each node from initial node

$minv =$ selecting shortest distance

Consider a scenario where all the routers are set and run the distant vector routing algorithm. Each router in the network will share the distance information with the neighboring router. All the information is gathered from the neighbor routers. With each router’s information, an optimal distance is calculated and stored in the routing table. This way, the process of calculating the optimal path is done using the distant vector routing protocol.

How Does DVR Protocol Work?

The distance vector routing algorithm works by having each router maintain a routing table, giving the best-known distance from source to destination and which route is used to get there.

These tables are updated by exchanging the information with the neighbor having a direct link. Tables contain one entry for each route, this entry contains two parts, the preferred outgoing line used to reach the destination or an estimate of the time or distance to that destination.

The metric used can be the number of hops required to reach from source to destination. Time delay in milliseconds, the router can measure it with a special echo signal which the receiver can timestamp and send as soon as possible.

The router exchanges the network topology information periodically with its neighboring node and updates the information in the routing table. The cost of reaching the destination is estimated based on the metric, and an optimal path is obtained to send data packets from source to destination.

Example of Distance Vector Routing

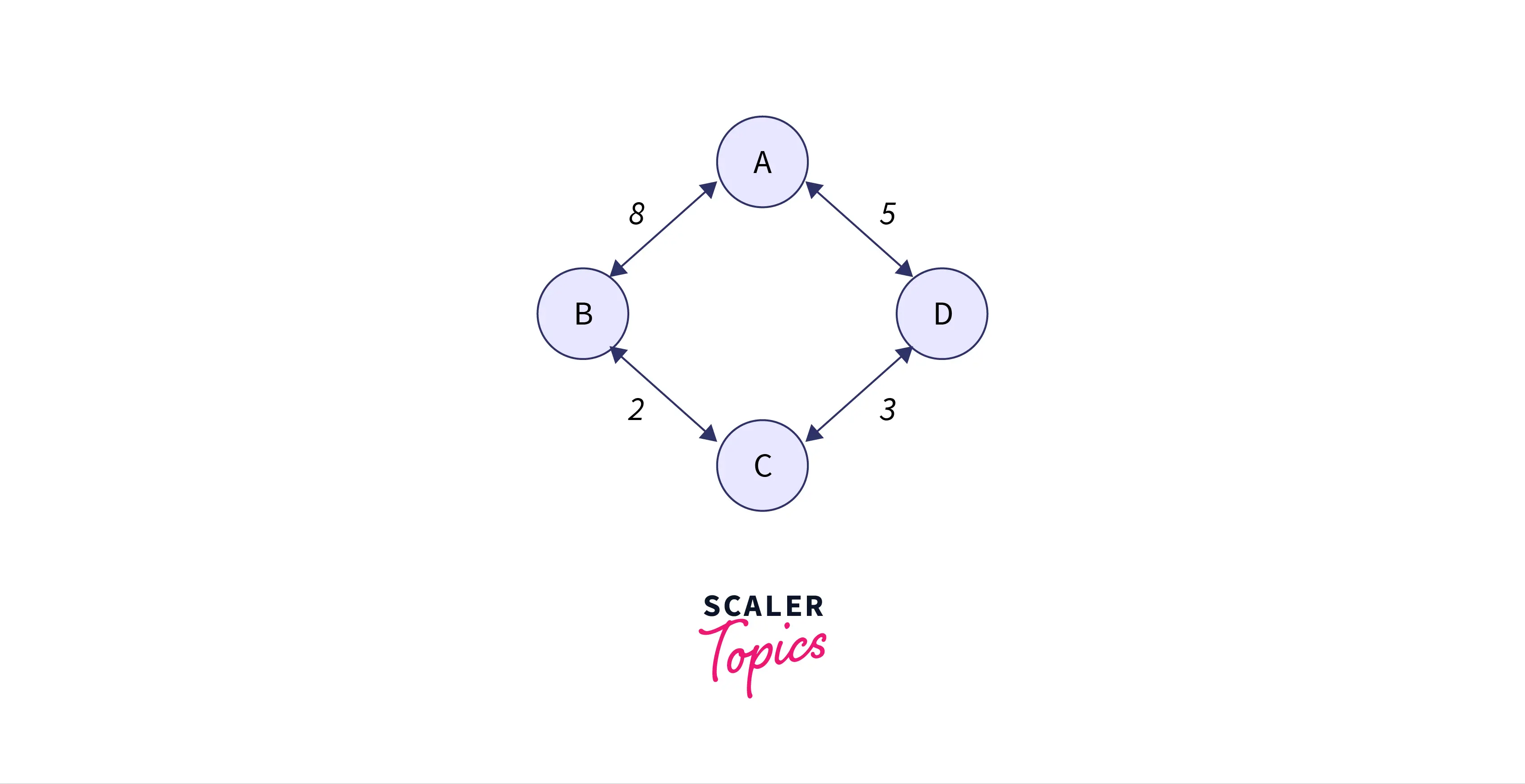
Step – 1

As we can see in the above diagram of the DVR network, the routers in the network start sharing their information with the neighboring routers in the network.

Routing table of A:

Destination	distant	Hop
A	0	A
B	8	B
C	infinity	–
D	5	D

Routing table of B:

Destination	distant	Hop
A	8	A
B	0	B
C	2	C
D	infinity	D

Routing table of C:

Destination	distant	Hop
A	infinity	–
B	2	B
C	0	C
D	3	D

Routing table of D :

Destination	distant	Hop
A	5	A
B	infinity	B
C	3	C
D	0	D

Step – 2

After creating the separate local table this information is shared with the neighboring node having a direct link.

For Router A:

The router A has a direct connection to neighboring routers B and D.

Destination	Vector B	Vector D
A	8	5
B	0	infinity
C	2	3
D	infinity	0

So based on the vector information of the neighboring router, the value of the router is updated.

Here the optimal distance is been calculated to reach the specific destination. First, the distance from A to B is identified, in our case which is 8, ie $cost(A->B)=8$, and $cost(A->D)=5$

The distance to reach a destination B from router A is:

A= min{(A->B+B->A),(A->D+D->B}= min{8+0,5+infinity} = min{8,infinity}= 8(B)

Since the cost is min from neighbor B so the router chooses the path from B. It then updates the routing information with entries $(8, B)$.

To find a cost to reach destination C from router A we will use a similar approach.

A=min{(A->B+B->C),(A->D+D->C}= min{8+2,5+13} =min{10,8} = 8(C)

Distance to reach destination D from A

A=min{(A->B+B->D),(A->D+D->D}= min{8+infinity,5+0} = min{infinity,5} = 5(D)

Consequently, A’s new routing table is:

Destination	distant	Hop
A	0	A
B	8	B
C	8	D
D	5	D

For router B:

Router B receives information from A and C.

The new routing table for B is calculated as:

Destination	Vector A	Vector C
A	0	infinity
B	8	2
C	infinity	0
D	5	3

The cost for vector (B->A)=8
The cost for vector (B->C)=2

Distance to reach destination A from router B:

B=min{(B->A+A->A),(B->C+C->A)}=
min { 8+0 , 2+infinity } = min{8, infinity} = 8(A)

Distance to reach destination C from router B:

B=min{(B->A+A->C),(B->C+C->C)}=
min { 8+infinity , 2+0} = min{infinity, 2} = 2(C)

Distance to reach destination D from router B:

B=min{(B->A+A->D),(B->C+C->D)}=
min { 8+5 , 2+3 } = min{13 , 5 } = 5(C)

Consequently, B’s new routing table is:

Destination	distant	Hop
A	8	A
B	0	B
C	2	C
D	5	C

For router C:

The router C receives information from B and D.

The new routing table for C is calculated as:

Destination	Vector B	Vector D
A	8	5
B	0	infinity
C	2	3
D	infinity	0

The cost(C->B) = 2
The cost(C->D) = 3

Distance to reach destination A from router C:

B=min{(C->B+B->A),(C->D+D->A),}=
min { 2+8 , 3+5  } = min{10,8} = 8(D)

Distance to reach destination B from router C:

B=min{(C->B+B->B),(C->D+D->B),}=
min { 2+0 , 3+infinity  } = 2(B)

Distance to reach destination B from router C:

B=min{(C->B+B->D),(C->D+D->D),}=
min { 2+infinity , 3+0 } = 3(D)

Consequently, C’s new routing table is:

Destination	distant	Hop
A	8	D
B	2	B
C	0	C
D	3	D

For router D:

The router D receives information from A and C.

The new routing table for D is calculated as:

Destination	Vector A	Vector C
A	0	infinity
B	8	2
C	infinity	0
D	5	3

The cost(D->A) = 5
The cost(D->C) = 3

Distance to reach destination A from router D:

D=min{(D->A+A->A),(D->C+C->A)}= min { 5+0 , 3+infinity } = min{5 + infinity} = 5(A)

Distance to reach destination B from router D:

D=min{(D->A+A->B),(D->C+C->B)}=
min { 5+8 , 3+2, } = min{13,5} = 5(C)

Distance to reach destination C from router D:

D=min{(D->A+A->B),(D->C+C->B)}=
min { 5+infinity , 3+0 } = 3(C)

Consequently, D’s new routing table is:

Destination	distant	Hop
A	5	A
B	5	C
C	3	C
D	0	D

Step – 3

After this, the router again exchanges the distance vector obtained in step 2 with its neighboring router.

After exchanging the distance vector, the router prepares a new routing table.

For router A:

Destination	Vector B	Vector D
A	8	5
B	0	5
C	2	3
D	5	0

The cost(A->B) = 8
The cost(A->D) = 5

Distance to reach destination B from router A:

B=min{(A->B+B->B),(A->D+D->B)}=
min { 8+0 , 5+5  } = min{8,10} = 8(B)

Distance to reach destination C from router A:

B=min{(A->B+B->C),(A->D+D->C),}=
min { 8+2 , 5+3 } = min{10,8} = 8(D)

Distance to reach destination D from router A:

B=min{(A->B+B->D),(A->D+D->D),}=
min { 8+5 , 5+0} = min{13,5} = 5(D)

Consequently, A’s new routing table is:

Destination	distant	Hop
A	0	A
B	8	B
C	8	D
D	5	D

For router B:

The router B receives information from A and C.

The new routing table for B is calculated as:

Destination	Vector A	Vector C
A	0	8
B	8	2
C	8	0
D	5	3

The cost for vector (B->A)=8
The cost for vector (B->C)=2

Distance to reach destination A From router B:

B=min{(B->A+A->A),(B->C+C->A)}=
min { 8+0 , 2+8  } = min{8, 10} = 8(A)

Distance to reach destination C From router B:

B=min{(B->A+A->C),(B->C+C->C)}=
min { 8+8 , 2+0 } = 2(C)

Distance to reach destination D From router B:

B=min{(B->A+A->D),(B->C+C->D)}=
min { 8+5 , 2+3 } = min{ 13, 5} = 5(C)

Consequently, B’s new routing table is:

Destination	distant	Hop
A	8	A
B	0	B
C	2	C
D	5	C

For router C:

The router C receives information from B and D.

The new routing table for C is calculated as:

Destination	Vector B	Vector D
A	8	5
B	0	5
C	2	3
D	5	0

The cost(C->B) = 2
The cost(C->D) = 3

Distance to reach destination A from router C:

B=min{(C->B+B->A),(C->D+D->A),}=
min { 2+8 , 3+5  } = min{10,8} = 8(D)

Distance to reach destination B from router C:

B=min{(C->B+B->B),(C->D+D->B),}=
min { 2+0 , 3+5  } = min{2,7} = 2(B)

Distance to reach destination D from router C:

B=min{(C->B+B->D),(C->D+D->D),}=
min { 2+5 , 3+0 } = min(7,3) = 3(D)

Consequently, C’s new routing table is:

Destination	distant	Hop
A	8	D
B	2	B
C	0	C
D	3	D

For router D:

The router D receives information from A and C.

The new routing table for D is calculated as:

Destination	Vector A	Vector C
A	0	8
B	8	2
C	8	0
D	5	3

The cost(D->A) = 5
The cost(D->C) = 3

Distance to reach destination A from router D:

D=min{(D->A+A->A),(D->C+C->A)}=
min { 5+0 , 8+3 } = min{5,11} = 5(A)

Distance to reach destination B from router D:

D=min{(D->A+A->B),(D->C+C->B)}=
min { 5+8 ,  3+2  } = min{13,5} = 5(D)

Distance to reach destination C from router D:

D=min{(D->A+A->B),(D->C+C->B)}=
min { 5+8 , 3+0  } = min{13,3} = 3(C)

Consequently, D’s new routing table is:

Destination	distant	Hop
A	1	A
B	3	C
C	6	C
D	0	D

As you can see in the above network all the link has been used. In the routing table of A link AD and AB is used. In the routing table of B only link BA and BC. In the routing table of C, only llinksCB and CD are used and in D‘s routing table only llinksDA and DC are used.

In this sense, we can also check which of the links can be used and which cannot. In this way, we find the shortest path using the distance vector routing algorithm.
Note:

• In the distance vector routing protocol, only distance vector information is exchanged next-hop values are not exchanged.
• while creating a new routing table, only the distance vector information sis hared that to its neighbor which has a direct link. The old router tables are not taken into consideration only newly updated router information is used.
• The process of updating the routing table keeps on repeating periodically to update the shortest path in case the link goes down or there is a topology change.
• Distance vector routing faces an account-to-infinity problem.

Advantage of Distance Vector Routing

• The distance vector routing protocol is easy to implement for small networks.
• Protocol faces a lower redundancy in the small network.

Disadvantages of Distance Vector Routing

• The distance vector routing faces a slow coverage problem, as it requires more time to get accurate information for the routing table.
• Traffic is created due to periodic changes in the network topology.
• The distance vector routing faces an account-to-infinity problem.

Looking to excel in the world of networks? Our Free Computer Networking course is tailored for beginners & will guide you towards becoming confident in networking.

Conclusion

• Distance vector routing is a type of dynamic protocol.
• Distant vector routing algorithm also called as Bellman-Ford algorithm or Ford Fulkerson algorithm used to calculate the shortest path in the network.
• The router shares the information between the neighboring node containing a direct link.
• The router is used to find the optimal path from source to destination.
• Each router in the network shares a change in topology periodically with the neighboring router