The Disjoint-Set data structure, also known as Union-Find, manages elements in non-overlapping subsets. It’s primarily used for graph connectivity problems, offering two operations: Union, to merge sets, and Find, to identify a set’s leader. This structure excels in tasks involving elements initially represented as separate sets, enabling efficient set combination and connectivity checks between elements. It’s defined by disjoint sets (non-intersecting) and the Union-Find algorithm, which determines subset membership and merges subsets. The Disjoint-Set structure is crucial for problems requiring frequent set merges and connectivity queries, due to its near-constant-time operations.
How to Combine Two Sets?
Whenever we have been given a problem that contains n elements represented as separate sets initially and we need to the perform following operations:
- Combine two sets.
- Find the connectivity of two given elements i.e. whether they belong to the same set or not.
Then it is advisable to use the Disjoint-Set data structure to pose an efficient solution. Disjoint Set Union is sometimes also referred to as Union-Find because of its two important operations –
Disjoint Set: Two sets are called disjoint set if the intersection of two sets is ϕ i.e. NULL. A Disjoint-Set data structure that keeps records of a set of elements partitioned into several non-overlapping (Disjoint) subsets.
Union Find: Union-Find algorithm performs two very useful operations –
Find: To find the subset a particular element ‘k’ belongs to. It is generally used to check if two elements belong to the same subset or not.
Union: It is used to combine two subsets into one. A union query, say Union(x, y) combines the set containing element x and the set containing element y.”
Example of Disjoint Set
In this example, we are going to see how the union queries (series of Union operations) work in a Disjoint Set.
Let’s assume we have 7 nodes initially, we will store them in the form of trees.Where each tree corresponds to one set and the root of the tree will be the parent/leader of the set.

At first, you can see that all the seven nodes are parents of themselves.
In simple words we can say, we have seven different trees containing 1 element each i.e. the root of the tree.
Now we will perform the following union queries one by one on them —
- Union(1, 2)
- Union(2, 3)
- Union(4, 5)
- Union(6, 7)
- Union(5, 6)
- Union(2, 6)
- In our first query Union(
1, 2) we need to join two sets i.e.1and2into one.
After performing the query we can see that,1and2are in the same set with parent/leader as1so our disjoint set will look like –
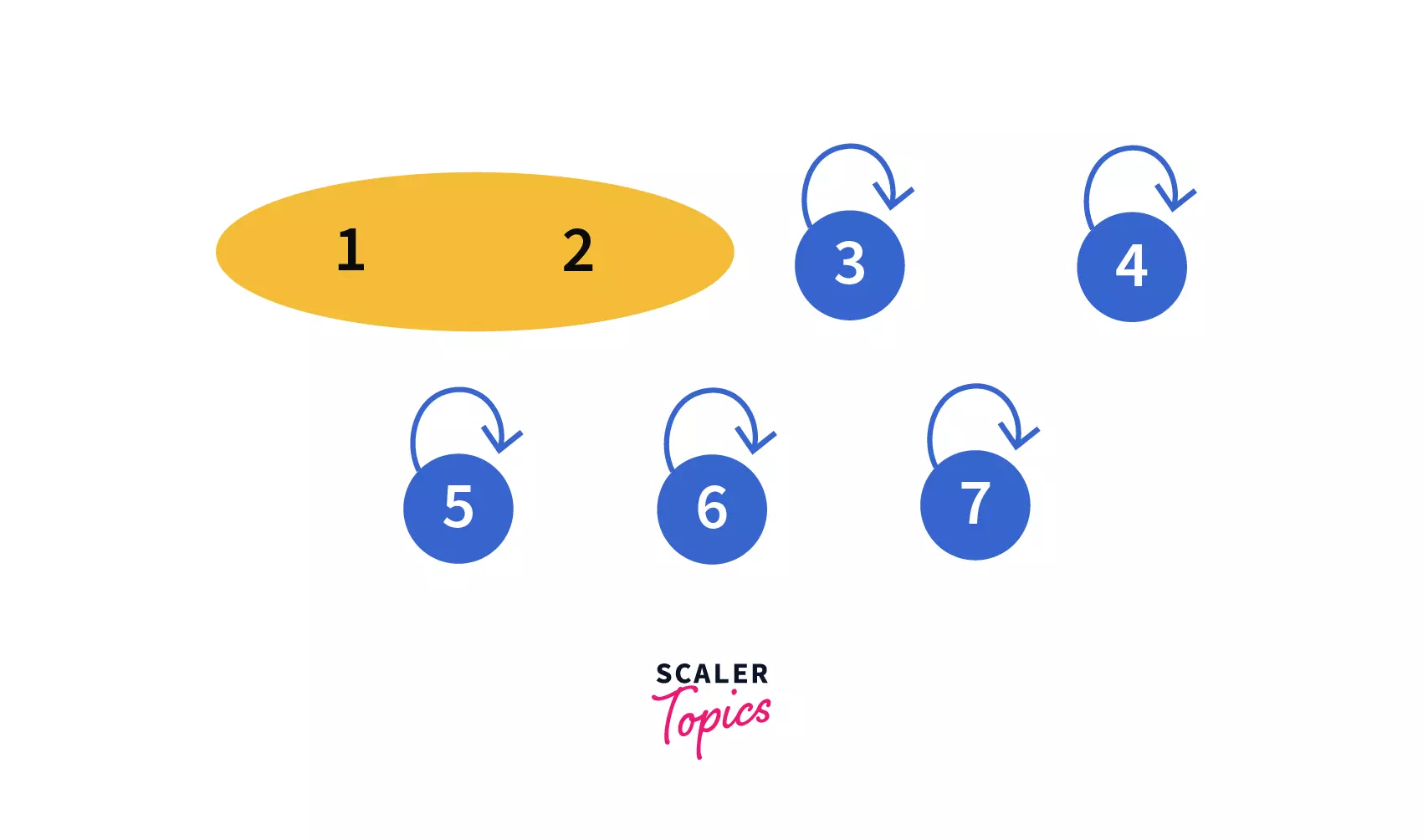
- In our second query, Union(
2, 3) we need to join the sets which contain elements2and3.
After performing the query we can see that,1,2, and3are clubbed into one set so our disjoint set will look like –
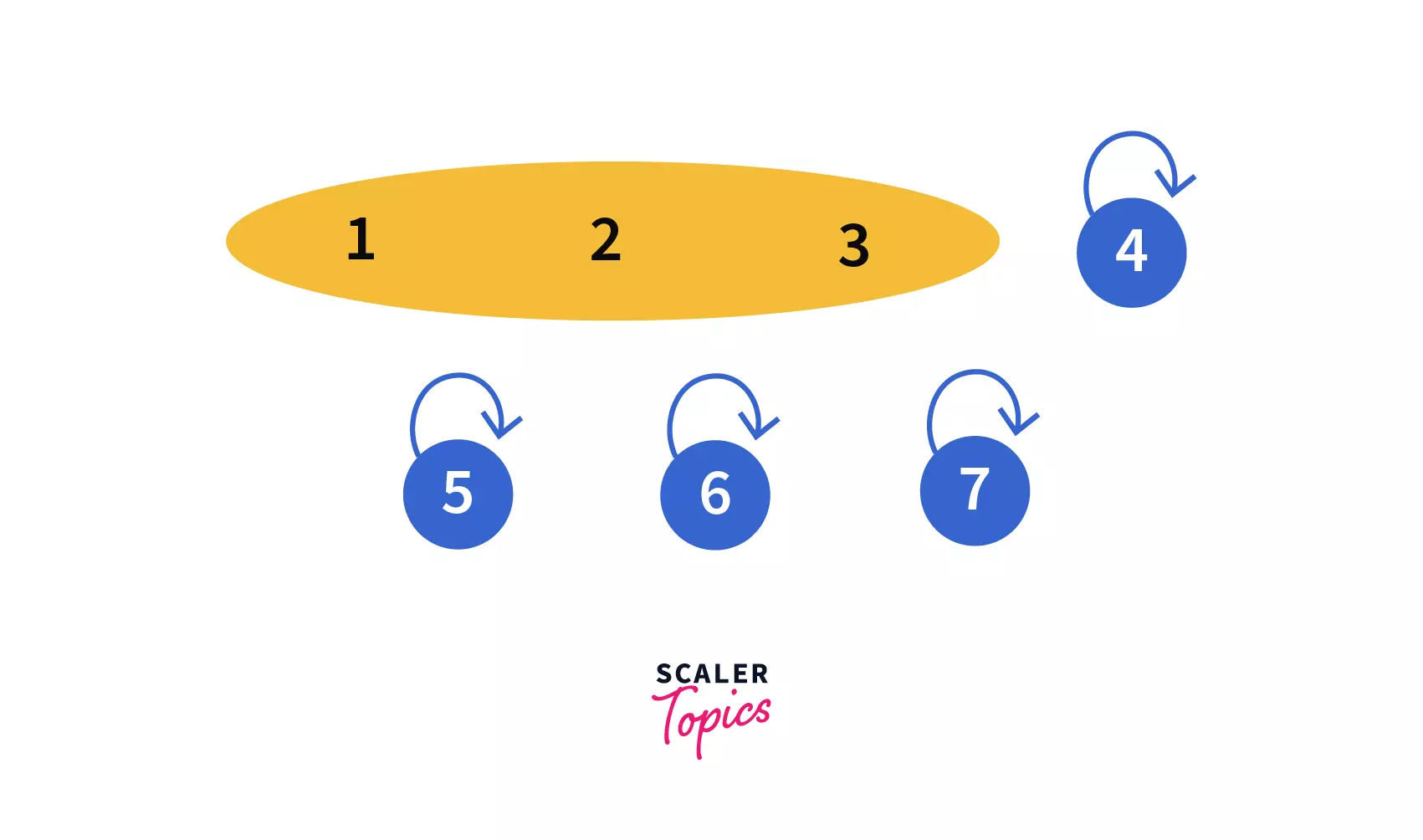
- In our third query, Union(
4, 5) we need to join the sets which contain the elements4and5.
After performing the query we can see that,4and5are in the same set now with parent/leader as4, making our disjoint set like –
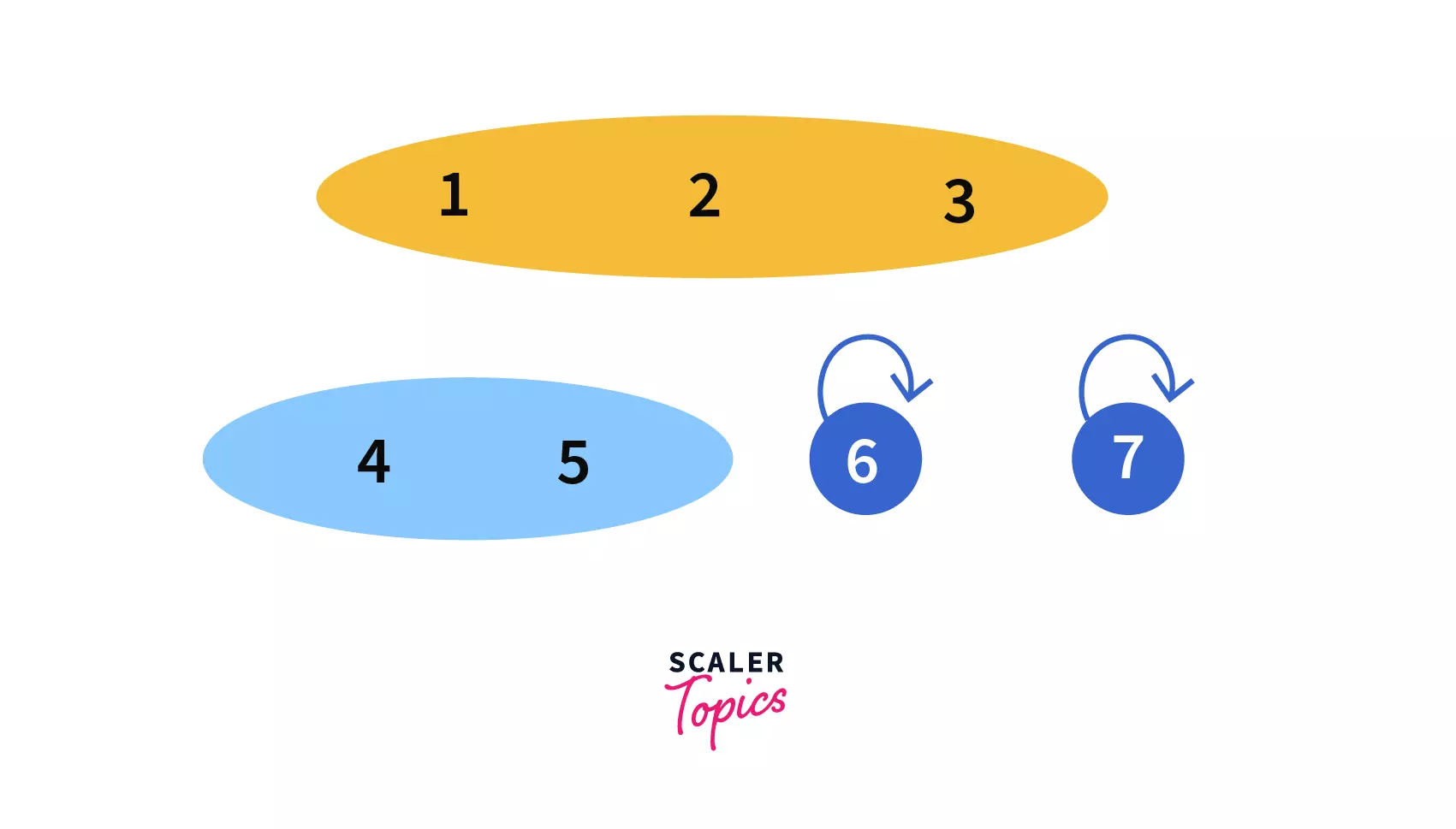
- In our fourth query, Union(
6, 7) we need to join the sets which contain the elements6and7.
After performing the query we can see that,6and7are in the same set now with parent/leader as6, making our disjoint set like –
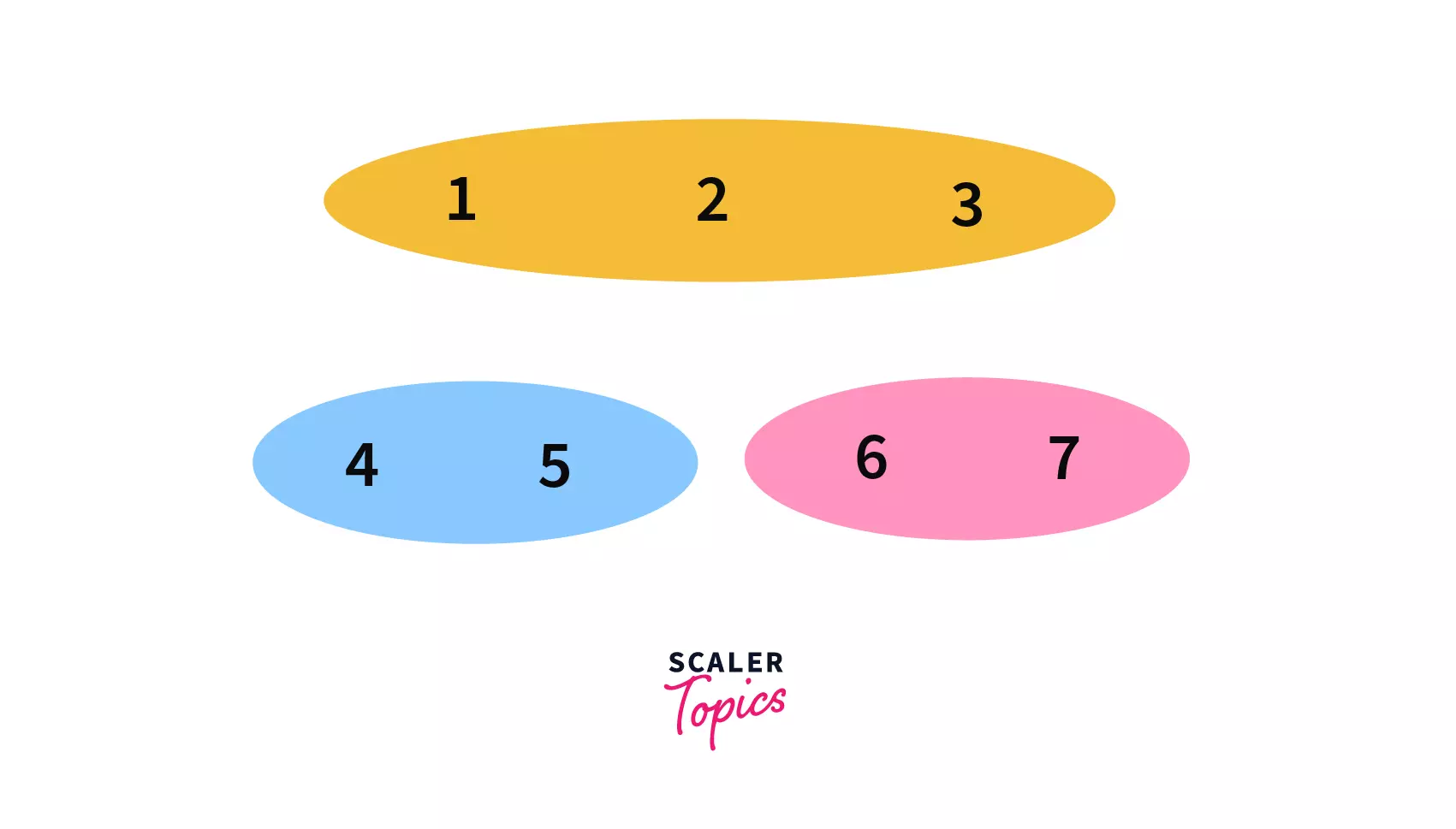
- In our fifth query, Union(
5, 6) we need to join the sets which contain the elements5and6.
After performing the query we can see that,6and7are in the same set now with parent/leader as4, making our disjoint set like –
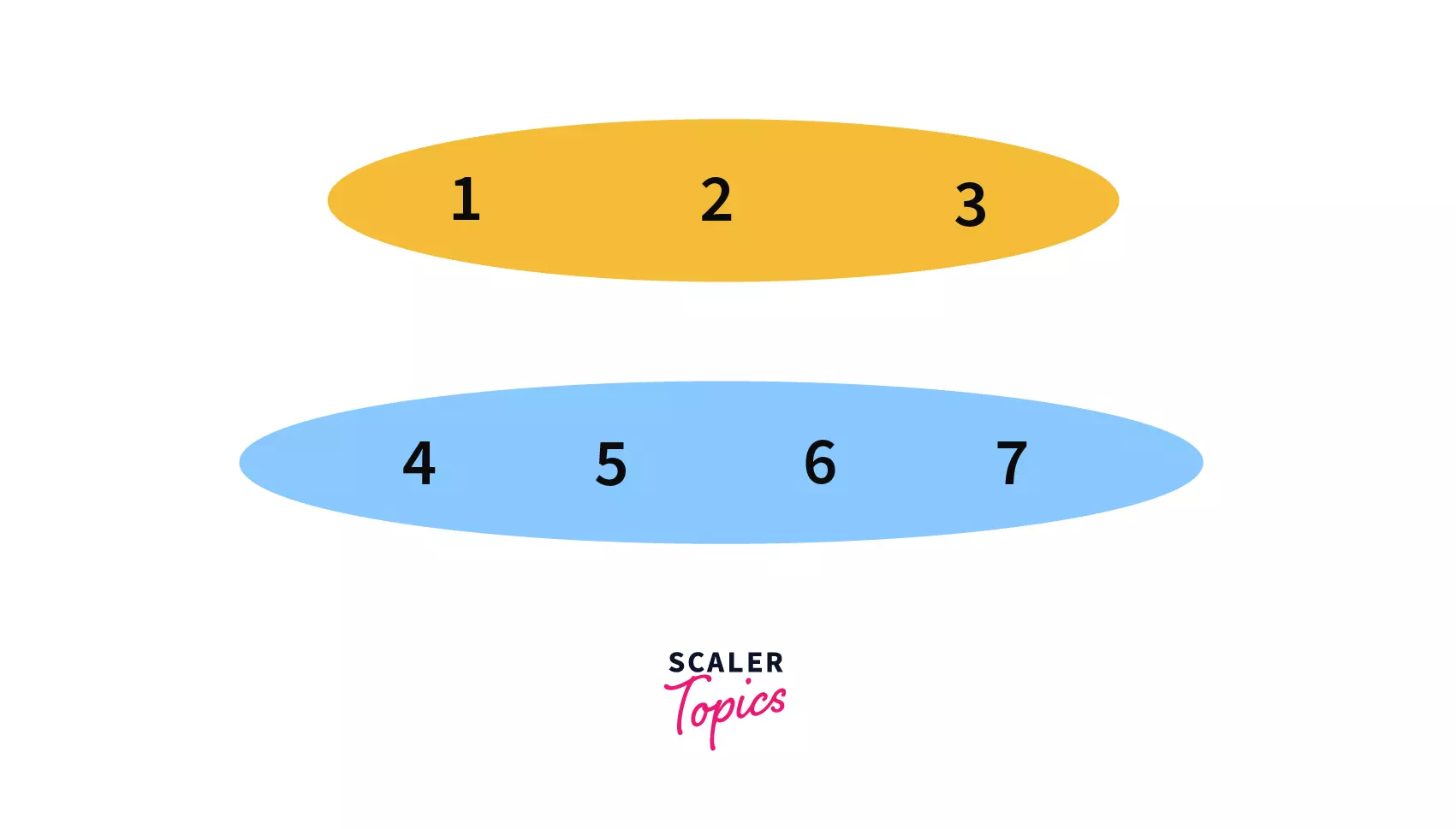
- In our sixth query, Union(
2, 6) we need to join the sets which contain elements2and6.
After performing the query we can see that, all the elements i.e.1to7are in the same set now with parent/leader as1, making our disjoint set like –
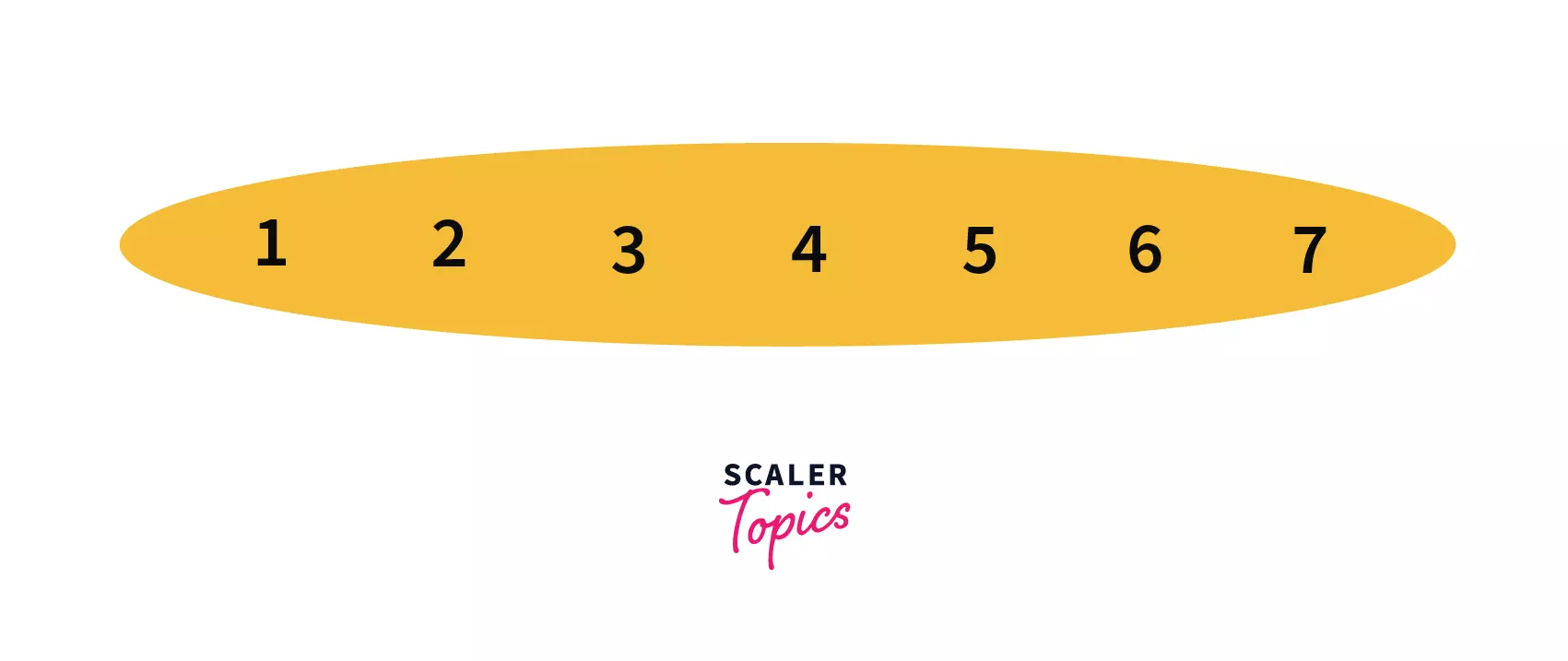
Algorithms
Naive Implementation:
The most basic implementation of the Disjoint set one can think of is to keep a track of the parent of every element present in a list/array.
We will have a global array/list of size n where ‘n’ is the number of elements in the set.
Finding the parent of an element 'u' is very easy, since we are keeping track of parent of every element.
If parent[u]=u then we will return parent[u] in the other case we will recursively find the parent of parent[u] until the condition parent[u]=u satisfies.
For merging two sets, Let we need to perform Union(u, v) then
- We will find parents of
uandv. - If they found different (which means
uandvbelongs to different sets) then we would merge them by makingparent[u]=vorparent[v]=u.
Pseudocode:
parent[n] // A global array of size _n_ such that parent[i]=i
Find(u):
If(parent[u]==u):
Return u
Return Find(parent[u])
Union(u, v):
u = Find(u)
v = Find(v)
If(u!=v):
parent[v] = uAnd that’s it, yes you read it right this is the pseudocode for implementing Disjoint Set data structure, but it is not efficient for large inputs.
Complexity Analysis:
Find– Time complexity of Find operation is $O(n)$ in the worst case (consider the case when all the elements are in the same set and we need to find the parent of a given element then we may need to make n recursive calls).Union– For union query (say Union(u, v)) we need to find the parents of u and v making its time complexity to be $O(n)$.
This approach is not much efficient, so to get the full-fledged advantage of Disjoint Set Union we will look for some minor modifications that can make our code efficient.
Optimization 1 (Path Compression):
Let u be a node and p be its parent. When we are finding parent of u recursively, we are also finding parent of all those intermediate nodes which we visit in the path u → p.
The trick here is to shorten the path to the parent of all those intermediate nodes by directly connecting them to the leader of the set.
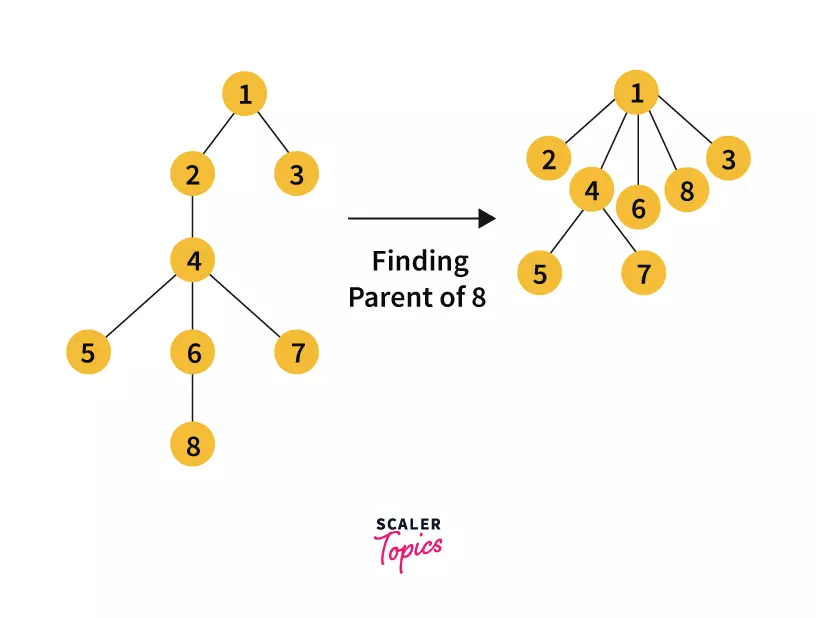
You can see that in the process of finding the parent of node 8 we have attached all the intermediate nodes to 1.
To achieve this, we just need to modify our find function a bit and that minor modification is –
During the recursive call of finding parent of parent[u] we will also pass the result to parent[u] (please refer to the last line of underlying pseudocode for better understanding)
Find(u):
If(parent[u]==u):
Return u
Return parent[u]=Find(parent[u])This is firstly finding the root of the set and in the process of stack unwinding, we are attaching all the intermediate nodes to their representative.
Yes by modifying that line we reduced the time complexity from $O(n)$ to $O(log(n))$
Optimization 2(Union by Rank):
In this optimization, we would be very much careful about which tree is getting attached to the other one.
In the naive implementation, the second tree is always getting attached to the first one which could lead the structure to become like the skewed tree which would have linear chains of length O(n).
So what we will do is, we will maintain a record of the depth of each tree (Rank) and during the union operation we will attach the tree with lower rank to the tree with higher the rank thus Rank of the final tree (after union operation) will remain the same.
In case, if the Rank of both trees is equal we will join any one of them with the other and will increase the rank by 1 of the tree to which another one is joined.
For example –
Suppose we need to perform on give two trees –
Tree 1 –
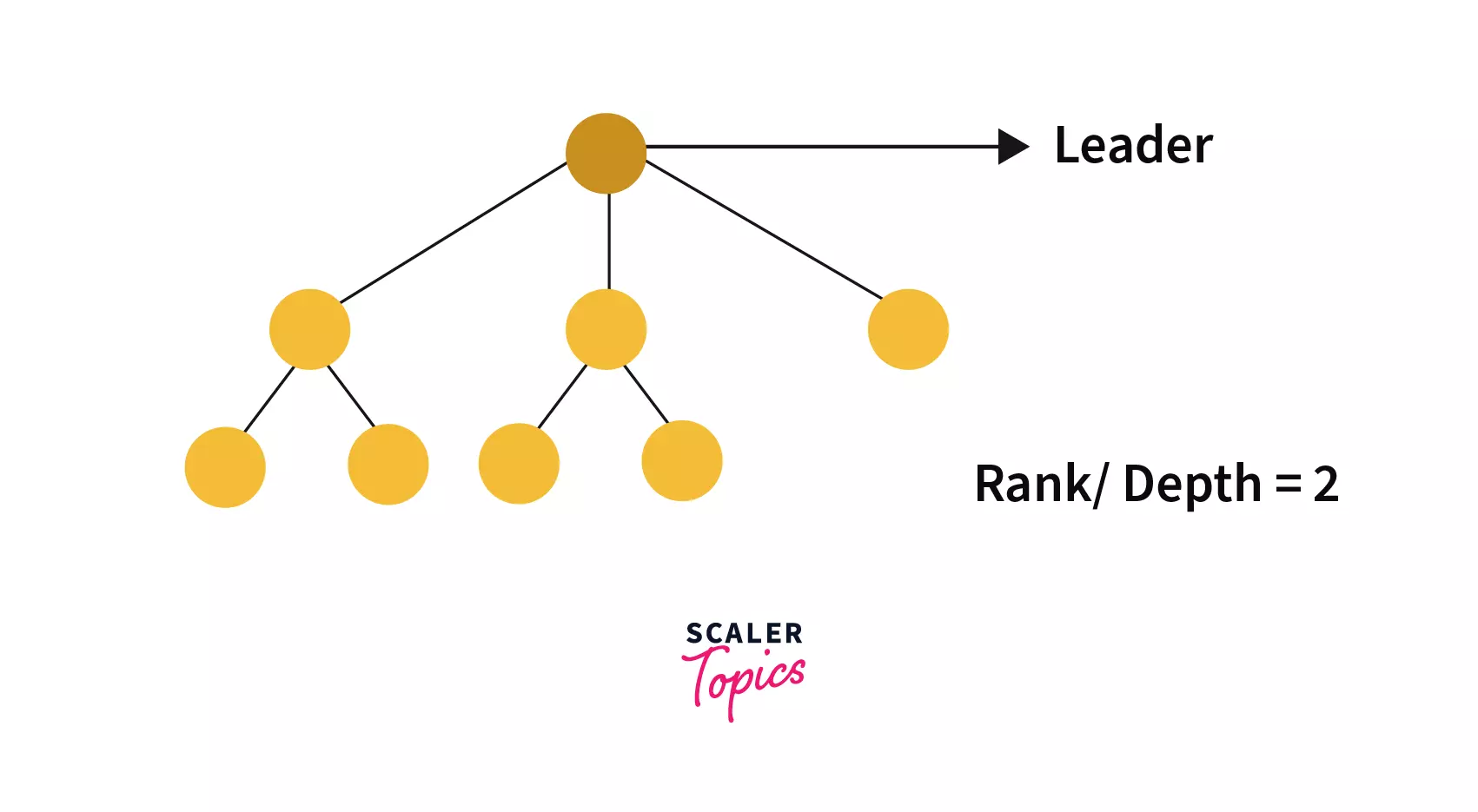
Tree 2 –
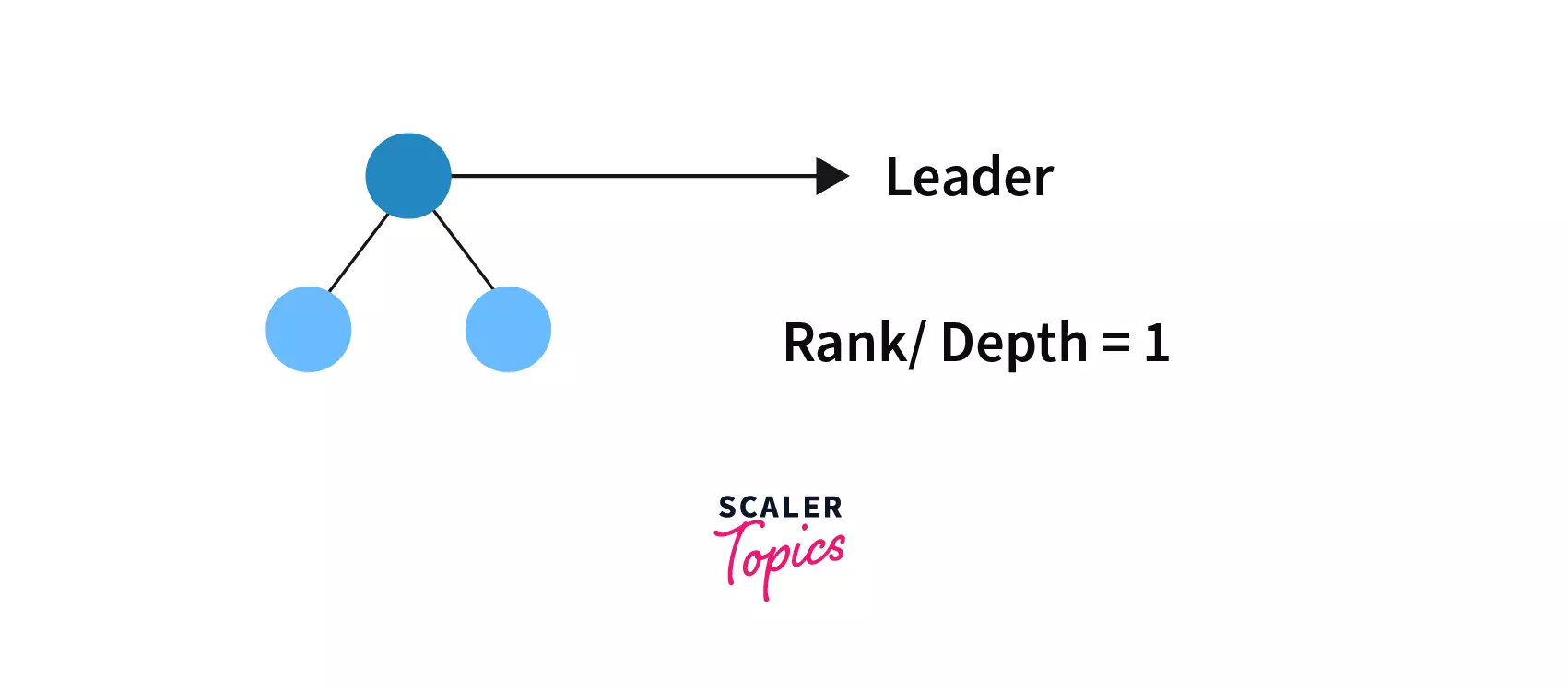
If we combine them by checking their rank then we would find rank [tree1]=2 and rank[tree2]=1 then, the combined tree would be –
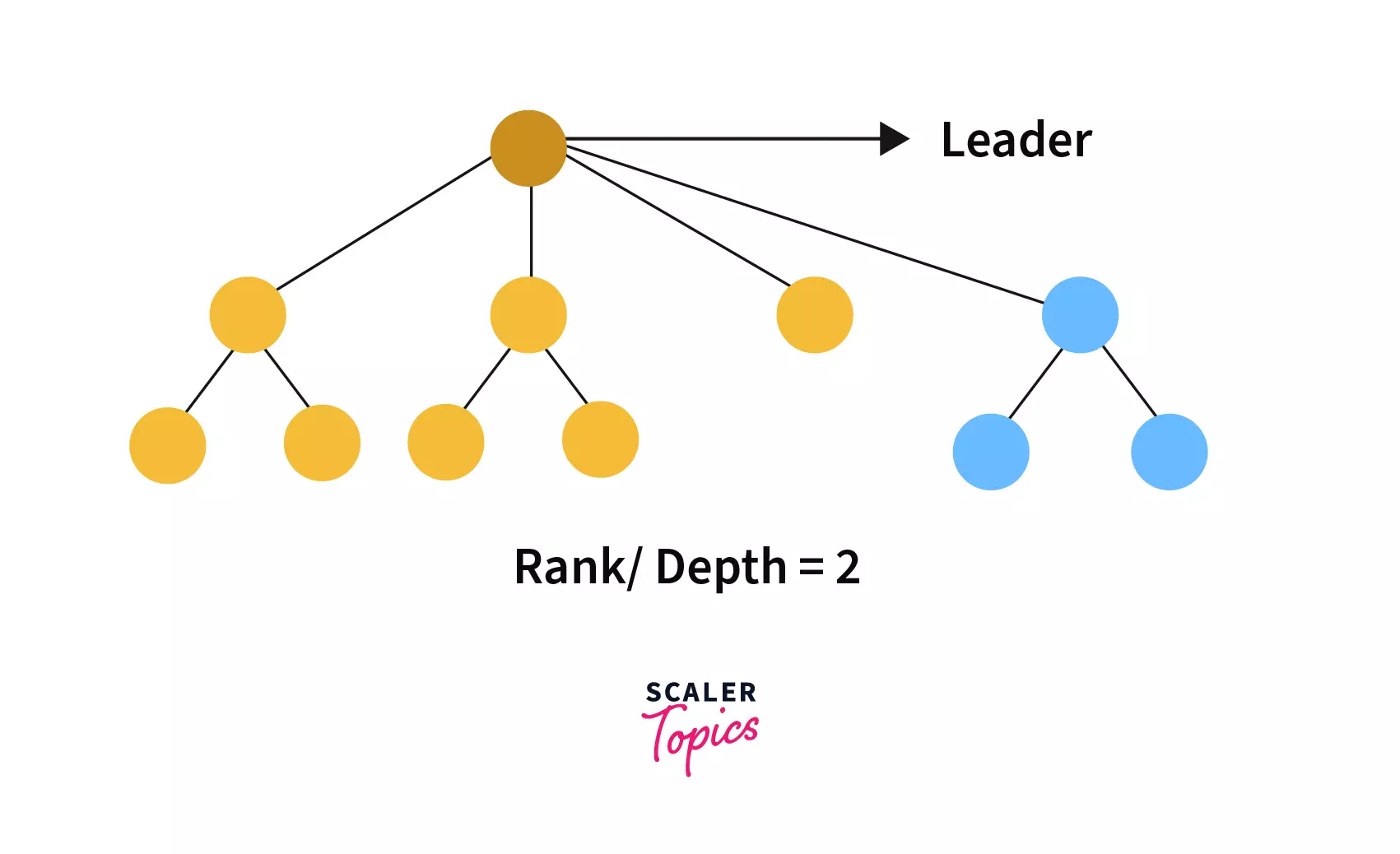
We can see that since tree 2 is attached to tree 1 so, the rank of the combined tree is same as tree 1.
If combine Tree 1 and Tree 2 without checking their rank then the combined tree would look like –
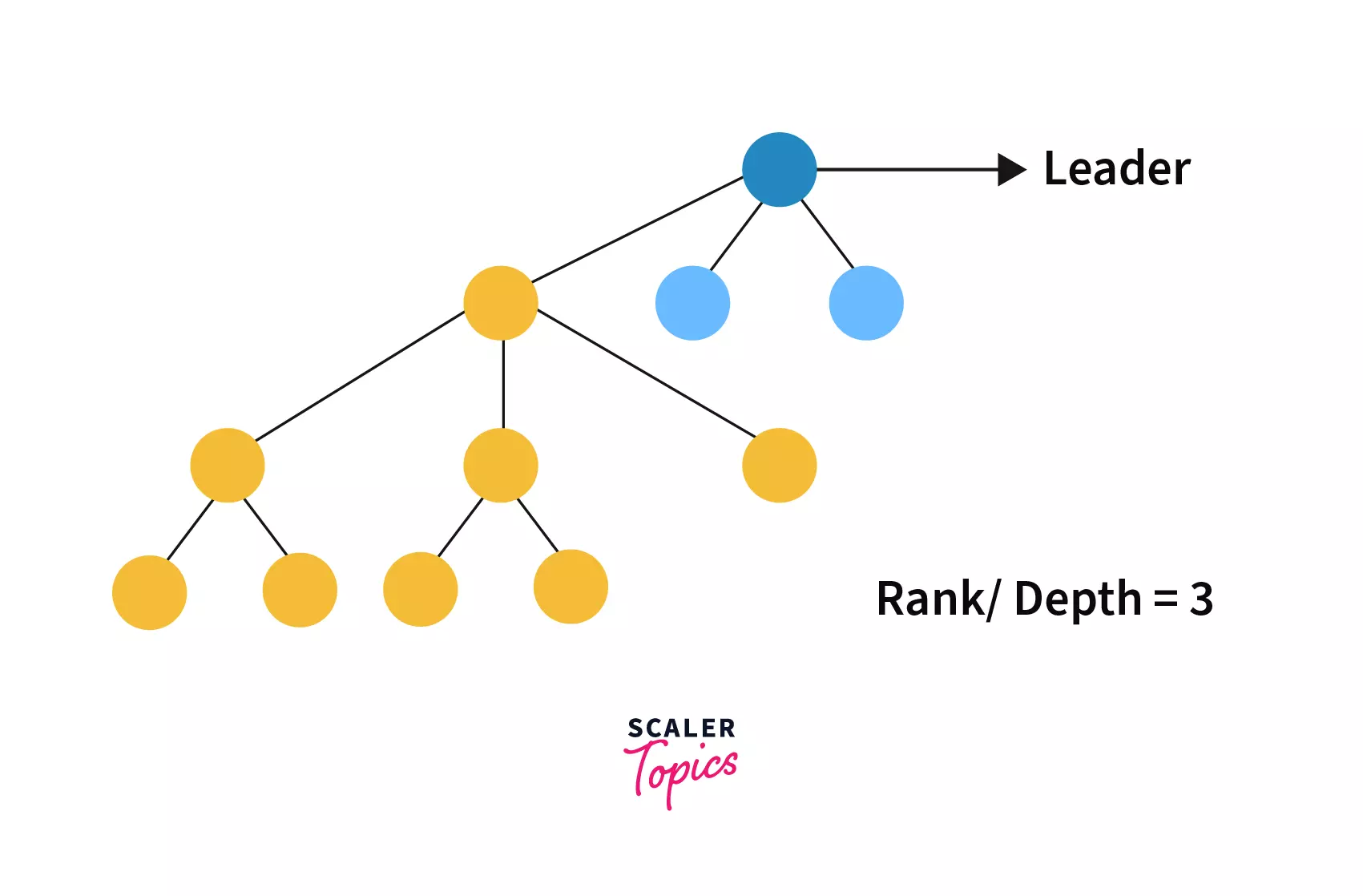
Now we can observe attaching tree 1 to tree 2 is not a good idea as the depth of the combined tree has been increased by 1 which would cost us more time to find the leader of the tree.
The change in algorithm of union function is as follows:
- When merging two sets, we will check which set has a greater rank then we will attach a lower rank tree to the tree with a higher rank.
- In case both trees have equal rank then we will attach anyone of them to other but now we need to increase the rank of the tree to which other is joined by one.
// A global array of size n such that rank[i]=0.
Rank[n]
Union(u, v):
u = Find(u)
v = Find(v)
If(u!=v):
If(Rank[u]<Rank[v]):
Swap(u, v)
parent[v]=u
If(Rank[u]==Rank[v]):
Rank[u]++By doing this modification alone (i.e. without Path compression) we can reduce the time complexity to $O(log(n))$.
Most Optimized Approach:
In optimization 1, we have seen how can we compress the path by directly attaching all the intermediate nodes to the leader of the set during the process of finding the parent of node u the process is termed as “Path Compression“.
In optimization 2, we have seen that how can we minimize the depth of trees by attaching lower rank trees to trees with higher ranks while merging them. The process is termed as “Union by Rank“
So merging optimization 1 and 2 seems to be a good idea, isn’t it? The most optimal approach is the same only i.e. merging Optimization 1 and 2.
If we implement the Find function using Path Compression and the Union function using Union by rank we can achieve the most optimized algorithm.
For implementing we just need two global arrays i.e. parent and rank of size n each to maintain parent and rank of every node present. For Find function we will use the pseudocode used in Optimization 1 and for Union function we will use pseudocode used in Optimization 2.
PesudoCode:
// A global array of size n such that parent[i]=i
parent[n]
// A global array of size n such that rank[i]=0
rank[n]
Find(u):
If(parent[u]==u):
Return u
Return parent[u]=Find(parent[u])
Union(u, v):
u = Find(u)
v = Find(v)
If(u!=v):
If(Rank[u]<Rank[v]):
Swap(u, v)
parent[v]=u
If(Rank[u]==Rank[v]):
Rank[u]++Code:
To make our code more modular let’s make a class to implement $DSU$ with the following data members and methods –
Data Members
- $parent$ – It is an integer type array of size $n$, where $n$ is the number of nodes present. It holds information about parent of each node. Initially, $\forall i, parent[i]=i$
- $rank$ – It is also an integer type array of size $n$ to hold information about rank of a node. Initially, $\forall i, rank[i]=0$.
Methods –
- $Find$ – It is an integer type function which takes one argument $node$. Its main aim is to find leader of set to which $node$ belongs. It is implemented according to the logic discussed in Path compression section.
- $Union$ – It is a void type function which takes two arguments $i.e.$ $u$ and $v$. It merge the set to which $u$ belongs and the set to which $v$ belongs. It is implemented as per the logic discussed in Union by rank section.
- ##### C/C++:
class DSU{
// Declaring two arrays to hold
// information about parent and
// rank of each node.
int *parent;
int *rank;
public:
// Constructor
DSU(int n){
// Defining size of the arrays.
parent=new int[n];
rank=new int[n];
// Initializing their values
// by is and 0s.
for(int i=0;i<n;i++)
{
parent[i]=i;
rank[i]=0;
}
}
// Find function
int find(int node){
// If the node is the parent of
// itself then it is the leader
// of the tree.
if(node==parent[node]) return node;
//Else, finding parent and also
// compressing the paths.
return parent[node]=find(parent[node]);
}
// Union function
void Union(int u,int v){
// Make u as a leader
// of its tree.
u=find(u);
// Make v as a leader
// of its tree.
v=find(v);
// If u and v are not equal,
// because if they are equal then
// it means they are already in
// same tree and it does not make
// sense to perform union operation.
if(u!=v)
{
// Checking tree with
// smaller depth/height.
if(rank[u]<rank[v])
{
int temp=u;
u=v;
v=temp;
}
// Attaching lower rank tree
// to the higher one.
parent[v]=u;
// If now ranks are equal
// increasing rank of u.
if(rank[u]==rank[v])
rank[u]++;
}
}
};Java:
public class DSU{
// Declaring two arrays to hold
// information about the parent and
// rank of each node.
private int parent[];
private int rank[];
// Constructor
DSU(int n){
// Defining size of the arrays.
parent=new int[n];
rank=new int[n];
// Initializing their values
// by is and 0s.
for(int i=0;i<n;i++)
{
parent[i]=i;
rank[i]=0;
}
}
// Find function
public int find(int node){
// If the node is the parent of
// itself then it is the leader
// of the tree.
if(node==parent[node]) return node;
//Else, finding parent and also
// compressing the paths.
return parent[node]=find(parent[node]);
}
// Union function
public void union(int u,int v){
// Make u as a leader
// of its tree.
u=find(u);
// Make v as a leader
// of its tree.
v=find(v);
// If u and v are not equal,
// because if they are equal then
// it means they are already in
// same tree and it does not make
// sense to perform union operation.
if(u!=v)
{
// Checking tree with
// smaller depth/height.
if(rank[u]<rank[v])
{
int temp=u;
u=v;
v=temp;
}
// Attaching lower rank tree
// to the higher one.
parent[v]=u;
// If now ranks are equal
// increasing rank of u.
if(rank[u]==rank[v])
rank[u]++;
}
}
}Python:
class DSU:
# Constructor
def __init__(self, n):
# Declaring two arrays to hold
# information about parent and
# rank of each node.
# &
# Defining size of the arrays.
# Initializing their values
# by is and 0s.
self.parent = [i for i in range(n)]
self.rank = [0 for i in range(n)]
# for i in range(n):
# self.parent.add(i)
# self.rank.add(0);
# Find function
def find(self, node):
# If the node is the parent of
# itself then it is the leader
# of the tree.
if(node==self.parent[node]):
return node
#Else, finding parent and also
# compressing the paths.
self.parent[node] = self.find(self.parent[node])
return self.parent[node]
# Union function
def union(self,u, v):
# Make u as a leader
# of its tree.
u=self.find(u)
# Make v as a leader
# of its tree.
v=self.find(v)
# If u and v are not equal,
# because if they are equal then
# it means they are already in
# same tree and it does not make
# sense to perform union operation.
if(u!=v):
# Checking tree with
# smaller depth/height.
if(self.rank[u]<self.rank[v]):
temp=u
u=v
v=temp
# Attaching lower rank tree
# to the higher one.
self.parent[v]=u
# If now ranks are equal
# increasing rank of u.
if(self.rank[u]==self.rank[v]):
self.rank[u]=self.rank[u]+1Complexity Analysis of Most Optimized Approach:
If we combine both optimizations i.e. Path compression and Union by rank then we can achieve almost constant time complexity.
The final amortized time complexity is calculated to be O($\alpha$(n)), where $\alpha$(n) is inverse Ackermann function which is defined as –
$$\alpha(n)=min{k:A_k(1), \geq n}$$
Where $A_k(j)$ is the Ackermann funcntion it is an extremely rapid growing function and hence it’s inverse i.e. $\alpha$ is extraordinarily slow-growing function is defined by –
$$A_k(j) = A^{(j+1)}_{k-1}(j) $$
Some sample values of Ackermann function are —
| Function | Value |
|---|---|
| A0(1) | 1 |
| A1(1) | 3 |
| A2(1) | 7 |
| A3(1) | 2047 |
| A4(1) | >>1080 |
The growth of function is too slow and hence the value of $\alpha(n)$ would not exceed 5 for any n $\leq$ 10600 as otherwise, n would be more than the total number of atoms present in the universe.
Applications of Disjoint Set
- It is used to find Cycle in a graph as in Kruskal’s algorithm, DSUs are used.
- Checking for connected components in a graph.
- Searching for connected components in an image.
Boost your C++ proficiency with our expertly designed Data Structures in C++ Certification Course. Get started now!
Conclusion
- In this blog, we have discussed one of the important data structures i.e.
Disjoint Set & Unionwhich is used to find the connectivity of different components in a graph efficiently. - We have seen the naive approach to implement DSU then we have seen several optimizations viz. Path compression and Union by rank. Also, we have seen the most optimized approach with almost constant time complexity.
- It can also be used for several other types of problems where we need to process many queries in which we have to check whether two objects are connected directly or indirectly.