An array is a linear collection of values stored at contiguous memory locations. A subarray is nothing but a slice of these contiguous memory locations of the actual array or we can say that a subarray is nothing but any contiguous part of a given array. A subset is often confused with subarray and subsequence but a subset is nothing but any possible combination of the original array (or a set). Now, a subsequence is a sequence of the elements of the array obtained by deleting some elements of the array. The subsequence should not be confused with the subarray or substring. The subarray or substring is contiguous but a subsequence need not be contiguous.
Difference Between Subarray, Subset and Subsequence
Before learning about the difference between subarray, subset, and subsequence, let us first get a brief introduction to arrays.
An array is a linear collection of values stored at contiguous memory locations. Array stores homogeneous values(similar data type values).
Some of the important points to keep in mind regarding arrays are as follows:
- The arrays occupy continuous (contiguous) space in the memory.
- The indexing of the array starts with 0 and goes on to (length of array – 1).
- Arrays are of fixed length, i.e. after the creation of an array, we cannot change the size of the array.
- The access of elements is very fast in arrays. We can easily access any element using the index of the array.
Example: The array os 56, 50, 34, 24, 12 will look like:
To learn more about arrays, refer to the article – Arrays in Data Structure.
Note: A list is used to store one or more objects or data elements. Lists are used in python and java mostly. We can say that lists are similar to arrays.
Let us now learn about subarray vs subsequence vs subset in detail.
Definition of Subarray and Example
As we know that an array is a linear collection of values stored at contiguous memory locations. So, what is subarray? Well, a subarray is nothing but a slice of these contiguous memory locations of the actual array. In simpler terms, a subarray is nothing but any contiguous part of a given array. The subarray has the same sequence of elements (order of the elements) as it is in the array.
A subarray is also known as a contiguous subarray. Although a subarray is contiguous (continuous) in nature.
Example: Let the array be: arr = [1, 2, 3] Then one subarray of arr can be: subarray = [1, 2] All the sub-arrays of arr are:
- [1]
- [2]
- [3]
- [1, 2]
- [2, 3]
- [1, 2, 3]
So, we conclude that the size of the subarray can range from 1 to the size of the actual array.
Refer to the following section to learn how to generate all the subarrays of a particular array along with the implementation.
Definition of Subset and Example
A subset is often confused with subarray and subsequence but a subset is nothing but any possible combination of the original array (or a set).
For example, the subsets of array arr = [1, 2, 3, 4, 5] can be:
- [3, 1]
- [2, 5]
- [1, 2], etc.
So, we can conclude that subset is the superset of subarrays i.e. all the subarrays are subsets but vice versa is not true.
Refer to the following section to learn how to generate the subsets of a particular array along with the implementation.
Definition of Subsequence and Example
As the name suggests, a subsequence is a sequence of the elements of the array obtained by deleting some elements of the array. One important thing related to the subsequence is that even after deleting some elements, the sequence of the array elements is not changed. Both the string and arrays can have subsequences.
The subsequence should not be confused with the subarray or substring. The subarray or substring is contiguous but a subsequence need not to be contiguous.
For example, the subsequences of the array arr : [1, 2, 3, 4] can be:
- [1, 3]
- [2, 3, 4]
- [1, 2, 3, 4], etc.
Note: A subarray is a subsequence, a subsequence is a subset but the reverse order is not correct.
Refer to the following section to learn how to generate the subsequence of a particular array along with the implementation.
Number of subarrays, subset, subsequence we can form using a array of size n.
Let us learn how many subsets, subsequences, and subarrays can an array (arr) of size n have.
As we know, a subarray is a slice of the contiguous memory locations of the array. So, we can have n * (n+1)/2 non-empty subarrays of an array.
Now, a subset is nothing but any possible combination of the original array (or a set). We can have 2^(size of the array) i.e. 2^n subsets of an array.
A subsequence is a sequence of the elements of the array obtained by deleting some elements of the array and preserving the order of the array elements. We can have2^n subsequences of an array since we keep the original ordering, this is the same as subsets of an array.
For example, if the size of the array is 3 then
- The number of subarrays is 6.
- The number of the subsequences is 8.
- The number of subsets is 8.
Let us learn how to generate all the subsets, subsequences, and subarrays of a particular array using code.
Code to find All Subarrays.
A subarray is a slice of the contiguous memory locations of the array. So, to generate the subarrays of an array, we can use nested loops (two arrays). We will pick one element in the first iteration and then run an inner loop that will consider all the elements on the right of the picked elements as ending elements of the subarray.
Refer to the code for a better understanding.
C++
#include <bits/stdc++.h>
using namespace std;
void generateSubArrays(int arr[], int n) {
// Picking one element in each outer loop
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
/*
Printing the subarray between the current starting point i.e. i and the current ending point i.e. j
*/
for (int k = i; k <= j; k++)
cout << arr[k] << " ";
cout << endl;
}
}
}
int main() {
int arr[] = {1, 2, 3};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "All the subarrays are: " << endl;
generateSubArrays(arr, n);
return 0;
}
Python
def generateSubArrays(arr, n):
# Picking one element in each outer loop
for i in range(0, n):
for j in range(i, n):
"""
Printing the subarray between the current starting point i.e. i and the current ending point i.e. j
"""
for k in range(i, j+1):
print(arr[k], end=" ")
print()
arr = [1, 2, 3]
print("All the subarrays are: ")
generateSubArrays(arr, len(arr))
Java
public class Test {
static void generateSubArrays(int arr[], int n) {
// Picking one element in each outer loop
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
/*
Printing the subarray between the current starting point i.e. i and the current
ending point i.e. j
*/
for (int k = i; k <= j; k++)
System.out.print(arr[k] + " ");
System.out.println();
}
}
}
public static void main(String args[]) {
int arr[] = { 1, 2, 3 };
System.out.println("All the subarrays are: ");
generateSubArrays(arr, arr.length);
}
}Output:
All the subarrays are:
1
1 2
1 2 3
2
2 3
3
Time and Space Complexity
For generating all the subarrays of an array, we are using two loops i.e nested loops and we are not using any extra space.
Time Complexity
The time complexity of generating all the subarrays of an array is O(n^2), where n is the size of the array.
Space Complexity
Since we are not using any extra space, the space complexity of generating all the subarrays of an array is O(1).
Code to Find All Subsets
A subset is nothing but any possible combination of the original array (or a set). So, to generate the subsets of an array, we can use the generate power set algorithm.
We first calculate the power set for the array i.e. the 2 to the power n (size of the array). Then we would run a loop from 0 to the power set and inside the loop, we would run an inner loop that will check some conditions, and based on the conditions the subsets are printed.
Now, in the inner loop, we will check if the ith bit in the counter is set or not. If it is set, print the ith element from the array for this subset.
Refer to the code for a better understanding.
C++
#include <bits/stdc++.h>
using namespace std;
void generateSubsets(int arr[], int n) {
// calculating the power set for the array.
int powerSet = pow(2, n);
// Running a counter loop form 0 to to powerSet.
for (int counter = 0; counter < powerSet; counter++) {
for (int i = 0; i < n; i++) {
// if the i-th bit is set then print the i-th element
if (counter & (1 << i))
cout << arr[i] << " ";
}
cout << endl;
}
}
int main() {
int arr[] = {1, 2, 3};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "All the subsets are: " << endl;
generateSubsets(arr, n);
return 0;
}Python
def generateSubsets(arr, n):
# calculating the power set for the array.
powerSet = pow(2, n)
# Running a counter loop form 0 to to powerSet.
for counter in range(0, powerSet):
for i in range(0, n):
# f the i-th bit is set then print the i-th element
if((counter & (1 << i)) > 0):
print(arr[i], end=" ")
print("")
arr = [1, 2, 3]
print("All the subsets are: ")
generateSubsets(arr, len(arr))Java
public class Test {
static void generateSubsets(int arr[], int n) {
// calculating the power set for the array.
long powerSet = (long) Math.pow(2, n);
// Running a counter loop form 0 to to powerSet.
for (int counter = 0; counter < powerSet; counter++) {
for (int i = 0; i < n; i++) {
// if the i-th bit is set then print the i-th element
if ((counter & (1 << i)) > 0)
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
public static void main(String args[]) {
int arr[] = { 1, 2, 3 };
System.out.println("All the subsets are: ");
generateSubsets(arr, arr.length);
}
}
Output:
All the subsets are:
1
2
1 2
3
1 3
2 3
1 2 3Time and Space Complexity
For generating all the subsets of an array, we are using two loops i.e nested loops and we are not using any extra space.
Time Complexity
The time complexity of generating all the subsets of an array is O(2^n), where n is the size of the array.
Space Complexity
Since we are not using any extra space, the space complexity of generating all the subsets of an array is O(1).
Code to Find All Subsequences
A subsequence is a sequence of the elements of the array obtained by deleting some elements of the array. So, to generate the subsequences of an array, we can use the recursion concept.
Note: Recursion is a widely used technique in computer science used to solve complex problems by breaking the problem into simpler ones. Recursion is a process in which a function calls itself directly or indirectly. The corresponding function is called a recursive function.
So, for every element of an array, we have two choices, either include the current element in the subsequence or exclude it. We will apply this logic for every element starting from the first element till the last element of the array.
Let us take a diagram to understand the recursion calls for better understanding.
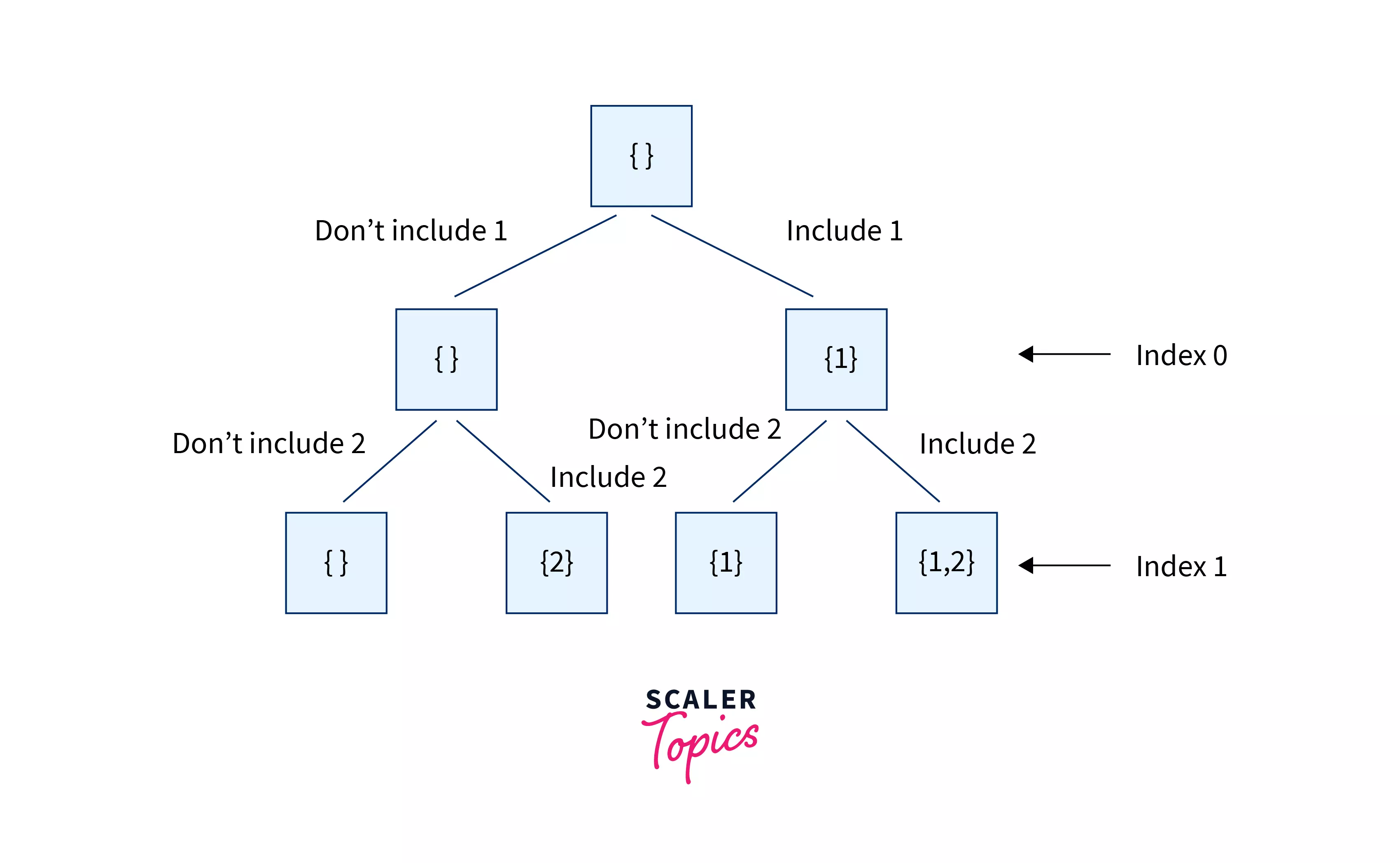
Refer to the code for a better understanding.
C++
#include <bits/stdc++.h>
using namespace std;
void generateSubsequences(int arr[], int index, vector<int> subarray, int n) {
// Print the subsequences when we reach the end of recursion tree.
if (index == n) {
for (auto i : subarray)
cout << i << " ";
if (subarray.size() == 0)
cout << "[]";
cout << endl;
return;
}
else {
// adding the current index into the subsequence and calling the recursive function.
subarray.push_back(arr[index]);
generateSubsequences(arr, index + 1, subarray, n);
// removing the added index into the subsequence.
subarray.pop_back();
// not adding the current element into the subsequence.
generateSubsequences(arr, index + 1, subarray, n);
}
}
int main() {
int arr[] = {1, 2, 3};
int n = sizeof(arr) / sizeof(arr[0]);
vector<int> subarray;
cout << "All the subsequences are: " << endl;
generateSubsequences(arr, 0, subarray, n);
return 0;
}
Python
def generateSubsequences(arr, index, subarray):
# Print the subsequences when we reach the end of the recursion tree.
if index == len(arr):
if len(subarray) != 0:
for i in subarray:
print(i, end=" ")
print()
else:
print("[]")
else:
# not adding the current element into the subsequence.
generateSubsequences(arr, index + 1, subarray)
# adding the current index into the subsequence and calling the recursive function.
generateSubsequences(arr, index + 1,
subarray+[arr[index]])
return
arr = [1, 2, 3]
print("All the subsequences are: ")
generateSubsequences(arr, 0, [])
Java
import java.util.*;
public class Test {
static void generateSubsequences(int[] arr, int index,
ArrayList<Integer> subarray) {
// Print the subsequences when we reach the end of recursion tree.
if (index == arr.length) {
if (subarray.size() > 0) {
for (int i = 0; i < subarray.size(); i++)
System.out.print(subarray.get(i) + " ");
System.out.println();
} else {
System.out.println("[]");
}
} else {
// adding the current index into the subsequence and calling the recursive
// function.
generateSubsequences(arr, index + 1, subarray);
subarray.add(arr[index]);
// not adding the current element into the subsequence.
generateSubsequences(arr, index + 1, subarray);
// removing the added index into the subsequence.
subarray.remove(subarray.size() - 1);
}
return;
}
public static void main(String args[]) {
int arr[] = { 1, 2, 3 };
ArrayList<Integer> subarray = new ArrayList<>();
System.out.println("All the subsets are: ");
generateSubsequences(arr, 0, subarray);
}
}Output:
All the subsequences are:
1 2 3
1 2
1 3
1
2 3
2
3
[]
Time and Space Complexity
For generating all the subsequences of an array, we are recursion and for each array element, we are either adding or not adding it into the subsequence. For this, we are using the recursion stack of the memory.
Time Complexity
The time complexity of generating all the subsequences of an array is O(2^n), where n is the size of the array.
Space Complexity
Since we are using extra space as a recursion stack, the space complexity of generating all the subsets of an array is O(n), where n is the size of the recursion stack.
Conclusion
- An array is a linear collection of values stored at contiguous memory locations. Array stores homogeneous values.
- A subarray is a slice of the contiguous memory locations of the array. We can have n * (n+1)/2 non-empty subarrays of an array.
- A subset is nothing but any possible combination of the original array (or a set). We can have 2^(size of the array) i.e. 2^n subsets of an array.
- A subsequence is a sequence of the elements of the array obtained by deleting some elements of the array and preserving the order of the array elements. We can have 2^n subsequences of an array.
- To generate the subarrays of an array, we can use nested loops. We will pick one element and then run an inner loop which will consider all the elements on the right of the picked elements as ending elements of the subarray.
- The time complexity of generating all the subarrays of an array is O(n^2), where n is the size of the array. The space complexity of generating all the subarrays of an array is O(1).
- To generate the subsets of an array, we can use the generate power set algorithm.
- The time complexity of generating all the subsets of an array is O(2^n), where n is the size of the array. The space complexity of generating all the subsets of an array isO(1).
- To generate the subsequences of an array, we can use the recursion. For every element of an array, we can either include the current element in the subsequence or exclude it. We will apply this logic for every element starting from the first element till the last element of the array.
- The time complexity of generating all the subsequences of an array is O(2^n), where n is the size of the array. The space complexity of generating all the subsets of an array is O(n), where n is the size of the recursion stack.