A Heap is a special tree-based data structure where the tree is organized as a complete binary tree. Due to this structure, a heap with N nodes has a height of log N. It’s particularly valuable for efficiently removing the highest or lowest priority element. Typically represented as an array, there are two main types of heaps in data structures: Min-Heap and Max-Heap.
Min Heap
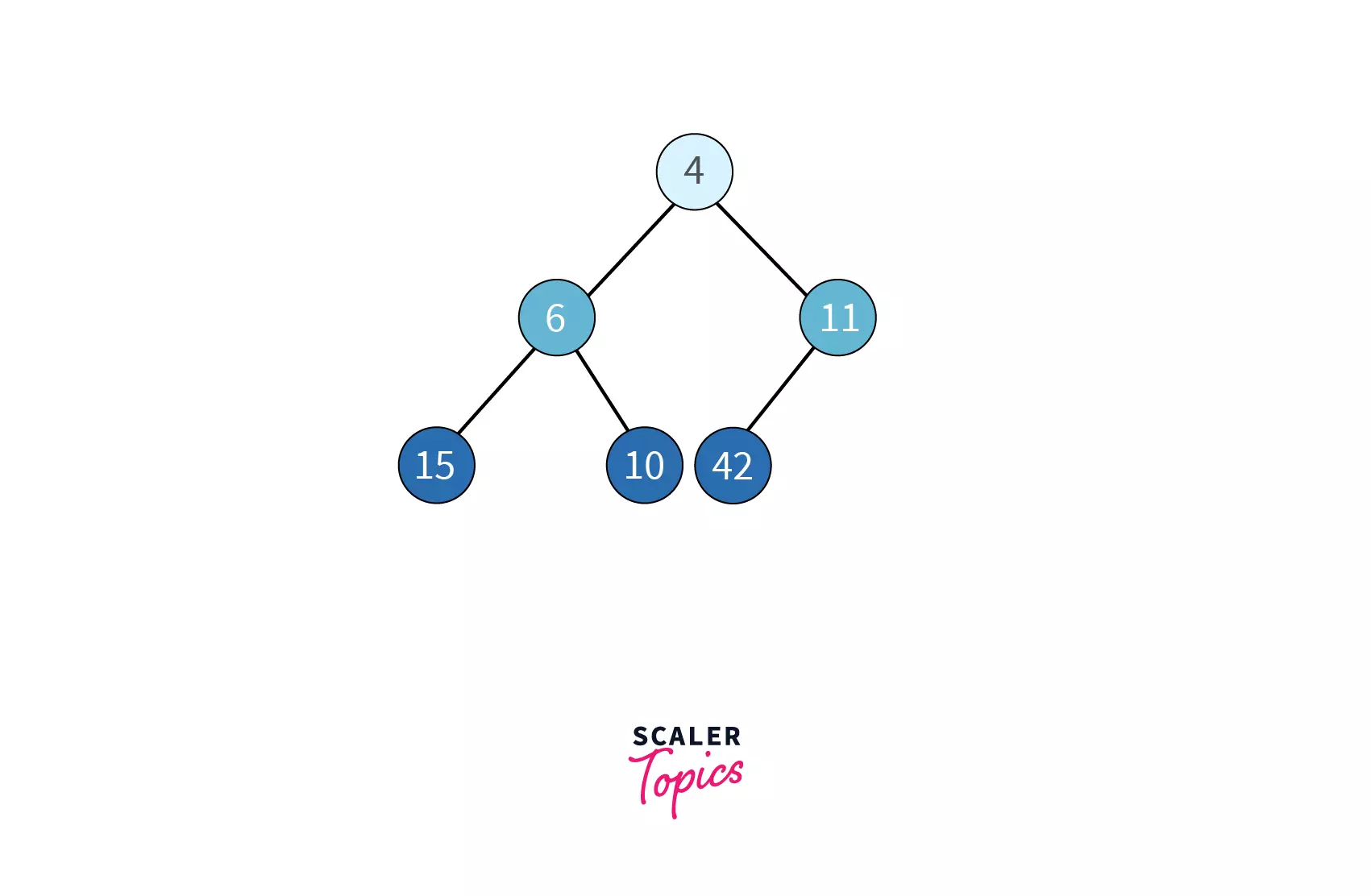
In a min heap, every node’s value is smaller than or equal to both its children.
More Formally:
For a tree to be a max heap it should follow both these conditions:
- The tree should be a complete binary tree (this is the condition for heap).
- Value of each node must be smaller than all its children.
This means that the root of the tree will be the node with a minimum value.
In the following example of the min heap, notice every node is smaller than both its children.
Max Heap
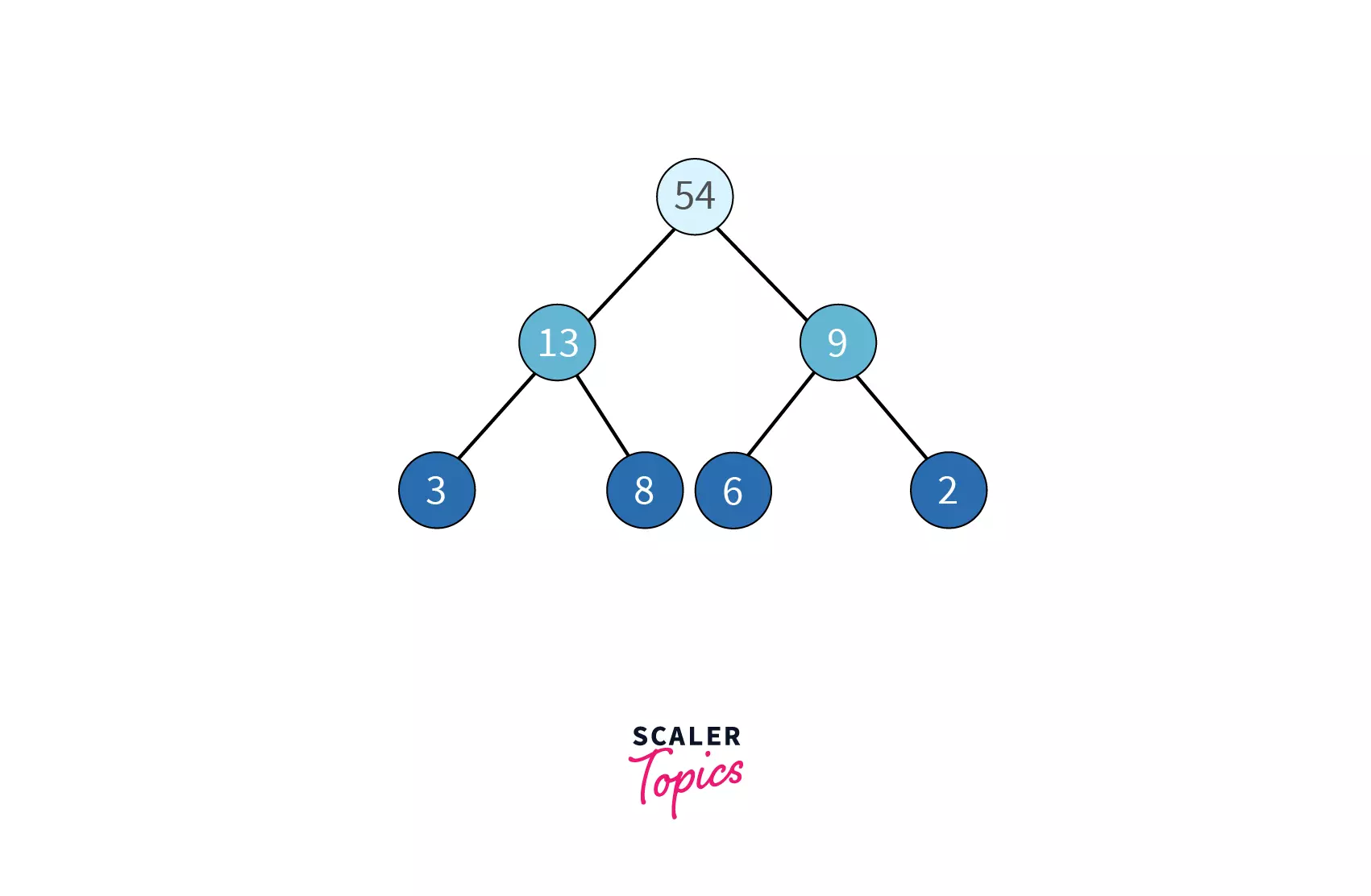
In a Max heap, every node’s value is greater than or equal to both its children. How does this help us? If every parent is greater than its children, which node would have the greatest value? That’s right – the root node. You can directly access the root node to get the maximum element in a max heap.
More Formally:
For a tree to be a max heap it should follow both these conditions:
- The tree should be a complete binary tree (this is the condition for heap)
- Value of each node must be greater than all its children
In the following example of the max heap, notice every node is greater than both its children.
Difference Between Min Heap and Max Heap
| Min Heap | Max Heap |
|---|---|
| In a Min-Heap, the value stored at the root node must be less than or equal to the values stored at each of its children | In a Max-Heap, the value stored at the root node must be greater than or equal to the values stored at each of its children |
| Minimum element in the complete tree is at the root of the tree and can be retrieved in constant time | Maximum element in the complete tree is at the root of the tree and can be retrieved in constant time |
| If used for sorting purposes, Min-Heap sorts elements in ascending order. | If used for sorting purposes, Max-Heap sorts elements in descending order. |
| When constructing a Min-Heap, the smallest element is given the highest priority | When constructing a Max-Heap, the largest element is prioritized. |
Example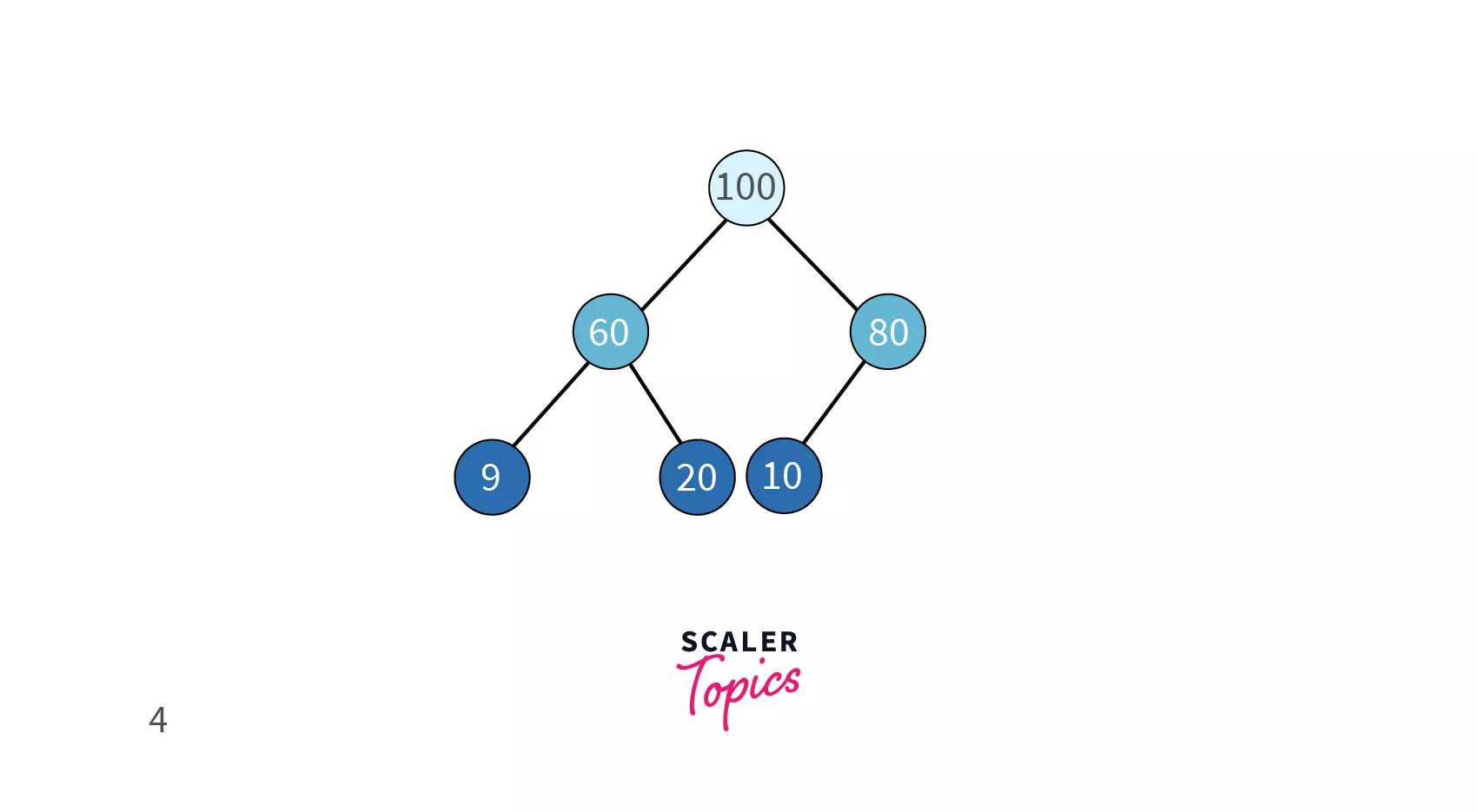 | Example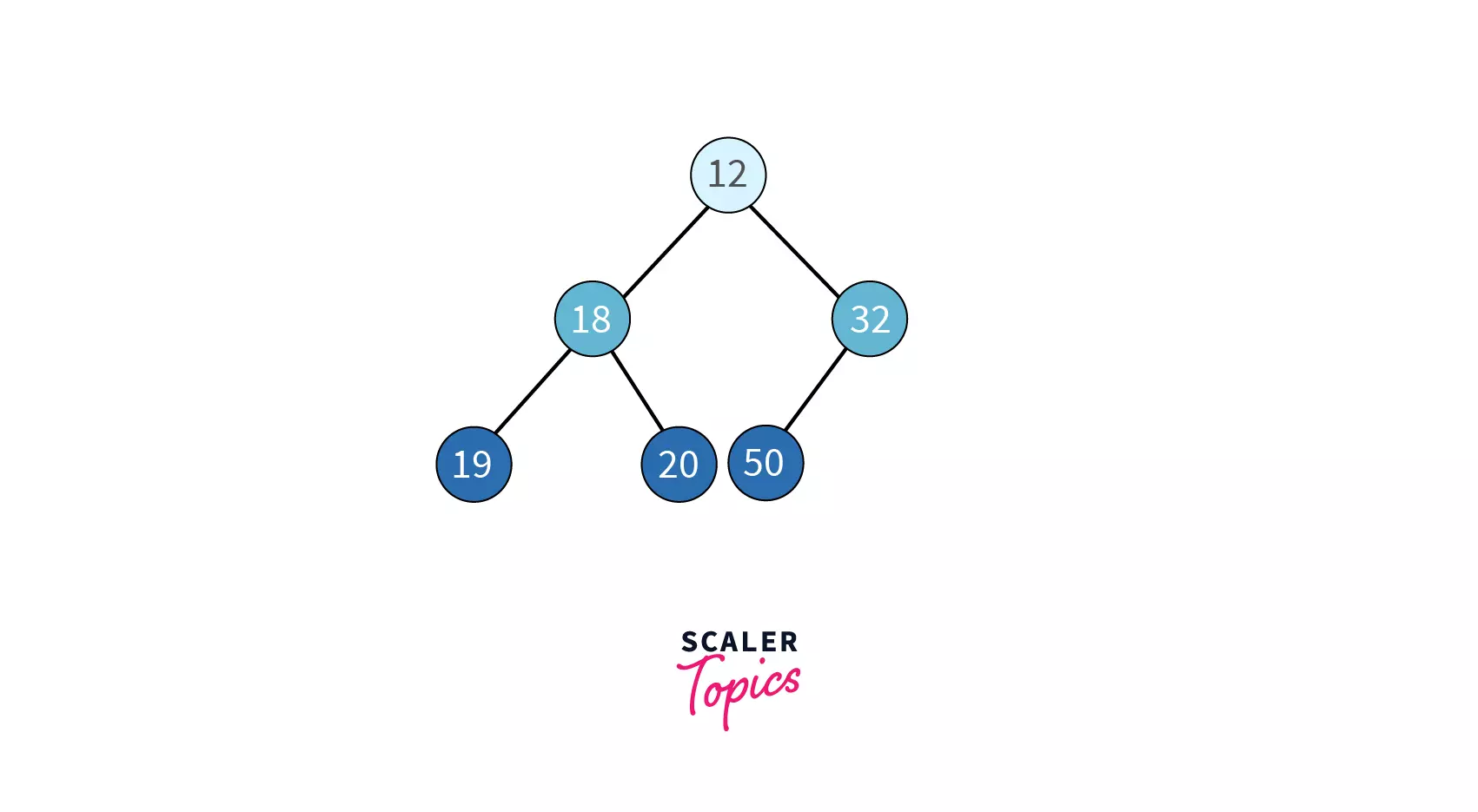 |
Applications of Heap
- Heap Sort: Heap Sort is a sorting algorithm. It has a time complexity of O(N*log N) that leverages the Binary Heap data structure. By organizing data into a heap, it enables fast sorting operations.
- Priority Queue: Priority queue benefit from heap implementation, allowing for swift execution of essential operations such as
insert(), delete(), extractMax(), anddecreaseKey(), all achievable in O(log N) time. - Graph Algorithms: Heaps play a pivotal role in various graph algorithms, including Dijkstra’s Shortest Path and Prim’s Minimum Spanning Tree algorithms. Their efficient structure facilitates optimal path finding and tree construction, enhancing the performance of these algorithms.
- Dynamic Memory Allocation: Heaps are also instrumental in dynamic memory allocation tasks, where they efficiently manage memory blocks based on their priorities or sizes, ensuring optimal memory utilization and management.
- Operating Systems: Heaps are integral to memory management in operating systems, facilitating tasks such as process scheduling, memory allocation, and resource optimization. By efficiently organizing memory blocks, heaps contribute to the smooth operation of various system functions.
Complexity Analysis of Min Heap and Max Heap
Maximum or Minimum Element Retrieval: Achievable in constant time O(1), making it highly efficient for retrieving the extreme values from a heap.
Insertion into Max-Heap or Min-Heap: Inserting an element into a heap, whether it’s a Max-Heap or Min-Heap, requires logarithmic time complexity O(log N), ensuring swift addition of elements while maintaining the heap property.
Removal of Maximum or Minimum Element: Removing the maximum or minimum element from a heap can be done in O(log N), ensuring efficient extraction of extremal values without compromising the heap structure.
Explore Scaler Topics Data Structures Tutorial and enhance your DSA skills with Reading Tracks and Challenges.
Conclusion
- Heaps, whether in the form of Min Heaps or Max Heaps, offer efficient data structuring for various applications due to their complete binary tree organization.
- Min Heap ensures that the smallest element is at the root, facilitating constant-time retrieval of the minimum element.
- Max Heap guarantees the largest element is at the root, allowing for quick access to the maximum value.
- Both Min Heap and Max Heap find extensive use in sorting algorithms like Heap Sort and data structures like Priority Queues, enhancing efficiency through fast operations.
- Graph algorithms such as Dijkstra’s Shortest Path and Prim’s Minimum Spanning Tree benefit significantly from heaps, streamlining pathfinding and tree construction processes.
- Complexity analysis reveals that heaps offer optimal time complexities for key operations like element retrieval, insertion, and removal, ensuring swift processing even with large datasets.