The Difference Between BFS and DFS lies in their traversal methods. BFS explores nodes level by level, making it ideal for finding the shortest path. In contrast, DFS explores, as far as possible, each branch suited for topological sorting and detecting cycles.
What is BFS?
Breadth-First Search (BFS) is a vertex-based algorithm used to find the shortest path between two nodes in a graph. It explores a graph in a breadth-ward motion, prioritizing the shallowest paths. BFS utilizes a queue data structure (FIFO – First In, First Out) to store visited vertices, making it an efficient way to perform level order traversal of a graph. It is also known as level order traversal.
Example
Let’s consider the below graph for the breadth-first search traversal.
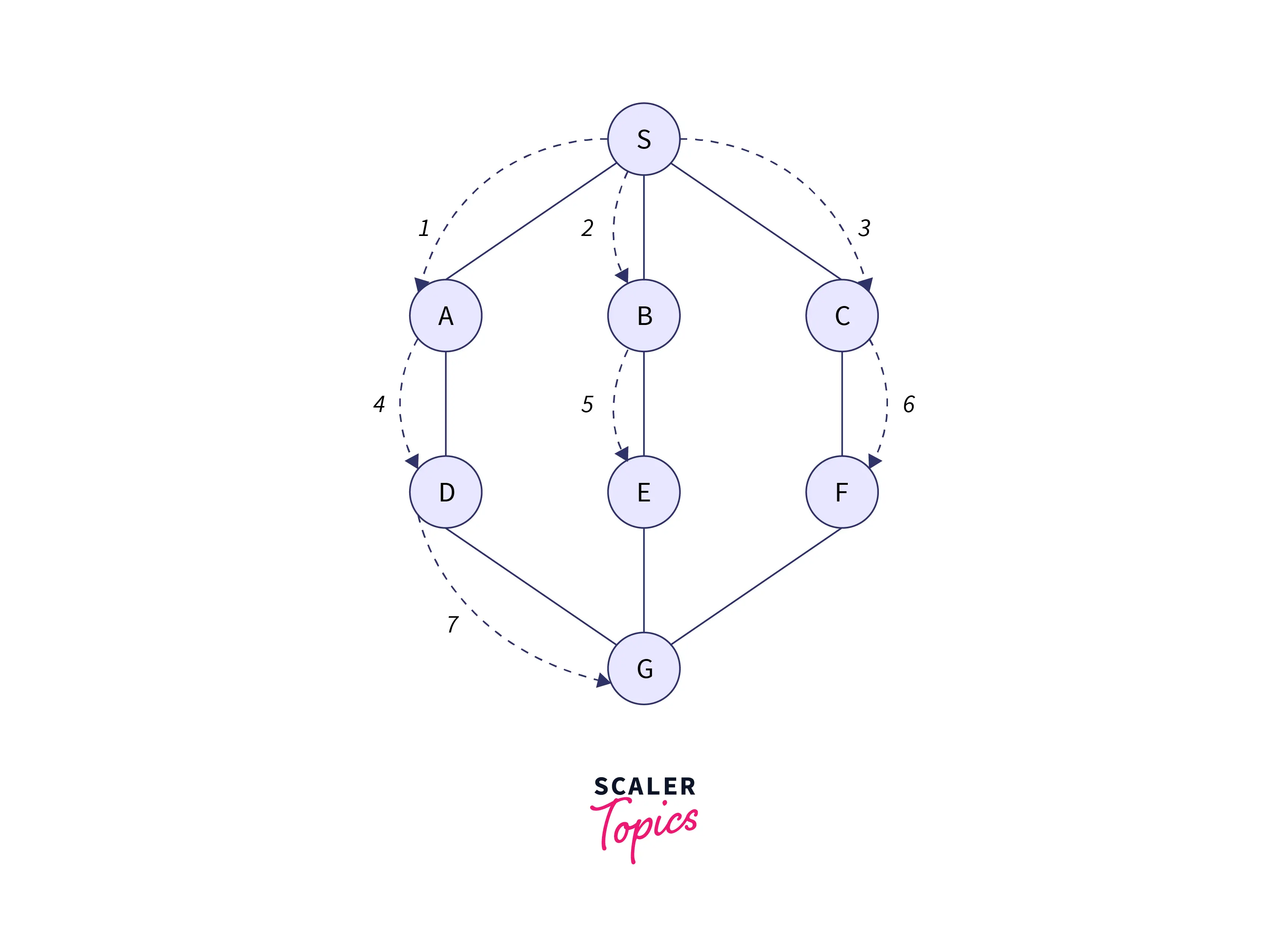
The Final Output we get after BFS for the given graph is:
S A B C D E F G
What is DFS?
DFS(Depth First Search) is an edge-based traversal method that explores vertices recursively, utilizing a stack for storing visited vertices in a LIFO manner. It’s faster and more memory-efficient than BFS. By prioritizing deep unexplored nodes and backtracking as it pops elements from the stack, DFS ensures each vertex is visited exactly once and each edge is checked twice.
Example
Let’s consider the below graph for the depth-first search traversal.
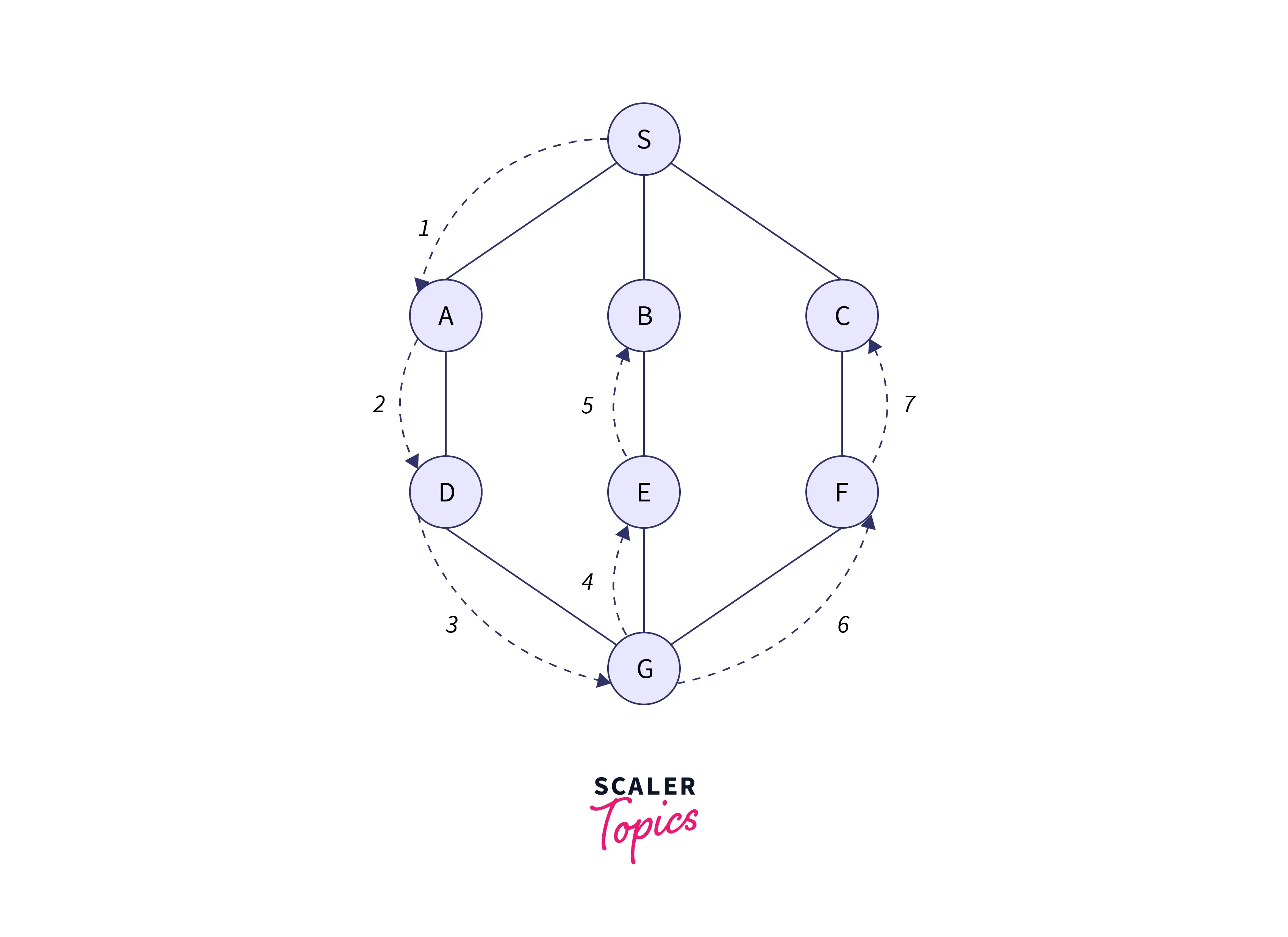
Output:
S A D G E B F C
Differences between BFS and DFS
Below table clearly explains about all the difference between BFS and DFS.
| S.No | BFS | DFS |
|---|---|---|
| 1 | BFS: Breadth First Search. | DFS: Depth First Search. |
| 2. | BFS is better when the destination vertex is closer to the source index. | DFS is better when the destination is far away from the source. |
| 3. | In Breadth First Search, each node is traversed only once. | In Depth First Search, each node is traversed twice due to backtracking. |
| 4. | You can use BFS to find a single source of the shortest path in the case of an unweighted graph. It is because, in BFS, one can easily reach the vertex with a minimum number of edges from the source vertex. | In DFS, it might need to traverse through more edges than BFS to find and reach the destination vertex from your source vertex. |
| 5. | The amount of memory required for BFS is more than that of DFS. | The amount of memory required for DFS is less than that of BFS. |
| 6. | Time Complexity of BFS = O(V+E) where V is the number of vertices and E is the number of edges in the given graph. | Time Complexity of DFS = O(V+E) where V is the number of vertices and E is the number of edges in the given graph. |
| 7. | BFS constructs the tree in a level-wise manner. | DFS constructs the tree one sub-tree at a time. |
| 8. | BFS finds utility in applications like identifying bipartite graphs and calculating shortest paths. | DFS is commonly used for tasks such as exploring acyclic graphs and determining topological orders. |
| 9. | BFS doesn’t encounter problems with infinite loops. | DFS may lead to situations where the algorithm gets stuck in an infinite loop. |
| 10. | BFS is a vertex-based algorithm | DFS is an edge-based algorithm |
| 11. | Queue data structure is used in BFS. | DFS uses stack or recursion |
| 12. | BFS is unsuitable for game decision-making trees | DFS is preferred for such scenarios |
| 13. | BFS visits siblings before children | DFS visits children before siblings |
| 14. | BFS is slower | DFS is faster than BFS |
Explore Scaler Topics Data Structures Tutorial and enhance your DSA skills with Reading Tracks and Challenges.
Conclusion
- DFS and BFS are graph traversal techniques with the same time complexity but differing space consumption.
- DFS typically requires less space as it remembers only a single path with unexplored nodes, whereas BFS stores every node in memory, consuming more space.
- DFS yields deeper solutions and is generally not considered optimal, although it can be optimal in dense graphs.
- BFS is considered more efficient as it searches for the optimal goal first, making it suitable for specific scenarios.