Deletion in BST

The delete function in a binary search tree removes a specified node, ensuring the binary search tree property is maintained. Three scenarios govern node deletion. This article explores the process of deleting nodes in a binary tree while introducing the fundamentals of what a binary search tree entails.

To learn more about the Binary search tree. click here

Deletion in Binary Search Tree

A binary search tree’s given node can be removed using the delete function. However, we have to remove a node from a binary search tree in a way that doesn’t break that property(A node’s right subtree only contains nodes with keys higher than the node’s key, and its left subtree only contains nodes with keys lower than the node’s key. A binary search tree must also be present in both the left and right subtrees.). There are three instances of deleting a node from a binary search tree.

The Node to be Deleted in Binary Search Tree is a Leaf Node

This is the simplest scenario. Simply replace the leaf node with NULL/None and release the space that has been allotted.

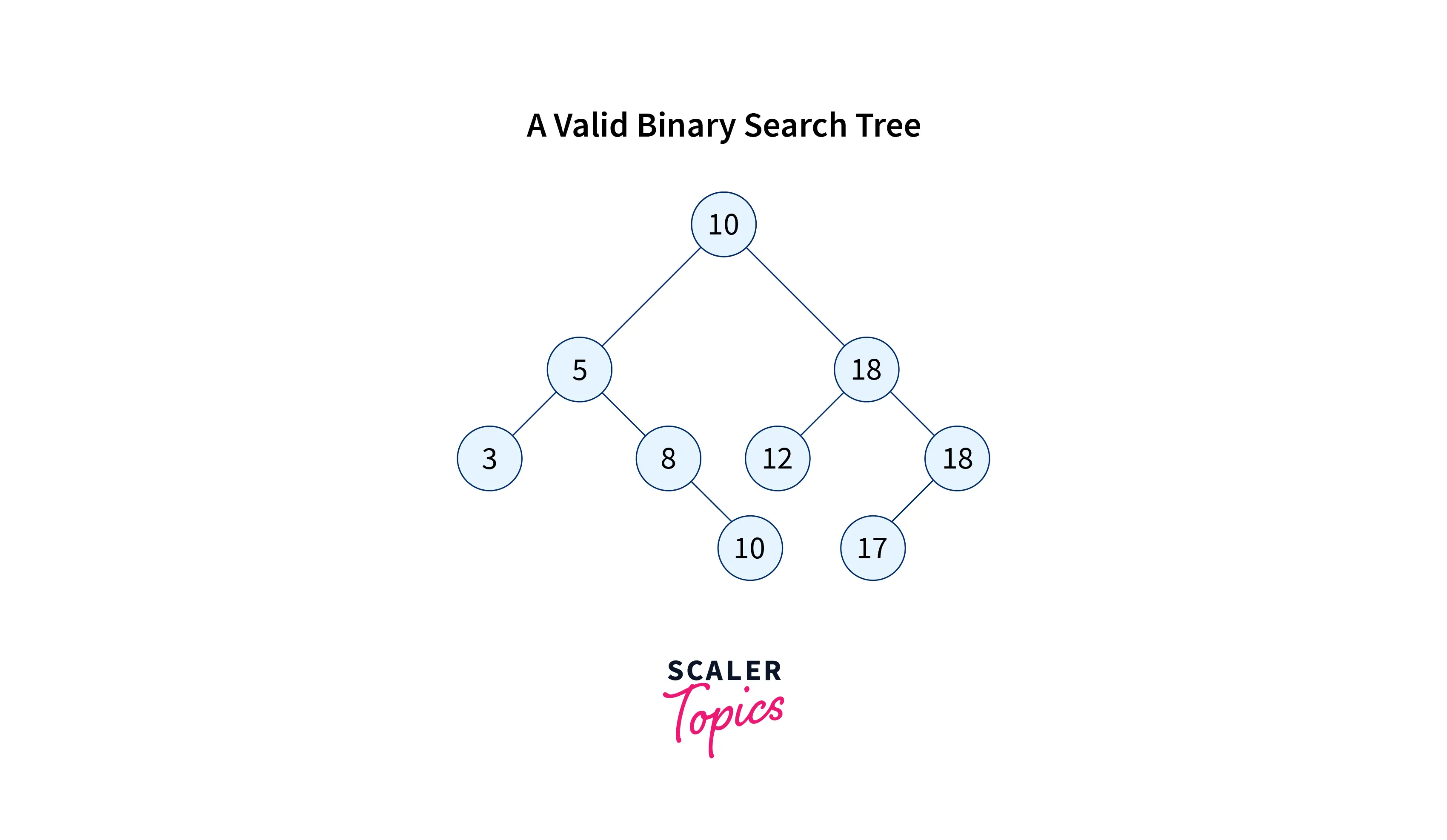
In the Above BST if we want to delete 17 we will replace this with None/Null.

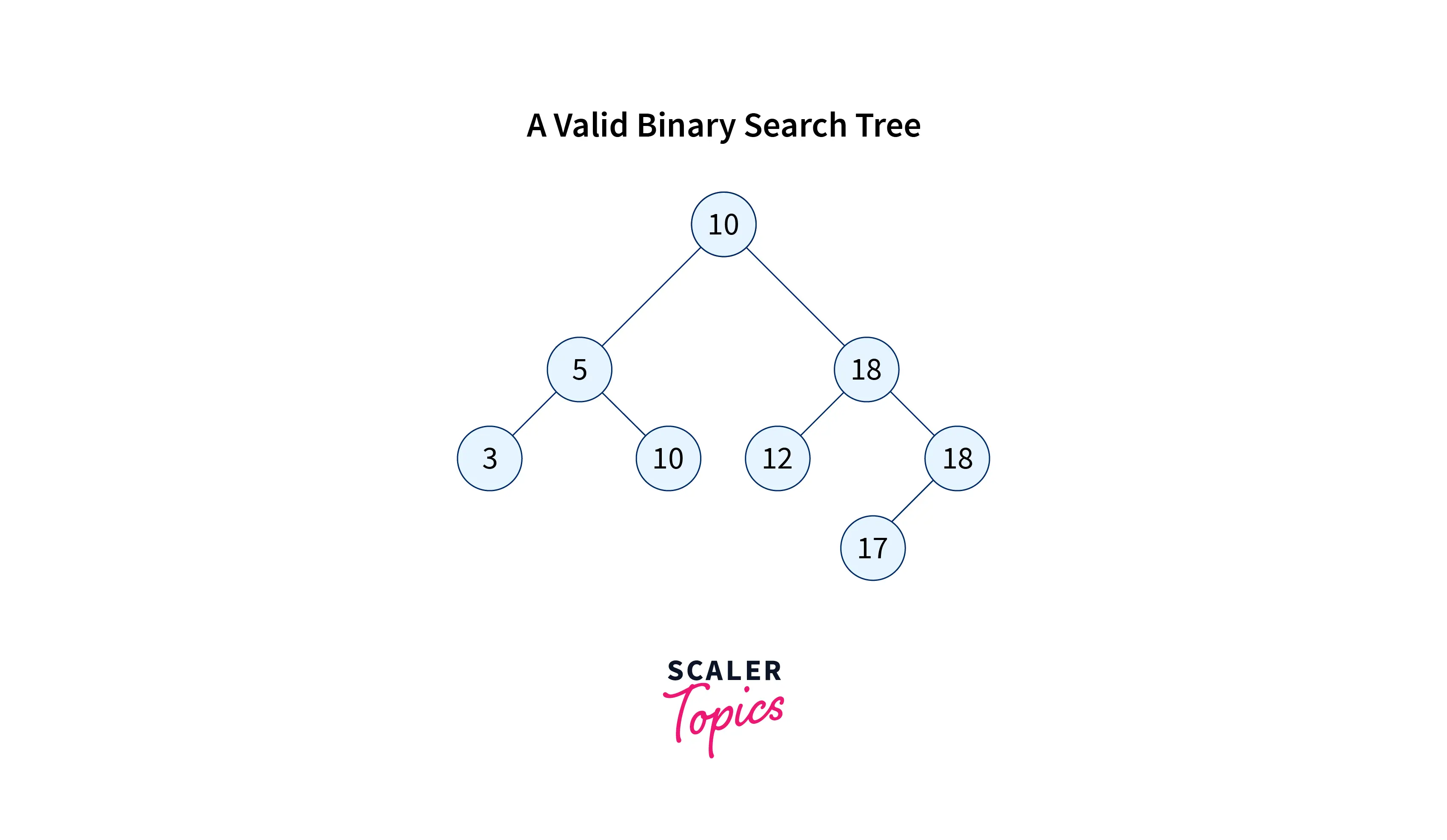
The Node to be Deleted in Binary Search Tree has Only One Child

Replace the node in this instance with its child and then remove the child node because it now has the value that needs to be destroyed. Simply replace it with NULL to release the space that was allotted.

In the above BST if we want to delete 8 then we replace it with 10 and remove 10 or copy 10to the 8 and remove 10.

The Node to be Deleted in Binary Search Tree has Two Children

Compared to the previous two situations, it is a little more complicated. However, until the node value (to be deleted) is placed on the leaf of the tree, the node that is to be removed is replaced by its in-order successor or predecessor recursively.

Inorder Successor :
The following node in the Binary Tree’s Inorder traversal is referred to as a node’s Inorder successor. For the final node in an inorder traverse, Inorder Successor is NULL.

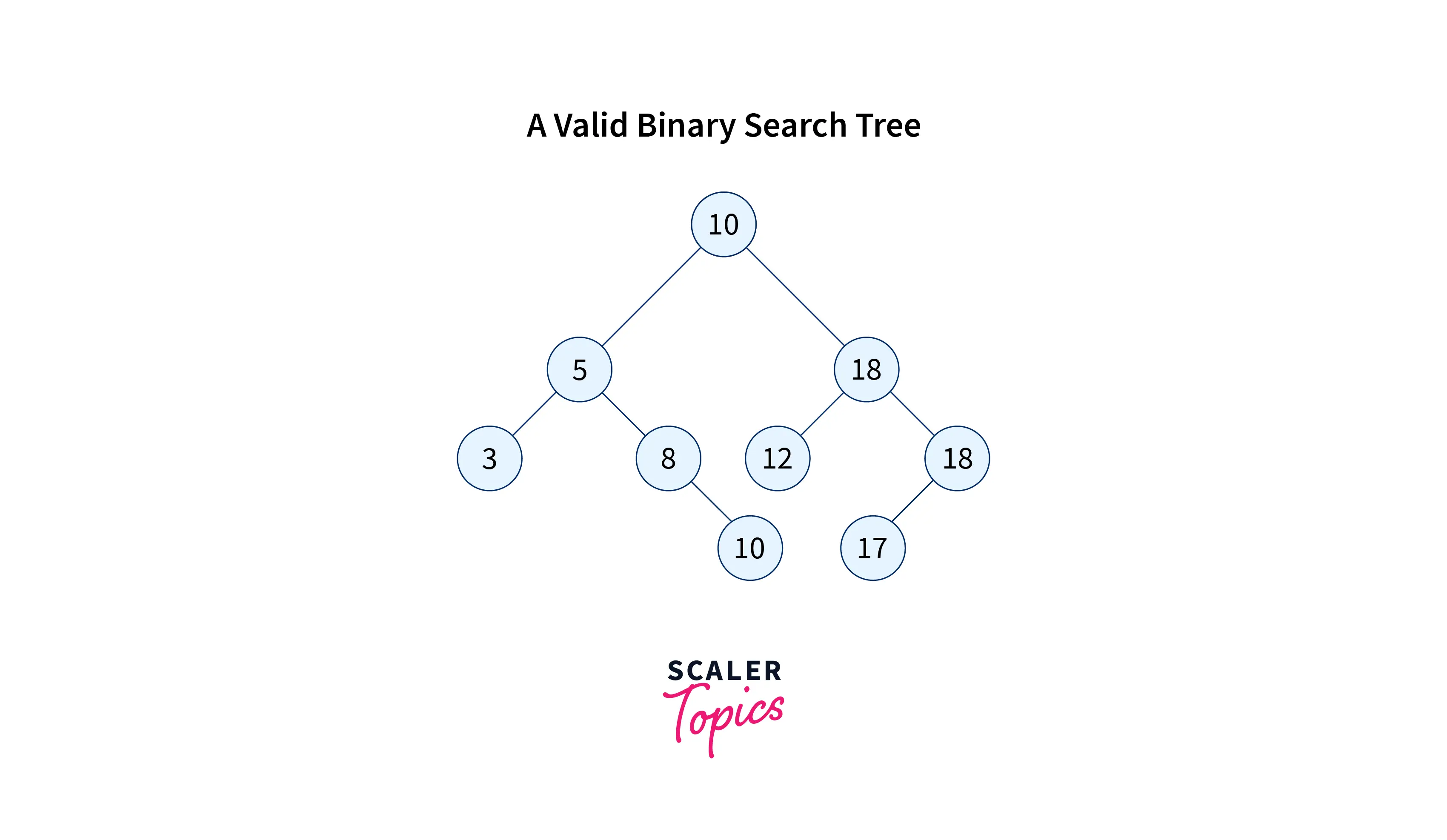
In the above BST if we want to remove 5 then first we will find an inorder successor(To get a node which is just greater than the node to be deleted) so the inorder successor is 8 so we replace 5(node to be deleted) with 8(inorder successor) and delete 8.

Example

Problem Statement

Given a binary search tree and a key value. The task is to delete

Algorithm

Step – 1 :
if root is null then return null.
Step – 2 :
if root.key < key then find the node in right subtree root.right=delNode(root.right.key).
Step – 3 :
if root.key > key then find the node in left subtree root.right=delNode(root.right.key).
Step – 4 :
if root.key==key

• if root.left == null and root.right == null then return null
• if root.left==null return root.right
• if root.right=null return root.left
• if root.left!=null and root.right!=null then find inorder successor or predecessor and replace it with the root node and delete inorder successor or predecessor.

Code

Python :

# Node class
class Node:
    def __init__(self, value) -> None:
        self.left = None
        self.right = None
        self.value = value

# get the inorder successor of node

def inorder_successor(node):
# 	inorder successor of node
    node = node.right
    while(node != None and node.left != None):
        node = node.left
        print(node, "value of node is")
    return node


def delNode(root, node):
# 	if the root is none then return
    if root is None:
        return root
# if the node to be deleted is at the right subtree
    if root.value < node.value:
        root.right = delNode(root.right, node)
# if node to be deleted is at left subtree
    elif root.value > node.value:
        root.left = delNode(root.left, node)
    else:
# 		if node is leaf node then simply return None
        if root.left == None and root.right == None:
            return None
# if node has only one child either at left or right then return that
        if root.left == None:
            return root.right
        if root.right == None:
            return root.left
# if node has two child
        else:
# 		find inorder successor of child
            successor = inorder_successor(root)
# 	copy inorder successor data to node
            root.value = successor.value
# and delete successor
            root.right = delNode(root.right, successor)
    return root


root = Node(10)
root.left = Node(5)
root.right = Node(15)
root.left.left = Node(3)
root.left.right = Node(7)
root.right.left = Node(13)
root.right.right = Node(17)
print(delNode(root, root.left))
print(root.left.value)

Java :

/**
 * DeletionBST
 */
public class DeletionBST {

  public static Node delNode(Node root, Node node) {
    // 		if root is null(when node not found)
    if (root == null) {
      return root;
    }
    // if node to be deleted is in right subtree
    if (root.value < node.value) {
      // 			delNode will return right subtree after deleting node
      root.right = delNode(root.right, node);
    }
    // 		if node is in left subtree
    else if (root.value > node.value) {
      // 			delNode will return left subtree after deleting node
      root.left = delNode(root.left, node);
    } else {
      // 			when node is leaf node then return null
      if (root.left == null && root.right == null) {
        return null;
      }
      // 			when node has one child
      if (root.left == null) {
        return root.right;
      }
      if (root.right == null) {
        return root.left;
      }
      // 			when node has two child
      else {
        // we are finding inorder successor and replace it with node and removing successor
        Node successor = inorder_successor(root);
        root.value = successor.value;
        root.right = delNode(root.right, successor);
      }
    }
    return root;
  }

  public static Node inorder_successor(Node node) {
    // 		to get inordersuccessor simply find
    // 		extreme left of right subtree of node
    node = node.right;
    while (node != null && node.left != null) node = node.left;
    return node;
  }

  public static void main(String[] args) {
    Node root = new Node(10);
    root.left = new Node(5);
    root.right = new Node(15);
    root.left.left = new Node(3);
    root.left.right = new Node(7);
    root.right.left = new Node(13);
    root.right.right = new Node(17);
    delNode(root, root.left);
    System.out.println(root.left.value);
  }
}

class Node {
  Node left, right;
  int value;

  Node(int val) {
    left = null;
    right = null;
    this.value = val;
  }
}

CPP :

#include <bits/stdc++.h>
using namespace std;

// structure for node
struct Node
{
  int key;
  struct Node *left;
  struct Node *right;
  Node(int k){
      key=k;
      left=right=NULL;
  }
};

Node *getSuccessor(Node *curr){
// 		to get inordersuccessor simply find
// 		extreme left of right subtree of node
    curr=curr->right;
    while(curr!=NULL && curr->left!=NULL)
        curr=curr->left;
    return curr;
}

Node *delNode(Node *root, int x){
// 	if root is null(when node is not fouund)
    if(root==NULL)
        return root;
// 	if node is in left subtree
    if(root->key>x)
        root->left=delNode(root->left,x);
// 	if node is in right subtree
    else if(root->key<x)
        root->right=delNode(root->right,x);
    else{
// 		if left child is null then return right child in case both are null then it will return right child(null)

        if(root->left==NULL){
            Node *temp=root->right;
            delete root;
            return temp;
        }
// 		if left is not null and right is null then it will return right child
        else if(root->right==NULL){
            Node *temp=root->left;
            delete root;
            return temp;
        }
// 		when node has two child then find inorder successor and replace it with node and delete inorder successor
        else{
            Node *succ=getSuccessor(root);
            root->key=succ->key;
            root->right=delNode(root->right,succ->key);
        }
    }
    return root;
}

void inorder(Node *root){
    if(root!=NULL){
        inorder(root->left);
        cout<<root->key<<" ";
        inorder(root->right);
    }
}
int main() {

	Node *root=new Node(10);
	root->left=new Node(5);
	root->right=new Node(15);
    root->left->left=new Node(3);
    root->left->right=new Node(7);
	root->right->left=new Node(13);
	root->right->right=new Node(17);
	int x=15;

	root=delNode(root,x);
	inorder(root);
}

Complexity

Time Complexity :
$O(logN)$, N = the number of nodes.
Due to the fact that the given tree is a BST, we need to traverse either the right subtree or the left subtree at any given point. Therefore, $log(N)$ is the time complexity.

Space Complexity :
For a recursion stack, the space complexity is $O(H)$, where H is the BST’s height

Conclusion

• In a Binary search tree, the value of left node must be smaller than the parent node, and the value of right node must be greater than the parent node.
• A binary search tree’s given node can be removed using the delete function. However, we have to remove a node from a binary search tree in a way that doesn’t break that property(the left node should be less than the parent and the right node should be greater than the parent)
• To delete a node in BST there will be three possibility

1. The node to be deleted is a leaf node : Delete the node and replace it with Null/None
2. The node to be deleted has only one child : Delete the node and replace it with a child
3. The node to be deleted has two children : find inorder successor of the node then copy successor data to the node and delete successor